Книга: Извечные тайны неба
Параллели и меридианы
| <<< Назад Navigare necesse est |
Вперед >>> У каждого свое время |
Разделы на этой странице:
- Высота полюса мира над горизонтом h равна широте места наблюдений ф. Эта легко доказываемая геометрическая теорема с глубокой древности легла в основу методов определения географической широты
- Принцип определения радиуса Земли. Коэффициент ? в формуле служит для перехода от градусной меры к радианной.Поскольку древние ученые для определения радиуса Земли, как правило, прибегали к измерениям дуги меридиана в 1 градус, за подобными работами укрепилось общее название градусных измерений
Параллели и меридианы
В IV в. до н. э. величайший мыслитель древности Аристотель доказал, что наша планета имеет форму, очень близкую к форме шара.
Примерно в то же время, наблюдая во время путешествий в различных местах видимое движение звезд и Солнца, древние ученые установили для ориентировки на земной поверхности определенные условные линии.
Отправимся в мысленное путешествие по поверхности Земли. Положение над горизонтом воображаемой оси мира, вокруг которой происходит суточное вращение небесного свода, будет для нас все время меняться. В соответствии с этим будет меняться и картина движения звездного неба.
Поехав на север, мы увидим, что звезды в южной части неба поднимаются каждую ночь на меньшую высоту. А звезды в северной части – в нижней кульминации – имеют большую высоту. Двигаясь достаточно долго, мы попадем на Северный полюс. Здесь вообще ни одна звезда не поднимается и не опускается. Нам будет казаться, что все небо медленно кружится параллельно горизонту.
Древние путешественники не знали, что видимое движение звезд является отражением вращения Земли. И они не бывали на полюсе. Но им необходимо было иметь ориентир на земной поверхности. И они выбрали для этой цели легко определяемую по звездам линию север – юг. Эта линия получила название меридиана.
Меридианы можно проводить через любые точки на поверхности Земли. Множество меридианов образует систему воображаемых линий, соединяющих Северный и Южный полюсы Земли, которые удобно использовать для определения местоположения.
Примем один из меридианов за начальный. Положение любого другого меридиана в этом случае будет известно, если указано направление отсчета и задан двугранный угол между плоскостью искомого меридиана и плоскостью начального (нулевого) меридиана.
Положение нулевого меридиана на протяжении веков многократно менялось. В 1493 г., сразу же после первого плавания Колумба к берегам Вест-Индии, папа римский Александр VI поделил подлунный мир между Испанией и Португалией. Граница грядущих владений двух величайших морских держав рассекала Атлантический океан от полюса до полюса. И когда спустя десятилетия выяснились контуры земель Нового Света и далекие рубежи Азии, оказалось, что в западную, «испанскую» половину земного шара попала вся Америка, за исключением лишь ее бразильского выступа, а в восточную, «португальскую» половину угодили, помимо Бразилии, целиком Африка и Азия.
Такая линия отсчета долгот просуществовала около ста пятидесяти лет. В 1634 г. при кардинале Ришелье специальная комиссия французских эрудитов предложила провести нулевой меридиан ближе к Европе, но таким образом, чтобы вся территория Европы и Африки оказалась к востоку от него. Для этой цели нулевой меридиан провели через самую западную точку Старого Света – западную оконечность самого западного из архипелага Канарских островов – остров Ферро. В 1884 г. на астрономической конференции в Вашингтоне за начальный, отсчетный меридиан для земного шара был принят тот, который проходит через ось одного из телескопов Гринвичской обсерватории. Гринвичский меридиан в качестве нулевого сохраняется и поныне.
Угол, образованный каким-либо меридианом с начальным, называют долготой. Долгота, например, меридиана Москвы – 37° к востоку от Гринвича.
Чтобы отличить друг от друга точки, лежащие на одном и том же меридиане, пришлось ввести вторую географическую координату – широту. Широтой называют угол, который проведенная в данном месте поверхности Земли отвесная линия образует с плоскостью экватора.
Термины «долгота» и «широта» дошли до нас от древних мореходов, которые описывали длину и ширину Средиземного моря. Та координата, которая соответствовала измерениям длины Средиземного моря, стала долготой, а та, которая соответствовала ширине, стала современной широтой.
Нахождение широты, как и определение направления меридиана, тесно связано с движением звезд. Уже древние астрономы доказали, что высота полюса мира над горизонтом h в точности равна широте места ?.
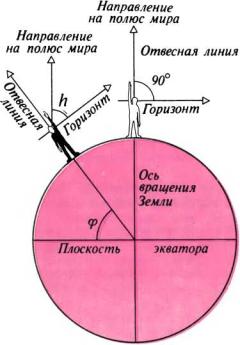
Высота полюса мира над горизонтом h равна широте места наблюдений ф. Эта легко доказываемая геометрическая теорема с глубокой древности легла в основу методов определения географической широты
Предположим, что Земля имеет форму правильного шара, и рассечем ее по одному из меридианов, как показано на рисунке. Пусть на Северном полюсе стоит человек, изображенный на рисунке в виде светлой фигуры. Для него направление вверх, т. е. направление отвесной линии, совпадает с осью мира. Полюс мира находится у него прямо над головой. Высота полюса мира равна здесь 90°.
Так как видимое вращение звезд вокруг оси мира является отражением реального вращения Земли, то в любой точке Земли, как мы уже знаем, направление оси мира остается параллельным направлению оси вращения Земли. Направление же отвесной линии при переходе из точки в точку меняется.
Возьмем, например, другого человека (на рисунке темная фигура). Направление оси мира у него осталось таким же, как у первого. А направление отвесной линии изменилось. Поэтому высота полюса мира над горизонтом здесь не 90°, а значительно меньше.
Из простых геометрических соображений ясно, что высота полюса мира над горизонтом (на рисунке угол h) действительно равна широте (угол ?).
Линия, соединяющая точки с одинаковыми широтами, получила название параллели.
Меридианы и параллели образуют так называемую систему географических координат. Каждая точка на земной поверхности имеет вполне определенную долготу и широту. И наоборот, если известна широта и долгота, то можно построить одну параллель и один меридиан, в пересечении которых получится одна-единственная точка.
Понимание особенностей суточного движения звезд и введение системы географических координат позволили осуществить первое определение радиуса Земли. Оно было выполнено во второй половине III в. до н. э. известным математиком и географом Эратосфеном.
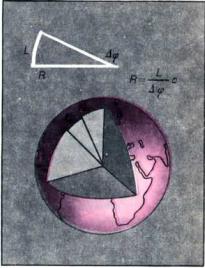
Принцип определения радиуса Земли. Коэффициент ? в формуле служит для перехода от градусной меры к радианной.
Поскольку древние ученые для определения радиуса Земли, как правило, прибегали к измерениям дуги меридиана в 1 градус, за подобными работами укрепилось общее название градусных измерений
Принцип этого определения заключается в следующем. Пусть удалось измерить разность широт двух точек, лежащих на одном меридиане (см. рис.). Тем самым нам стал известен угол ?? с вершиной в центре Земли, который соответствует дуге меридиана L на поверхности Земли. Если теперь удастся измерить также и дугу L, то мы получим сектор с известной длиной дуги и соответствующим ей центральным углом. На рисунке этот сектор показан отдельно. Путем несложных вычислений можно получить величину радиуса этого сектора, который и является радиусом Земли.
Эратосфен, грек по национальности, жил в богатом египетском городе Александрии. Он был человеком разносторонне образованным, его увлекали подчас очень далекие друг от друга области науки. Друзья в шутку прозвали Эратосфена на спортивный манер «пятиборцем»: его не смущали трудности и, словно спортсмен, принимающий участие в пяти разных видах соревнований, Эратосфен для решения интересующей его задачи всегда готов был ринуться в любую новую область знаний.
К югу от Александрии находился другой город – Сиена, который в наши дни называется Асуаном и где, как известно, с помощью Советского Союза сооружена знаменитая высотная плотина. Эратосфен знал, что Сиена обладает интересной особенностью. В полдень одного из июньских дней Солнце над Сиеной бывает настолько высоко, что его отражение видно на дне даже очень глубоких колодцев. Отсюда Эратосфен заключил, что высота Солнца в Сиене в этот день равна точно 90°. Кроме того, раз Сиена лежит строго к югу от Александрии, то они находятся на одном меридиане.
Для необычного измерения Эратосфен решил воспользоваться скафисом – чашеобразными солнечными часами со штырьком и делениями внутри них. Установленные вертикально, эти солнечные часы по тени от штырька дают возможность измерить высоту Солнца над горизонтом. И в полдень того самого дня, когда Солнце над Сиеной поднялось настолько высоко, что все предметы перестали отбрасывать тени, Эратосфен измерил его высоту на городской площади Александрии.
Солнце в Александрии, по измерениям Эратосфена, отстояло от зенита на 1/50 часть окружности. Стало быть, разность широт Александрии и Сиены в градусной мере составляет 7°12?.
Оставалось измерить расстояние между ними. Но как это сделать? Как измерить на поверхности Земли расстояние, равное в современных единицах примерно 800 км?
Трудности подобного предприятия были тогда буквально неисчислимы. Действительно, как изготовить такую гигантскую линейку, с помощью которой можно было бы произвести измерения? Как сделать, чтобы на протяжении 800 км эта линейка укладывалась строго по меридиану без всяких перекосов?
Но Эратрсфен недаром был выдающимся ученым. Его измерения высот Солнца отличались завидной точностью. Это легко проверить, поскольку он выполнял различные измерения. Так, например, он получил разность высот Солнца в одном и том же месте в день летнего и зимнего солнцестояний, равную 11/83 частей круга, т. е. 47°43?; эта величина равна удвоенному углу между небесным экватором и эклиптикой и, как нетрудно убедиться по современным справочникам, получена с очень небольшой погрешностью. Предусмотрел Эратосфен и необходимость как можно более точно знать расстояние между Александрией и Сиеной.
Александрия и Сиена лежат в плодородной долине Нила, там, где исстари искусные шагатели-бематисты проводили тщательное межевание земель. Там же из года в год вереница за вереницей двигались навстречу друг другу торговые караваны. Расстояние между Александрией и Сиеной было известно в эпоху Эратосфена, пожалуй, гораздо более точно, чем расстояние между любыми другими отдаленными пунктами античного мира: оно составляло 5 тыс. греческих стадиев. Эратосфен принял это расстояние за истинное и, использовав его, вычислил радиус Земли.
Какова длина греческого стадия в современных мерах? Этот вопрос до сих пор вызывает множество неясностей и кривотолков. Чтобы ответить на него, пришлось проштудировать все географические книги древних, в которых упоминаются расстояния одновременно и в греческих стадиях, и в хорошо известных нам римских милях. Неожиданную помощь оказали сохранившиеся армянские книги по географии VII в.; описанная в них система мер, как в зеркале, отразила систему мер античности. В результате всех изысканий было установлено, что длина стадия Эратосфена близка к 158,5 м.
Если сравнить найденную Эратосфеном величину радиуса Земли с современными данными, то получится, что он ошибся очень немного, меньше чем на 100 км. Этот результат оставался непревзойденным по точности вплоть до XVII в.
Так, с III в. до н. э., со времени Эратосфена, переплелись пути астрономии и геодезии – другой древней науки, изучающей форму и размеры как всей Земли в целом, так и отдельных ее частей.
Методы астрономических определений широт развивались и совершенствовались. Это было особенно важно, в частности, именно в связи с необходимостью более тщательного определения размера Земли. Ибо, начиная с того же Эратосфена, было уяснено, что задача определения размера Земли распадается на две части: астрономическую, т. е. определение разности широт, и геодезическую, т. е. определение длины дуги меридиана. Эратосфен сумел решить астрономическую часть задачи, и принципиально тем же путем шли многочисленные его последователи.
Мы еще будем иметь случай рассказать о более точных измерениях размера Земли, а пока, освоившись с определением широт, займемся делом значительно более сложным – определением географических долгот.
| <<< Назад Navigare necesse est |
Вперед >>> У каждого свое время |
- Не начало, а конец
- Род человеческий
- Спор о начале науки
- Наследие Вавилона
- Не только древний восток
- Navigare necesse est
- Параллели и меридианы
- У каждого свое время
- День за днем
- Неведение Колумба
- Время везут в карете
- Год по Луне и год по Солнцу
- У истоков современных календарей
- Григорианский календарь и наша эра
- Небесные знаки
- Образы далекого прошлого
- Эпоха эллинизма
- Астрономия стран ислама
- Великий Коперник
- Научные истины
- Законодатель неба
- Астрономы вооружаются телескопами
- Признание потомков
- Закон всемирного тяготения
- Механика небес
- От телескопов-карликов к телескопам-гигантам
- Спектральный анализ
- Что не под силу одному…
- Фундамент астрономии
- На Пулковском холме
- Как не сделать из мухи слона
