Книга: Азбука рисунков природы

Каждый охотник желает знать

Каждый охотник желает знать

Из множества природных вариантов мы рассмотрели всего две схемы возникновения рисунков. В первой элементы появляются в точке касания потенциального рельефа пороговым, после чего в примыкающей области происходит разгрузка потенциала, и появление других элементов здесь исключается. Во втором варианте понятием порога мы не оперировали, а первоначальное появление линейных элементов задавалось. Развивались эти элементы в соответствии с потенциальным полем, разгружая его вокруг себя. Теперь рассмотрим вариант, когда элемент появляется при условии Е = Р, но разгрузка происходит лишь в точке касания, т. е. как только где-то выполняется условие Е = Р, тут же скачком в этой точке потенциальный рельеф обрушивается до нулевого уровня. Допустим, пороговый и потенциальный рельефы горизонтальны. В этом случае, как только выполнится условие Е = Р, на всем пространстве произойдет обрушение рельефа — разгрузка потенциала. Наше пространство можно раскрасить в зависимости от значений потенциала. Допустим, при E = 0 пространство белое, а при Е ? Р оно плавно темнеет. Тогда только что описанный процесс будет выглядеть так: все пространство становится темнее и темнее, а затем разом белеет. Пространственной структуры не возникает. Если процесс наращивания потенциала задать непрерывным, то сразу после обрушения потенциальный рельеф вновь начнет воздыматься и через какое-то время опять выполнится условие Е = Р — система будет находиться в колебательном режиме — чем выше скорость наращивания потенциала, тем выше частота колебаний.

Теперь зададим неоднородные условия — выпуклый потенциальный рельеф, например в виде конуса (чем ближе к вершине, тем темнее). В этом случае разгрузка потенциала произойдет в его вершине — здесь образуется кратер (белое пятно), а затем при дальнейшем воздымании и расширении этого поднятия область разгрузки (пятно) будет расширяться. Чем положе рельеф и чем быстрее он воздымается, тем выше скорость расширения. Одновременно с этим в разгруженной части пространства значения потенциала вновь будут наращиваться (центр пятна вновь начнет темнеть), и в какой-то момент в центре рассматриваемой области опять выполнится условие Е = Р и т. д. В итоге возникнет структура из параллельных непрерывно расходящихся контрастных колец. Чем круче наклон первичного потенциального рельефа, тем меньше будет расстояние между кольцами. На рис. 134 показана динамика развития этой структуры в одномерном варианте (в разрезе).

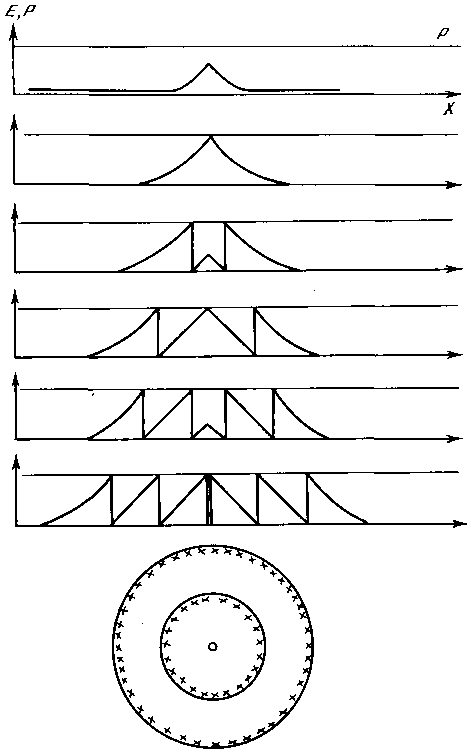
Рис. 134

Подобный механизм можно проиллюстрировать известным явлением возникновения структур при ветровом повале леса. В районах с частым повторением сильных ветров деревья, как только они достигнут определенной высоты, не выдерживают их напора. Такие леса развиваются в колебательном режиме — после ветроповала лес восстанавливается и, достигнув критической высоты, вновь гибнет. Если же условия произрастания деревьев неоднородны в пространстве, то лесной массив состоит из разновозрастных медленно смещающихся полос зеленых деревьев, разделенных бурыми полосами бурелома.

Близкий пример — образование расходящихся волн лишайников на камне. Пятно лишайника разрастается. Со временем его центральная (старая) часть отмирает и образуется расширяющееся кольцо, затем в его центре возникает новое пятно лишайника и т. д. По этой же схеме возникают грибные «ведьмины» кольца.

Теперь представим ситуацию, когда Е может быть и больше и меньше Р. При Е = Р разгрузки потенциала не происходит, а меняется лишь качественное состояние территории, меняется ее «цвет». Если пороговый и потенциальный рельефы горизонтальны, то вся территория одновременно в момент достижения условия Е => Р перейдет в новое качественное состояние — изменит цвет. Если же пороговый или потенциальный рельеф расчленен (рис. 135), то к какому-то моменту на отрезках ab и cd поверхность будет находиться в одном качественном состоянии, а на отрезке bc — в другом. Появилась простейшая структура. Пример из этой серии — возникновение водоемов. Поверхность становится обводненной, когда уровень грунтовых вод (Е) превышает уровень земли (Р). Контур голубых водоемов и в природе и на карте соответствует линии, на которой выполняется условие Е = Р.

Зададим несколько пороговых уровней и соответственно несколько качественных состояние Р₁<Р₂<Р₃. Пусть состояние Р<Р₁ имеет желтый цвет, Р₁<Р<Р₂ — зеленый, Р₂<Р<Р₃ — салатный, Р₃<Р — белый. При горизонтальных рельефах (при равномерных условиях) вся область будет находиться в каком-то одном состоянии, пространственной структуры не будет. Если же задать наклонный потенциальный рельеф, например в виде конуса, в вершине которого Е>Р₃, то получим пространственную структуру, состоящую из вложенных цветных колец (рис. 136). А если этот конус рассечен пятью спускающимися с него глубокими лощинами, то мы получим рисунок из вписанных друг в друга цветных пятиконечных звезд. Простейший пример рисунков, выполненных в такой манере, — высотная поясность. Как только высота (E) достигает уровня Р₁ — желтые степи сменяются зеленым лесом, на уровне Р₂ проходит граница между лесом и альпийскими лугами, а на уровне Р₁ — граница белых вечных снегов.

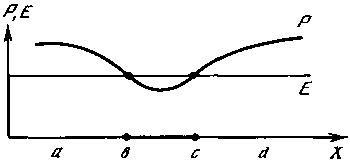
Рис. 135

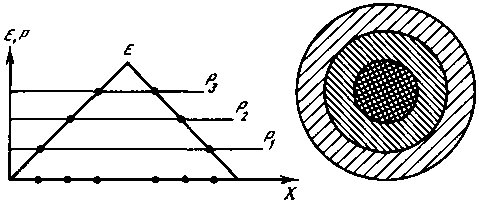
Рис. 136

Другой пример — цветные разводы на мыльном пузыре или на разползшемся по воде пятне от капли горючего. Е в данном случае — толщина пленки, а уровни Р задаются длиной световых волн, соответствующих цветам солнечного спектра. Если толщина пленки везде одинакова, то рисунок одноцветный. Если же она меняется, то появляется последовательное многоцветие. Как видим, наши Е и Р применимы не только для линий и точек.