Книга: Азбука рисунков природы

Параллельные и расходящиеся

Параллельные и расходящиеся

В этом и последующих разделах мы рассмотрим особенности формирования рисунков из линий на плоскости. Это могут быть различные сетчатые, ячеистые, древовидные рисунки, например сеть трещин, рисунки речной сети, транспортных магистралей и т. д.

Для этого класса структур различные механизмы формирования также можно свести к описанию закономерностей изменения абстрактных потенциальной и пороговой функций. Пороговая и потенциальная функции, рассматриваемые в предыдущих разделах, являлись скалярами, в любой точке пространства они могли быть охарактеризованы одним числом. Поэтому функции легко представлялись одномерными или двухмерными рельефами. В случае же с линейными элементами в каждой точке величина потенциальной функции в разных направлениях может быть различной — потоки напряжений нельзя охарактеризовать, не задав направлений.

Например, как появляются элементы гидрографической сети — эрозионные ложбины? Допустим, что но плоскому склону в направлении его уклона стекает распластанный водный поток. Как только в каком-то месте его скорость достигает величины, равной размывающей, на склоне образуется канавка, ложбина, она перехватывает поток и из-за этого еще больше углубляется — возникает линейный структурный элемент, который в своем окружении «разгружает» распластанный поток, стекающий по первоначальному уклону в этом направлении.

Другой пример — образование тропинок. Предположим, что в черте города расположен большой ровный пустырь, заросший невысокой травой. Этот пустырь постоянно в разных направлениях пересекают люди. Одно из направлений движений преобладающее. Пешеходы приминают траву, но, пока их поток относительно небольшой, трава успевает восстановиться и сплошность растительного покрова не нарушается. Но допустим, что со временем людской поток увеличивается до критической величины, и в какой-то части пустыря, где поток наиболее интенсивный, растительность начинает деградировать — появляется выбитая полоса. По выбитому месту идти легче, поэтому пешеходы, движущиеся в направлении, параллельном этой выбитой полосе, увидев ее, сворачивают и идут по ней. Происходит еще большая концентрация потока — образуется тропинка, которая на ширину видимости разгружает параллельный себе поток пешеходов.

Во многих случаях и для величины пороговой функции необходимо задавать направление. Например, прочность на разрыв у многих материалов в различных направлениях может сильно различаться (пример — деревянная доска трескается вдоль, а торец бревна — по радиусу или окружности). Соответственно трещины в таких материалах будут возникать не вкрест направлению максимальных растягивающих напряжений, а в том направлении, где в первую очередь напряжения достигнут величины прочности, наблюдаемой в этом же направлении.

У линейных элементов может быть специфична и разгрузка потенциальной функции. Вблизи элемента величина потенциала может разгружаться во всех направлениях, а может преимущественно или (лишь) в каком-то одном. Все это значительно усложняет анализ, формализацию и графическое выражение механизмов формирования рисунка. Тем не менее попытаемся это сделать. Оговорим, что составляющую потенциала для какого-то направления в точке пространства будем считать мерой возможности появления в данной точке структурного линейного элемента, ориентированного в этом направлении. В ряде случаев потенциал можно задать как вероятность появления в этом направлении элемента. Отметим, что направление, в котором наш потенциал максимален, может не соответствовать направлению реальных параметров. Так, например, трещины возникают в направлении, перпендикулярном направлению максимальных растягивающих напряжений.

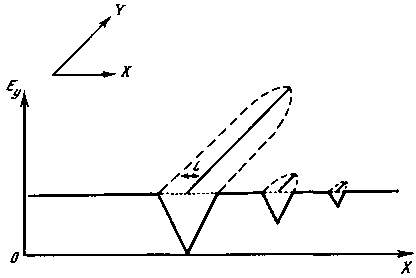
Рис. 55

Конкретные примеры мы пока рассматривать не будем, а сразу начнем с абстрактных схем. Будем задавать различные варианты пороговой и потенциальной функций, их динамики и условий разгрузки, получая в итоге различные рисунки.

Начнем наши примеры со структур, возникающих на плоскости xy в резко анизотропном потенциальном поле. Примем, что потенциал везде ориентирован в направлении y, во всех других же направлениях потенциал равен нулю. Пороговую функцию при этом зададим скалярной величиной; примем, что во всем рассматриваемом пространстве она одинакова. При этих условиях структурные элементы будут возникать там, где величина потенциала достигнет величины пороговой функции. Элементы при этом будут всегда прямыми линиями, ориентированными вдоль направления y. Примем, что на линии элемента разгрузка потенциала полная, ширина зоны разгрузки вокруг линейного элемента конечна и не превышает 2l, при этом величина разгрузки при удалении от элемента изменяется по линейному закону (рис. 55). Примем, что в вершине структурного элемента (у конца линии) ширина зоны разгрузки и ее «глубина» равны нулю и лишь на каком-то удалении от конца, допустим на расстоянии порядка 2l, она достигает конечной ширины и «глубины» — полностью разгружает потенциал (см. рис. 55).

В вершине структурного элемента возможно увеличение значений потенциала или снижение значений пороговой функции — «ослабление прочности», «концентрация напряжений». Из-за этого элемент (линия) может «по инерции» проникать в область, где E_y < P. Этот вариант рассмотрим позже, а пока примем, что вершина структурного элемента не может проникать в область пространства, где E_y < P.

Рассмотрим особенности формирования рисунка в пределах плоскости, ограниченной прямоугольником с вершинами А, В, С, D. Примем, что его стороны AD и ВС не оказывают влияния на потенциальную функцию, а стороны АВ и CD разгружают ее, как будто они являются структурными элементами. Пусть в пределах выделенного контура величина потенциальной функции будет везде одинакова.

Начнем наращивать потенциал. Его рельеф параллелен пороговому рельефу, поэтому условие E_y = P возникнет одновременно по всему контуру. Тогда первый структурный элемент (линия) может возникнуть в любом месте. Допустим, что структурные элементы развиваются моментально, тогда элемент быстро пересечет весь контур вдоль себя и в полосе шириной 2l разгрузит потенциал. Новый элемент образоваться здесь уже не сможет. За пределами же зоны разгрузки первого элемента в случайных местах будут возникать новые элементы. В итоге возникнет структура, состоящая из параллельных линий, расстояние между которыми изменяется от l до 2l (рис. 56, а). Если продолжать наращивание потенциала, то посередине между линиями первой генерации, в первую очередь в наиболее широких полосах, будут возникать линии второй генерации (рис. 56, б) и т. д. Во всех последующих рисунках в правом верхнем углу мы графически будем изображать условия задачи. Прямоугольник — это «карта» рельефа максимальных значений первоначально заданной потенциальной функции. Рельеф будет показан изолиниями и берг-штрихами, показывающими уклон. Если на карте нет изолиний, значит, рельеф горизонтальный. Рядом мы будем изображать индикатрису потенциала, показывающую относительные значения потенциала в координатах рисунка.

Теперь предположим, что элементы развиваются медленно. Тогда по всему полю в случайных местах, определяемых микрошероховатостью, будут возникать короткие растущие линии (штрихи). Пока они короткие (меньше 2l), их окружает узкая зона разгрузки, поэтому новые элементы могут возникать вблизи с предыдущим. Появление новых элементов и удлинение первоначальных приведет к тому, что вся поверхность перекроется зонами их разгрузки и развитие структуры остановится (рис. 57, а). Если после этого продолжать наращивать значения потенциала, то сразу же начнется удлинение элементов — они будут взаимопроникать в зону разгрузки других, встречных элементов. Возникнут условия конкуренции. Если встречаются два коротких элемента (меньше 2l) разной длины, то у более длинного зона разгрузки глубже, поэтому он будет проникать в зону разгрузки короткого элемента быстрее, чем короткий в его зону разгрузки. В итоге за счет преимущественного развития наиболее длинных элементов структура, изображенная на рис. 57, а, трансформируется в структуру, подобную приведенной на рис. 57, б. Если при соблюдении условия конечности максимальной ширины зоны разгрузки и дальше продолжать наращивание потенциала, то в итоге можно добиться того, что все элементы пересекут массив. После этого наращивание потенциала приведет к возникновению элементов второй генерации. Если же элементы могут постоянно углубляться и расширять зону разгрузки, то в условиях конкуренции мелкие элементы могут вырождаться.

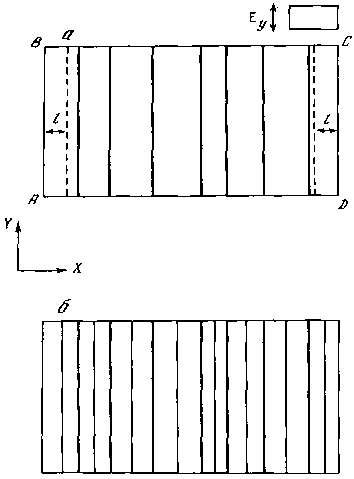
Рис. 56

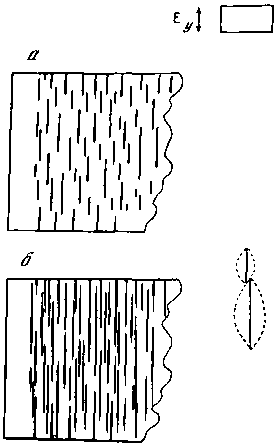
Рис. 57

Структуры, подобные изображенной на рис. 51, б, могут возникнуть и без дополнительного наращивания потенциала, если в вершине линий происходит его концентрация. За счет этого элементы могут проникать в зоны разгрузки других элементов.

Теперь для того же массива ABCD зададим другую геометрию поверхности потенциального рельефа. Он также будет плоским, но будет иметь общий наклон от линии АВ к CD. В этом случае равномерное наращивание значений потенциала приведет к тому, что в какой-то момент на границе зоны разгрузки стороны АВ выполнится условие E_y = P. Здесь возникнет элемент. После этого на расстоянии l от этого элемента (на краю его зоны разгрузки) в потенциальном рельефе возникнет новый горизонтальный гребень, на котором при дальнейшем наращивании значений потенциала появится новый элемент, и т. д. В итоге возникнет структура, состоящая из параллельных линий, удаленных друг от друга на расстояние l. В наиболее «старой» части структуры при этом возможно появление элементов более высоких генераций (рис. 58).

Если задать, что структурные элементы «углубляются» и расширяют свою зону разгрузки медленно, а потенциал нарастает относительно быстро, то новые структурные элементы могут появляться на расстоянии меньше, чем l, от предыдущего элемента. Причем чем выше скорость нарастания потенциала, тем меньше будет это расстояние. Плотная упаковка элементов первой генерации может исключить возникновение элементов более высоких генераций.

Другое условие: пусть в пределах массива потенциальный рельеф имеет общий наклон от линии AD к линии ВС. Линия AD — это гребень рельефа. Тогда при наращивании потенциала условие E_y = P выполнится на линии AD. Проникать в массив в направлении ВС линии не могут, там E_y < P. Поэтому на гребне перпендикулярно ему должны возникать коротенькие элементы, зона их разгрузки будет узенькой, и их здесь появится множество. Чем острее гребень, тем короче элементы и тем меньше ширина окружающих их зон разгрузки, тем соответственно большее их число расположится на гребне (рис. 59, а). Если наращивать значение потенциала, то граница области с условием E_y = P начнет смещаться в сторону ВС, граница «потянет» за собой вершины всех элементов (см. рис. 59, б). Острой конкуренции между ними при этом не возникнет, так как ни одна линия не может далеко «вырваться» за линию E_y = P и опередить другие элементы в разгрузке потенциала. При очень сильном наращивании потенциала в наиболее широких полосах между элементами этого рисунка могут появиться элементы второй генерации (рис. 59, б).

Представим теперь, что в пределах рассматриваемого массива потенциальный рельеф имеет общий наклон к точке С. Несложно показать, что структуры, образующиеся в этом случае при наращивании потенциала, принципиально не будут отличаться от уже рассмотренных структур, возникающих при наклоне порогового рельефа к линии CD (см. рис. 58), но упаковка линий будет более плотной. В случае, если такая структура не захватит все рассматриваемое пространство, будет виден косой фронт, соответствующий условию E_y = P (рис. 60).

Теперь при тех же условиях разгрузки рассмотрим закономерности формирования пространственных структур в пределах поля, ограниченного окружностью. Зададим, что потенциал во всех точках этого круга ориентирован вдоль его радиуса, т. е. элементы могут быть ориентированы только вдоль радиуса. В первом варианте допустим, что в пределах контура величина потенциала везде одинакова и равномерно возрастает. Тогда условие E_r = P возникнет по всему контуру. Примем, что структурные элементы развиваются моментально. Тогда первый элемент, возникнув в любом месте, рассечет круг пополам. Последующие же элементы, зарождаясь в случайных местах за пределами имеющихся зон разгрузки, будут развиваться лишь до тех пор, пока их вершина не дойдет до края какой-то зоны разгрузки. Образующаяся при этом структура показана на рис. 61, а. Если после этого продолжать наращивать значения потенциала, то эти элементы начнут достраиваться к центру круга, проникая своими вершинами в зоны разгрузки других элементов. В это же время на кромке длины окружности в центре наиболее широких промежутков будут зарождаться элементы второй генерации (рис. 61, б). Если задать, что в вершинах элементов происходит концентрация потенциала, то элементы проникнут к центру и без наращивания потенциала.

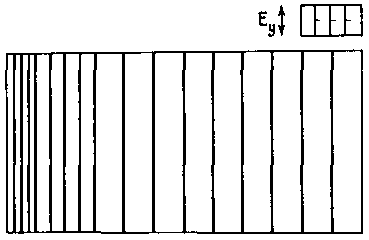
Рис. 58

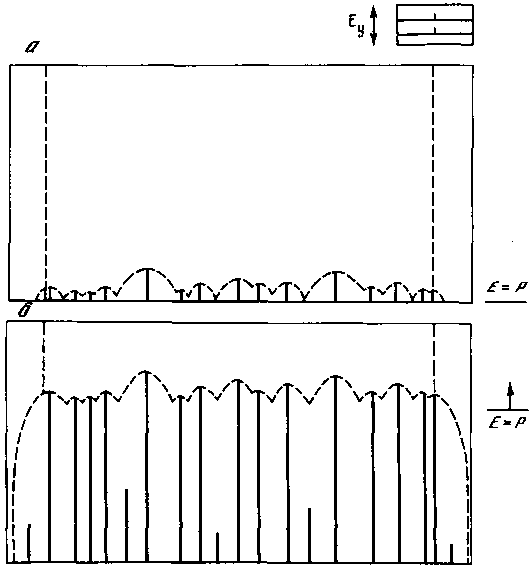
Рис. 59

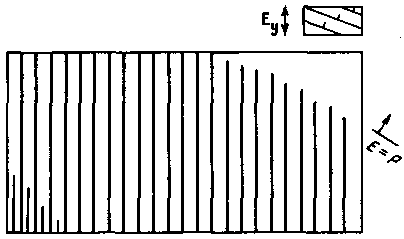
Рис. 60

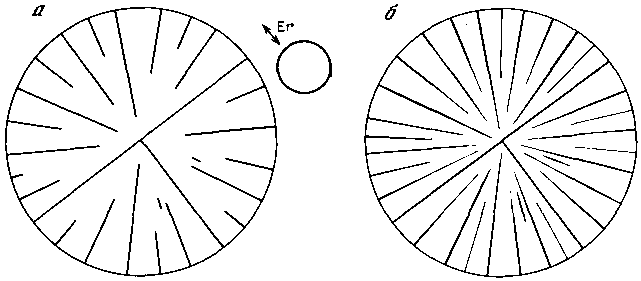
Рис. 61

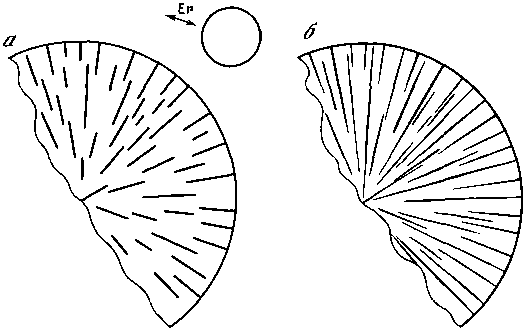
Рис. 62

Допустим, что структурные элементы развиваются медленно, тогда при достижении условия E_r = P возникнет множество коротких штрихов, которые своими зонами разгрузки перекроют все пространство (рис. 62, а). Если продолжать наращивать потенциал или задать, что в вершинах элементов происходит его концентрация, то элементы начнут удлиняться, проникая в режиме конкуренции своими вершинами в зоны разгрузки других элементов (см. рис. 62, б).

Зададим новую геометрию потенциального рельефа. Пусть это будет пологий конус с вершиной, расположенной в центре рассматриваемого круга. В этой точке в первую очередь выполнится условие E_r = P. В подобной точечной ситуации для описания реальных условий всегда необходимо учитывать микронеоднородность и то, что в той или иной степени концентрация потенциала у концов элементов будет происходить, и они из вершины могут проникать в область E_r < P. Из вершины может выйти три — пять лучей. Лишь в этом случае они будут развиваться за пределами зоны разгрузки других лучей (рис. 63). В точках, изображенных на врезках рис. 63, наращивание потенциала вызовет зарождение новых элементов. Дальнейшее наращивание потенциала в конечном итоге приведет к формированию структур, все элементы которых, кроме первых, являются элементами более высоких генераций. Закладывались они посередине между элементами предыдущей генерации. В итоге возникли высокоупорядоченные структуры. В случае несимметричного сочленения в вершине структура в пределах каждого из секторов будет высокоупорядоченной, но в целом несимметричной (см. рис. 63, а, б). Мы везде принимаем, что ширина зоны разгрузки конечна. Но можно задать, что по мере удлинения элемента ширина его зоны разгрузки постоянно увеличивается. В этом случае в последнем примере с потенциальным рельефом в виде конуса множество элементов не появится, даже линии первой генерации, секущие круг, могут разгрузить все пространство.

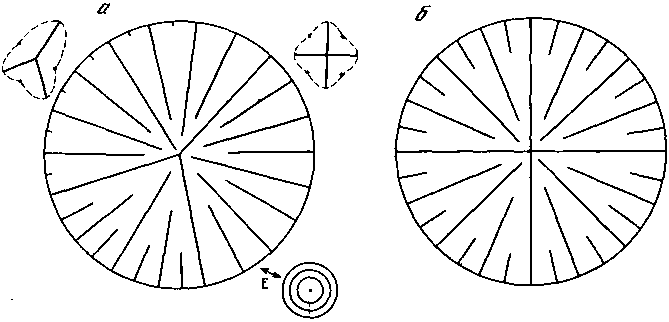
Рис. 63

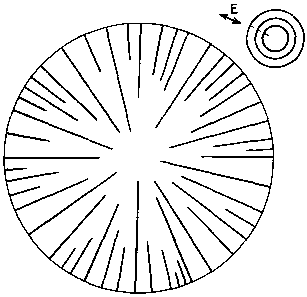
Рис. 64

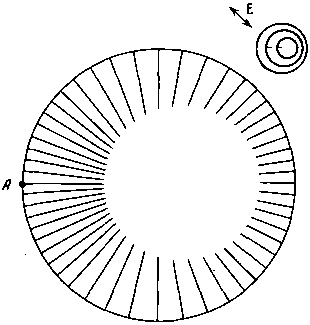
Рис. 65

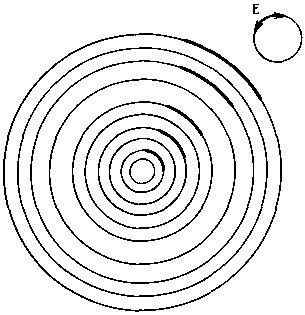
Рис. 66

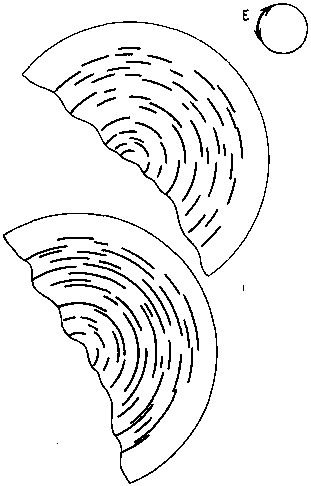
Рис. 67

Рис. 68

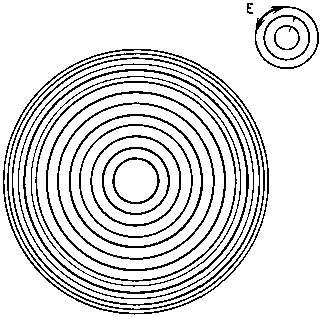
Рис. 69

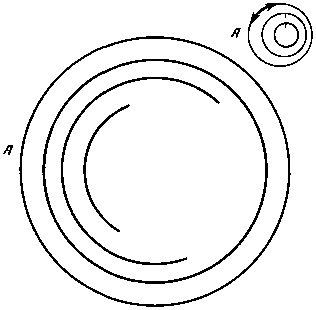
Рис. 70

Теперь представим, что потенциальный рельеф имеет форму перевернутого конуса. Условие E_r = P в этом случае первоначально выполнится по всей длине окружности. Здесь в случайных местах и будут зарождаться элементы. Их количество и расстояние между ними будут определяться степенью концентрации потенциала в их вершинах, скоростью их развития и темпами нарастания потенциала. Но во всех случаях высокой упорядоченности в структуре не будет. При наращивании потенциала эти элементы в режиме конкуренции за сокращающееся пространство будут удлиняться к центру (рис. 64).

Изменим условия. Пусть этот перевернутый конус будет немного наклонен. Тогда условие E_r = P первоначально выполнится лишь в одной точке А на периметре круга. Здесь образуется первый элемент. Со временем, по мере роста потенциала, у краев зоны разгрузки этого элемента на периметре круга возникнут два новых элемента. В свою очередь, и у края их зоны разгрузки появятся новые элементы и т. д. (рис. 65). Отметим, что при фиксированной скорости роста элементов и равномерном наращивании потенциала расстояние между элементами в рассматриваемом примере с конусом должно закономерно различаться. Минимальным оно будет возле первого и последнего элементов. После заложения всех элементов первой генерации дальнейшее наращивание потенциала приведет к их удлинению к центру круга и к заложению элементов новой генерации.

А теперь изменим потенциальную функцию. Зададим, что во всех точках в пределах круга значима лишь составляющая, ориентированная перпендикулярно радиусу, т. е. элементы могут быть представлены только окружностями или их отрезками. Структуры, которые при этом будут возникать, изображены на рис. 66—70. Определяющие их условия соответствуют условиям, принятым для структур, изображенных на рис. 61—65 соответственно.