Книга: Как работает Вселенная: Введение в современную космологию

2.7.2. Исследование решений

2.7.2. Исследование решений

Рассмотрим смысл и свойства решений Фридмана. Прежде всего перейдем от констант А и В к величинам с более четким физическим смыслом. Выберем опорный момент времени в системе наблюдателя, неподвижного по отношению к окружающей среде. Назовем этот момент текущей эпохой или «сейчас». Снабдим все значения, относящиеся к этому моменту, индексом 0. Мы уже делали это раньше, когда ввели параметр Хаббла H0 – текущее значение зависящей от времени постоянной Хаббла H. Следующей используемой величиной будет так называемый параметр плотности материи ?m = ?/?крит. Как числитель, так и знаменатель этого отношения зависят от времени согласно формулам (2.8) и (2.11). Следовательно, параметр плотности вещества тоже зависит от времени. Обозначим его текущее значение ?m0. Нам также понадобится текущее значение радиуса сферы r0, играющее роль текущего значения масштабного фактора.

Применив формулы (2.4) и (2.7) к текущей эпохе, мы получаем:

B = ?0r03 = ?m0 ?c 0 r03 = 3H02?m0 r03/8?G. (2.14)

Из (2.10) и (2.11) определим

Из уравнения (2.15) мы еще раз убеждаемся, что случай ?m > 1 соответствует А < 0, т. е. закрытой модели, в которой Вселенная в конечном итоге опять собирается в точку, случай ?m < 1 соответствует открытой модели с А > 0, а ?m= 1 соответствует плоской модели с А = 0.

Подставляя уравнения (2.14) и (2.15) в уравнение (2.12), мы получаем:

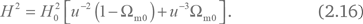
Здесь мы ввели относительный масштабный фактор u = r/r0, который может быть легко преобразован при r < r0 в красное смещение z простым соотношением 1/u = 1 + z.

Уравнение (2.16) полностью описывает зависимость H(u) или H(z). В современную эпоху u = 1, и оно выполняется автоматически. Проанализируем зависимость постоянной Хаббла от относительного масштабного фактора или красного смещения z.

При ?m = 1 (плоская модель) имеем H = H0u–3/2, что соответствует монотонному уменьшению Н, стремящемуся к нулю при u ? ?. При ?m < 1 (открытая модель) постоянная Хаббла также снижается, но медленнее. При ?m > 1 (закрытая модель) первый член в скобках отрицателен, а второй – положителен. Второй член уменьшается быстрее, чем первый. Таким образом, если бы эта модель допускала большие значения u, то правая часть уравнения (2.16) в конечном итоге стала бы отрицательной, что невозможно. Таким образом, относительный масштабный фактор Вселенной увеличивается до тех пор, пока постоянная Хаббла не становится равной нулю, а после этого уменьшается. Мы можем найти максимальный масштабный фактор, приравняв выражение в квадратных скобках к нулю:

umax = rmax/r0 = ?m0/(?m0 – 1). (2.17)

Чтобы найти зависимости от времени, нам нужно подставить уравнения (2.14) и (2.15) в уравнение (2.13), которое сводится к

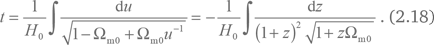
Все, что требуется, чтобы вычислить этот интеграл, – заглянуть в хороший справочник. В простейшем случае плоской модели (?m0= 1) мы получаем:

Значение константы интегрирования выбрано таким образом, чтобы момент t = 0 соответствовал Большому взрыву.

Для открытой модели (?m0 < 1) мы имеем:

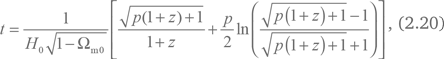
где p = ?m0/(1 – ?m0) > 0.

Для закрытой модели (?m0 > 1) мы имеем другое громоздкое выражение

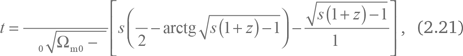
где s = ?m0/(?m0 – 1) > 1.

Мы использовали эти формулы для построения рис. 2.2. Теперь построим его еще раз, как рис 2.8, добавив масштабы на осях. Мы используем значение H0 = 68 (км/с)/Мпк, которое, впрочем, влияет только на временной масштаб графика. Мы использовали довольно экстремальные значения ?m0= 0,5 и ?m0= 1,5 для открытой и закрытой моделей.

Уравнение (2.21) дает нам промежуток времени от Большого взрыва до момента, когда замкнутая Вселенная достигает своего максимального размера, и равный ему промежуток времени с этого момента до Большого хруста:

Общее время жизни замкнутой Вселенной равно 2?T.