Книга: Как работает Вселенная: Введение в современную космологию

2.7.4. Материя с ненулевым давлением в расширяющейся Вселенной

2.7.4. Материя с ненулевым давлением в расширяющейся Вселенной

Рассмотрим объем V, заполненный материей с плотностью энергии ? и давлением р. Оба параметра изменятся, если мы сожмем или расширим этот объем, и сделают они это согласованно. Зависимость между давлением и плотностью энергии называется уравнением состояния. Мы уже обсуждали это в разделе 1.3. Уравнение состояния называется баротропным, если давление является функцией только плотности энергии p = p(?).

Начнем с получения зависимости этих величин от объема. Для случая пылевидной материи эта зависимость имеет вид (2.8). Для того чтобы получить ее для материи с баротропным уравнением состояния, мы используем закон сохранения энергии, он же первый закон термодинамики, который имеет вид

dE = dQ ? dA. (2.29)

Здесь E = ?V – внутренняя энергия материи, dE – ее изменение, dQ – количество тепла, поглощенного этой материей, а dA = pdV – механическая работа, совершенная материей в ходе ее расширения.

Термодинамический процесс с dQ = 0 называется адиабатическим. Он не сопровождается передачей тепла внутрь или наружу системы. Чтобы сделать процесс адиабатическим, в лабораториях используется специальное оборудование для предотвращения передачи тепла в ту или иную сторону. В повседневной жизни мы используем термос, чтобы горячие или холодные напитки хранились в практически адиабатических условиях. Но никто не нуждается в термосе, чтобы сделать адиабатическим космологическое расширение. Действительно, температура в однородной Вселенной везде одинакова, поэтому не происходит никакой передачи тепла из одного места в другое, а передача тепла наружу невозможна, ведь Вселенная не имеет никакого «снаружи».

С учетом этого уравнение (2.29) сводится к

dE = d(?V) = ?dV +Vd? = ?dA = ? pdV, (2.30)

или

Vd? = –(? + p)dV. (2.31)

Зная баротропное уравнение состояния p = p(?), мы можем легко найти его решение:

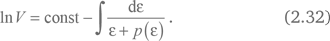
Особенно просто рассмотреть случай весьма популярного среди космологов уравнения состояния

p = w?, w = const. (2.33)

Из формул (2.32), (2.33) и учитывая, что V ~ r3, получаем:

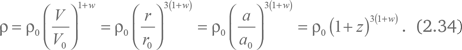
Здесь ?0 – плотность материи в тот момент, когда сфера имела размер r0 или Вселенная имела масштабный фактор a0. В релятивистской космологии это просто настоящий момент, или «сейчас». Так, плотность материи ? зависит от ее текущего значения ?0 и отношения размеров, выраженного через красное смещение z. Случай пылевидной материи без давления соответствует w = 0. Подставляя это значение в уравнение (2.34), мы, как и следовало ожидать, получим уравнение (2.8).

Особый случай w = –1 или p = –? дает интересный результат. Уравнение (2.31) гарантирует, что в этом случае плотность энергии постоянна. Расширение или сжатие Вселенной не меняет ни плотность энергии ?, ни плотность вещества ?, ни его давление p. Этот случай описывает космологическую постоянную ?.