Книга: Как работает Вселенная: Введение в современную космологию

2.5. Геометрия Вселенной

2.5. Геометрия Вселенной

Решения Фридмана для уравнений Эйнштейна без космологической постоянной описывают три возможных типа Вселенной. В дополнение к различиям, которые мы рассмотрели в предыдущем разделе, они также имеют различные знаки пространственной кривизны. Это наиболее фундаментальное свойство моделей Фридмана.

Что такое пространственная кривизна? Давайте еще раз применим двумерную аналогию. Лист бумаги имеет нулевую пространственную кривизну, так как он является плоским, т. е. представляет собой часть плоскости. Плоская поверхность подчиняется правилам евклидовой геометрии (тому виду геометрии, которому учат в школе). Как следует из названия, плоская Вселенная действительно плоская и ее пространственная кривизна тоже равна нулю. Сферические поверхности, такие как поверхность земного шара, имеют положительную пространственную кривизну. Это двумерный аналог замкнутой модели.

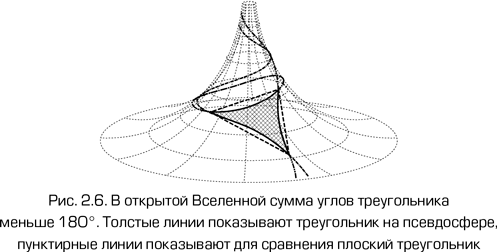
Есть более сложные седлообразные поверхности, которые имеют отрицательную пространственную кривизну, наиболее известной из которых является так называемая псевдосфера. Они представляют собой двумерные аналоги открытой модели. В двух последних случаях, когда кривизна ненулевая, евклидова геометрия уже не работает. Другими словами, зная пространственную кривизну, мы можем определить, какое из решений Фридмана описывает реальный мир.

Как можно узнать пространственную кривизну Вселенной? Если бы Вселенная не расширялась или мы могли бы перемещаться с бесконечной скоростью, это можно было бы сделать достаточно просто. Приведем аналогию. Представим двумерных существ, живущих на поверхности сферы. Их мир не имеет границ, но имеет вполне конечную площадь – 4?R2. Любую точку можно считать центром мира. Отношение длины окружности к радиусу меньше 2?. Более того, если мы выберем произвольную точку, скажем полюс, и начнем проводить вокруг нее окружности все большего радиуса (параллели), то вначале их длина будет расти, достигнет максимума на экваторе, а потом будет падать (см. рис. 2.4). Длина внешней окружности будет меньше длины вложенной в нее внутренней. Если заменить окружности заборами, то существо, которое их начнет красить снаружи, через некоторое число покрашенных заборов обнаружит, что окружено последним забором со всех сторон, причем окружено с наружной стороны забора.

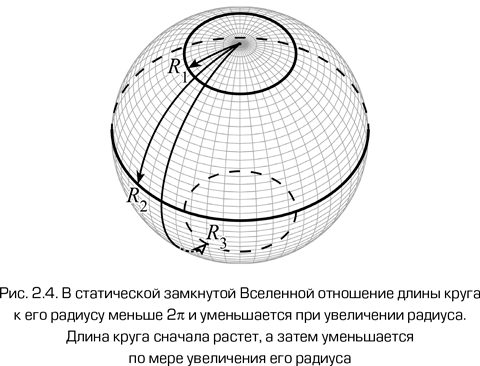
В трехмерном пространстве с положительной кривизной отношение площади сферы к квадрату радиуса будет меньше 4?. Площадь концентрических сфер с увеличением их радиуса вначале растет, потом падает.

Если кривизна равна нулю, то двумерные существа живут на плоскости, а трехмерные (мы) – в плоском пространстве. Работает (в идеальном случае) евклидова геометрия, отношение площади сферы к квадрату радиуса равно 4?, нет границ, объем Вселенной бесконечен.

Если кривизна отрицательна, то отношение площади сферы к квадрату радиуса будет больше 4?. Площадь концентрических сфер с увеличением их радиуса всегда растет. Нет границ, объем бесконечен.

Данные наблюдений не позволяют с уверенностью исключить ни один из этих вариантов. Но они показывают, что Вселенная либо плоская, либо достаточно близка к плоской. Этот вариант выделен и из теоретических соображений, как будет объяснено в разделе 5.

Для определения кривизны мы могли бы также рассматривать достаточно большие треугольники и измерять сумму их углов. Если она равна 180°, мы имеем дело с плоским пространством. Если она больше, кривизна положительна, как показано на рис. 2.5. Если меньше, кривизна отрицательна. Интересно, что подобный метод предложил еще Карл Фридрих Гаусс, который думал над практической реализацией этого метода, причем в качестве вершин треугольника предлагал использовать три горные вершины.

Но перейдем к реальному миру. Пространство на масштабах, в которых существует человечество, не является ни однородным, ни изотропным. Например, если мы построим треугольник на плоскости, перпендикулярной к Солнцу, точнейшие измерения показали бы, что сумма углов треугольника больше 180°. Естественно, в качестве сторон треугольника выступают лучи света в вакууме. Если же повернуть эту плоскость так, чтобы она проходила через Солнце, то сумма углов треугольника стала бы меньше 180°. Это следует из анализа метрики Шварцшильда, описывающей поле сферически симметричного тела в ОТО.

Поэтому проводить описанные здесь эксперименты имеет смысл только на масштабах, превышающих масштабы неоднородностей во Вселенной. Иными словами, на масштабах, существенно превышающих размеры нашей Галактики. Однако в идеальном случае однородной изотропной Вселенной мы можем рассматривать подобные мысленные эксперименты, чтобы лучше понять различие между разными типами расстояний, вводимых в кривом пространстве. Для реальных же наблюдений совершенно необходимы большие масштабы. И все описанные ниже наблюдения – по вспышкам сверхновых, по неоднородностям реликтового излучения, по барионным акустическим колебаниям – удовлетворяют этому требованию.

Отметим один забавный нюанс, касающийся замкнутой модели Вселенной. Если бы Вселенная не расширялась, а скорость света была бесконечной, то, посмотрев в сверхмощный телескоп, мы могли бы увидеть собственный затылок. Это явление аналогично тому, что путешественник, идущий строго на запад, в конце концов вернется в исходную точку. С этим обстоятельством были связаны весьма наивные наблюдения, предпринятые некоторыми астрономами достаточно давно. Они наводили свой телескоп в сторону, прямо противоположную наиболее далеким из известных в то время астрономических объектов, в попытке увидеть их с другой стороны. На самом деле знакомство с релятивистской космологией не в популярном изложении избавило бы их от напрасных наблюдений. Дело в том, что даже если реальная Вселенная замкнута, она расширяется, а потом сжимается. Время, необходимое свету на то, чтобы обогнуть всю замкнутую Вселенную, как показывают расчеты, больше времени существования такой Вселенной от Большого взрыва до Большого хруста.