Книга: Как работает Вселенная: Введение в современную космологию

2.4. Модели Фридмана

Закон Хаббла имел столь важное значение для космологии, поскольку эта зависимость следовала из теоретических предсказаний, сделанных незадолго до его открытия.

В 1922 г. в Петрограде (ныне Санкт-Петербург) русский физик Александр Фридман получил решение уравнения Эйнштейна, описывающее всю Вселенную, но не содержащее космологической постоянной. Особенность этого решения состояла в том, что Вселенная была динамической, т. е. вначале расширялась, а затем в зависимости от своей первоначальной плотности либо продолжала вечно расширяться, либо расширение сменялось сжатием. В 1927 г. это же решение было получено бельгийцем Жоржем Леметром, а в 1935 г. – американцем Говардом Робертсоном и британцем Артуром Уокером. В англоязычной литературе это решение часто называют решение FLRW по их инициалам (в старых книгах иногда встречается аббревиатура FRW, из которой несправедливо исключен Леметр). Мы в этой книге называем его решением Фридмана, признавая приоритет ученого.

Это решение является чрезвычайно важным, поскольку лежит в основе всех современных космологических теорий, которые комбинируют его идею с идеей космологической постоянной. Хотя сегодня известно, что исходное решение Фридмана не описывает реальную Вселенную, оно очень важно для понимания современных космологических моделей. Поэтому стоит знать его основные свойства. По этой причине мы даем его подробное описание в разделах повышенной сложности.

Фридман и его последователи применили уравнения ОТО Эйнштейна для описания однородной и изотропной Вселенной. Напомним, что в таком мире нет избранного места или предпочтительного направления, каждая точка не лучше и не хуже любой другой, как и каждое направление. Этих требований достаточно для того, чтобы получить, например, закон Хаббла как наиболее общее решение для скорости разбегания галактик, что мы и сделали в разделе 2.3.

Решение Фридмана описывает три физически различные ситуации, отличающиеся величиной отношения плотности материи Вселенной к так называемой критической плотности, зависящей от постоянной Хаббла. Точная формула для критической плотности (2.11) будет дана чуть позже в «продвинутом» разделе. Это отношение называется параметром плотности вещества и обозначается ?m. Если этот параметр меньше единицы, Вселенная имеет бесконечный объем и расширяется вечно, причем скорость разбегания любой галактики стремится к положительному значению. Такая ситуация называется открытой моделью, или открытой Вселенной Фридмана.

Когда параметр плотности равен единице, Вселенная так же бесконечна и вечно расширяется, но скорость разбегания любой галактики стремится к нулю. Такая ситуация называется плоской моделью, или плоской Вселенной Фридмана, и отличается от открытой модели ее асимптотическим поведением в будущем. Открытая Вселенная расширяется быстрее, чем плоская Вселенная.

Совершенно иная ситуация возникает тогда, когда параметр плотности больше единицы. В этом случае, который называется закрытой, или замкнутой моделью Фридмана, Вселенная имеет конечный объем, но не имеет границ или краев. Чтобы понять, как такое возможно, представьте себе земной шар или любую другую сферу. Площадь земной поверхности конечна, но нигде нет «края света». Закрытая Вселенная выглядит точно так же, но в трех измерениях[30]. В какой-то момент она перестает расширяться и начинает сжиматься, что сопровождается изменением знака постоянной Хаббла, а через некоторое время снова сжимается в точку, точнее в сингулярность, называемую Большой хрусть[31].

Все три модели начинаются с начальной сингулярности, называемой Большим взрывом, которую можно рассматривать как возникновение Вселенной.

Следует отметить, что, хотя и плотность вещества и критическая плотность изменятся с течением времени, отношение ?m не может пересечь граничное значение, равное единице. Другими словами, тип модели – открытая, плоская или закрытая – фиксирован и не может измениться.

Проиллюстрируем свойства этих моделей рис. 2.2, на котором показано, как их основные параметры (масштабный фактор и постоянная Хаббла) изменяются со временем. Сразу после Большого взрыва постоянная Хаббла была бесконечно большой, а масштабный фактор бесконечно малым. В закрытой модели непосредственно перед Большим хрустом постоянная Хаббла стремится к значению, равному минус бесконечности, а масштабный фактор вновь становится бесконечно малым. Естественно, постоянная Хаббла обращается в ноль, когда замкнутая Вселенная достигает своего максимального размера.

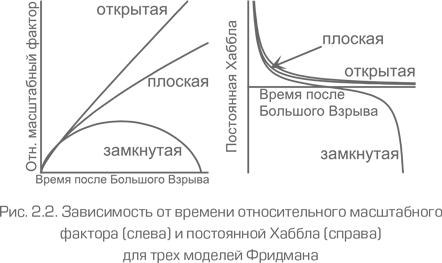
Из того факта, что Вселенная сейчас расширяется, мы приходим к выводу, что она описывается либо открытой, либо плоской моделями, либо закрытой моделью в фазе расширения. В любом случае ее масштабный фактор до сих пор рос монотонно. График его изменения от Большого взрыва до текущей эпохи показан на рис. 2.2. Длина волны фотона, излученного давно, когда Вселенная была меньше, увеличилась с тех пор в 1/u раз, где u – относительный масштабный фактор в ту эпоху, когда был излучен свет. Поэтому красное смещение фотона, т. е. его z-фактор, равно z = 1/u – 1. Чем старше свет, излученный объектом, тем дальше объект и тем больше его красное смещение. Именно поэтому красное смещение является хорошим индикатором расстояния.

Вопрос: Как смещался бы спектр, если бы мы жили в сжимающейся замкнутой Вселенной?

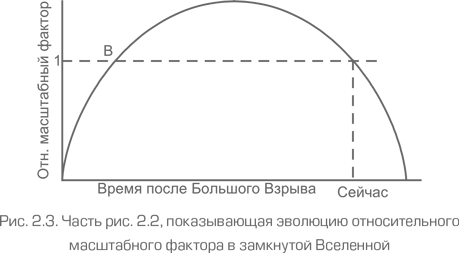
Ответ: Начнем с построения графика зависимости относительного масштабного фактора от времени для этого случая, охватив период от Большого взрыва до современной эпохи. Это, естественно, часть графика, приведенного на рис. 2.3. Мы видим, что масштабный фактор сначала растет от нуля в момент Большого взрыва до некоторого значения amax, большего единицы, а затем уменьшается до единицы в современную эпоху. Естественно, что в некоторой точке B во время фазы расширения масштабный коэффициент тоже равен единице. Длина волны света, испускаемого в точке В, вначале увеличивается в amax раз, а затем уменьшается в amax раз, и свет приходит к нам сейчас с точно такой же длиной волны, с какой он был испущен. Таким образом, любой свет, испущенный до момента времени B, наблюдался бы нами с точно такой же длиной волны, какую он имел в точке В. Это означает, что спектр любого объекта, излучившего свет между Большим взрывом и точкой В, будет иметь красное смещение. Таким образом, для любого света, испущенного до момента B, мы можем использовать те же формулы, что и в случае расширяющейся Вселенной.

Длина волны любого света, излучаемого после точки B, будет увеличиваться меньше, чем она станет уменьшаться впоследствии на этапе сжатия. Это означает, что его наблюдаемая длина волны будет короче, чем излучаемая, т. е. его спектр будет смещен в фиолетовую область. Достаточно очевидно, что максимальное синее смещение будет наблюдаться для света, излучаемого в тот момент времени, когда Вселенная имела максимальный масштабный фактор. Если формально применять формулу для красного смещения в расширяющейся Вселенной, мы получим отрицательную величину z. Более того, любое такое значение z будет соответствовать двум различным моментам времени и, следовательно, двум различным расстояниям. Это вызвано тем фактом, что Вселенная обретает соответствующий масштабный фактор дважды: во время расширения от точки В до максимального размера и при сжатии от максимального размера до современной эпохи.

Астрономы, живущие в этом мире, наблюдали бы объекты, у которых синее смещение увеличивается с расстоянием, затем при дальнейшем увеличении расстояния до объектов синее смещение уменьшается до нуля и сменяется красным смещением. Эти астрономы, несомненно, имели бы массу проблем при определении расстояний до удаленных объектов. К счастью, в соответствии с современными ограничениями на значения космологических параметров наша Вселенная никогда не будет сжиматься.