Книга: Как работает Вселенная: Введение в современную космологию

2.7.1. Космологическая эволюция без космологической постоянной

2.7.1. Космологическая эволюция без космологической постоянной

Рассмотрим вначале простейшую модель, когда Вселенная равномерно заполнена пылевидной материей, т. е. материей, не имеющей давления, с плотностью ?(t). Выберем произвольную точку, которую будем считать центром Вселенной. Естественно, мы можем взять любую другую точку и назначить ее в качестве центра Вселенной, но из-за однородности Вселенной уравнения и их решения будут теми же.

Рассмотрим сферу радиуса r(t) вокруг этого центра, привязанную к материи и расширяющуюся вместе с ней по закону Хаббла (2.1). Ни один атом или частица материи не могут пересечь эту сферу. Все, что было внутри сферы, остается внутри навсегда, все, что снаружи сферы, всегда будет снаружи, а то, что на поверхности, остается на поверхности. Радиус сферы мал по сравнению со значением c/H, поэтому его изменение нерелятивистское, и мы можем использовать простейший вариант закона Хаббла (2.1) v(t) = H(t)r(t), где v(t) = dr(t) / dt – это скорость расширения сферы с радиусом r(t). Таким образом, H(t) = dr(t) / dt r^?1(t).

Объем шара равен 4?r3/3, масса пылевидного вещества внутри этой сферы равна M = 4??r3/3. Эта масса остается постоянной во время расширения, поэтому, вводя константу B = 3M/4?, мы получаем закон изменения плотности со временем в виде

?(t) = Br(t)–3. (2.8)

Как вы можете видеть, до сих пор не возникло никаких «математических кошмаров». Следующим шагом является получение уравнения, описывающего расширение Вселенной, и выведение из него зависимостей r(t) и H(t).

Прежде чем мы к этому приступим, рассмотрим куда более простую родственную задачу. Где-то в космосе есть сферически симметричная планета с массой М и радиусом R, которая не имеет никакой атмосферы и не вращается, поэтому влиянием этих факторов можно пренебречь. Ее обитатель пинает ногой, щупальцем или псевдоподием футбольный мяч массой m вертикально вверх со скоростью V. Как будет двигаться мяч? Очевидно, что он будет двигаться в радиальном направлении от центра планеты. Улетит ли он в космос или упадет обратно на поверхность планеты (рис. 2.7)?

Как мы можем узнать, что произойдет? Достаточно использовать закон сохранения энергии. Суммарная энергия мяча равна сумме кинетической и потенциальной энергий. Кинетическая энергия в любой момент равна mv2/2, где v – это текущая скорость мяча. Потенциальная энергия гравитационного взаимодействия мяча и планеты равна – GMm/a, где G – гравитационная постоянная, a – текущее расстояние между мячом и центром планеты. Потенциальная энергия отрицательна вблизи планеты и становится равной нулю, если мяч удаляется от планеты на очень большое расстояние. Кинетическая энергия шара всегда неотрицательна. Таким образом, для того чтобы мяч улетел в космос, его полная энергия тоже должна быть неотрицательной. Так как полная энергия сохраняется, это также относится и к его начальной энергии Е, равной

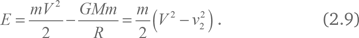
Значение

Как ни странно, эти случаи соответствуют также и трем основным сценариям космологического расширения. Вернемся к сфере из пылевидной материи и рассмотрим частицу массы m, которая все время находится на поверхности. В какой-то момент времени ее кинетическая энергия равна mv2/2 = mH2r2/2. Гравитационная потенциальная энергия обеспечивается только взаимодействием с веществом внутри сферы и равна – GMm/r = –4?G?mr2/3. Полная энергия равна

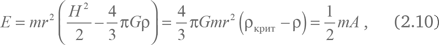
где A = const из закона сохранения энергии. Мы ввели обозначение для критической плотности материи

?крит = 3H2/8?G. (2.11)

Обратите внимание, что величина ?крит зависит от величины постоянной Хаббла H и изменяется во времени. В настоящее время она равна 1,88?10–26 h2 кг/м3, где h = H0/(100 (км/с)/Мпк). Используя величину h, полученную из астрономических наблюдений, можно получить ?крит = (8,62 ± 0,12)?10?27 кг/м3. Чему это соответствует? Самая разреженная среда, с которой когда-либо сталкивалось человечество, – это межпланетное пространство в Солнечной системе. Его плотность в районе орбиты Земли мала и составляет примерно 10–20 кг/м3 (6 протонов на 1 см3), что более чем в 80 млн раз больше критической плотности.

Разность между плотностью вещества ? и критической плотностью всегда имеет тот же знак, противоположный знаку константы А. При А > 0 всегда выполняется условие ? < ?крит. Энергия частицы (2.10) положительна, и, следовательно, частица может достичь бесконечности. Ее скорость уменьшается, стремясь к положительному предельному значению v = ?A. Вселенная вечно расширяется, начиная с Большого взрыва, и без Большого хруста/хрустя. Этот случай соответствует открытой модели Фридмана. При А = 0 имеем ? = ?крит и в любой момент вечного расширения частица имеет нулевую энергию и может достигать бесконечности, но с нулевой предельной скоростью. Это плоская модель Фридмана. Если А < 0, то всегда ? > ?крит и энергия частицы отрицательна. Она не может достичь бесконечности. Рано или поздно расширение Вселенной останавливается и сменяется сжатием. Это замкнутая модель Фридмана.

Как видим, все три версии космологической модели Фридмана – открытая, закрытая и плоская – можно объяснить столь же легко, как движение камня, брошенного вверх. Чтобы улететь бесконечно далеко, скорость камня должна быть равна второй космической скорости (это соответствует плоской модели) или превышать ее (открытая модель). Камень, брошенный медленнее, сначала летит вверх, а затем начинает падать вниз (закрытая модель). Тем не менее в рамках нерелятивистской космологии мы не можем определить, что замкнутая, плоская и открытая модели имеют соответственно положительную, нулевую и отрицательную пространственную кривизну. Это возможно только с помощью релятивистской космологии, основанной на ОТО.

Подставляя уравнение (2.8) в уравнение (2.10), мы получаем уравнение Фридмана для Вселенной, заполненной пылевидной материей, без космологической постоянной и зависимости H(r):

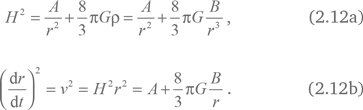
Решив их, мы получаем зависимости r(t) и H(t):

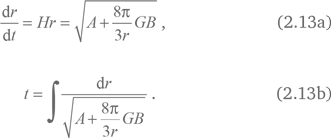
Вместе с зависимостью ?(t), определяемой формулой (2.8), они завершают описание трех возможных сценариев космологической эволюции в рамках нерелятивистской космологии.