Книга: Наша математическая вселенная

Исследование мультиверса IV уровня

Исследование мультиверса IV уровня

Наши ближайшие соседи

Потратим немного времени на знакомство с мультиверсом IV уровня и «зоопарком» содержащихся в нём математических структур. Начнём с ближних окрестностей. Хотя мы ещё не знаем точно, в какой математической структуре живём, нетрудно представить себе множество небольших её модификаций, дающих другие корректные математические структуры. Стандартная модель физики элементарных частиц включает определённые симметрии, которые математики обозначают так: SU(3) ? SU(2) ? U(1), и если заменить их иными симметриями, получится другая математическая структура с частицами иных типов и силами, где кварки, электроны и фотоны заменены иными сущностями с новыми свойствами. В некоторых математических структурах нет света, а в других отсутствует гравитация. В эйнштейновском математическом описании пространства-времени числа 1 и 3, соответственно задающие количество временных и пространственных измерений, могут быть заменены иными значениями по выбору.

В гл. 6 мы обсудили, как в рамках одной математической структуры с единственным набором фундаментальных законов физики инфляция может порождать различные эффективные физические законы в разных частях пространства, образуя тем самым мультиверс II уровня. Сейчас мы говорим о чём-то более радикальном, где даже фундаментальные законы могут отличаться и где нет, например, квантовой механики. Если теорию струн можно строго определить математически, то существует математическая структура, для которой теория струн является верной «теорией всего», но для всего остального в мультиверсе IV уровня это не так.

Чтобы оценить мультиверс IV уровня, надо раскрепостить воображение, освободиться от предубеждений относительно того, какими должны быть законы физики. Рассмотрим пространство и время. Вместо того чтобы быть непрерывными, как предполагается для нашего мира, они могут оказаться дискретными, как в «Пэкмене» и «Тетрисе» или в игре «Жизнь» Джона Конвея, где движения характеризуется лишь резкими скачками. Если отключить подачу команд пользователя так, чтобы эволюцию во времени можно было рассчитывать детерминистически, все эти игры отвечают корректным математическим структурам. На рис. 12.3 показан упоминавшийся в гл. 3 трёхмерный клон «Тетриса» под названием FRAC, написанный мной с приятелем Пером Бергландом в 1990 году. Если запустить его и не трогать клавиатуру (много очков с такой стратегией не набрать), то игра от начала до конца определяется простыми математическими правилами, заложенными в программу. Они делают её математической структурой, входящей в мультиверс IV уровня. Часто встречаются рассуждения о том, что даже в нашей Вселенной пространство-время может проявлять своего рода дискретность, скрывающуюся в столь малых масштабах, что мы до них ещё не добрались.

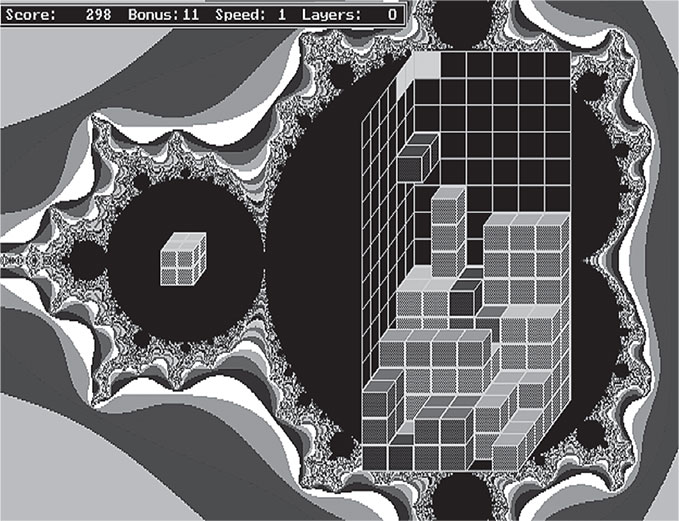
Рис. 12.3. FRAC, трёхмерный клон «Тетриса», реализует математическую структуру, где пространство и время дискретны, а не непрерывны.

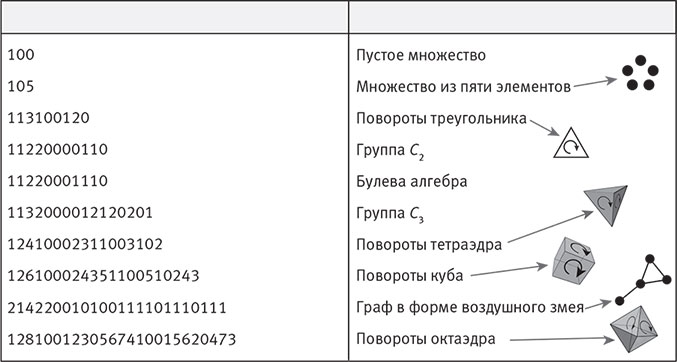
Рис. 12.4. Компьютерная программа может автоматически генерировать упорядоченный список конечных математических структур, где каждая кодируется последовательностью цифр. В таблице показаны некоторые примеры, заданные при помощи схемы кодирования из моей статьи 2007 года. Слова и диаграммы во второй колонке — это избыточный «багаж», отражающий способы, какими люди называют и иллюстрируют эти структуры.

Или даже так: существует множество математических структур, где нет ни пространства, ни времени, а значит, не имеет и смысла говорить, будто в них что-то происходит. Большинство структур, примеры которых приведены на рис. 12.4, как раз такого типа. Скажем, внутри абстрактного додекаэдра ничего не происходит, поскольку эта математическая структура не содержит времени.

Наш «почтовый индекс» в мультиверсе IV уровня

Как отмечалось в гл. 10, математическая структура — это множество абстрактных элементов с отношениями между ними. Для более систематического изучения мультиверса IV уровня нам понадобится написать компьютерную программу, которая автоматически генерирует список существующих математических структур, начиная с простейших. На рис. 12.4 показаны десять строк этого списка, составленного с помощью схемы кодирования, которую я описал в статье 2007 года о математической Вселенной.[84] Детали этого метода здесь несущественны, кроме того замечательного свойства, что любая математическая структура с конечным числом элементов обязательно появится в этом списке. А значит, любую из этих математических структур можно задать одним числом — её номером в списке.

Для конечных математических структур все отношения можно описать конечными таблицами чисел, распространяющими идею таблицы умножения на другие типы отношений. Для структур с очень большим числом элементов эти таблицы становятся огромными и кодируются длинными числами, что смещает их вниз по списку. Однако для небольшой доли очень больших структур характерна внутренняя элегантная простота, что сильно упрощает их описание. Рассмотрим математическую структуру, элементами которой являются целые числа: 0, 1, 2, 3, …, и отношения сложения и умножения. Было бы напрасной тратой сил выписывать для задания умножения колоссальную таблицу умножения для всех пар чисел: даже если ограничиться первым миллионом чисел, таблица с миллионом строк и миллионом столбцов содержит триллион клеток. Вместо этого мы учим детей лишь таблице умножения первых десяти чисел, а также простому алгоритму, как использовать эту таблицу для умножения многозначных чисел. Для компьютеров мы описываем умножение ещё эффективнее, чем для детей: когда все числа представлены в двоичной системе счисления, нужно задать таблицу умножения размером всего 2 ? 2 для нулей и единиц и добавить короткую компьютерную программу, которая указывает, как пользоваться таблицей для перемножения сколь угодно больших чисел.

Программа хранится просто как конечная строка нулей и единиц (битовая строка), которую можно интерпретировать как целое число, записанное в двоичной системе. Это даёт альтернативный способ кодирования и нумерации математических структур на рис. 12.4: пусть каждая математическая структура представляется числом, битовая строка которого является кратчайшей компьютерной программой, и её функции определяют все отношения в данной структуре. Теперь структуры будут появляться вверху списка, если их просто описать, даже если они огромны по числу своих элементов. Пионеры теории сложности Рэй Соломонофф, Андрей Колмогоров и Грегори Хайтин определили алгоритмическую сложность (для краткости — сложность) битовой строки как длину компьютерной программы, которая выдаёт эту строку. Это означает, что альтернативный основной список перечисляет математические структуры в порядке возрастания сложности.

Замечательная особенность этого нового списка состоит в том, что он также может содержать математические структуры с бесконечным числом элементов. Так, для определения математической структуры из всех целых чисел с операциями сложения и умножения понадобится просто задать кратчайшую программу, которая способна считывать сколь угодно длинные числа, складывать и перемножать их. Такие алгоритмы есть в системе Mathematica и других программных пакетах компьютерной алгебры. Математические структуры, включающие бесконечное множество точек, образующее континуум, подобно пространству-времени, электромагнитным полям и волновым функциям, нередко можно хорошо аппроксимировать конечными структурами, пригодными для компьютерной обработки. Именно так я с коллегами и выполняю большую долю расчётов в области теоретической физики.

Короче говоря, мультиверс IV уровня можно систематически отобразить путём перечисления математических структур с помощью компьютера и изучения их свойств. Если однажды нам удастся определить, в какой математической структуре мы живём, можно будет сослаться на неё по номеру в основном списке, и мы получим возможность записать свой адрес в полной физической реальности (рис. 12.5). Государства применяют разные схемы записи адресов: в одних почтовые индексы состоят из цифр, в других — из букв, а кое-где индексов нет вообще. Аналогично, способ записи локальной части адреса будет зависеть от математической структуры: в большинстве их нет ни квантовой механики, ни инфляции, а значит, нет ни мультиверсов I, II и III уровней, ни планет, хотя другие структуры могут содержать иные типы параллельных вселенных, о которых мы и не догадываемся.

Рис. 12.5. Для задания адреса в полной физической реальности мне понадобится указать своё положение в мультиверсе IV уровня (номер моей математической структуры), в мультиверсе III уровня (ветвь квантовой волновой функции), в мультиверсе II уровня (постинфляционный пузырь), в мультиверсе I уровня (хаббловский объём), а также положение внутри нашей Вселенной. Я привёл здесь небольшие числа, хотя на каждом из четырёх уровней может быть бесконечно много членов, так что в мой реальный адрес будут входить числа слишком большие, чтобы они поместились на конверте.

Структура мультиверса IV уровня

Исследовать мультиверс IV уровня интересно. Если принять популярное формалистическое определение математики как «изучение математических структур», то исследование мультиверса IV уровня окажется тем самым делом, которым занимаются математики. Для физиков вроде меня, признающих гипотезу математической Вселенной, это равносильно исследованию фундаментальной физической реальности и поиску нашего места в ней. Причём исследовать мультиверс IV уровня проще, чем любой нижестоящий мультиверс или даже нашу Вселенную, поскольку для этого не нужны ни ракеты, ни телескопы — достаточно компьютеров и идей. Так что я получил массу удовольствия, создавая компьютерные программы, перечисляющие и классифицирующие математические структуры.

Занимаясь этим на практике, сталкиваешься с ошеломляющей избыточностью. Существует очень много способов написать компьютерную программу, которая выполняет любое вычисление, и столь же огромное число эквивалентных способов описания конечных математических структур с помощью таблиц чисел, соответствующих, например, способам упорядочения или обозначения элементов. В гл. 10 мы упоминали о том, что математическая структура — это класс эквивалентности описаний. Так что каждая математическая структура должна появляться в основном списке всего однажды, причём заданная лишь одним, самым коротким, из множества эквивалентных описаний.

Для любых двух математических структур можно определить новую структуру путём объединения всех элементов двух исходных структур и отношений между ними. Многие структуры в нашем основном списке как раз составные, и при изучении мультиверса IV уровня есть смысл их игнорировать. Это связано с тем, что нет отношений, соединяющих две части, а значит, самосознающий наблюдатель в одной из таких частей никогда не узнает о существовании другой части и не испытает её влияния. Поэтому он может действовать так, будто другой части вовсе не существует либо она не является частью его математической структуры. Единственный случай, при котором составные структуры могут, вероятно, иметь значение, — когда они входят в решение проблемы меры, изменяя вероятности того, что вам выпадет жить в той или иной математической структуре. Поскольку составные структуры описывать гораздо сложнее, они обычно оказываются гораздо дальше в нашем списке, чем их части, и это может придавать им меньшую «меру». На самом деле для любого конечного числа структур мультиверса IV уровня далеко внизу основного списка существует единая составная структура, содержащая их все.

Хотя математические структуры в мультиверсе IV уровня не соединены каким-либо физически осмысленным образом, на метауровне между ними много интересных отношений. Например, мы только что разобрали, как одна структура может быть объединением других. Или: одна структура может в некотором смысле описывать другую. Элементы первой могут соответствовать отношениям во второй, а отношения в первой описывать, что происходит при комбинировании отношений во второй. В этом смысле содержащая 24 отношения структура «повороты куба» (рис. 12.4) описывается структурой, которую математики называют «группа вращений куба». Её 24 элемента соответствуют всем возможным поворотам, сохраняющим идеальный куб внешне неизменным. Множество математических структур обладает симметриями куба и, таким образом, имеет основания считаться кубами — например структуры, элементы которых соответствуют граням, вершинам или рёбрам куба, а отношения указывают, как повороты переупорядочивают эти элементы, либо говорят, какие из них чьими соседями являются.

Ограничения, накладываемые на мультиверс IV уровня: неразрешимость, невычислимость и неопределённость

Насколько велик мультиверс IV уровня? Прежде всего, существует бесконечно много конечных математических структур: их так же бесконечно много, как и чисел: 1, 2, 3, …, поскольку все их можно перечислить в одном пронумерованном списке. Но сколько в мультиверсе IV уровня бесконечных математических структур, где каждая состоит из бесконечного множества элементов? Мы видели, что некоторые бесконечные структуры также могут быть заданы и включены в основной список наряду с конечными структурами за счёт использования компьютерных программ, определяющих их отношения. Однако включение бесконечности вызывает множество онтологических проблем. Чтобы убедиться в этом, рассмотрим математическую структуру, где элементами являются числа 1, 2, 3, …, над которыми определены три отношения (функции) — правила, которые получают на входе числа и определяют новое число согласно следующим определениям:

1. P(n) — для данного числа n, P(n) обозначает наименьшее простое число, большее чем n.

2. T(n) — для данного числа n, T(n) обозначает наименьшее простое число-близнец, большее n (парное простое число — такое, что ближайшее к нему число-близнец отличается от него на 2; примером простых чисел-близнецов служат числа 11 и 13).

3. H(m,n) — для данных двух чисел, m и n, H(m,n) равно 0, если m-ая компьютерная программа в нашем основном списке всех компьютерных программ будет работать бесконечно, если ей на вход подать число n, и H(m, n) равно 1, если, напротив, эта программа завершит работу, сделав конечное число шагов.

Подходит ли эта структура для включения в качестве члена в мультиверс IV уровня, или она недостаточно корректно определена? Первая функция, P(n), совершенно замечательна: нетрудно написать программу, которая начинает проверять, являются ли следующие за n числа простыми, и останавливается, как только находит такое. У нас есть гарантия, что эта программа остановится после конечного числа шагов, поскольку известно, что существует бесконечно много простых чисел (это доказал ещё Евклид). Так что P(n) — пример вычислимой функции.

Вторая функция, T(n), хитрее. Легко написать программу, которая проверяет каждое число, следующее за n, на предмет того, не является ли оно простым-близнецом. Но если подставить число n больше, чем 37 568 016 956 852^666 669 —1 (это самое большое простое число-близнец, известное сейчас), то нет гарантии, что программа когда-нибудь остановится и даст ответ. Несмотря на все усилия математиков, мы до сих пор не знаем, бесконечно ли количество простых чисел-близнецов. Так что мы не знаем, является ли T(n) вычислимой, а значит, и строго определённой функцией. Таким образом, остаётся под вопросом, можно ли математическую структуру, содержащую такое неаккуратно заданное отношение, считать корректно определённой.

Третья функция, H(m,n), ещё более скверная: пионеры кибернетики Алонзо Чёрч и Алан Тьюринг установили, что не существует программы, которая могла бы вычислить H(m, n) для произвольных аргументов m и n за конечное число шагов, так что H(m,n) — это пример невычислимой функции. Иными словами, не существует программы, способной определять, какие из других программ в конце концов остановятся. Конечно, любая программа либо остановится, либо нет, но хитрость в том, что, как и в случае с простыми числами-близнецами, вам, возможно, понадобится ждать окончания расчётов вечно. Открытие Черчем и Тьюрингом невычислимых функций тесно связано с открытием логиком Куртом Гёделем того факта, что некоторые арифметические теоремы неразрешимы, то есть их нельзя ни доказать, ни опровергнуть за конечное число шагов.

Следует ли рассматривать математические структуры как корректно определённые, даже если они содержат такие отношения, как H, которые нельзя вычислить и на сколь угодно мощном компьютере? Если да, то такая структура может быть известна лишь подобной оракулу сущности, которая способна реально выполнить бесконечное число вычислительных шагов, необходимых для получения ответа. Такие структуры никогда не появятся в обсуждавшемся выше основном списке: он учитывает лишь структуры, определимые с помощью обычных компьютерных программ, а не при участии всемогущего оракула.

Наконец, рассмотрим одну из самых популярных математических структур нашего времени — вещественные числа (наподобие 3,141 592…, где последовательность десятичных цифр тянется до бесконечности). Они образуют континуум, и для задания даже одного произвольного такого числа потребуется список из бесконечного числа цифр, то есть бесконечное количество информации. Это означает, что обычные компьютерные программы не способны обрабатывать такие числа: проблема касается не только выполнения бесконечного числа вычислительных шагов, как в примере с функцией H, но также ввода и вывода бесконечного количества информации.

С другой стороны, работа Гёделя может вызвать беспокойство: не лишена ли смысла ГМВ в применении к бесконечным структурам? Наша Вселенная тогда оказалась бы в некотором смысле противоречивой или неопределённой. Если принять тезис математика Давида Гильберта о том, что «математическое существование сводится, по сути, к отсутствию противоречий», то внутренне противоречивая структура не существует математически, не говоря уже о физическом существовании, как в ГМВ. Стандартная модель физики включает такие повседневно применяемые математические структуры, как целые и вещественные числа. Тем не менее работа Гёделя оставляет открытыми вопросы, не является ли повседневная математика внутренне противоречивой и не существует ли в рамках теории чисел доказательства конечной длины, демонстрирующего, что 0 = 1. На основе такого шокирующего результата можно было бы доказать, что любое синтаксически корректное утверждение о целых числах является истинным, и математика в том виде, как мы её знаем, обрушилась бы, подобно карточному домику.

Подобные сомнения относительно неразрешимости и внутренней противоречивости применимы лишь к математическим структурам, содержащим бесконечно много элементов. Присущи ли бесконечности, неразрешимости и потенциальные внутренние противоречия непосредственно фундаментальной физической реальности? Или это, по сути, миражи, артефакты, возникающие в результате нашей игры с огнём и применения мощных математических инструментов, которые скорее более удобны в использовании, нежели подходят для фактического описания нашей Вселенной? То есть — насколько корректно определёнными должны быть математические структуры, чтобы быть реальными, выступать членами мультиверса IV уровня?

Есть целый спектр интересных возможностей для квалификации структур:

Гипотеза вычислимой Вселенной

Интересные возможности предоставляет нам гипотеза вычислимой Вселенной (ГВВ). Она состоит в том, чтобы провести границу по варианту № 3 и дисквалифицировать структуры более общего вида:

Я имею в виду следующее: все отношения (функции), которые определяют математическую структуру, могут быть реализованы как вычисления, которые гарантированно останавливаются после конечного числа шагов. Если ГВВ неверна, то ещё более консервативной гипотезой является гипотеза финитной Вселенной (ГФВ). Она проводит границу по варианту № 2: наша внешняя реальность является финитной математической структурой.

Мне кажется интересным, что очень близкие вопросы дебатировались среди математиков без ссылок на физику. Согласно финитистской школе математиков, к которой принадлежали Леопольд Кронекер, Герман Вейль и Рубен Гудстейн, математический объект не существует, если его нельзя построить из целых чисел за конечное число шагов. Это ведёт прямо к варианту № 3.

Согласно ГВВ, математическая структура, которая является нашей физической реальностью, обладает привлекательным свойством вычислимости, а значит, является корректно определённой в строгом смысле (то есть все её отношения могут быть вычислены). Таким образом, у нашей Вселенной не может быть никаких невычислимых (неразрешимых) физических особенностей, а значит, можно не беспокоиться, что работы Чёрча, Тьюринга и Гёделя каким-то образом сделают наш мир неполным или внутренне противоречивым. Я не знаю точно, каковы свойства нашей физической реальности, но уверен, что эти свойства существуют в том смысле, что они корректно определены: природа наверняка знает, что делает.

Многих авторов озадачивало, почему наши физические законы выглядят относительно просто. Например, почему Стандартная модель физики элементарных частиц обладает такими простыми симметриями, которые мы обозначаем как SU(3) ? SU(2) ? U(1), и требует всего 32 параметра (гл. 10), тогда как большинство альтернатив значительно сложнее её? Очень соблазнительно думать о том, что свой вклад в эту простоту внесла ГВВ, которая строго ограничивает сложность природы. Может быть, изгнав континуум, ГВВ также поможет уменьшить размер инфляционного ландшафта и разрешить космологическую проблему меры? Она в значительной мере связана с возможностью истинного континуума вечно испытывать экспоненциальное расширение, порождая бесконечное число наблюдателей.

Это были хорошие новости. Однако, хотя ГВВ имеет привлекательные черты, гарантирующие строгую определённость нашей Вселенной и, возможно, снижающие остроту космологической проблемы меры за счёт ограничения того, что считается существующим, она также приводит к серьёзным вызовам.

Прежде всего меня беспокоит, что ГВВ кажется сдачей важных философских высот, так как, по сути, она признаёт: хотя где-то существуют все математические структуры, некоторые из них обладают привилегированным статусом. Но если ГВВ верна, то все остальные математические ландшафты являются, по большому счёту, иллюзиями, фундаментально неопределёнными и в любом смысле несуществующими.

Более насущной является та проблема, что наша нынешняя Стандартная модель (как и все исторически успешные теории) нарушает ГВВ, и совершенно неочевидно, что существует жизнеспособная вычислимая альтернатива. Главная причина нарушения ГВВ состоит в использовании континуума, обычно в форме вещественных и комплексных чисел. Они не могут служить даже исходными данными для финитных вычислений, поскольку в общем случае требуют для своего задания бесконечно много битов. Даже те подходы, в рамках которых предпринимается попытка избавиться от классического континуума пространства-времени путём дискретизации или квантования, обычно применяют непрерывные переменные для других элементов теории, таких как напряжённость электромагнитного поля или амплитуда квантовой волновой функции.

Один из интересных подходов к проблеме континуума состоит в замене вещественных чисел математической структурой, которая имитирует континуум, сохраняя вычислимость, — например алгебраическими числами. Другой подход (он кажется мне перспективнее) состоит в том, чтобы перестать рассматривать континуум в качестве фундаментальной структуры и попробовать относиться к нему как к аппроксимации. Я уже отмечал, что физики никогда ничего не измеряли с точностью более 16 значащих цифр, и нет эксперимента, исход которого зависел бы от гипотезы существования истинного континуума или от способности природы вычислять нечто невычислимое. Поразительно, но многие основанные на континууме модели классической математической физики (например уравнения, описывающие волны, диффузию или течение жидкости) являются не более чем аппроксимацией лежащего в основе поведения совокупностей дискретных атомов. Исследования в области квантовой гравитации указывают на то, что даже классическое пространство-время на очень малых масштабах распадается. Таким образом, нет уверенности, что величины, с которыми мы обращаемся как с непрерывными (вроде пространства-времени, напряжённости поля, амплитуды квантовой волновой функции), не являются лишь аппроксимациями чего-то дискретного. На самом деле некоторые дискретные вычислимые структуры (и даже финитные, удовлетворяющие ГФВ) могут аппроксимировать континуальную физическую модель настолько хорошо, что физики применяют их, когда нужно выполнить практические вычисления, оставляя открытым вопрос о том, что ближе к математической структуре Вселенной — первое или второе. Некоторые исследователи, например Конрад Цузе, Джон Барроу, Юрген Шмидхубер и Стивен Вольфрам, зашли по этому пути настолько далеко, что предполагают и вычислимость, и финитность законов природы, подобно клеточным автоматам или компьютерным моделям. Отмечу, однако, что эти предположения отличаются от ГВВ и ГФВ тем, что требуют вычислимости эволюции во времени, а не просто описания (отношений) структуры.

Ещё один поворот. Физики нашли примеры того, как нечто непрерывное (вроде квантовых полей) может порождать дискретное решение (вроде кристаллической решётки), которая, в свою очередь, кажется похожей на непрерывную среду в больших масштабах, и при этом подвержена колебаниям, которые ведут себя как дискретные частицы, называемые фононами. Мой коллега из МТИ Вэнь Сяоган показал, что «эмерджентные» частицы могут даже вести себя, как частицы в нашей Стандартной модели. Это открывает возможность существования множества слоёв эффективно непрерывных и дискретных описаний, надстроенных над дискретной вычислимой структурой в основании.

Трансцендентная структура IV уровня

Выше мы рассмотрели тесную взаимосвязь математических структур с вычислениями, при которой первые определяются вторыми. С другой стороны, вычисления — не более чем частный случай математических структур. Так, информационное содержание (состояние памяти) цифрового компьютера — эта строка битов (скажем, 1 001 011 100 111 001…) большой, но конечной длины, эквивалентная некоему большому, но конечному целому числу n, записанному в двоичной системе. Обработка информации в компьютере — это детерминистическое правило изменения каждого состояния памяти на другое (применяемое снова и снова). Так что математически это просто отображающая целые числа на себя функция f, которая многократно применяется: n f(n) f(f(n)) … Иными словами, даже самая сложная компьютерная модель — это не более чем частный случай математической структуры, а значит, она включается в мультиверс IV уровня.

На рис. 12.6 показано, как вычисления и математические структуры связаны не только друг с другом, но также с формальными системами — абстрактными символическими системами аксиом и правил вывода, которые математики применяют для доказательства теорем о математических структурах. Прямоугольники на рис. 12.1 соответствуют таким формальным системам. Если формальная система описывает математическую структуру, то говорят, что последняя является моделью первой. Более того, вычисления могут порождать теоремы в формальных системах (для некоторых классов формальных систем существуют алгоритмы, способные вычислить все теоремы).

На рис. 12.6 также показано, что во всех трёх вершинах треугольника потенциально существуют проблемы: отношения в математических структурах могут быть неопределёнными, формальные системы могут содержать неразрешимые утверждения, а вычисления могут не останавливаться после конечного количества шагов. Отношения между тремя вершинами и соответствующими трудностями обозначены шестью стрелками, смысл которых я подробно объяснил в статье 2007 года о математической Вселенной. Поскольку разные стрелки изучаются специалистами из разных областей — от математической логики до информатики, — исследование этого треугольника как целого является междисциплинарным. Я думаю, оно заслуживает большего внимания.

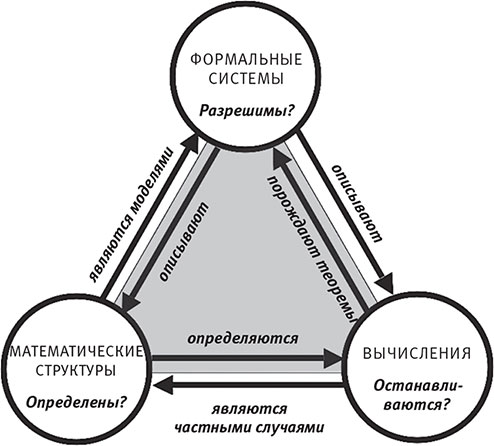
Рис. 12.6. Стрелки обозначают тесные взаимосвязи между математическими структурами, формальными системами и вычислениями. Вопросительный знак указывает на то, что всё это аспекты одной трансцендентной структуры, природу которой мы до конца пока не понимаем.

В центре треугольника я поставил вопросительный знак. Он указывает на предположение, что три вершины (математические структуры, формальные системы и вычисления) являются просто аспектами одной лежащей в основе трансцендентной структуры, природу которой мы пока понимаем не до конца. Эта структура — возможно, ограниченная до определённой (разрешимой, останавливающейся) части, как в ГВВ, существует где-то в свободном от «багажа» виде и являет собой всю полноту математического и физического существования.