Книга: Как работает Вселенная: Введение в современную космологию
2.7.3. Параметр замедления
| <<< Назад 2.7.2. Исследование решений |
Вперед >>> 2.7.4. Материя с ненулевым давлением в расширяющейся Вселенной |
2.7.3. Параметр замедления

Некоторые полезные величины могут быть получены без каких-либо дифференциальных уравнений типа (2.12). Параметр замедления в космологии определяется как[35]

Здесь точка над переменной означает ее производную по времени, а две точки – вторую производную по времени. Таким образом,


Мы можем определить эту величину, использовав формулу для ускорения частицы на поверхности сферы

Параметр замедления равен
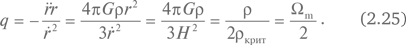
Здесь ?m = ?/?крит – параметр плотности материи. Можно убедиться, что расширение действительно замедляется и параметр замедления q равен 0,5 для плоской модели, превышает 0,5 для закрытой модели и находится в интервале от 0 до 0,5 для открытой модели.
Из уравнений (2.10) и (2.11) также следует, что

Ранее мы встречались с этой же формулой, но примененной к текущему моменту времени (2.15).
Обратите внимание, что из закона Хаббла (2.1) следует

что означает, что

Таким образом, замедление означает не только уменьшение Н, оно означает, что qположительно и

| <<< Назад 2.7.2. Исследование решений |
Вперед >>> 2.7.4. Материя с ненулевым давлением в расширяющейся Вселенной |
- 2.6.1. Параметр замедления
- 3.3. Связь устойчивости атмосферы с погодными условиями и метеорологическими параметрами
- 3.2. Параметры расширения струй и клубов
- 1.5. Определяющие параметры физико-математических моделей
- Взаимосвязь между эволюционными и фенотипическими параметрами, универсалии эволюции генов, белков и геномов и физическая...
- Таблица 4.5. Параметры семейств околосолнечных комет [Knight, 2008]
- 4.4. Орбитальные параметры комет
- Таблица 10.6. Параметры астероидоцентрического движения КА
- Таблица 10.5. Основные параметры Апофиса
- Главный параметр
- 10.5. Предпочитаемые параметры тела
- Множественные параметры
