Книга: Большое космическое путешествие

Глава 18 Следствия специальной теории относительности

Глава 18

Следствия специальной теории относительности

Автор: Дж. Ричард Готт

Специальная теория относительности Эйнштейна произвела революцию в научных представлениях о пространстве и времени. Эта теория подразумевала, что время можно трактовать как четвертое измерение наряду с тремя пространственными измерениями. Интересно, что учитель Эйнштейна Герман Минковский воспользовался его работами о теории относительности и на их основе разработал свою геометрическую картину пространства и времени, опубликовав результаты работы в 1907 году. Эйнштейн сразу же согласился с его точкой зрения. Мы живем в четырехмерной Вселенной. Что это означает? Принято считать, что поверхность Земли двумерная. Чтобы обозначить любую точку на поверхности Земли, нужны две координаты: широта и долгота. Если вы знаете широту и долготу, то знаете, в какой точке Земли находитесь. Но Вселенная четырехмерна, а значит, чтобы указать местоположение во Вселенной, нужны четыре координаты. Если я хочу, чтобы вы пришли на вечеринку, то должен буду вам сообщить значения широты и долготы, под которыми она состоится, но еще должен сообщить и высоту. Вам же не нужно на четвертый этаж, если вечеринка будет на двенадцатом! Кроме того, я должен сказать вам, к какому времени прийти. Если вы придете не вовремя, то пропустите вечеринку, точно как если бы зашли не на тот этаж. Любое событие, например новогодние посиделки на 54-м этаже в здании, расположенном на пересечении 5-й авеню и 34-й улицы в Нью-Йорке, описывается четырьмя координатами: широтой, долготой, высотой над поверхностью земли и временем, к которому нужно прибыть. Поскольку для этого нужны четыре координаты, нам известно, что мы живем в четырехмерной Вселенной.

Вооружившись этой идеей, можно чертить пространственно-временные схемы. Несомненно, вы видели картинку, на которой Земля обращается вокруг Солнца. Солнце – большой белый круг в центре, а орбита Земли показана как прерывистая окружность вокруг него (поскольку эллиптическая земная орбита по форме очень близка к круговой). Землю можно изобразить как маленькую голубую точку, причем если сопоставить картинку с циферблатом, то 1 января точка Земли окажется на 12 часах. Если бы мы хотели показать, как Земля движется вокруг Солнца, то сделали бы последовательность картинок, и на них Земля двигалась бы по орбите против часовой стрелки. 1 февраля она оказалась бы на отметке 11 часов, 1 марта – на 10 часов и так далее. Вращение Земли можно изобразить в виде мультфильма: проматывая кадры, мы видим, как Земля совершает путь вокруг Солнца.

Теперь предположим, что мы взяли этот мультфильм и разрезали на отдельные кадры, а получившиеся фрагменты сложили в стопку друг на друга. Каждый кадр соответствует моменту времени, и чем выше кадр лежит в стопке, тем более поздний момент обозначает. Таким образом мы могли бы дать пространственно-временную картину вращения Земли вокруг Солнца. Ось времени пройдет по вертикали: прошлое будет находиться снизу, а будущее – сверху. Две горизонтальные линии соответствуют двум пространственным измерениям (изображаемым на двумерной модели орбитального вращения Земли вокруг Солнца). Солнце не движется, оно всегда в центре, и, следовательно, все солнечные круги складываются в «полосу», пронизывающую стопку кадров по вертикали. Но Земля в каждом кадре переходит на новое место, продолжая движение по околосолнечной орбите против часовой стрелки. Поэтому орбита Земли напоминает голубую спираль, вьющуюся вокруг центральной белой точки (Солнца). Радиус голубой спирали равен 8 световым минутам – это радиус земной орбиты. Спираль ежегодно оборачивается вокруг Солнца по вертикали. Голубая спираль, вьющаяся вокруг вертикальной белой колонки, – это пространственно-временная схема. На эту схему можно добавить орбиты Меркурия, Венеры и Марса, которые будут выглядеть как новые спирали, также вьющиеся вокруг белой колонки (Солнца). Это трехмерная схема, но я убираю одно из пространственных измерений, чтобы ее можно было визуализировать. В четырехмерном виде эту схему никак нельзя было бы визуализировать – в любом случае получилось бы не более трех измерений. В этой книге мы изобразили схему в трех измерениях, воспользовавшись стереопарой картинок (рис. 18.1). Можете полюбоваться этой иллюстрацией либо как парой фотографий, либо как трехмерной моделью, где обе картинки показаны в немного разных ракурсах. Чтобы увидеть эту картинку объемной, во всем ее великолепии, вернитесь к врезке рядом с рис. 4.2 и посмотрите на рис. 18.1, как там описано.

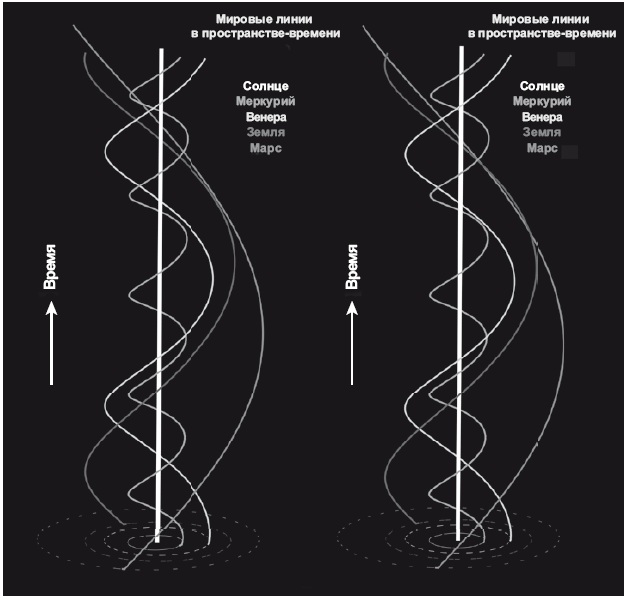
Рис. 18.1. Пространственно-временная схема внутренней части Солнечной системы. Время откладывается по вертикали, а два пространственных измерения – по горизонтали. Это объемное изображение, две картинки можно рассматривать как стереопару. О том, как правильно смотреть такие картинки, рассказано в пояснении к рис. 4.2. Мировая линия Солнца – это вертикальная белая полоса, идущая посередине. Земля вращается вокруг Солнца против часовой стрелки, поэтому ее мировая линия сначала проходит перед линией Солнца, а потом – за ней (выше на этой схеме). Чем дальше планета (Меркурий, Венера, Земля, Марс) от Солнца, тем больше ее сидерический период и, следовательно, тем менее плотную спираль она описывает. Иллюстрация предоставлена Robert J. Vanderbei и J. Richard Gott

Белая вертикальная полоса называется мировой линией Солнца – это путь Солнца в пространстве и времени. Она белая, поскольку само Солнце белое, а не желтое, – об этом мы говорили в главе 4. Голубая спираль – это мировая линия Земли, ее путь в пространстве и во времени. Обратите внимание, как голубая спираль проходит то перед вертикальной линией Солнца, то за ней. Оранжевая спираль, плотно обвивающая вокруг Солнца, – это мировая линия Меркурия. Он совершает оборот вокруг Солнца за 88 дней. Серая спираль соответствует Венере, а красная – Марсу. Если представить Землю в четырех измерениях, то она будет похожа не на шар, а на длинную макаронину, закрученную вокруг Солнца в виде спирали. Земля обладает протяженностью во времени.

У вас тоже есть мировая линия. Она начинается при рождении, проходит через все события вашей жизни и заканчивается со смертью. Толщина вашей мировой линии – сантиметров тридцать, ширина – сантиметров шестьдесят, высота – примерно метр восемьдесят, а продлится она лет восемьдесят, если вам повезет. В пространственно-временных схемах неподвижные мировые линии сплетаются, образуя четырехмерное изваяние.

Можно начертить пространственно-временные диаграммы отдельных мысленных экспериментов, при помощи которых Эйнштейн пытался проиллюстрировать феномен одновременности. Допустим, я сижу у себя в лаборатории, ее ширина – 9 метров. Я землянин. Моя лаборатория неподвижна относительно Земли, а я неподвижно сижу в центре лаборатории. В пространственно-временной схеме координата по оси абсцисс соответствует пространству, а координата по оси ординат – времени. Поскольку я двигаюсь вперед во времени, но не в пространстве (то есть не перемещаюсь ни влево, ни вправо), моя мировая линия растет вверх. Моя лаборатория, ее передняя и задняя стена, также никуда не движется, и мировая линия лаборатории тоже растет вверх. Задняя стена лаборатории, землянин (я) и передняя стена лаборатории образуют три параллельные мировые линии. Будущее вверху, прошлое – внизу. Мировая линия передней стены лаборатории показана по вертикали справа, а мировая линия задней стены лаборатории – по вертикали слева. Шкала по горизонтали откладывается в футах, а по вертикали – в наносекундах. Свет в вакууме преодолевает один фут за наносекунду. На схеме с рис. 18.2 лучи света – это диагональные линии, отклоненные от вертикали на 45°.

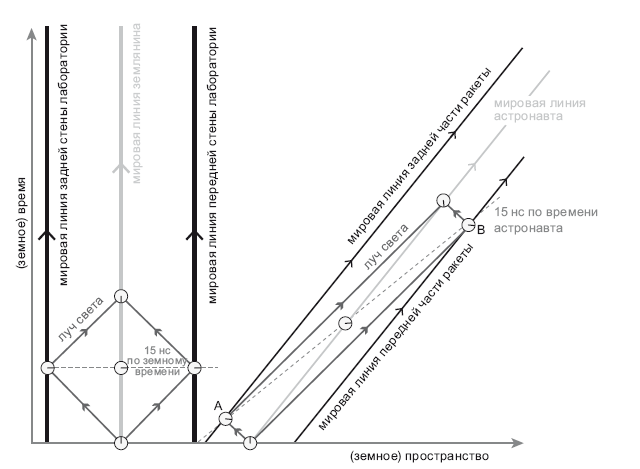
Рис. 18.2. Пространственно-временная схема с мировыми линиями моей лаборатории и ракеты, в которой летит астронавт. Иллюстрация предоставлена Дж. Ричардом Готтом, по образцу из его книги Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

Допустим, в момент t = 0 (земное время ET; на моем рисунке обозначено часиками, стрелка которых указывает вверх) я посылаю два лазерных луча, один вправо, другой влево, и они отражаются соответственно от передней и задней стены моей лаборатории. Мировые линии двух этих лучей света – диагонали, отклоненные от вертикали на 45°. Они одновременно достигают один передней стены лаборатории, другой – задней (оба проходят одинаковое расстояние по 4,5 м), каждый за 15 нс по земному времени. На рисунке показаны двое часиков с циферблатами по 60 нс, стрелка у обоих часов стоит на отметке 15 нс; часы расположены в тех точках, где лазерные лучи попадают соответственно в переднюю и заднюю стенку лаборатории. Мировая линия землянина (моя) также снабжена часиками, стрелка которых стоит на отметке 15 нс (земное время). Трое этих часов, каждые из которых показывают 15 нс, соединены прерывистыми линиями. С моей точки зрения, эта линия соединяет одновременные события. После того как лазерные лучи отразятся от зеркал, подвешенных на передней и задней стене лаборатории, эти лучи вернутся ко мне. Оба вернутся одновременно, спустя 30 нс после старта. Когда лазерные лучи вернутся ко мне, на моих часах будет значиться 30 нс, поскольку эти лучи, летящие со скоростью света, проделали путь 4,5 м туда и 4,5 м обратно, всего по 9 м за 30 нс. Пока все понятно.

Но затем, следуя логике Эйнштейна, рассмотрим, что будет происходить с астронавтом, летящим в ракете со скоростью, равной 80 % скорости света (слева направо). В таком случае мировая линия астронавта должна располагаться под наклоном. Каждые 120 см, которые он проходит вправо, соответствуют 5 нс вверх по оси времени. Он летит с 4/5 (или 80 %) скорости света. И нос, и хвост его ракеты движутся с одинаковой скоростью, и уклон их мировых линий одинаков. Мировая линия носа ракеты, мировая линия астронавта и мировая линия хвоста ракеты параллельны. Они не движутся друг относительно друга. Теперь астронавт сидит в центральной части ракеты и светит лазером в ее переднюю и заднюю часть, точно как я делал в лаборатории. Я измеряю длину его ракеты, получается 540 см. Подробнее я расскажу об этом ниже. Лазерный луч, летящий влево, попадает в корпус ракеты примерно через 270 см (это половина от 540 см). Я наблюдаю за этим экспериментом через иллюминатор ракеты. Вижу, что хвост ракеты за 5 нс смещается вправо на 120 см, а лазерный луч за те же 5 нс успевает пролететь 150 см влево. Итак, 120 см плюс 150 см равно 270 см, так что лазер астронавта попадает в хвост ракеты через 5 нс, покрывая это исходное расстояние (270 см). По моим (земным) часам лазерный луч долетает до хвоста ракеты за 5 нс. Лазерный луч летит влево, а ракета летит вправо, поэтому (с моей точки зрения) лазерный луч и хвост ракеты движутся навстречу друг другу. Тогда как на Земле лазерный луч преодолевает 1350 см за 45 нс (второй постулат Эйнштейна: свет летит со скоростью 30 см/нс), нос ракеты за то же время преодолевает всего 1080 см (4/5 от 1350 см). За 45 нс лазерный луч преодолевает 1350 см, а ракета – всего 1080 см, то есть на 270 см меньше, но у носа ракеты уже есть «фора» в 270 см. Соответственно по «земному» времени лазерный луч попадет в нос ракеты с запаздыванием в 45 нс. Это означает, что, с моей точки зрения, лазерный луч, летящий в хвост ракеты, достигнет цели раньше, чем другой лазерный луч, направленный в нос ракеты. Для меня попадание лазерных лучей в нос и в хвост ракеты – это не одновременные события.

Что же видит астронавт? Он движется с постоянной скоростью в одном и том же направлении; по первому постулату Эйнштейна, астронавт должен полагать, что находится в состоянии покоя. Он сидит в центральной части ракеты, которая относительно него также не движется, и светит лазером в носовую и в хвостовую часть ракеты. Поскольку он сидит в центре ракеты и ракета относительно него не движется, он полагает, что два лазерных луча, летящих со скоростью света, должны за равное время попасть соответственно в нос и в хвост ракеты. С его точки зрения, он должен увидеть два одновременных события: попадание лазерного луча в нос ракеты и попадание другого лазерного луча в хвост ракеты. Я (землянин) не считаю два этих события одновременными: сначала я вижу, как лазер попадает в хвост ракеты, а затем – как другой лазерный луч попадает в нос ракеты. Мы с астронавтом не сойдемся во мнении о том, какие события одновременны, а какие – нет. Это противоречит здравому смыслу, но непосредственно следует из постулатов специальной теории относительности.

Интересно, что когда сам Эйнштейн сформулировал этот мысленный эксперимент, он говорил не об астронавте на ракете, в носовой и хвостовой части которой установлены два зеркала, а о пассажире поезда, причем два зеркала были установлены в голове и хвосте поезда. В 1905 году самым быстрым транспортным средством был поезд – он развивал скорость под 200 км/ч!

Для нас с астронавтом пространство-время сегментируется по-разному. Представьте себе, что пространство-время похоже на четырехмерную буханку хлеба. В Америке буханка похожа на кирпичик, так что ее можно поставить на один конец и нарезать горизонтальными ломтиками. Каждый из этих ломтиков будет соответствовать одному мгновению земного времени (ET), и в каждом ломтике содержатся события, которые с моей точки зрения происходят одновременно. Астронавт нарезает пространство-время иначе. Он (назовем его Жак) нарезает хлеб, как это принято во Франции – под углом. Его скошенные ломтики соответствуют моментам «астронавтского» времени (AT). Мы с Жаком не сможем сойтись во мнении о том, какие события одновременны, то есть какие события лежат в одном и том же ломтике. Мы с ним нарезаем буханку по-разному, но видим одну и ту же буханку. По Эйнштейну, реальны те феномены, которые не зависят от наблюдателя. Пространство и время не существуют в отдельности друг от друга. Я считаю, что настоящее – это ломтик обычной буханки-кирпичика, а для Жака настоящее – это ломтик скошенной набок французской буханки. Поскольку Жак движется относительно меня, мы не сможем прийти к общему мнению о том, что есть настоящее. Соответственно мы по-разному будем относить события к прошлому и к будущему. Но у нас не возникнет споров относительно пространственно-временной буханки. Это четырехмерное пространство-время, и оно реально.

Теперь вернемся к тому, какой мне представляется ракета Жака. После того как лазерный луч Жака отразится от зеркала в носовой части ракеты, он вернется к Жаку всего через 5 нс (с моей точки зрения). Я вижу, как лазерный луч и астронавт приближаются друг к другу. Всего за 5 нс отраженный лазерный луч успевает пролететь 150 см, а ракета за то же время пролетает 120 см, таким образом, за 5 нс астронавт и лазерный луч сближаются на 270 см. С моей точки зрения, лазерный луч, отправленный в носовую часть ракеты, за 50 нс успевает слетать туда и обратно (45 нс + 5 нс). Лазерный луч, отправленный в заднее зеркало, догоняет астронавта за 45 нс. По земному времени (ET) ему на это нужно 5 + 45 нс. Соответственно с моей точки зрения оба лазерных луча возвращаются к астронавту одновременно. Астронавту также должно казаться, что отраженные лучи возвращаются к нему одновременно, так как они возвращаются в неизменных пространственно-временных координатах.

У меня на часах между пуском и возвращением двух лазерных лучей проходит 50 нс. Я вижу, как лазерные лучи движутся на скорости 80 % от скорости света (v/c = 0,8), поэтому мне должно казаться, что часы астронавта идут с 60-процентной скоростью (или ?1 – (v²/c²)) по сравнению с моими часами. За то время, пока на моих часах пройдет 50 нс, астронавт должен состариться всего на 30 нс. Когда астронавт фиксирует возврат лазерных лучей, он должен сказать, что они вернулись за 30 нс «астронавтского» времени (AT), поскольку к моменту их прибытия он состарится на 30 нс. Лазерные лучи должны были одновременно достичь носа и хвоста ракеты через 15 нс AT после пуска. Обратите внимание на ломоть французской буханки, на котором написано «15 нс AT». С точки зрения астронавта, в этом ломте находятся одновременные события. Астронавту кажется, что он находится в состоянии покоя, и вся ситуация выглядит для него точно так же, как выглядела бы для меня в лаборатории на Земле. Поскольку по его времени лазерные лучи успевают обернуться за 30 нс, он должен логически заключить, что длина ракеты – 9 м.

Два события – попадание лазерных лучей в хвостовую и носовую часть ракеты – кажутся мне отдельными актами, разделенными в пространстве на 15 м и во времени на 45 нс. Если воспользоваться скоростью света (30 см/нс) для сравнения расстояний в пространстве и расстояний во времени, то можно сказать, что для меня эти события будут разделены в пространстве сильнее, чем во времени. Такой феномен называется «пространственноподобным интервалом». Обязательно найдется астронавт, летящий с огромной скоростью (которая, однако, ниже световой), кому два этих события покажутся одновременными. Ему покажется, что эти события разделены в пространстве, но происходят одновременно. Эйнштейн продемонстрировал, что два наблюдателя могут прийти к общему мнению лишь о том, чему равен квадрат интервала между двумя событиями в пространстве минус квадрат интервала между этими же событиями во времени; обозначим эту величину ds². Выбрав систему отсчета, в которой скорость света равна единице (то есть 30 см = 1 нс), я нахожу, что два события должны быть разделены в пространстве на 50 единиц и во времени на 40 единиц. В таком случае я могу вычислить ds2 = 50²–40² = 2500–1600 = 900. Но астронавт Жак считает, что два этих события произошли одновременно и они разделены в пространстве на 30 единиц (как вы помните, он считает, что длина его ракеты 9 м). Но когда он вычисляет ds², у него получается 30² – 0², или 900, точно как у меня. Мы можем не сойтись в вопросах о времени и расстоянии, но, как ни удивительно, некоторые важные феномены остаются для нас тождественными.

Теперь рассмотрим интервал между тем моментом, когда астронавт отправляет световой сигнал, и моментом прибытия этого сигнала в хвост ракеты. Измеряемая мною в пространстве дистанция между двумя этими событиями составит 150 см, а временной интервал между двумя этими событиями – 5 нс. Итак, можно вычислить, что ds² равен (интервал в пространстве)² – (интервал во времени)² равен 5²–5² = 0. По измерениям астронавта, точки двух событий отстоят друг от друга на 150 см и между этими событиями проходит 5 нс. Таким образом, у него получается 15²–15² = 0, точно как и у меня. События, соединенные лучом света (в таком случае говорят о нулевом интервале), всегда имеют ds² = 0 с точки зрения любого наблюдателя. Согласно второму постулату Эйнштейна, все наблюдатели должны видеть луч света, летящий в этой системе координат с постоянной скоростью 1 (30 см/нс); следовательно, интервал в пространстве должен быть равен интервалу во времени и ds² должно быть равно нулю. На самом деле, знак «минус» в формуле ds² нужен для того, чтобы гарантировать, что второй постулат всегда выполняется.

По теореме Пифагора, если в плоскости с системой декартовых координат (x, y) две точки разделены отрезками dx и dy, то их (интервал в пространстве)² = dx² + dy² + dz². Это евклидова стереометрия, изучаемая в старших классах. Но Эйнштейн утверждает, что ds² = (интервал в пространстве)2 – (интервал во времени)². Эту формулу можно переписать в виде ds² = dx² + dy² + dz²– (интервал во времени)2. Но интервал во времени равен просто dt. Итак, подставив это значение, имеем ds² = dx² + dy² + dz² – dt². Так что есть разница между временным измерением t и любым из пространственных измерений (x, или y, или z): перед dt² стоит знак «минус». В этом минусике и есть вся разница. Именно он отличает время от известных нам обычных пространственных измерений.

Уф! Мы изрядно позанимались арифметикой, но подходим к важному моменту: разнице между временем и пространственными измерениями.

Как вы помните, в самом начале я измерил длину ракеты астронавта, и у меня получилось 540 см. Таким образом, ракета короче, чем кажется астронавту (он считает, что ее длина 9 м). Таким образом, мне его ракета кажется в ?1 – (v²/c²) раз короче, чем ему. Наши часы рассогласованы, наши рулетки рассогласованы – что, опять же, подтверждает, что наблюдаемая скорость света всегда равна 30 см/нс. Как могут разниться наши данные о ширине мировой линии его ракеты? Дело в том, что «ломтики» пространства-времени, приходящиеся на эту мировую линию, у нас отличаются. Я измеряю ширину мировой линии в конкретный момент земного времени (ET), а он – в конкретный момент ракетного времени (AT). Я режу его мировую линию горизонтальными ломтиками, как обычную американскую буханку, а он режет ее под углом, как французский хлеб. Другая метафора: допустим, я распилил ствол дерева по горизонтали и говорю: «Ширина ствола – 15 см». Если бы кто-то распилил этот же ствол наискосок, то у него мог бы получиться спил шириной 25 см, хотя ствол был бы тот же самый. Мы с астронавтом просто по-разному режем мировую линию ракеты.

Почему это важно? Рассмотрим крайний случай, когда астронавт летит мимо меня (я на Земле) со скоростью 99,995 % от скорости света; в такой ситуации волшебный коэффициент ?1 – (v²/c²) равен 1/100. Я вижу, что астронавт направляется к звезде Бетельгейзе, до которой 500 световых лет. На мой взгляд, он прибудет туда примерно через 500 лет: ведь он летит практически со скоростью света, а до Бетельгейзе 500 световых лет, так что пока он туда доберется, на Земле пройдет 500 лет (ET). Но я увижу, что он состарился всего на 1/100 ? 500 лет – на 5 лет. Мне кажется, что его часы идут очень медленно, именно потому, что он летит так быстро. Все его действия кажутся мне медленными – пока он позавтракает, у меня на часах пройдет пятеро суток! Достигнув Бетельгейзе, он действительно состарится всего на 5 лет.

Как он сам воспринимает этот путь? Ему кажется, что он находится в покое, Земля удаляется от него со скоростью 99,995 % от скорости света, а Бетельгейзе – приближается с такой же скоростью. Сначала он видит, как мимо пролетает Земля – вжух! – потом, 5 лет спустя, как мимо пролетает Бетельгейзе – вжух! В принципе, Земля и Бетельгейзе находятся в состоянии покоя друг относительно друга, их мировые линии параллельны. Система Земля + Бетельгейзе для астронавта подобна огромной ракете, на носу которой расположена Земля, а в хвосте – Бетельгейзе. Поскольку эта ракета пролетает мимо него практически со скоростью света, то есть расстояние от Земли до Бетельгейзе преодолевается за 5 лет, астронавт приходит к выводу, что длина ракеты Земля – Бетельгейзе равна 5 световых лет. Именно таким, на его взгляд, должно быть и расстояние от Земли до Бетельгейзе. Расстояние от Земли до Бетельгейзе кажется ему в 100 раз меньше, чем мне. Мои «длины» кажутся ему сжатыми: все предметы кажутся ему в 100 раз короче, чем мне. Коэффициент укорачивания, который он фиксирует, равен ?1 – (v²/c²), и именно с таким коэффициентом я наблюдаю замедление его старения. Несомненно, это один из самых впечатляющих результатов специальной теории относительности, прекрасной в своей симметрии и железной логике.

Тот факт, что различные наблюдатели по-разному трактуют одновременность, объясняет «парадокс шеста и сарая». Вообразим, что вышеупомянутый Жак, который путешествовал со скоростью 80 % от скорости света, теперь не астронавт, а прыгун с шестом. Он бежит с девятиметровым шестом, направленным по ходу движения. Когда он будет пробегать мимо меня, мне покажется, что длина этого шеста – всего 540 см. Допустим, у нас есть девятиметровый сарай. Передняя дверь сарая открыта, задняя – закрыта. Жак вбегает в открытую переднюю дверь; когда он добежит до центра сарая, я могу закрыть дверь, и его 540-сантиметровый шест будет заперт в моем девятиметровом сарае. Затем я открываю заднюю дверь и выпускаю Жака. Но как все это выглядит для Жака? Ему должно казаться, что он – в состоянии покоя, держит девятиметровый шест. Он видит, как мой сарай налетает на него со скоростью 80 % от скорости света. По мнению Жака, длина сарая должна составлять 540 см. Находясь в центре сарая, он видит, как его девятиметровый шест высовывается из сарая и через переднюю, и через заднюю дверь. Невозможно закрыть сразу обе двери и запереть его в сарае. Ситуация кажется парадоксальной. Но ответ таков: я одновременно закрываю обе двери, спереди и сзади от шеста, одновременно – с моей точки зрения. Но для Жака два этих события не одновременны. Он иначе «нарезает» пространство-время, под углом, и ему кажется, что я закрываю двери сарая в разные моменты времени, сначала одну, потом другую. Жак не может увидеть, как две амбарные двери закрываются одновременно, но может увидеть, как его шест высовывается одновременно из первой и из второй двери сарая, пока он пробегает сарай с двумя открытыми дверьми.

Слава Эйнштейну, который смог детально проработать все эти мысленные эксперименты. Никто и никогда не пытался описывать эксперименты, исходя из постулатов, как это сделал Эйнштейн. Это была одна из наиболее оригинальных черт его работы.

Переходим к другому явному парадоксу, так называемому парадоксу близнецов. Первая близняшка, участница этого парадокса (назовем ее Гея) остается на Земле, а вторая близняшка, Астра, отправляется к звезде альфа Центавра, до которой 4 световых года. Астра летит со скоростью 80 % от скорости света, а затем возвращается также со скоростью 80 % от скорости света. Гея видит, как Астра летит со скоростью 4/5 от скорости света, поэтому ей кажется, что Астра за 5 лет долетает до альфы Центавра и за 5 лет возвращается обратно. К моменту возвращения Астры Гея повзрослеет на 10 лет. Поскольку Гея видит, как Астра летит со скоростью 80 % от скорости света, по нашей формуле ?1 – (v²/c²) Астра должна взрослеть медленно, в темпе 60 % от взросления Геи. Гея считает, что по возвращении Астра повзрослеет всего на 6 лет. Пока все понятно. Но что видит Астра? Поскольку движение относительно, почему Астра не считает, что Гея улетела от нее со скоростью 80 % от скорости света, и почему не предполагает, что по возвращении Астры на Землю Гея должна быть младше, чем на практике? Дело в том, что Астра во время пути ускорялась, а неподалеку от альфы Центавра ей пришлось притормозить, чтобы развернуться и полететь обратно. Если бы она затормозила резко, то просто размозжилась бы о стекло капитанской рубки своего корабля. В пути она меняла скорость и меняла направление. То есть она нарушала условие, заложенное в первый постулат Эйнштейна, согласно которому наблюдатель должен равномерно двигаться в одном и том же направлении с неизменной скоростью (рис. 18.3).

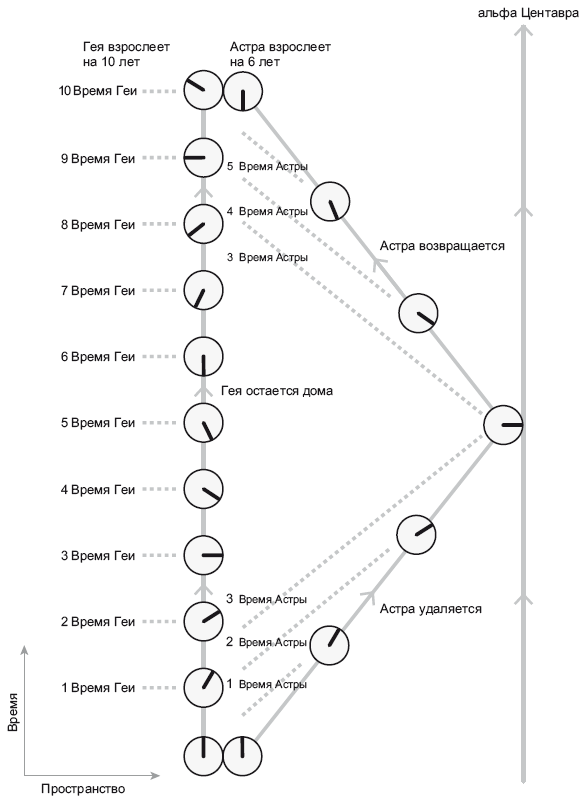
Рис. 18.3. Пространственно-временная схема парадокса двух близняшек: Геи и Астры. Гея остается дома. Ее мировая линия прямая. Астра отправляется к звезде альфа Центавра, а затем возвращается – ее мировая линия изогнута. Астра стареет медленнее, чем Гея. Часы показывают, сколько времени (в годах) истекло для каждой из близняшек. Прерывистыми линиями показаны время Геи (ET) и время Астры (AT). Иллюстрация предоставлена Дж. Ричардом Готтом

На первом этапе пути Астра летит прочь от Земли, и сегменты ее времени (AT) нарезаются, как буханка французского хлеба. В момент прибытия к альфе Центавра ее часы отсчитали 3 года звездного времени (AT), именно настолько она и повзрослела. Но линия одновременных событий «3 AT» расположена под уклоном, поэтому она пересекает Землю лишь через 1,8 года после старта. Прибывая к альфе Центавра, Астра думает, что Гея с момента старта повзрослела всего на 1,8 года. Астре кажется, что она за это время повзрослела на 3 года, а Гея – всего на 1,8 года. Ведь 1,8 года – это 60 % от 3 лет. Поэтому Астре кажется, что Гея взрослеет медленнее, поскольку себя Астра воспринимает в состоянии покоя и ей кажется, что Гея удаляется от нее со скоростью 80 % от скорости света. На этот момент Астре кажется, что Гея повзрослела меньше нее. Но подождите! Астра включает торможение и ложится на обратный курс. В этой точке мировая линия Астры изгибается. Астра изменила скорость, и в тот же момент радикально изменилось ее представление об одновременности. Когда она улетает от альфы Центавра, у нее на часах прошли все те же 3 года AT, но поскольку теперь она движется в противоположном направлении, сегмент «3 AT», охватывающий одновременные события, будет направлен в противоположную сторону и пересечет Землю через 8,2 года после старта. Отправляясь от альфы Центавра, Астра думает, что это происходит в тот самый момент, когда Гея повзрослела на 8,2 года с момента отлета Астры с Земли. За время обратного пути Астры Гея успевает прожить еще 1,8 года, а Астра за то же время – 3 года. Таким образом, между отправлением и возвращением Астры Гея успевает повзрослеть на 8,2 + 1,8 = 10 лет, а Астра за то же время – на 3 + 3 = 6 лет. Итак, и Астра, и Гея согласятся, что в момент их следующей встречи Астра должна быть моложе Геи. Гея преодолела этот отрезок по прямой мировой линии, а мировая линия Астры была изогнута. Таково решение парадокса близнецов. Идея одновременности в данном случае очень важна.

Парадокс близнецов объясняет, как попасть в будущее. Если вы хотите посетить Землю спустя тысячу лет, то вам нужно просто сесть на ракету и отправиться к звезде Бетельгейзе на 99,995 % скорости света; до Бетельгейзе 500 световых лет. Ваши часы будут идти в 100 раз медленнее, чем шли бы на Земле. По земным часам, вы должны были добраться до Бетельгейзе за 500 лет. Но за время полета вы состаритесь всего на 5 лет. Возвращайтесь обратно со скоростью 99,995 % от скорости света – и состаритесь еще на 5 лет. Но на Земле за время вашего отсутствия пройдет 1000 лет. Таким образом, вы переместитесь в будущее. Такое путешествие обошлось бы дороже, чем весь нынешний бюджет NASA (!) и, разумеется, технологий для конструирования таких космических кораблей пока не существует, но мы знаем, что подобный проект не противоречит законам физики. Протоны в ускорителях частиц разгоняются и до более высоких скоростей, поэтому известно, что достичь таких скоростей возможно. Дело за финансированием и инженерными решениями – NASA, возьмите на заметку.

Можно возразить, что высокое ускорение в точке разворота окажется убийственным. Но оказывается, что всю подобную миссию можно организовать так, чтобы перегрузки не превышали 1 g, привычного на Земле. Ноги будут твердо стоять на полу, так как ракета ускоряется. Путешествие немного затянется, зато будет комфортабельным. На пути к Бетельгейзе вы будете постепенно ускоряться в течение 6 лет и 3 недель по корабельному времени, и к этому моменту достигнете пиковой скорости в 99,99992 % от скорости света. Тогда вы будете находиться на полпути к Бетельгейзе. Затем вы станете замедляться до 1 g еще на протяжении 6 лет и 3 недель по корабельному времени, после чего останавливаетесь рядом с Бетельгейзе. Отправляетесь к Земле, постепенно ускоряясь в течение 6 лет и 3 недель, и в конце пути замедляетесь в течение 6 лет и 3 недель. За время пути вы постареете на 24 года и 3 месяца, но когда вернетесь на Землю, там пройдет 1000 лет. Чтобы путешествие получилось более комфортным, на него просто потребуется потратить больше времени (24 года, а не 10 лет). Марко Поло за 24 года совершил свое знаменитое путешествие в Китай и вернулся в Европу. Вам придется потратить на путешествие столько же времени, сколько ушло у Марко Поло на его путь, – и вы сможете побывать в будущем. В начале четвертого тысячелетия на Земле.

Российский космонавт Геннадий Падалка – величайший ныне живущий путешественник во времени. Во время работы на российской космической станции «Мир» и на Международной космической станции он провел 879 суток на околоземной орбите (космическая станция вращается вокруг Земли с высокой скоростью). Падалка состарился на 1/44 секунды меньше, чем его сверстники на Земле (в этой цифре также учтены небольшие релятивистские эффекты, связанные с пребыванием на большой высоте). Падалка вернулся на Землю и застал ее на 1/44 секунды в будущем. Да, он переместился на 1/44 секунды в будущее. Вы, наверное, посмеиваетесь. Это не такое уж далекое путешествие, но это путешествие в будущее. Однажды в ходе интервью на Национальном общественном радио меня спросили, почему так просто путешествовать в пространстве и так сложно – во времени. Я ответил, что и в пространстве мы не так уж далеко погуляли! Эйнштейн показал, что, сравнивая промежутки в пространстве и промежутки во времени, следует оперировать скоростью света. Итак, когда астроном говорит, что от нас до альфы Центавра 4 световых года, он имеет в виду, что свет от этой звезды летит до нас 4 года. Самая дальняя экспедиция, в которую отправлялись наши астронавты, – на Луну. До Луны всего 1,3 световой секунды. Люди успели слетать на 1,3 световой секунды в пространстве и заглянуть в будущее на 1/44 секунды. Это вполне сравнимые величины.

Интересно, что сегодня на свете есть два настоящих астронавта-близнеца, на примере которых можно проиллюстрировать парадокс близнецов. Марк Келли провел на низкой околоземной орбите 54 дня, а его брат-близнец Скотт Келли – 519 дней на той же околоземной орбите. Поскольку Скотт был в космосе дольше, вращаясь вокруг Земли на большой скорости, сейчас он на 1/87 секунды моложе своего брата Марка.

Я отметил, что если бы мы отправили к Меркурию астронавта, который прожил бы там 30 лет, а потом вернулся на Землю, то он оказался бы на 22 секунды моложе, чем если бы провел все это время дома. Часы на Меркурии идут медленнее, чем на Земле, поскольку Меркурий быстрее вращается вокруг Солнца (это эффект специальной теории относительности) и сильнее погружен в гравитационное поле Солнца (эффект общей теории относительности)[28].

В 1905 году Эйнштейн продемонстрировал, что путешествия в будущее возможны. Это произошло всего через 10 лет после того, как Герберт Уэллс в 1895 году изложил такую идею в своей книге «Машина времени». В рамках ньютоновской физики о подобном можно было забыть: время для всех текло одинаково, все одинаково воспринимали «настоящий момент», путешествия в будущее были невозможны. Но Эйнштейн продемонстрировал, что не все наблюдатели одинаково трактуют момент «сейчас», время оказалось гибким – часы, находящиеся в движении, тикают медленнее. Эйнштейн предоставил нам совершенно новую картину Вселенной – такую, в которой присутствуют три пространственных и одно временное измерение.

Теперь я собираюсь вывести знаменитое эйнштейновское уравнение E = mc². Допустим, у нас в лаборатории частица медленно движется со скоростью v и эта скорость намного, намного ниже скорости света c (то есть v << c). На частицу действуют законы Ньютона, и если она обладает массой m, то, согласно Ньютону, эта частица будет иметь импульс P = mv, предположим, направленный вправо. Частица испускает в противоположных направлениях два фотона, каждый из которых обладает энергией E = h?₀.Один фотон летит вправо, другой влево. Энергия фотона вычисляется по знаменитому уравнению Эйнштейна, где h – постоянная Планка, а ?₀ (греческая буква «ню») – это частота фотонов, измеренная на частице. Частица теряет энергию в количестве ?E = 2h?₀; именно такое количество энергии «с точки зрения» частицы уносят фотоны. Эйнштейн показал, что фотоны переносят не только энергию, но и импульс. Импульс фотона равен его энергии, деленной на скорость света c. C точки зрения частицы два фотона уносят в разные стороны равное количество энергии и при этом обладают одинаковым импульсом, но поскольку импульсы фотонов противоположны друг другу, с точки зрения частицы общий импульс равен нулю. Частица «считает», что находится в покое (по первому постулату Эйнштейна), и испускает два равночастотных фотона в противоположных направлениях. По правилам симметрии, если находящаяся в состоянии покоя частица испускает два равночастотных фотона в противоположных направлениях, то она остается в покое. Отдача от двух фотонов, сообщаемая частице, взаимно компенсируется. Мировая линия частицы остается прямой: скорость частицы не изменяется (рис. 18.4).

Далее рассмотрим, что происходит с двумя этими фотонами. Тот, что летит вправо, в итоге врежется в правую стену лаборатории. Он ударяется в стену, и стена при этом отскакивает вправо на крошечную величину. Эйнштейн продемонстрировал, что фотон несет импульс, равный его энергии, деленной на скорость света. Это эффект давления электромагнитного излучения: стена поглощает импульс фотона и под действием этого импульса немного подается вправо. Наблюдатель, сидящий у правой стены, увидит, что частота фотона, летящего вправо и врезающегося в правую стену, окажется выше, чем у того же фотона в момент, когда он был излучен, – ведь частица приближается к правой стене. Это пример доплеровского эффекта, который мы обсуждали в предыдущих главах. Напротив, наблюдатель, сидящий у левой стены, увидит, что к левой стене летит фотон с явным красным смещением, и, врезаясь в левую стену, этот фотон обладает меньшей частотой, чем в момент излучения, – поскольку эта частица летит прочь от наблюдателя. Более высокочастотный фотон (с синим смещением) обладает большей энергией, чем сравнительно низкочастотный фотон (с красным смещением). Соответственно правая стена от такого толчка подается вправо немного сильнее, чем левая стена – влево. Два толчка не компенсируют друг друга, и вся лаборатория получает общий результирующий импульс, направленный вправо. То есть возникает лишний импульс. Ньютон полагал, что импульс должен сохраняться (иначе было бы возможно конструировать приборы для левитации, противоречащие законам физики!), и, следовательно, лишний импульс должен откуда-то браться. Единственный возможный источник этого импульса – сама частица.

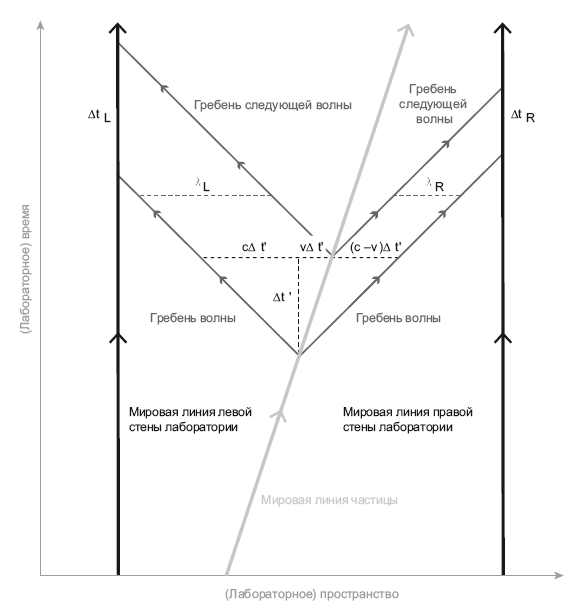
Рис. 18.4. Пространственно-временная схема мысленного эксперимента, иллюстрирующего формулу E = mc². Частица движется слева направо со скоростью v, ее мировая линия отклонена. Частица излучает фотон влево (волны которого идут вверх и влево под углом 45°) и такой же фотон вправо (волны которого идут вверх и вправо под углом 45°). Лабораторное время, проходящее между распространением двух совокупностей гребней этих волн, равно ?t’, оно показано вертикальной прерывистой линией. За это время первый гребень волны, идущей влево, успевает распространиться влево на расстояние c?t’, а частица за это время пролетает вправо на расстояние v?t’, как показано на рисунке. Длина волны (расстояние между двумя ее соседними гребнями) у движущегося влево фотона дана на рисунке:?_Л = (c + v)?t’. Волна у фотона, движущегося вправо, короче (?_П = (c – v)?t’; это связано с доплеровским смещением. Иллюстрация предоставлена Дж. Ричардом Готтом

Известно, что скорость частицы равна v << c, так что импульс частицы должен вычисляться по формуле Ньютона mv. Поскольку лаборатория приобрела импульс, у частицы он должен был уменьшиться. Но мировая линия частицы не изгибается, а остается прямой (см. пространственно-временную схему на рис. 18.4). Скорость частицы не изменяется. Если импульс частицы mvуменьшается, а скорость v остается прежней, это означает, что должна уменьшиться масса m частицы. Частица отдала какую-то энергию (в виде двух фотонов) и потеряла часть массы. Некоторая часть ее массы превратилась в энергию! Ого! Это довольно смелый вывод. Каково отношение между количеством испускаемой энергии и количеством утрачиваемой массы? Чтобы ответить на этот вопрос, нужно всего лишь вычислить доплеровские смещения двух фотонов. Общий импульс от толчка вправо, который приобретут стены лаборатории, равен 2h?₀(v/c²). Полностью эти вычисления изложены в приложении 1. Энергия, излучаемая частицей в виде двух фотонов, равна ?E = 2h?₀, так что полный импульс, приобретаемый стенами лаборатории от толчка вправо, равен ?E(v/c²). Множитель v/c² складывается из множителей v/c (доплеровское смещение) и множителя 1/c, связанного с соотношением импульса и энергии у двух фотонов. В свою очередь, общий импульс от толчка вправо, приобретаемый стенами ?E(v/c²), должен равняться тому импульсу, который утрачивает частица (?m)v. Итак, имеем тождество ?E(v/c²) = (?m)v. Разделим обе части уравнения на v (скорость частицы сокращается!). Получается ?E/c² = ?m.Теперь умножим обе части уравнения на c².Получается ?E =?mc².Избавляемся от символов ?.Остается E = mc².

В мысленном эксперименте частица утрачивает часть энергии, излучая два фотона, а также теряет часть массы. Частица, теряющая массу, излучает энергию. Излучаемая энергия относится к теряемой массе по формуле E = mc². Да, эта формула настолько простая – и настолько могучая. Член c²фигурирует в тождестве, так как и при вычислениях доплеровского смещения, и при вычислениях импульса учитывается свет, а с – скорость света.

Как известно, c – очень большая величина (приблизительно равная 300 000 км/c). Поэтому даже крошечная масса превращается в огромную энергию. По законам Ньютона кинетическая энергия грузовика равна ? mv², где m – масса грузовика, а v – его скорость. Это соотношение соблюдается, пока v << c. Грузовик, идущий со скоростью 160 км/ч, преодолевает всего 0,045 км/c (это лишь 0,00000015 c). При лобовом столкновении двух таких грузовиков, каждый из которых гонит со скоростью 160 км/ч, вся их кинетическая энергия 2(? mv²) высвободится в виде страшного взрыва. Обломки грузовиков разлетятся во все стороны. Но теперь предположим, что грузовик, состоящий из вещества, врежется в грузовик из антивещества. Два этих грузовика аннигилируют, и вся их масса превратится в энергию – это крайний случай. В таком случае произойдет взрыв, при котором выделится 2(mc²) энергии, что намного больше mv² при столкновении двух обычных грузовиков. Насколько больше? В 2/(0,00000015c)² = 89 триллионов раз. Такой взрыв при аннигиляции вещества и антивещества был бы в 89 триллионов раз сильнее, чем взрыв от столкновения двух грузовиков, врезавшихся друг в друга на скорости 160 км/ч. Именно такое колоссальное количество энергии заключено в двух крупных телах, состоящих из обычной материи.

Именно в этом заключается секрет атомной бомбы. Атомы урана или плутония распадаются, и продукты такого деления ядер весят немного меньше самих атомов. Поэтому при атомном взрыве выделяется огромное количество энергии. На Солнце при термоядерном синтезе четыре ядра водорода образуют ядро гелия, которое весит чуть меньше четырех ядер водорода; в ходе этого процесса выделяется энергия. Именно на таком топливе Солнце горит последние 4,6 миллиарда лет. Химики в точности измерили атомные массы различных элементов, и эти расчеты показывают, что масса, приходящаяся на нуклон, у разных элементов немного отличается. Следовательно, можно вычислить, сколько ядерной энергии может выделиться при термоядерном синтезе легких элементов или делении ядер тяжелых. Железо обладает наименьшей массой на нуклон. Из него невозможно добыть ядерную энергию, об этом шла речь в главе 7.

Эйнштейн, наряду с другими физиками, осознал, что его уравнение подсказывает путь к созданию атомных бомб, которые взрываются в результате деления атомного ядра. Именно об этом он рассказал 2 августа 1939 года в письме президенту Франклину Рузвельту, убеждая того в необходимости сконструировать атомную бомбу, пока этого не сделал Гитлер. Так зародился Манхэттенский проект, а физики-беженцы, работавшие в Америке и Европе, создали полноценную атомную бомбу. Как впоследствии узнали американцы, в Германии действительно была своя атомная программа, чего и опасался Эйнштейн, однако она оказалась неэффективной и не увенчалась успехом. К тому моменту, как США испытали первую атомную бомбу в Нью-Мексико, Германия уже капитулировала. Но в итоге две атомные бомбы были сброшены на Японию. Вскоре капитулировала и Япония, и на этом завершилась Вторая мировая война. Разрушительный эффект атомной бомбы оказался просто ужасающим: в результате атомных взрывов и их последствий (в том числе из-за облучения) погибли приблизительно 200 000 человек. Роберт Оппенгеймер, руководитель Манхэттенского проекта, впоследствии сказал, что первое испытание атомной бомбы напомнило ему строки из «Бхагавад-Гиты»: «Я стал смертью, разрушителем миров». Президент Трумэн принял на себя всю ответственность за решение об атомной бомбардировке. Он чувствовал, что такой шаг необходим для скорейшего завершения Второй мировой войны. Но Трумэн сказал: «Я осознаю всю трагическую важность атомной бомбы». Через много лет в личной библиотеке Трумэна была найдена книга об атомной бомбе, в которой тот подчеркнул слова из последней реплики[29] Горацио в «Гамлете»:

После войны Эйнштейн посвятил свою жизнь борьбе за ядерное разоружение.

Размышляя о путешествиях с субсветовой скоростью (которые были заведомо нереализуемы в его время), Эйнштейн тем не менее открыл принцип, изменивший ход истории. Работа Эйнштейна, проделанная им в «чудесный» 1905 год, позволила ему войти в число научных тяжеловесов, встать в один ряд с Марией Кюри и Максом Планком. Но величайшее достижение Эйнштейна еще было впереди.