Книга: Большое космическое путешествие

Глава 21 Космические струны, кротовые норы и путешествия во времени

Глава 21

Космические струны, кротовые норы и путешествия во времени

Автор: Дж. Ричард Готт

С тех пор как я исследую проблему путешествий во времени в рамках общей теории относительности, соседские дети думают, что у меня в гараже стоит машина времени. Однажды я побывал в Калифорнии на конференции по космологии и явился туда в бирюзовой спортивной куртке. Мой коллега Роберт Киршнер, в ту пору возглавлявший астрономический факультет в Гарварде, подошел и сказал: «Рич, ты, должно быть, купил эту куртку в будущем и привез сюда, ведь такого цвета еще не изобрели!» С тех пор я называю ее «куртка из будущего» и всегда прихожу в ней читать лекции о путешествиях во времени.

Обычно я вхожу на такую лекцию в этой бирюзовой куртке и несу коричневый брифкейс. Кладу брифкейс в шкафчик и поспешно выхожу. Затем возвращаюсь в футболке. Объясняю собравшимся, что у меня назначена другая встреча, и я договорился, чтобы эту лекцию прочитал вместо меня приглашенный оратор, затем выхожу снова. Снова возвращаюсь, уже в бирюзовой куртке, и говорю всем, что это «куртка из будущего». Объясняю, что не мог прочесть лекцию, потому что спешил на другую встречу, которая была назначена на то же время, что и лекция; но поскольку у меня есть машина времени, после встречи я смог просто отправиться в будущее, купить там куртку и вернуться сюда – прочесть лекцию, но уже успев немного постареть.

Тут я замечаю, что забыл принести конспект лекции о путешествиях во времени. Что же делать? Поскольку у меня есть машина времени, соображаю я, можно взять конспект уже на следующий день (после лекции) и вернуться сюда, заранее оставить где-нибудь в аудитории брифкейс с конспектом. Осматриваюсь, но нигде их не вижу. Итак, возможно, я их спрятал. Где? Да хоть в этом шкафчике. Открываю шкафчик, нахожу в нем брифкейс, открываю его – ура! Там лежит конспект лекции о путешествиях во времени.

Рассмотрим эти события, проследив их мировые линии на пространственно-временном графике. По оси абсцисс откладывается пространство, по оси ординат – время, причем будущее находится вверху. Аудитория, в которой я читаю лекцию, – это вертикальная полоса в центре. Вот как выглядит моя мировая линия (рис. 21.1).

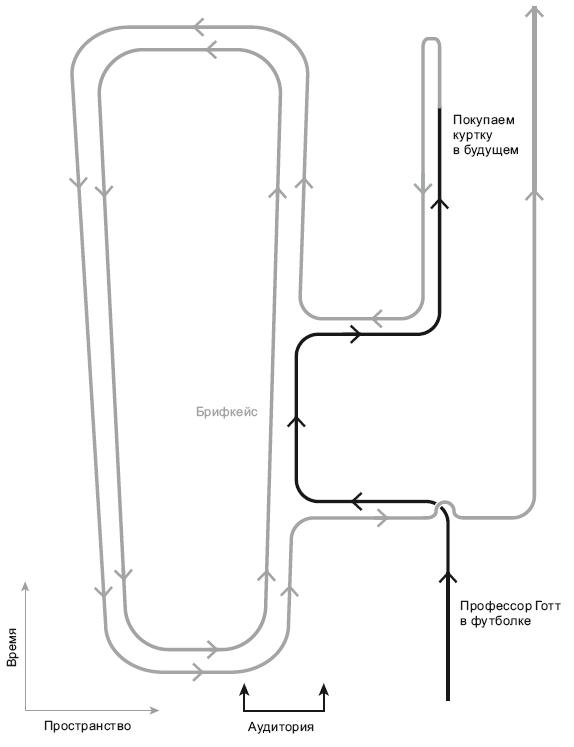
Рис. 21.1. Пространственно-временная схема хронопутешествия профессора Готта. Предоставлено Дж. Ричардом Готтом

На пространственно-временном графике я выхожу из аудитории, при этом на мне белая футболка. Ненадолго возвращаюсь в аудиторию, говорю, что не смогу прочитать лекцию, потому что спешу на встречу. Удаляюсь, успеваю на встречу, а затем лечу в будущее, где покупаю куртку. С этого момента моя мировая линия становится светло-серой. Возвращаюсь, вновь захожу в аудиторию и там читаю лекцию. Когда лекция закончена, мне нужно вернуться в прошлое незадолго до начала лекции, просто чтобы успеть занести брифкейс с конспектом этой лекции. Я войду в аудиторию, а затем быстро выйду, после чего в нее войду я же (чуть младше), в футболке. Далее я продолжу жить строго в направлении будущего. У меня получилась сложная мировая линия.

А что насчет мировой линии брифкейса? Он оказывается у меня в руках, как только я нахожу его в шкафчике. Если я буду просто держать его, то он отправится в хронопутешествие вместе со мной, и я принесу его в аудиторию еще до того, как найду в шкафчике. Мировая линия брифкейса получится кольцевой. Мировая линия брифкейса странная – у нее ни начала, ни конца. У моей мировой линии есть начало (я родился) и конец (я умер), но мировая линия брифкейса – замкнутая петля. Брифкейс в данном случае можно сравнить с частицей-джинном. Действительно, она, как и джинн, возникает из ниоткуда.

Брифкейс все время у меня на виду. Он не попадает на фабрику брифкейсов. Физики, исследующие путешествия в прошлое, вынуждены учитывать частицы-джинны, когда рассуждают о квантовых эффектах. Что, если на моем брифкейсе появится небольшая потертость, когда я заберу его с собой с лекции? Игорь Новиков считает, что такой износ, который претерпевает джинн-частица, должен в какой-то момент «исправляться», чтобы она вернулась в исходное состояние, – и мой брифкейс не исключение. При этом не нарушаются законы энтропии, так как брифкейс – это не изолированная система; энергия, необходимая на его починку, поступает извне.

Информация также может выступать в качестве джинна. Допустим, я прилетаю в 1915 год и даю Эйнштейну верные уравнения поля для общей теории относительности. Он может их записать и опубликовать. Откуда взялась эта информация? Я усвоил ее из статьи Эйнштейна, а Эйнштейн узнал ее от меня. Получается кольцевая мировая линия.

Законы физики допускают существование джинн-частиц – просто их возникновение маловероятно, – причем чем массивнее и сложнее такие частицы, тем менее вероятно их возникновение. Аналогичная история могла бы произойти, если бы я нашел на полу в поточной аудитории клочок бумаги и взял с собой не брифкейс, а этот клочок. В таком случае бумажка стала бы джинном, а носить ее с собой проще, чем брифкейс. Еще проще – я мог бы банально взять электрон и унести его с собой, а затем вернуть в прошлое, в лекционную аудиторию. Просто не столь вероятно найти для этой цели такой массивный объект, как брифкейс, да еще с конспектами к лекции о путешествиях во времени. Думаю, возможны и такие сложные джинны, но возникать они будут исключительно редко.

Путешествие в прошлое происходит при наличии мировой линии, которая закольцовывается в прошлое. Обычная ситуация отражена на рис. 18.1: мировые линии Земли и других планет идут по спирали вдоль мировой линии Солнца. Ничто не может двигаться со сверхсветовой скоростью, и все мировые линии устремлены в будущее. На рис. 21.2 показана ситуация, когда мы путешествуем в прошлое. Мировая линия путешественника замыкается сама на себя, и он становится свидетелем каких-то событий из собственного прошлого. Путешественник начинает путь внизу (в прошлом) и поднимается вверх до тех пор, пока не встречает повзрослевшего себя, который ему говорит: «Привет! Я – это ты в будущем! Прилетел в прошлое поздороваться с тобой». Он отвечает: «Правда?» и отправляется по петле обратно в прошлое. Затем он встречает себя же в юности и говорит: «Привет! Я – это ты в будущем! Прилетел в прошлое поздороваться с тобой». Молодой «двойник» отвечает: «Правда?» Путешественник во времени участвует в этой встрече дважды: как молодой и как более взрослый человек, но сама ситуация складывается лишь однократно. Можно сравнить ее с четырехмерной скульптурой, на которую нанесены мировые линии. Она никогда не меняется: именно так и выглядит вся картина. Если вам интересно, как ощущалась бы подобная ситуация, – просто проведите пальцем по мировой линии и посмотрите, какие еще мировые линии с ней пересекутся.

Здесь открывается один из варантов решения знаменитого парадокса бабушки: что бы случилось, если бы я отправился в прошлое и случайно убил собственную бабушку еще до того, как она родит мою мать? В таком случае она не родит мою мать, а мать – меня, и тогда меня не будет, я не смогу отправиться в будущее и убить мою будущую бабушку. Это, в свою очередь, означает, что она без проблем родит мою мать, а мать – меня. Парадокс. Традиционное решение парадокса бабушки таково: путешественники во времени не могут изменить прошлое. Они всегда – часть прошлого. Да, вы могли отправиться в прошлое и выпить в компании бабушки чаю с печеньем, когда она была еще юной девушкой, но не могли убить ее, поскольку она должна родить вашу мать, которая родит вас. Решение должно быть самосогласованным. Кип Торн, Игорь Новиков и их коллеги сформулировали ряд мысленных экспериментов из области путешествий во времени, сталкивая бильярдные шары; они пытались показать, что всегда можно найти самосогласованные решения, не содержащие парадоксов.

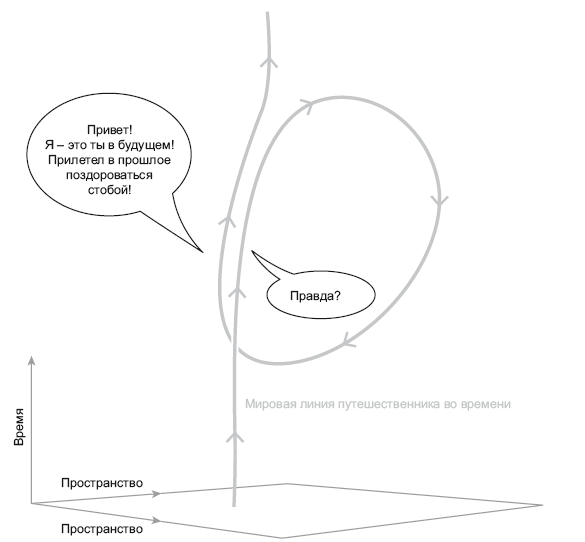
Рис. 21.2. Пространственно-временная схема мировой линии путешественника в прошлое. Иллюстрация адаптирована из J. Richard Gott, Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

Не беспокойтесь по поводу изменения истории: как бы вы ни старались, ничего у вас не выйдет. Если вернуться на «Титаник» и предупредить капитана об айсберге, то капитан проигнорирует ваши слова, точно как он не придал значения всем остальным сообщениям об айсбергах, – ведь мы знаем, что корабль затонет. Вы убедитесь, что изменить ход событий невозможно. Хронопутешествия в фильме «Невероятные приключения Билла и Теда» построены по тому же принципу самосогласованности.

Альтернативный вариант решения парадокса бабушки – это эвереттовская многомировая теорияквантовой механики. Мнения физиков по поводу этой теории разнятся, но давайте для начала разберемся, как она устроена. В многомировой теории считается, что множество параллельных миров могут сосуществовать, как железнодорожные пути в маневровом парке. Мы видим одну историю, словно наш поезд идет по конкретному пути. События, которые мы наблюдаем, подобны станциям, сменяющим друг друга. Вот Вторая мировая война… вот люди высаживаются на Луне и так далее. Но существует множество параллельных миров. Есть мир, где Вторая мировая война не произошла. Такая теория основана на подходе к квантовой механике как к сумме множества историй, предложенном Ричардом Фейнманом. Фейнман понял, что для расчета вероятности любого исхода того или иного будущего эксперимента нужно учесть все возможные истории, которые могли бы к нему привести. Кому-то кажется, что это просто очередное странное правило расчетов в квантовой механике, но сторонники многомировой модели считают, что все эти истории реальны и взаимодействуют друг с другом. Дэвид Дойч считает, что путешественник во времени может отправиться в прошлое и убить там свою бабушку, когда она была еще юной девушкой. В таком случае возникнет новое ответвление истории: в этом варианте истории будут и живой хронопутешественник, и его мертвая бабушка. Тот путь, где хронопутешественник все-таки родился и его бабушка осталась жива, также продолжает существовать. Путешественник по-прежнему помнит часть своей биографии, свершившейся до поворота на новый путь. Оба пути существуют.

Теперь у нас есть два адекватных решения парадокса бабушки. Первое – консервативное, где пространство-время представлено в виде единой самосогласованной четырехмерной скульптуры, неизменной по сути. Второе – более радикальная многомировая интерпретация квантовой механики. Оба решения работают.

Далее, если вернуться к мировой линии путешественника во времени, которая закольцовывается сама на себя в прошлом, то можно заметить в ней один изъян. Свет на этой схеме летит под углом 45°. Когда хронопутешественник переваливает через вершину, чтобы начать возвращение в прошлое, в какой-то точке уклон его мировой линии относительно оси времени должен быть больше 45°. Это означает, что в какой-то момент он должен превысить скорость света. На самом деле, переваливая через вершину схемы, он движется с бесконечной скоростью. Феномен взаимосвязи полетов со сверхсветовыми скоростями и путешествий во времени схвачен в следующем лимерике А.Г. Р. Баллера:

Проблема в том, что (как продемонстрировал Эйнштейн в своей специальной теории относительности) невозможно сконструировать ракету, которая развивала бы сверхсветовую скорость. Если ваша скорость не превышает скорости, света, то ваша мировая линия никогда не расположится под углом более 45° относительно оси времени, и вернуться в прошлое не получится. Однако в общей теории относительности Эйнштейна, где пространство-время считается искривленным, можно обогнать луч света, срезав путь, если двинуться либо через кротовую нору, либо (что будет рассмотрено ниже) по космической струне. Если обогнать луч света, то, подобно нашей шустрой мисс, можно улететь в прошлое.

Допустим, у нас есть лист бумаги, на котором одно пространственное измерение откладывается по горизонтали, а время – по вертикали (рис. 21.3). В таком случае ваша мировая линия – это зеленая полоска на данном рисунке. Вы ленивы и просто сидите дома, поэтому ваша мировая линия идет ровно от нижнего до верхнего края листа. Однако в искривленном пространстве-времени действуют иные правила. Давайте свернем лист в цилиндр по горизонтали, склеив сверху лист скотчем. Теперь ваша мировая линия – это круг, уходящий в прошлое.

Вы все время движетесь вперед в будущее, но на самом деле заворачиваете в прошлое. То же самое произошло с экспедицией Магеллана: моряки все время плыли на запад, обогнули всю Землю и вернулись обратно в Европу. Этого бы ни в коем случае не произошло, если бы поверхность Земли была плоской. Аналогично, хронопутешественник все время движется в будущее, но, если пространство достаточно искривлено, он может вернуться к событиям, свершившимся у него в прошлом.

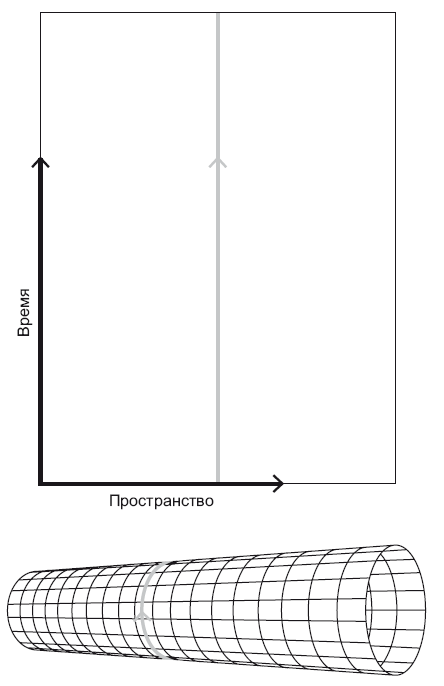
Рис. 21.3. В искривленном пространстве-времени мировая линия может свернуться в кольцо и уйти в прошлое. Иллюстрация адаптирована из J. Richard Gott, Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

Такие ситуации допускаются в различных решениях общей теории относительности. Прежде чем перейти к их обсуждению, позвольте рассказать о космических струнах. В 1985 году я нашел точное решение эйнштейновских уравнений поля для геометрии, обернутой вокруг космической струны. Александр Виленкин из университета Тафтса нашел приблизительное решение, а я – точное. Уильям Хискок из университета штата Монтана независимо нашел точно такое же точное решение, так что мы с ним разделили честь этого открытия. Решение позволяет судить, какова геометрия пространства вокруг космической струны.

Но что такое космическая струна? Это тонкая (тоньше атомного ядра) натянутая нить концентрированной квантовой энергии вакуума; такая нить могла сохраниться со времен Большого взрыва. Многие теории из физики частиц прогнозируют существование таких струн. Мы еще не нашли подобных струн, но упорно ищем.

Физики узнали, что вакуум (пустое пространство, где нет ни частиц, ни фотонов) может пропитываться энергией поля, пронизывающего пространство. Такая концепция, например, применима к недавно открытому полю Хиггса и к связанной с ним частице – бозону Хиггса. После того как бозон Хиггса удалось обнаружить на Большом адронном коллайдере, Франсуа Энглер и Питер Хиггс в 2013 году получили Нобелевскую премию по физике за свои теоретические исследования, предвосхитившие эту находку. В главе 23 мы поговорим о том, что, как считается сегодня, в новорожденной Вселенной энергия вакуума была очень велика. После того как из этой энергии вакуума родились обычные частицы, оставшаяся энергия вакуума могла остаться заключена в тонких нитях – космических струнах, отличающихся высокой концентрацией энергии. Представьте себе, как будто целое поле было покрыто снегом, снег растаял, и на поле кое-где остались стоять снеговики. Аналогично, космические струны состоят из энергии вакуума, сохранившейся со времен зарождения Вселенной.

У космических струн нет кончиков; либо они бесконечны, если сама Вселенная не имеет краев, либо они свернуты в замкнутые петли. Представьте себе (бесконечно длинные) макаронины и макаронные колечки. Считается, что в природе могут существовать как бесконечно длинные струны, так и струнные петли. Большая часть массы в сети космических струн приходится на бесконечно длинные струны.

Рассуждая о геометрии пространства вокруг космической струны, следует задать вопрос: как должно выглядеть поперечное сечение через плоскость, перпендикулярную струне? Можно предположить, что оно будет похоже на лист бумаги с точкой посередине – там, где струна проходит через плоскость. Но считается, что космическая струна должна быть очень массивной – примерно миллион миллиардов тонн (10¹⁵) на сантиметр; следовательно, она существенно искривляет пространство вокруг себя. Вся структура напоминает не лист бумаги с точкой посреди него, а пиццу, в которой вырезан один ломтик (рис. 21.4).

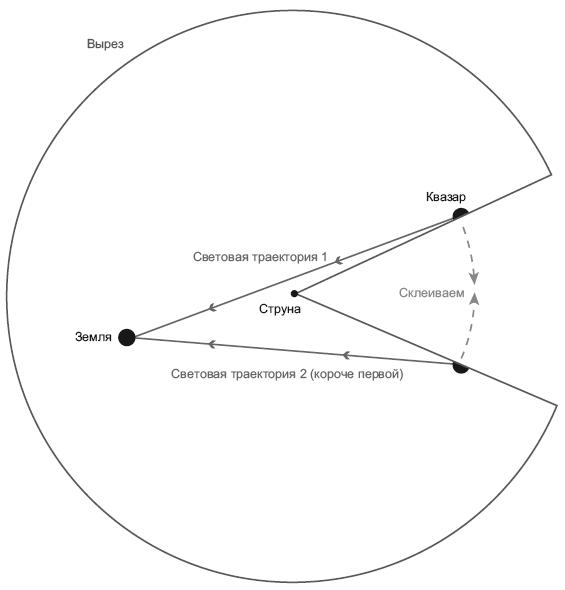
Рис. 21.4. Геометрия вокруг космической струны. Иллюстрация адаптирована из J. Richard Gott, Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

Берем пиццу и просто убираем из нее один ломтик. Съедаем его. Съели. Все, его нет. Берем остаток пиццы и аккуратно притягиваем друг к другу краешки выреза, так, чтобы они закрыли то пространство, где находился съеденный кусок. Стягиваем их так, чтобы пицца приобрела форму конуса. Именно такова геометрия у поперечного сечения пространства вокруг струны. Пространство напоминает конус. Сама струна проходит через центр пиццы. Коническая геометрия демонстрирует, что длина окружности не равна 2? радиуса пиццы. Все потому, что в пицце не хватает ломтика, – окружность оказалась бы больше, не будь пицца щербатой. Как видите, она не подчиняется законам евклидовой планиметрии.

Угловая ширина недостающего ломтика пропорциональна массе на единицу длины струны, и для космических струн, которые в самом деле могли образовываться в ранней Вселенной (согласно теориям великого объединения в физике частиц, струны могли возникать в эпоху, когда начало распадаться единство слабого, сильного и электромагнитного взаимодействий), этот угол был довольно мал – может быть, полсекунды дуги или даже меньше. Это очень малая, но тем не менее обнаружимая величина.

На рис. 21.4 струна изображена в центре, и заметно, где был сделан вырез, то есть где склеены два его края. Допустим, я нахожусь на Земле и рассматриваю квазар, расположенный за струной. Свет может долететь до меня по любой из двух этих прямолинейных траекторий (траектория 1 и траектория 2), проходящих по обе стороны от струны. Если склеить края пиццы на месте разреза так, чтобы лист бумаги сложился в конус, то две траектории световых лучей обогнут струну с разных сторон. Световые траектории искривятся под действием гравитационного линзирования. Именно такой эффект возникает, когда луч света пролетает мимо Солнца, мы обсуждали его в главе 19. Но траектории лучей света максимально прямолинейны. Я провел их по линейке. Если склеить «бумажную пиццу» наподобие конуса, то можно было бы провезти игрушечный грузовичок либо по траектории 1, либо по траектории 2 от квазара до Земли, никуда не сворачивая. Обе траектории являются геодезическими. Поскольку два луча света могут лететь по прямолинейным траекториям от квазара до Земли, мы видим две копии квазара по противоположные стороны от космической струны. Можно искать космические струны, высматривая в небе пары квазаров, так, чтобы два квазара располагались один напротив другого, словно пуговицы на мундире. Мы пока не нашли квазаров, линзированных под действием космической струны, но продолжаем искать.

Одно из замечательных свойств этой картины заключается в том, что длина двух световых траекторий может отличаться. Так, на рис. 21.4 траектория 2 немного короче траектории 1. То есть если я полечу на ракете от квазара к Земле на скорости 99,9999999999 % от скорости света, то смогу обогнать луч света, летящий по траектории 1, так как ему придется преодолеть большее расстояние. Я срежу путь и приду первым!

Хотя мы еще не видели космических струн, нам уже доводилось наблюдать подобное гравитационное линзирование в случае с галактикой, расположенной между нами и квазаром. Мы видим одинаковые копии далекого квазара QSO 0957+561 по обе стороны от линзирующей его галактики. Из-за искривления пространства-времени под действием этой галактики свет изгибается точно таким же образом, как и в случае космической струны. В таком случае яркость далекого квазара варьируется. Группе астрономов под руководством Эда Тёрнера, в состав которой также входили Томислав Кундич, Уэс Колли и я, удалось измерить в обеих «копиях» квазара один и тот же выброс, который был зафиксирован в одной копии с запаздыванием на 417 дней по сравнению с другой. Это малая толика того периода, за который свет этого квазара долетает до нас, – 8,9 миллиарда лет! Но если вам интересно, можно ли путешествовать быстрее света, то в данном случае ответ утвердительный: можно! Один луч света приходит на 417 дней раньше другого. Оба луча летели в вакууме с одинаковой скоростью, просто один из них срезал путь.

Итак, изучение квазаров-«близнецов» – один из способов поиска космических струн. До сих пор все известные случаи такого рода объясняются галактическим линзированием, но мы и ожидаем, что квазары, линзированные космическими струнами, должны встречаться реже, так что здесь нет ничего удивительного. Поиски продолжаются.

Космические струны натянуты и обычно вибрируют со скоростями примерно вдвое меньше скорости света. Точно как два луча света изгибаются навстречу друг другу, проходя по разные стороны от космической струны, так и два космических корабля, находящихся в состоянии покоя, можно подтянуть друг к другу, когда между ними стремительно движется космическая струна. Когда струна проходит между ними, они, набирая скорость, несутся друг к другу. Теперь допустим, что один из этих кораблей – Земля, а другой – реликтовое излучение (РИ). Двигающаяся струна дает небольшое доплеровское смещение в спектре расположенного за ней РИ. Если струна движется между РИ и нами слева направо, то РИ кажется чуть теплее слева от струны, чем справа. Мы ищем подобные эффекты. Колеблющиеся замкнутые струны, похожие на вибрирующие резиновые жгуты, могут давать гравитационные волны, и в будущем мы их также планируем искать при помощи аппаратов типа LIGO. Следовательно, есть ряд перспективных способов поиска космических струн.

Как можно было бы воспользоваться таким эффектом «срезания пути», который обеспечивает космическая струна? В 1991 году я нашел точное решение уравнений поля Эйнштейна в рамках общей теории относительности для двух движущихся космических струн. В этом решении две параллельные космические струны движутся одна мимо другой, как мачты двух шхун, плывущих ночью встречными курсами. Вертикальная струна 1 движется слева направо, а вертикальная струна 2 движется справа налево. Как должна выглядеть геометрия пространства вокруг двух этих струн?

Неудивительно, что на этот раз в пицце не хватает двух ломтиков. Поперечное сечение, перпендикулярное двум космическим струнам, напоминает лист бумаги с двумя вырезами, и из него можно сложить бумажный кораблик (рис. 21.5). Когда бумага разложена на столе, мы видим, где недостает двух кусков. Один начинается на струне 1 и продолжается вверх по странице, а второй начинается на струне 2 и продолжается вниз по странице. (Две струны вытянуты по направлению к вам, перпендикулярно странице.) Теперь можно срезать путь двумя способами. Если стартовать с планеты A на этом рисунке, то можно попасть на планету B по прямолинейной траектории, пролегающей между космическими струнами, она обозначена «Путь 2». Но есть и более короткий путь, который позволит вам добраться на планету B быстрее, это путь вокруг космической струны 1. Аналогично, другой сокращенный путь – путь 3 – позволяет вернуться с планеты B на планету A быстрее, чем по пути 2. Если стартовать с планеты A и отправиться на планету B на скорости 99,9999999 % от скорости света, то можно обогнать тот луч света, что летит непосредственно к планете B по пути 2. Путь 1 короче пути 2, поскольку не хватает одного «ломтика пиццы». Таким образом, можно отчалить от планеты A уже после того, как с нее по пути 2 улетит луч света, и прибыть на планету B раньше этого луча. Отправление с планеты A и прибытие на планету B – это два события, которые пространственноподобно разделены по пути 2; между ними в пространстве насчитывается больше световых лет, чем во времени – календарных лет. Вы обгоняете луч света и поэтому фактически движетесь со сверхсветовой скоростью, поскольку срезаете путь. Таким образом, некоторый наблюдатель, стремительно летящий влево, – назовем его Космо – сочтет два этих события одновременными. Поскольку его скорость меньше скорости света, он шинкует пространство-время под наклоном, как будто режет французский хлеб, и считает, что вы стартуете с планеты A и прибываете на планету B одновременно.

Теперь предположим, что в верхней части решения у нас будет стремительное движение вправо, которое захватывает и космическую струну 1, и Космо заодно с ней. Теперь струна 1 не стационарна, а быстро движется, и поскольку движение относительно, Космо больше не летит влево, а неподвижно застыл в центре. Космо смотрит на свои часы и видит, как вы в 12:00 улетаете с планеты A и в 12:00 прибываете на планету B. Если такой трюк вышел у нас однажды – выйдет и повторно.

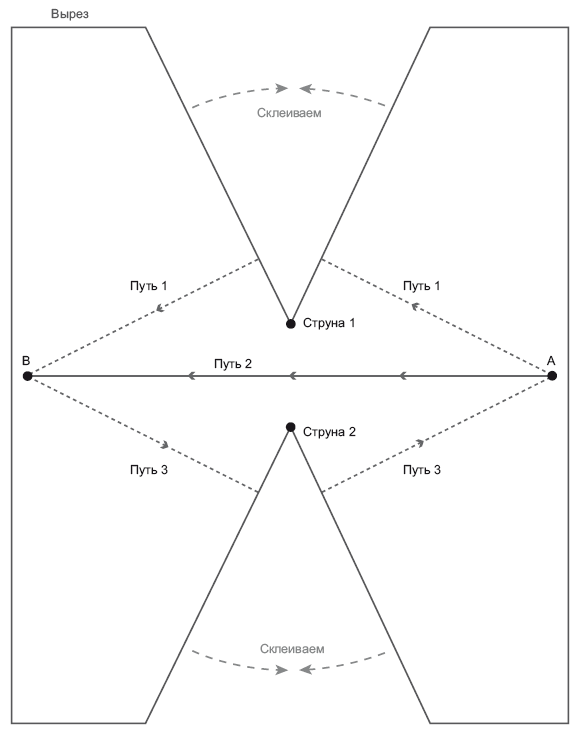
Рис. 21.5. Геометрия пространства вокруг двух космических струн. Иллюстрация адаптирована из J. Richard Gott, Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

Быстро промотайте нижнюю часть решения влево, чтобы ровно с такой высокой (субсветовой) скоростью у нас двигалась струна 2. Можно улететь с планеты B и срезать путь по траектории 3, обогнав таким образом луч света, летящий к планете A по пути 2. Между вашим отбытием с планеты A и прибытием на планету B будет больше световых лет в пространстве, чем календарных лет во времени. Если нижняя часть решения движется достаточно быстро (но все-таки медленнее света), то, с точки зрения Космо, струна 2 движется практически со скоростью света и, с точки зрения Космо, вы одновременно улетите с планеты B и прибудете на планету A. Итак, если (по его часам) вы улетите с планеты B в 12:00, то и ваше возвращение на планету A он зафиксирует в 12:00. Но вы улетели с планеты A в 12:00 по времени Космо. Вы улетаете с планеты A и возвращаетесь на нее, оставаясь в одном и том же месте в одно и то же время. Вы можете вернуться во времени и пожать руку себе же, более молодому! Вы слетали к одному из событий в вашем прошлом. Да, это настоящее путешествие в прошлое.

Вот как эта ситуация выглядит для вас. Вы прибываете в космопорт на планете A. Там вас встречает ваш двойник, старше вас, и говорит: «Привет! А я уже однажды летал вокруг струн!» Вы отвечаете: «Серьезно?». Затем вы на вашем корабле отправляетесь вокруг струны 1 и прибываете на планету B по пути 1. После этого вы сразу же улетаете с планеты B, летите вокруг струны 2 и прибываете обратно на планету A в то самое время, когда вам предстоит встретить себя же, более молодого. Говорите: «Привет! А я уже однажды летал вокруг струн!» И он вам отвечает: «Серьезно?»

Нарушает ли каким-то образом такая встреча с молодым «собой» закон сохранения энергии? Все-таки сначала вы существовали в одном экземпляре, а при этой встрече вас очевидно двое. Нет, поскольку общая теория относительности требует лишь локального сохранения энергии. Таким образом, масса-энергия в комнате может возрасти, лишь если в эту комнату извне поступит новая масса-энергия. Но вы, путешествуя во времени, входите в комнату как кто угодно другой. Масса-энергия возрастает, поскольку вы входите. Итак, локальное сохранение энергии в этих решениях соблюдается.

Важно, что две струны, проходя одна мимо другой, движутся в противоположных направлениях. В таком случае вам просто нужен космический корабль, который сможет полететь вокруг двух этих струн, – и вы сможете вернуться туда, откуда отправились. Майкл Лемоник написал для журнала Timeстатью о моей машине времени; в ней он поместил картинку, на которой я держу две струны и модельку космического корабля.

Курт Катлер из Калтеха открыл очень интересное свойство моего решения для двух струн. Была эпоха, до наступления которой никаких путешествий в прошлое не происходило. Когда в далеком прошлом две струны находились очень далеко друг от друга, на их облет уходило очень много времени, и после старта вы всегда возвращались домой на планету A. Но когда струны достаточно сближаются, просто проходят одна мимо другой, вы можете облететь эти струны и вернуться в собственное прошлое. Такое событие происходит в области хронопутешествия. На рис. 21.6 смоделирована его трехмерная пространственно-временная схема.

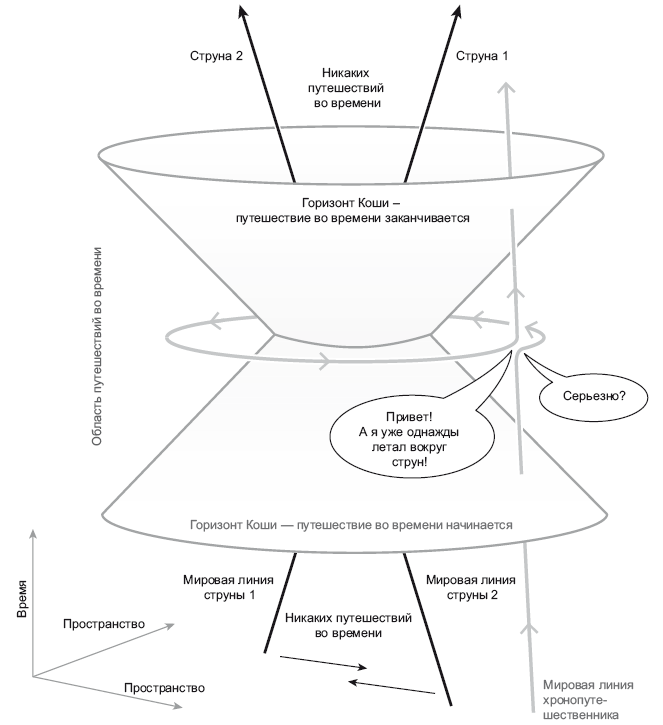
Рис. 21.6. Пространственно-временная схема машины времени, использующей свойства двух космических струн. Иллюстрация адаптирована из J. Richard Gott, Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

Время показано по вертикали, а два пространственных измерения изображены по горизонтали, в перспективе. Поскольку струна 1 движется вправо, ее мировая линия – это прямая, отклоненная вправо. Струна 2 движется влево, и ее мировая линия – прямая, отклоненная влево. Также показана мировая линия хронопутешественника. Он движется медленно, поэтому его прямая линия почти вертикальна – до тех самых пор, пока он не прибудет на планету A. Затем вы видите, как он улетает в полдень, огибает две струны и прибывает обратно в полдень. Приветствует себя же, более молодого. Затем проживает остаток жизни, и его мировая линия вновь почти вертикальна. Катлер обнаружил, что область путешествий во времени ограничена поверхностью, именуемой горизонт Коши; она выглядит как два абажура, один из которых поставлен на другой вверх ногами. Обратите внимание: хронопутешественник, приближающийся к планете A, начал путь в далеком прошлом, там, где путешествия во времени были невозможны. Затем он пересекает горизонт Коши, где начинается путешествие во времени. После этого он может видеть других хронопутешественников, прибывающих из будущего. На протяжении какого-то времени хронопутешествия возможны, но затем он пересекает второй горизонт Коши, после которого такая возможность исчезает. После этого он уже не в состоянии встретить хронопутешественников из будущего. К этому моменту две космические струны будут настолько удалены друг от друга, что хронопутешественник не сможет более их огибать и возвращаться к тому моменту, с которого начал путь.

Вот и ответ на знаменитый вопрос Стивена Хокинга: «Где же все путешественники во времени?» Если путешествия во времени возможны, то почему при знаменитых исторических событиях не толпятся «туристы-хронолетчики» из будущего? Почему мы не наблюдаем на пленке, где запечатлено убийство Кеннеди, пришельцев из далекого будущего с видеокамерами, в серебристых скафандрах? Дело в том, что, создавая машину времени, которая способна переносить пилота в будущее, искривляя пространство-время, мы создаем горизонт Коши, и только преодолев этот горизонт, можно увидеть пришельцев из будущего. Но эти путешественники не могут вернуться назад в те времена, когда машины времени еще не существовало. Если сконструировать машину времени в 3000 году, то ею можно будет пользоваться и, в принципе, на ней можно будет слетать из 3002-го в 3001 год, но забраться в прошлое до 3000 года она не позволит, поскольку именно в 3000 году была сконструирована первая машина времени. Мы до сих пор не видели таких хронопутешественников, поскольку пока еще не создали таких машин времени! Это справедливо и для машин времени, при работе которых используются кротовые норы, а также для варп-двигателей, о которых мы вскоре поговорим. Но это означает, что даже если мы прочешем прошлое и не найдем там пришельцев из будущего, мы все равно можем когда-нибудь пересечь горизонт Коши и обнаружить, что вокруг вдруг начинают появляться такие хронопутешественники.

Предполагается, что космические струны могут быть как бесконечными (о которых мы сейчас рассуждаем), так и замкнутыми в петли. Причем, поскольку космические струны натянуты, следует ожидать, что они должны колебаться со скоростями примерно в половину скорости света. Но на практике нам вряд ли повезет найти две бесконечные космические струны, проходящие одна мимо другой как раз с такой скоростью, при которой они сгодятся для создания машины времени. Космические струны, предусматриваемые теориями великого объединения, должны двигаться со скоростями не менее 99,99999999996 % от скорости света (это субсветовая, очень высокая скорость) – только в таком случае из них может получиться машина времени. Однако всегда можно найти струну, замкнутую в петлю, и гравитационно управлять ею (при помощи массивных космических кораблей) так, чтобы она сильно сжималась под действием собственного натяжения. Струнная петля напоминает резиновый жгут. Прогоняя мимо нее массивные космические корабли, можно оперировать ею так, чтобы два очень длинных и прямолинейных отрезка этой струны, колеблясь, проходили один мимо другого с достаточной скоростью, нужной для создания машины времени. Мне удалось продемонстрировать (в статье о машине времени на базе космических струн, опубликованной в журнале Physical Review Letters в 1991 году), что струнная петля в таком случае оказывается как раз на грани схлопывания в черную дыру, которая будет образовываться вокруг нее. Это нехорошо!

Я показал, что область, допускающая путешествия во времени, вполне может быть заключена внутри черной дыры. Впоследствии мы с Ли Синь Ли обнаружили, что дополнительная масса ракеты, огибающей струны в машине времени, также может спровоцировать образование черной дыры вокруг вас.

У струнной петли должно быть два длинных прямолинейных сегмента, проходящих один мимо другого на высокой скорости в противоположных направлениях. Следовательно, петля будет обладать некоторым моментом импульса и, следовательно, при этом будет образовываться именно вращающаяся черная дыра.

Итак, давайте поговорим о вращающихся черных дырах. Как упоминалось в главе 20, точное решение эйнштейновских уравнений поля для вращающейся черной дыры (обладающей моментом импульса) открыл в 1963 году Рой Керр. О том, что происходит в недрах вращающейся черной дыры, соответствующей такому решению (в пределах горизонта событий), удалось узнать благодаря работе Брэндона Картера. Керровское решение предусматривает два критических радиуса: r₊, соответствующий горизонту событий, и меньший радиус r_-, соответствующий внутреннему горизонту Коши.

В центре керровской черной дыры находится не точечная, а кольцевая сингулярность. Бесконечная кривизна достигается лишь на этом кольце (на самом деле, это почти бесконечная кривизна, она будет немного «размазываться» под действием квантовых эффектов). Если вы врежетесь в это кольцо, то вас убьют приливные силы (описанный в главе 20 эффект, одновременно напоминающий пытку на дыбе и в «железной деве»). Но интересно, что аспирант, упавший во вращающуюся черную дыру, сможет миновать кольцевую сингулярность. Она не блокирует пути в будущее. Аспирант пересекает сперва r₊(горизонт событий), а затем r_- (горизонт Коши). Кольцевая сингулярность находится внутри горизонта Коши, и аспирант может ее увидеть как раз в тот момент, когда будет пересекать горизонт Коши. Если аспирант проскочит через это кольцо как через обруч, то он войдет в совершенно новую большую новую вселенную (Вселенная 1). Картер показал, что если аспирант попадет через кольцо во Вселенную 1 и особым образом обогнет окружность, будучи по ту сторону, то сможет запрыгнуть через это кольцо обратно на нашу сторону к моменту, который предшествовал входу в кольцо. Аспирант сможет совершить небольшой вояж в прошлое и поздороваться со своим чуть более юным «я» – таким, каким он был до первого проникновения через кольцо. Разумеется, никто, находящийся за пределами черной дыры, не увидит ничего из происходящего в черной дыре, поскольку все эти вещи совершаются за горизонтом событий. Когда аспирант входит в пределы горизонта Коши, он попадает в область, где возможны путешествия в прошлое (см. рис. 21.6). Горизонт Коши отмечает начало эпохи, в которой возможны путешествия во времени, и эта эпоха целиком заключена в пределах горизонта событий черной дыры. Аспирант никогда не сможет вернуться в нашу Вселенную и похвастаться перед друзьями своими путешествиями во времени. Далее он сможет отправиться в будущее. На пространственно-временном графике таких событий кольцевая сингулярность, с одной стороны, не мешает аспиранту попасть в будущее. Он покидает область, допускающую путешествия во времени, пересекая второй горизонт Коши (опять же, см. рис. 21.6), после которого может вынырнуть еще в одной большой Вселенной, такой как наша (Вселенная 2). Он выходит из так называемой вращающейся белой дыры во Вселенную 2. Он может там и прожить всю оставшуюся жизнь либо вернуться в черную дыру и отправиться странствовать в новые вселенные, всякий раз оказываясь в будущем. Все это напоминает путь по многоэтажному зданию. Представьте себе, что заходите в лифт на первом этаже – это наша Вселенная. Двери закрываются, и вы отправляетесь вверх – во Вселенную с первого этажа вы больше никогда не вернетесь. Она осталась у вас в прошлом. Двери вновь распахиваются, и вы видите новую вселенную (Вселенная 1). Можете в ней остаться и прожить здесь всю жизнь либо запрыгнуть обратно в лифт и вновь пройти через кольцо. В таком случае вы вновь подниметесь вверх, и двери лифта откроются в следующей Вселенной (Вселенная 2). Можете здесь выйти и прожить всю оставшуюся жизнь либо остаться в лифте и продолжить путь в будущее, вечно глядя, как двери лифта открываются и закрываются на входе в новые Вселенные. Но вам никогда не вернуться на первый этаж, в нашу Вселенную. Керровское решение показывает, что все это действительно происходит во вращающейся черной дыре, которая действительно сформировалась в нашей Вселенной в какой-то момент в прошлом.

Но здесь нужно учесть и некоторые подводные камни.

В главе 20 мы говорили о том, что профессор остается за пределами черной дыры, на безопасном расстоянии от нее. Фотоны, отправленные профессором и падающие в черную дыру, могут быть приняты аспирантом даже после того, как аспирант пересечет горизонт событий. Профессор сможет отправлять аспиранту сообщения вроде «классно сработано» или «продолжай в том же духе – у тебя получится отличная диссертация». Аспирант получит все эти весточки. Между пересечением горизонта событий и горизонта Коши – для аспиранта это два отдельных события, между которыми проходит конечное время, порядка нескольких часов в случае черной дыры, чья масса в несколько миллиардов раз превышает солнечную, – аспирант сможет наблюдать всю бесконечную грядущую историю нашей Вселенной, разворачивающуюся за пределами черной дыры. Новостные заголовки будут долетать до аспиранта все быстрее и быстрее. До пересечения горизонта Коши аспирант, в принципе, получит бесконечное количество новостных сообщений за конечное время – именно так все должно быть в соответствии с керровским решением.

Историкам это понравится. Если аспирант интересовался будущим нашей Вселенной, то он сможет увидеть всю эту бесконечную историю за конечное время. Но это опасно! Такие ускоренные новости будут прилетать в бешеном темпе как поток фотонов с сильным голубым смещением. Фотоны приобретают голубое смещение, поскольку падают в черную дыру и получают при этом энергию. Все фотоны получают голубое смещение с таким же коэффициентом, с каким ускоряется поток новостей. Высокоэнергетические фотоны такого рода относятся к спектральному диапазону гамма-лучей, и они могут погубить аспиранта. Фотоны приобретут случайно распределенные (стремящиеся к бесконечности) величины синего смещения по мере приближения аспиранта к горизонту Коши, а затем образуют искривленную сингулярность вокруг горизонта Коши, заблокировав путь область, допускающую путешествия во времени, фактически закрыв дорогу в другие вселенные и в будущее.

Но такая сингулярность, расположенная вдоль горизонта Коши, может быть слабой. Согласно расчетам Амоса Ори, приливные силы, вполне возможно, и не разорвут вас. Приливные силы могут возрастать до бесконечности, однако просуществовать лишь в течение исчезающе краткого периода. Аспирант может обнаружить, что тело его не растянулось до бесконечности (не спагеттифицировалось), а лишь удлинилось на дюйм, как после визита к мануальному терапевту. Еще одна неизвестность сопряжена с тем, что горизонт Коши может оказаться нестабильным: флуктуации на нем могут возрастать, выбрасывая часть решения за пределы этого горизонта в новых непредсказуемых направлениях. Один из факторов в пользу аспиранта заключается в том, что мы не знаем законов квантовой гравитации, то есть не знаем, как гравитация действует на микромасштабах. Керровское решение эйнштейновских уравнений общей теории относительности не учитывает квантовых эффектов. Считается, что на микромасштабах квантовые эффекты должны быть важны и под их действием сингулярности должны размазываться. Именно благодаря этим эффектам аспиранту, возможно, удастся проскочить. Но поскольку мы не знаем законов квантовой гравитации, мы не можем знать наверняка, что именно произойдет. Когда у нас будет теория Великого Объединения для физики частиц, нам, возможно, удастся ответить на этот вопрос. Тем временем вращающаяся черная дыра еще скрывает кое-какие секреты. Один из способов их разгадать – прыгнуть прямо в эту дыру!

Теперь вернемся к струнной петле, которая упала в черную дыру и таким образом превратилась в машину времени. Горизонт Коши для путешествий во времени вокруг струн, найденный Катлером, будет совпадать с горизонтом Коши образующейся при этом вращающейся керровской черной дыры. Стоит вам пересечь горизонт Коши – и вот вы уже в области, где возможны хронопутешествия. У нас нет точных решений для случая со схлопывающейся струнной петлей, которыми можно было бы руководствоваться, но интересно, что в 1999 году Сёрен Хольст и Ханс-Юрген Мачулл нашли точное решение для аналогичного случая с меньшим количеством измерений (плоского), где две частицы (с конической внешней геометрией – точно как у космических струн) на высокой скорости проходят одна мимо другой в искривленном пространстве-времени и порождают машину времени, запертую во вращающейся черной дыре!

Говоря о случае со струнными петлями, нужно рассмотреть несколько потенциальных возможностей. Может быть, удастся обойти по кругу космическую струнную петлю и вернуться назад, обменявшись рукопожатиями со своим более молодым двойником, но при этом вы окажетесь в черной дыре и, следовательно, никогда не сможете вернуться назад и рассказать о своих приключениях. Затем вы можете погибнуть, врезавшись в сингулярность. Если вам по-настоящему повезет, то вы можете вынырнуть в новой Вселенной, однако вернуться к друзьям вы все равно не сможете. Хуже того, вы можете погибнуть от контакта с сингулярностью еще до того, как откроется возможность путешествий во времени. Неизвестно, какой из этих сценариев произойдет в реальности.

Стивен Хокинг доказал, что если горизонт Коши для путешествий во времени возникает в конечной области, а плотность материи никогда не становится отрицательной, то где-то на горизонте Коши должна образоваться сингулярность. В принципе, это теорема, согласно которой сложно сконструировать машину времени из обычной материи у себя в гараже, если лишь слегка искривить пространство-время (не допуская возникновения сингулярности). В случае, когда две бесконечные струны проходят одна мимо другой, плотность энергии в любой точке всегда остается неотрицательной, но поскольку струны бесконечны, горизонт Коши также простирается до бесконечности, и теорема Хокинга оказывается неприменимой. Однако в случае с решением, описывающим замкнутые конечные струнные петли, где действительно допускается возможность создания машины времени, можно считать, что внутри черной дыры на горизонте Коши должна образоваться сингулярность. Она не обязательно должна преградить вам путь, но вы хотя бы увидите ее вдалеке, как только пересечете горизонт Коши. Однако если горизонт Коши заключен внутри черной дыры (подозреваю, что так и есть), а черная дыра испарится под действием хокинговского излучения (что неизбежно), то квантовое вакуумное состояние вне черной дыры приобретет слегка отрицательную плотность энергии (и из-за этого горизонт событий начнет сужаться), что, опять же, означает неприменимость теоремы Хокинга. Таким образом, не потребуется нарушать никакие теоремы, чтобы создать машину времени, заключенную во вращающейся черной дыре, где вы не погибаете от столкновения с сингулярностью, до того как пересечете горизонт Коши.

Поскольку черная дыра успевает испариться за конечный период времени, это означает, что вы, приближаясь к горизонту Коши, не увидите всей истории Вселенной, пока не пересечете его (но именно это произойдет перед тем, как горизонт событий черной дыры в результате ее испарения сожмется до нулевого размера). Следовательно, пока вы будете падать в черную дыру, вас не будут беспорядочно бомбардировать фотоны, сильно смещенные в синюю часть спектра. Это тоже неплохо.

Горизонт Коши нестабилен; однако ведь у нас есть истребители, которые также нестабильны в воздухе, но под управлением летчика приобретают удивительную маневренность. Аналогичный пример – фокус с длинным карандашом, который ставишь носиком себе на подушечку пальца и быстро двигаешь пальцем, не давая карандашу упасть. Жонглеры постоянно проделывают такие трюки с першами. В принципе, сверхцивилизация может научиться стабилизировать горизонт Коши, активно возмущая его нужным образом.

Если вы решите слетать в прошлое на год назад, единожды обогнув схлопывающуюся струнную петлю (внутри черной дыры), то для этого потребуется найти струнную петлю, масса которой всего раза в два меньше, чем у нашей Галактики. Лишь сверхцивилизации могут хотя бы попытаться воплотить такой проект.

Погибнете ли вы перед перемещением во времени? Выживете ли и сможете ли слетать к событию из собственного прошлого, и все это – в пределах вращающейся черной дыры? Чтобы ответить на эти вопросы, нам потребуется окончательно разобраться в законах квантовой гравитации – понять, каким образом гравитация проявляется на микромасштабах. Вот еще одна причина, по которой эта проблема столь интересна.

Движение космических струн не единственное решение эйнштейновских уравнений общей теории относительности, допускающее путешествия во времени. Первое решение было связано с нерасширяющейся, но вращающейся Вселенной. Его предложил в 1949 году знаменитый математик Курт Гёдель. Хотя на самом деле наша Вселенная расширяется, а не вращается, решение Гёделя показало, что общая теория относительности в принципе допускает путешествия в прошлое. Если существует одно такое решение, значит, могли обнаружиться и другие. В 1974 году Франк Типлер продемонстрировал, что путешествие в прошлое можно организовать при помощи бесконечно высокого вращающегося цилиндра. В 1988 году Кип Торн и его коллеги Майк Моррис и Ульви Уртсевер предложили модель машины времени на базе проходимой кротовой норы. В общей теории относительности кротовой норой называется короткий туннель, соединяющий две далекие точки в искривленном пространстве-времени. Проходимой называется такая кротовая нора, которая остается распахнутой достаточно долго, чтобы через нее можно было проскочить (в отличие от кротовой норы с диаграммы Крускала, с которой мы познакомились в главе 20). Насколько мы понимаем общую теорию относительности, такие туннели могут существовать, хотя ни один подобный объект пока не открыт. Один выход из туннеля может располагаться возле Земли, а другой – у альфы Центавра, в четырех световых годах отсюда. Однако длина самого туннеля может не превышать трех метров (рис. 21.7).

Если отправить луч света от Земли к альфе Центавра, то свет будет лететь туда четыре года. Но можно проскочить через кротовую нору – и оказаться у альфы Центавра через считаные секунды. Таким образом, можно обогнать луч света, летящий к альфе Центавра, срезав путь через кротовую нору. Как может выглядеть вход в кротовую нору, иными словами, ее устье? На схеме оно напоминает круг, но ведь эта схема учитывает всего два измерения. На самом деле устье кротовой норы имеет форму шара. Оно выглядит примерно как те блестящие зеркальные шары, которые иногда доводится видеть в саду. Это явление верно изображено в фильме «Интерстеллар», на съемках которого Кип Торн работал научным консультантом по физике. Но не думайте, что в кротовой норе отразится ваш земной сад. Вместо этого вы увидите сад с планеты, вращающейся в системе альфы Центавра. Прыгайте в этот шар на Земле и выныривайте из него где-нибудь у альфы Центавра.

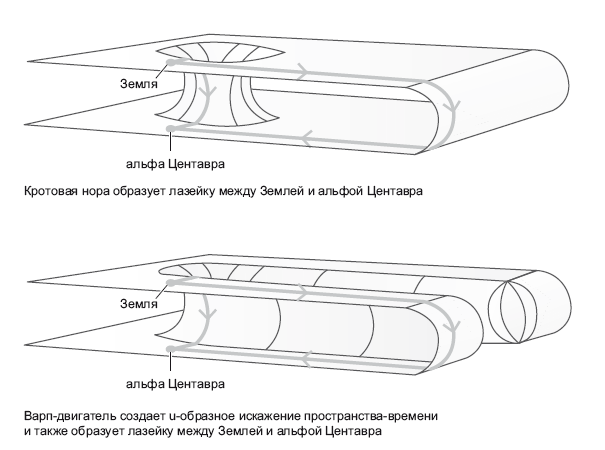
Рис. 21.7. Кротовые норы и варп-двигатели. Иллюстрация предоставлена Дж. Ричардом Готтом, адаптирована из Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

Вот как можно превратить кротовую нору в машину времени. Предположим, мы нашли такую кротовую нору 1 января 3000 года. Если взглянуть через нее, то увидишь систему альфы Центавра, но в какое время? Если два устья (выхода из туннеля) синхронизированы, то часы в системе альфы Центавра также будут установлены на 1 января 3000 года. Никакого путешествия во времени не происходит. Но теперь предположим, что мы подводим к кротовой норе массивный космический корабль и гравитационно оттягиваем устье кротовой норы, расположенное поблизости от Земли, на 2,5 световых года вперед и обратно, причем устье движется со скоростью 99,5 % от скорости света. Землянам покажется, что такой путь туда и обратно займет всего 5 лет, и устье кротовой норы вновь окажется около Земли 10 января 3005 года.

Допустим, в центре туннеля кротовой норы сидел астронавт. Он будет стариться вдесятеро медленнее вас, поскольку двигался со скоростью 99,5 % от скорости света. За время путешествия он состарится всего лишь на десятую часть от 5 лет, то есть на полгода. Когда он вернется, у него на часах будет 1 июля 3000 года. Но длина туннеля кротовой норы составляет всего 3 метра. За время путешествия длина туннеля не изменяется, поскольку его геометрия зависит от вещества, расположенного в туннеле кротовой норы, а это вещество не изменилось. Более того, астронавт находится в состоянии покоя относительно устья, обращенного к альфе Центавра, а само это устье стационарно относительно альфы Центавра, поскольку с той стороны никакого движения не происходит. Часы астронавта должны оставаться синхронизированными со временем альфы Центавра. Если вы заглянете в кротовую нору по возвращении астронавта и увидите, что у него на часах сейчас 1 июля 3000 года, то расположенные у него за спиной часы из системы альфа Центавра также должны показывать 1 июля 3000 года. Следовательно, когда устье кротовой норы возвращается к Земле 10 января 3005 года, вы можете заглянуть в нее и увидеть часы из системы альфы Центавра, которые в этот момент будут показывать 1 июля 3000 года. Уже понимаете, какая возможность перед вами открывается. Прыгаете через кротовую нору и оказываетесь в системе альфы Центавра 1 июля 3000 года. Садитесь на космический корабль и возвращаетесь к Земле на скорости 99,5 % от скорости света. Ваш путь через обычное пространство займет чуть более 4 лет, вы вернетесь на Землю 8 июля 3004 года. Но вы отправились в путь 10 января 3005 года, то есть вы вернулись домой раньше, чем улетели. Поэтому вы можете поучаствовать в событиях собственного прошлого. Пожать руку себе же 8 июля 3004 года, еще до начала пути. Обратите внимание: через кротовую нору можно попасть в прошлое, но не раньше того момента, в который была создана машина времени, то есть той даты, когда от Земли стали оттягивать расположенное близ нее устье кротовой норы. Так, нельзя уйти в прошлое к дате ранее 3000 года, поскольку в это время еще не были рассинхронизированы два устья кротовой норы.

Направление этим исследованиям было задано Карлом Саганом. Он написал научно-фантастический роман «Контакт», в главе 10 Нил рассказывал вам о фильме по этому роману. По замыслу Сагана, героиня романа, которую в кино играет Джоди Фостер, должна была прыгнуть в кротовую нору и оказаться рядом с Вегой – звездой, удаленной от нас на 25 световых лет. Карл хотел, чтобы эпизод получился корректным с точки зрения физики, и позвонил своему другу Кипу Торну. Торн с коллегами исследовали физику кротовин и пришли к выводу, что кротовые норы должны быть начинены веществом, обладающим отрицательной энергией, то есть таким веществом, энергия которого меньше нуля, и которому присуща отталкивающая гравитация. Свет сходится к кротовой норе, проникает сквозь ее туннель и рассеивается с другой стороны. Это характерное проявление гравитационного отталкивания, свойственного объектам, обладающим отрицательной энергией. Как вы помните, на диаграмме Крускала кротовая нора сопутствовала черной дыре, но перебраться через нее на другую сторону дыры было нельзя. Вы не могли проникнуть в другую вселенную, минуя сингулярность, а при столкновении с сингулярностью вас разрывало на куски. Но если у вас будет материя, обладающая отрицательной энергией, то открытую кротовую нору удастся стабилизировать и перейти через нее на ту сторону. Но где же взять материю, обладающую отрицательной энергией?

Любопытно, что известен квантовый эффект, так называемый «эффект Казимира», при котором наблюдается материя с отрицательной энергией. Если поместить почти вплотную друг к другу две металлические проводящие пластины, то квантовое состояние вакуума между этими пластинами будет обладать отрицательной плотностью энергии. Давление, связанное с эффектом Казимира, было зафиксировано в лабораторных экспериментах, поставленных в лаборатории М.Й. Спарнаэем и С.К. Ламоро. Квантовое состояние вакуума Хартле – Хокинга, возникающее вокруг черной дыры, также обладает слегка отрицательной плотностью энергии, что позволяет черной дыре со временем испариться. При таком испарении площадь горизонта событий уменьшается. Два этих примера демонстрируют, что получить материю с отрицательной энергией возможно. Торн с коллегами выяснили, что если установить в туннеле кротовой норы две сферические пластины выпуклыми сторонами друг к другу, так, чтобы они перекрывали туннель и расстояние между ними не превышало 10^–10 см, то возникающий между ними эффект Казимира должен удержать кротовую нору от схлопывания. Вам останется открыть люки в пластинах – и пройти. (Поскольку все эти варианты сопряжены с такой материей, которая обладает отрицательной энергией, «кротовонорные» решения позволяют создать машину времени в конечной области без возникновения сингулярности, так как теорема Хокинга в данном случае не работает – о чем мы уже упоминали ранее.)

В такой машине времени, которую предложили Торн с коллегами, каждое устье кротовой норы должно весить 100 миллионов солнечных масс и иметь радиус в 1 а.е. Создание такой кротовой норы – масштабный проект, за который могла бы взяться лишь сверхцивилизация. Единственный способ реализовать подобное – найти два микроскопических устья квантовой кротовой норы, удаленные друг от друга на 1,6 ? 10^–33 см, диаметром также 1,6 ? 10^–33 см, входящие в состав пространственно-временной квантовой пены, которая, как считается, заполняет микромир. Затем два этих устья потребовалось бы медленно отвести в разные стороны и постепенно нарастить, пока каждое не стало бы весить 100 миллионов солнечных масс. Такие проекты в гараже не делаются! Но недавние работы Малдасены и Сасскинда показывают, что на свете могут существовать микроскопические квантовые кротовые норы, соединяющие частицы, находящиеся в состоянии запутанности, – значит, у нас есть хотя бы отправная точка.

Другая знаменитая модель машины времени – это варп-двигатель, описанный в сериале «Звездный путь». Такой двигатель создает U-образное искажение пространства, которое также позволяет мгновенно преодолевать большие расстояния – например, до альфы Центавра. Это не дыра, а всего лишь U-образное искажение (см. рис. 21.7). Физик Мигель Алькубьерре рассмотрел этот феномен с точки зрения общей теории относительности и обнаружил, что для работы варп-двигателя требуется как вещество с положительной, так и вещество с отрицательной энергией, но теоретически он реализуем.

Недавно Амос Ори предложил модель тороидальной машины времени (напоминающей по форме бублик). Ученые до сих пор открывают новые творческие решения общей теории относительности, связанные с путешествиями во времени.

Стивен Хокинг полагает, что некоторые еще не открытые квантовые эффекты могут «запретить» путешествия во времени, пусть даже такие путешествия допускаются в общей теории относительности. Он выдвинул «гипотезу о защите хронологии», согласно которой законы физики должны каким-то образом исключать путешествия в прошлое. Он обосновал эту гипотезу некоторыми свидетельствами о том, что квантовое состояние вакуума может стать бесконечным при приближении к горизонту Коши и той области, в которой возможны хронопутешествия. Мы с Ли-Синь Ли нашли контрпример, в котором складывалось иное квантовое состояние вакуума, не достигавшее бесконечности на горизонте Коши. Ученик Хокинга Майкл Дж. Кэссиди пришел к аналогичному выводу, но путем иных умозаключений. Итак, представляется, что в некоторых ситуациях путешествия во времени возможны. Опять же, чтобы судить об этом наверняка, нужно определить законы квантовой гравитации.

В 1895 году, когда Уэллс опубликовал роман «Машина времени», известные на тот момент законы (ньютоновской) физики предполагали, что везде одинаково течет общепринятое время, и путешествия в прошлое или будущее не допускались. Но спустя всего 10 лет, в 1905 году, Эйнштейну предстояло доказать, что путешествия в будущее возможны. Космонавт Геннадий Падалка уже улетел в будущее на 1/44 секунды (см. главу 18). В 1915 году Эйнштейн сформулировал теорию гравитации, действующую в искривленном пространстве-времени и описывающую, как можно обогнать луч света; следовательно, такая теория открывала путь к путешествиям в прошлое. Сегодня уже известны несколько решений эйнштейновских уравнений, в принципе допускающих путешествия в прошлое. В настоящее время мы находимся в совершенно противоположной ситуации, чем Уэллс в период написания своего знаменитого романа. Общая теория относительности Эйнштейна, до сих пор выдерживавшая все испытания, которым ее подвергали, – это лучшая имеющаяся у нас теория тяготения, и у нее есть решения, в принципе, допускающие путешествия во времени, пусть даже ресурсами для таких путешествий может располагать лишь сверхцивилизация. Известно, как действует гравитация в макроскопических масштабах, а также известно, что на микромасштабах становится важен вклад квантовых эффектов, так что по-прежнему необходимо разрабатывать теорию квантовой гравитации. Мы должны успешно поженить общую теорию относительности и квантовую механику, сложив из них работоспособную теорию, и понять, возможно ли сконструировать машину времени, позволяющую слетать в прошлое. Насколько мы можем судить сегодня, законы физики, в принципе, допускают путешествия в прошлое, но пока открыт другой вопрос: не запрещены ли такие путешествия какими-то другими законами физики, которые еще только предстоит открыть.

В своей книге «Путешествия во времени в эйнштейновской Вселенной» (Time Travel in Einstein’s Universe, 2001) я исследовал идеи специальной и общей теории относительности применительно к возможности путешествий во времени. Действительно, общая теория относительности изучает путешествия в прошлое, но не с целью сконструировать машину времени в настоящем, а для того, чтобы понять устройство Вселенной. Решения, допускающие путешествия во времени, – это проверка законов физики в экстремальных условиях. В главе 23 я вернусь к теме путешествий во времени, когда мы станем обсуждать условия, сложившиеся в новорожденной Вселенной.