Книга: Большое космическое путешествие

Глава 20 Черные дыры

Глава 20

Черные дыры

Автор: Дж. Ричард Готт

Эта глава посвящена самым таинственным объектам во Вселенной – черным дырам. Одно из первых точных решений, удовлетворявшее эйнштейновским уравнениям общей теории относительности, соответствовало черной дыре. Точное решение эйнштейновских уравнений – это пространство-время, чья геометрия в каждой точке характеризуется кривизной, и в каждой точке этого пространства-времени уравнения решаются локально. Особенно интересно решение для геометрии пустого пространства, окружающего точечную массу. Здесь мы говорим о вакуумных уравнениях поля, поскольку эти уравнения применимы к пустоте. Именно эти уравнения пытался решить Эйнштейн, исследуя орбиту Меркурия и искривление света в вакууме поблизости от Солнца. Но найти такое решение было сложно, поскольку никто не представлял, какова должна быть его геометрия, так что Эйнштейн удовлетворился приблизительным решением. В рамках этого решения он предполагал, что пространство-время приблизительно плоское, как и в специальной теории относительности, но с небольшими возмущениями (отклонениями от идеально плоской формы). Решать уравнения для небольших возмущений оказалось проще, поскольку уже было известно, какова должна быть исходная геометрия и, отталкиваясь от нее, было удобнее находить решения с учетом небольших поправок. Поскольку скорости объектов, вращающихся вокруг Солнца, невелики по сравнению со скоростью света, околосолнечное пространство лишь слегка искривлено. Поэтому приблизительное решение Эйнштейна оказалось достаточно точным, равно как и спрогнозированные им величины для орбиты Меркурия и искривления света около Солнца. Возможно, Эйнштейн считал, что найти точные решения для этих уравнений будет слишком сложно. Так или иначе, он остановился на приблизительном.

Первым, кому удалось найти точное решение для эйнштейновских уравнений поля в вакууме вокруг точечной массы, был немецкий астроном Карл Шварцшильд. Он обнаружил решение, описывавшее черную дыру, то есть точечный источник гравитации в абсолютной пустоте. Публикуя работы по общей теории относительности, Эйнштейн прикидывал, что в мире найдется примерно дюжина человек, способных ее понять. Одним из них был Карл Шварцшильд. В 1900 году он написал статью о возможной кривизне пространства. Это было еще до появления специальной теории относительности. Он рассуждал, что пространство может обладать положительной кривизной, подобно шару, либо отрицательной кривизной, как у ковбойского седла. Шварцшильд хотел выяснить, каков должен быть радиус этой кривизны с учетом наиболее актуальных на тот момент астрономических наблюдений. Уже тогда он стремился исследовать кривизну пространства. Когда вышла статья Эйнштейна, Шварцшильд очень живо откликнулся на нее: понял эту статью и, что не менее важно, оказался способен справиться со сложной математикой, присущей тензорам кривизны Римана. Он оказался во всеоружии, чтобы извлечь из этих данных что-то новое и оригинальное. Шварцшильду удалось решить задачу, поскольку он стал решать эти уравнения в очень толковой системе координат, позволявшей воспользоваться следующим фактом: задача связана со сферической симметрией и неизменна во времени. Оказалось, что такое решение эйнштейновских уравнений для точечной массы в пустом пространстве описывает внешнюю часть черной дыры.

На Первой мировой войне Карл Шварцшильд подхватил редкое аутоиммунное заболевание, в то время смертельное; в 1916 году он был комиссован по болезни, уже дома узнал о статье Эйнштейна и нашел свое решение. Он отправил решение Эйнштейну, сообщив, что в разгар войны был счастлив «провести некоторое время в саду ваших идей». Через пару месяцев Шварцшильд умер.

Найти такое точное глобальное решение для вакуумных уравнений поля было сложно, как сшить лоскутное одеяло. В каждой точке пространства сшиваем кусочки, и локальные члены кривизны повсюду отличаются, но в сумме они дают ноль. Эти уравнения диктуют правила, по которым можно сшивать лоскуты. Просто шьешь и добавляешь кусочек за кусочком. Но, в конечном итоге, у тебя должно получиться глобальное решение – лоскутное одеяло, – каждая точка которого удовлетворяет этим уравнениям. Это довольно сложно. Карл Шварцшильд оказался одним из первых, кому удалось найти такое решение для искривленного пространства вокруг точечной массы.

Сын Карла Шварцшильда Мартин долгое время работал в Принстоне и был нашим коллегой (см. рис. 8.3). Он также стал астрономом и внес серьезный вклад в науку. Так, Мартин определил, что такие звезды, как Солнце, рано или поздно становятся красными гигантами. Он определенно пошел по стопам отца, которого, в сущности, и не знал – тот умер, когда Мартину было всего 4 года. Интересно, что Карл в Первую мировую войну сражался за Германию, а Мартин бежал из Германии после того, как к власти пришел Гитлер, и во Вторую мировую войну выступал против Германии на стороне США.

Чтобы понять, что такое черные дыры, для начала вернемся к ньютоновскому тяготению. Если я возьму мяч и подброшу в воздух, то что произойдет? Мяч немного взлетит, а затем упадет. Есть даже пословица: «Чем выше взлетишь, тем больнее падать». Правда, вот незадача: эта пословица ошибочна. Если не учитывать сопротивление воздуха, то можно кинуть мяч с достаточной скоростью, превышающей вторую космическую, например 40 000 км/ч, – тогда мяч преодолеет земную гравитацию и никогда не упадет. Астронавты «Аполлона» летели к Луне практически на такой скорости. В теории Ньютона есть формула для расчета такой скорости убегания: v_уб² = 2GM/r, где G – ньютонова гравитационная постоянная, M – масса Земли, а r – радиус Земли. Теперь допустим, что у меня есть колоссальный пресс для мусора, при помощи которого я сжал Землю в малюсенький шарик, как будто она бумажная; в таком случае ее радиус уменьшится. Что произойдет со скоростью убегания? Масса Земли останется прежней, а радиус станет гораздо меньше, поэтому скорость, необходимая для отрыва от поверхности, возрастет. В конце концов я могу спрессовать Землю настолько сильно, что вторая космическая скорость сравняется со скоростью света c. Насколько мал должен быть такой радиус? Можно просто подставить в уравнение член v_уб² = c² = 2GM/r и вычислить r. Получится, что r = 2GM/c². Эта величина называется «радиус Шварцшильда» в честь Карла Шварцшильда. При такой массе, как у Земли, радиус Шварцшильда равен 8,8 мм. Это размер крупной жемчужины. Если сжать Землю до еще меньшего радиуса, то вторая космическая скорость станет выше скорости света, и ничто, даже свет, с Земли улететь не сможет. Эйнштейн продемонстрировал, что превысить скорость света невозможно, поэтому если сплюснуть Землю до размеров менее радиуса Шварцшильда, то планета необратимо превратится в черную дыру. Мы называем ее «черной дырой», поскольку никакого света от нее не отражается. Масса, заключенная в черной дыре, будет и далее сжиматься все сильнее и сильнее, вторая космическая скорость продолжит расти. В пределах радиуса Шварцшильда гравитация превосходит все остальные силы, и вся масса сжимается в точку, в сингулярность с бесконечной кривизной в центре. Согласно теории относительности, размер такой точки должен быть нулевым, но считается, что под действием квантовых эффектов сингулярность размажется до размера около 1,6 ? 10^–33 сантиметров, так называемой планковской длины (в главе 24 будет рассказано, откуда берется это число). Эта величина гораздо меньше атомного ядра. В итоге имеем в центре точечную массу (сосредоточенную фактически в нулевом объеме), а вокруг нее – пустое искривленное пространство.

Если бы мы вошли в пределы радиуса Шварцшильда, то смогли бы мы выбраться обратно? Нет. Для этого потребовалось бы развить сверхсветовую скорость, а Эйнштейн продемонстрировал, что это невозможно.

Радиус Шварцшильда черной дыры пропорционален ее массе. Чем больше масса, тем шире будет радиус Шварцшильда. Истина такова, что Землю было бы очень сложно сжать до радиуса Шварцшильда. Но когда массивная звезда сжигает все свое ядерное топливо, от нее остается плотное ядро, которое вполне может уменьшиться до собственного радиуса Шварцшильда. Когда Солнце погибнет, оно превратится в красный гигант, потом от него отделятся газовые оболочки и останется ядро – белый карлик размером примерно с Землю. Если масса звездного ядра окажется больше 1,4 солнечных масс, но не превысит 2 солнечных, то белый карлик будет сжиматься и дальше, пока не превратится в нейтронную звезду радиусом около 12 километров. Нейтронная звезда всего в 2–3 раза крупнее своего радиуса Шварцшильда, поэтому она близка к опасному пределу. Если же попытаться сформировать нейтронную звезду, которая будет немного тяжелее 2 солнечных масс, то получится нестабильный объект, который может сконцентрироваться в пределах радиуса Шварцшильда, – тогда гравитация полностью возобладает и возникнет черная дыра. Черная дыра в 10 солнечных масс, какая может образоваться в итоге гибели и коллапса очень массивной звезды, имеет радиус Шварцшильда 30 километров. У сверхмассивной черной дыры в 4 миллиона солнечных масс – такая черная дыра находится в центре нашей Галактики – радиус Шварцшильда равен 12 миллионам километров (чуть менее 1/10 а.е.). Одна из крупнейших когда-либо обнаруженных черных дыр находится в центре гигантской эллиптической галактики М87. Ее масса – 3 миллиарда солнечных и, соответственно, ее радиус равен 9 миллиардам километров. Эта величина вдвое больше радиуса всей Солнечной системы с учетом орбиты Нептуна.

Предположим, мы отправились за шварцшильдовский радиус в черную дыру, чья масса – 3 миллиарда солнечных. Допустим, в опыте участвуют профессор и аспирант; профессор хочет узнать, что происходит внутри, и посылает аспиранта на разведку. Профессор остается в ракете за пределами черной дыры и зависает на постоянной высоте, равной, скажем, 1,25 радиуса Шварцшильда. Профессор ощущает ускорение, обусловленное работой двигателей ракеты, которая должна оставаться на этом фиксированном расстоянии от черной дыры и не падать в нее. Пока профессор держится за пределами черной дыры, ничего дурного с ним не происходит. Однако отважный аспирант, чтобы исследовать черную дыру, просто пускается в свободное падение. ВЖУУУУУХ! Падая, аспирант радирует профессору и сообщает, как идут дела. Первый информационный фрагмент – слово «ДЕЛА». Радиосигнал летит прочь от аспиранта со скоростью света.

Тем временем аспирант продолжает падать, а радиосигнал достигает профессора. Он получает первое слово из сообщения: «ДЕЛА». Аспирант, падая, посылает второе слово из сообщения: «ИДУТ». Это слово было отправлено буквально на кромке радиуса Шварцшильда. Этот сигнал также улетает прочь со скоростью света, но ему требуется больше времени, чтобы достичь профессора. Профессор вынужден жечь топливо, просто чтобы оставаться на месте и не упасть в дыру, так что фактически он все время ускоряется в сторону от горизонта, и сигнал «ИДУТ» догоняет его довольно нескоро.

Тем временем аспирант пересекает радиус Шварцшильда. Это хорошо? К сожалению, нет. При этом он проходит точку невозврата, но никакого «дорожного знака» о такой точке не заметит. Здесь с аспирантом не произойдет ничего интересного. Ему кажется, что все нормально. На самом деле, прямо сейчас вы можете пересекать радиус Шварцшильда какой-нибудь колоссальной черной дыры, и с вашей комнатой, где вы читаете эти строки, ничего не случится. Крохотный участок пространства-времени локально кажется практически плоским, поэтому локальные измерения абсолютно не позволяют судить, каково глобальное решение. Миновав радиус Шварцшильда, аспирант посылает третье слово: «ДОСТАТОЧНО». Второе слово, «ИДУТ», по-прежнему летит к профессору. Пока профессор получил только слово «ДЕЛА». Итак, аспирант оказался в пределах радиуса Шварцшильда. Сигнал «ДОСТАТОЧНО» удаляется от него со скоростью света. Но этот сигнал подобен ребенку, бегущему вверх по эскалатору, идущему вниз – без всякого толку. На радиусе Шварцшильда вторая космическая скорость равна скорости света; радиосигнал, летящий со скоростью света, навечно остается на этом радиусе и дальше улететь не может. Сигнал «ИДУТ» продолжает путь прочь от черной дыры.

Пока аспирант продолжает падать все дальше в глубь радиуса Шварцшильда, начинает происходить что-то странное. Он падает ногами вперед. То есть ноги ближе к центру черной дыры, чем голова. Поскольку гравитация – это сила, пропорциональная 1/r², ноги испытывают более сильное тяготение, нежели голова, а на поясе аспиранта тяготение примерно среднее. Голова и ноги тянутся в разные стороны из-за этого приливного взаимодействия. Аспиранта как будто вздергивают на дыбе. Кроме того, его плечи все плотнее сжимает с боков по мере того, как сближаются линии, идущие от них к центру черной дыры. Аспиранта расплющивает, словно в «железной деве». Аспирант успевает отправить последнее слово: «ПЛОХО». Получается «ДЕЛА ИДУТ ДОСТАТОЧНО ПЛОХО».

Он приближается к центру, и силы все возрастают. Аспиранта так растягивает от головы до пят и сдавливает с боков, что он словно превращается в макаронину. Это явление называется «спагеттификация». Да, это самый настоящий научный термин, которым астрономы именуют такой процесс! В конце концов аспиранта раздавит и разорвет, и его останки упокоятся в центре черной дыры. Теперь эта центральная масса весит как 3 миллиарда Солнц и еще чуточку! Радиус Шварцшильда немного расширяется. Сигнал «ИДУТ» все еще пробивается к профессору. Сигнал «ДОСТАТОЧНО» никуда не двигается с радиуса Шварцшильда. Сигнал «ПЛОХО» летит наружу со скоростью света, но он похож на ребенка, бегущего вверх по нисходящему эскалатору: как ни старается ребенок, его все равно тянет вниз. Сигнал, конечно, стремится к краю дыры, но его затягивает к центру, где сигнал расплющивается и также оказывается в сингулярности.

Наконец, спустя значительное время, профессор наконец-то получает сигнал «ИДУТ». Он принял информацию «ДЕЛА И-Д-У-Т». Он никогда не получит остаток сообщения «ДОСТАТОЧНО ПЛОХО». Слово «ДОСТАТОЧНО» застряло на радиусе Шварцшильда, а слово «ПЛОХО» черная дыра затянула в точечную центральную сингулярность, и аспиранта туда же. «ПЛОХО» – это описание события, которое произошло в пределах радиуса Шварцшильда. Сигнал так и не добирается до профессора, и профессор никогда не узнает, что происходит внутри этого радиуса. Профессор не в состоянии увидеть ни одного события, происходящего за радиусом Шварцшильда, поэтому сфера с таким радиусом называется «горизонт событий». Это граница той части пространства, где происходят события, заметные профессору. Горизонт событий для профессора попросту непроницаем. Аналогично, на Земле мы не можем заглянуть за линию горизонта: эта линия – предел поля видимости. Любой наблюдатель, находящийся за пределами горизонта событий черной дыры, никогда не увидит событий, происходящих внутри этого горизонта.

Если профессор заинтересуется, что произошло с бедным аспирантом, он может заглушить двигатели ракеты, державшие его на кромке черной дыры, и самостоятельно отправиться в свободное падение. Достигнув горизонта событий, он получит застрявший там сигнал «СОВСЕМ». Скатываясь вниз по эскалатору, он заметит, как сигнал «СОВСЕМ» минует его со скоростью света. Свет всегда будет лететь мимо профессора со скоростью 300 000 км/c. Но затем профессор упадет в центр черной дыры и также погибнет.

Если аспирант попадет в черную дыру, которая в 3 миллиарда раз тяжелее Солнца, то, пока он будет падать до центра, где и погибнет, у него на часах пройдет 5,5 часа. К счастью, процесс спагеттификации, с того момента, как приливные силы станут болезненными и в итоге разорвут его на части, займет 0,09 секунды в самом конце пути. По крайней мере, его ждет быстрая смерть.

Возможно, нас также заинтересует, какова искривленная геометрия внешней границы черной дыры. Однажды меня пригласили на передачу «Час новостей с Мак-Нилом и Лерером», так как астрономы, работающие с телескопом «Хаббл», как раз открыли, что в галактике М87 существует черная дыра. Поэтому ведущие хотели, чтобы мы с Кипом Торном объяснили зрителям этот феномен. Я привел небольшой наглядный пример. Если построить плоскость, проходящую через центр черной дыры, то логично предположить, что эта плоскость должна быть ровной и двумерной как баскетбольная площадка, а радиус Шварцшильда должен ограничивать круг, напоминающий линию штрафного броска. Сингулярность – точка в центре такого круга. Но на самом деле все не так. Плоский сегмент, проходящий через центр черной дыры, на самом деле искривлен. Он похож на раструб, направленный вверх (рис. 20.1). Третье измерение здесь добавлено лишь для того, чтобы вы могли оценить кривизну двумерной воронкообразной поверхности. Третье измерение в данном случае иллюзорно. Забудьте о пространстве над воронкой и под ней, в данном случае реален лишь сам профиль воронки. На больших расстояниях раструб уплощается, поэтому в самом деле начинает походить на ровную баскетбольную площадку. Вдали от дыры кривизна невелика. Чем ближе вы к дыре, тем круче внутренняя поверхность раструба срывается в воронку. На радиусе Шварцшильда склон становится отвесным. Радиус Шварцшильда соответствует самой узкой окружности на поверхности раструба. Вот почему феномен называется «черная дыра» – это и есть дыра. На самом деле, в системе координат, изобретенный Карлом Шварцшильдом, радиальная координата rназывается окружным радиусом и определяется не как расстояние до центра, а по длине соответствующей окружности, которая должна быть равна 2?r. Окружности принадлежат поверхности воронки. А саму воронку можно рассматривать как последовательность сужающихся окружностей, наименьшая из которых расположено на дне воронки (ее длина равна 2? радиуса Шварцшильда). Радиус Шварцшильда – это радиус окружности, ограничивающей отверстие на дне воронки (не обращайте внимания на круглую основу с рис. 20.1 – она просто поддерживает воронку).

На телетрансляции я воспользовался в качестве наглядного пособия воронкой, напоминающей раструб. Я поставил ее так, чтобы «юбка» оказалась сверху, а узкий конец – снизу (см. рис. 20.1). Астрономы обнаружили, что вокруг черной дыры в галактике M87 с огромной скоростью вращается газ. Чтобы показать, как это происходит, я сбоку бросал бусинки в воронку, чтобы они по спирали медленно скатывались в отверстие, а потом исчезали там. Газ аналогичным образом вращается вокруг дыры, причем чем ближе к дыре молекулы газа, тем быстрее они вращаются. Между молекулами газа возникает трение. Из-за трения газ нагревается и начинает светиться. Это излучение можно наблюдать, поскольку оно возникает вне горизонта событий. При сиянии выделяется энергия, и газ, теряя энергию, соскальзывает в дыру. Именно таков источник сияния квазаров: там светится газ, по спирали сливающийся в массивную черную дыру. Мы видим горячий газ, когда он по спирали несется к горизонту событий, но он исчезает из виду, как только пересекает этот горизонт. Я тренировался все это показывать и уже счел, что демонстрация получилась наглядной (и уже можно снимать новостной сюжет). Затем я все показал дочке, которой тогда было семь, и она предложила: «Почему бы не сбросить туда астронавта»?

Рис. 20.1. Воронка черной дыры. Пространство вокруг черной дыры не плоское, как баскетбольная площадка, а искривлено подобно воронке. На радиусе Шварцшильда воронка становится отвесной. Это место обозначено красной полоской, имеющей длину 2? радиуса Шварцшильда. Астронавт может падать прямо в черную дыру. Когда он достигает радиуса Шварцшильда (красная полоска) – это точка невозврата. Не обращайте внимания на круглую основу, на которой стоит воронка. Также не обращайте внимания на то, что у нашей воронки есть внешняя и внутренняя поверхность; в данном случае реален лишь профиль воронки. Снимок предоставлен Дж. Ричардом Готтом

Она сходила к себе в комнату и вернулась с милым астронавтом «Аполлона» – он был в скафандре, держал в руке американский флаг и был 3 сантиметра длиной. Я и не знал, что у нее есть такая игрушка. Если вы по спирали скатываетесь в черную дыру, как те бусинки, то будете медленно спускаться в нее либо можете упасть прямо в дыру, как наш аспирант. Я положил игрушечного астронавта на край воронки и просто дал ему соскользнуть вниз – и он исчез в дыре. Отлично. Черная дыра – как тот отель, в который можно заселиться, но покинуть его уже невозможно[33]. Астронавт, падающий прямо в черную дыру, летит по искривленной радиальной линии, устремляющейся в воронку (это геодезическая линия). Когда я отпускаю астронавта, он падает в воронку именно по такой линии – моя модель получается очень точной. Когда к тебе заявляется съемочная группа, съемка растягивается на несколько часов, делается множество дублей, но на государственном телеканале все это сокращается до небольшого сюжета. Телевизионщики засняли все тщательно продемонстрированные примеры с катящимися бусинами, но, как вы думаете, – что попало в эфир? Естественно, игрушечный астронавт, падающий в воронку. Итак, теперь вы знаете, как черная дыра выглядит снаружи: она напоминает воронку с отверстием в углублении.

Решение, найденное Карлом Шварцшильдом в 1916 году, показало, какова форма этой воронки. Но изобретенная Шварцшильдом хитроумная система координат отказывала на радиусе Шварцшильда. Решение демонстрировало, что происходит извне дыры, но не показывало, что же происходит внутри. Ситуация была такова, как будто у нас есть только карта Северного полушария, а ничего к югу от экватора не видно. Считалось, что у черной дыры есть только внешняя сторона. Наконец, в середине 1960-х годов мой коллега Мартин Крускал с факультета прикладной математики Принстонского университета и Дьёрдь Секереш из Университета Нового Южного Уэльса независимо нашли способ расширить эту координатную систему таким образом, чтобы решение описывало и внутреннюю часть черной дыры. Пространственно-временная схема такого решения ныне называется «диаграмма Крускала» (рис. 20.2).

На этой пространственно-временной схеме по горизонтали показано одно пространственное измерение, а по вертикали – время. Будущее находится в верхней части диаграммы. Диаграмма такова, что свет на ней летит по прямым, расположенным под углом 45°. Скорость света постоянна, именно поэтому уклон 45° не изменяется. Давайте проиллюстрируем смысл этих координат, вернувшись к примеру с профессором и его несчастным аспирантом. Для начала проведем черную мировую линию профессора (см. рисунок). Она не прямая, поскольку профессор движется с ускорением: двигатели ракеты постоянно работают, чтобы корабль удерживался на расстоянии 1,25 радиуса Шварцшильда от черной дыры.

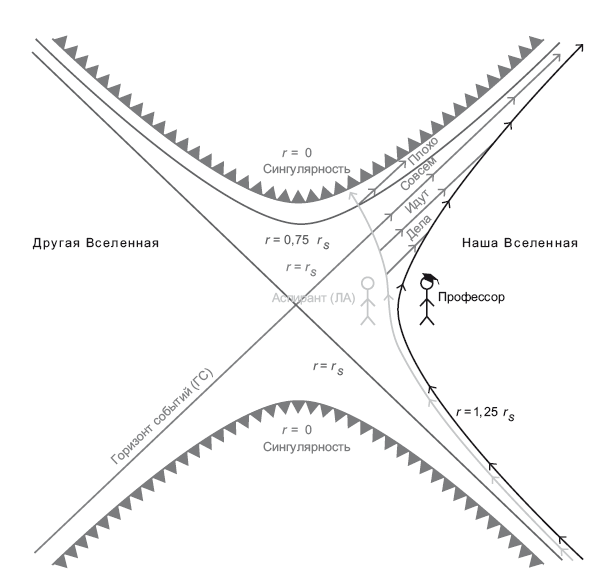
Рис. 20.2. Диаграмма Крускала. Это пространственно-временная схема, демонстрирующая геометрию (невращающейся) черной дыры как в пределах радиуса Шварцшильда, так и вне его. Будущее показано сверху. На схеме изображено искривленное пустое пространство вокруг точечной массы, существовавшей вечно. Наша Вселенная справа. Показаны мировые линии профессора и аспиранта. Профессор остается на безопасном расстоянии от черной дыры (1,25 rS). Аспирант падает в черную дыру и достигает сингулярности в точке r = 0. Горизонт событий (ГС) проходит вдоль линии, где радиус r равен радиусу Шварцшильда (r = rS). Рисунок предоставлен Дж. Ричардом Готтом

Профессор остается за пределами черной дыры. В точке на полпути от верхнего к нижнего краю рисунка мировая линия вертикальна, затем изгибается вправо. В плоском пространстве-времени такая мировая линия могла бы описывать частицу, которая находилась в покое, будучи в центре рисунка, а потом стала двигаться вправо, набирая скорость. Полная мировая линия профессора – это гипербола. Она изгибается, так что в далеком будущем пойдет вверх под углом около 45°, по мере того, как будет стремиться к скорости света. Вспомните принцип эквивалентности: наблюдатель, движущийся с ускорением в плоском пространстве-времени, наблюдает его таким же, каким видит это пространство-время неподвижный наблюдатель (профессор), находящийся в гравитационном поле. Мировая линия профессора на диаграмме Крускала – это гипербола.

Горизонтальная линия, идущая вправо от центральной точки на оси X, где две линии пересекаются под углом 45°, – это мгновенный снимок радиального луча, который поднимается из отверстия на дне воронки прямо вверх в конкретный момент времени (другое измерение воронки, окружное, на диаграмме не показано).

Мировая линия аспиранта (обозначенная ЛА) – зеленая. На первых порах, в нижней части диаграммы, аспирант летит вместе с профессором, и их мировые линии также продолжаются бок о бок, пока аспирант не покидает профессора в центральной (по вертикали) точке мировой линии профессора. Аспирант находится в свободном падении: его мировая линия устремляется в черную дыру, а мировая линия профессора продолжается вправо. Горизонт событий (обозначенный «ГС», там же r = rS – это радиус, равный радиусу Шварцшильда) – это линия, идущая под углом 45°, которая в далеком будущем располагается асимптотически к мировой линии профессора. Она никогда не соприкоснется с мировой линией профессора. Уклон в 45° возникает потому, что луч света (в данном случае – радиоволна) с сигналом «СОВСЕМ» может идти вдоль такой линии. Мировая линия аспиранта пересекает диагональную линию горизонта событий именно в тот момент, когда аспирант посылает сигнал «СОВСЕМ». Профессор так и не получит этот сигнал. Мировая линия профессора на диаграмме соответствует множеству точек, для каждой из которых r = 1,25 радиуса Шварцшильда. Световые (радио) сигналы «ДЕЛА» и «ИДУТ» – это две линии, идущие под углом 45° каждая; сигналы были отправлены еще до того, как аспирант пересек горизонт событий. Два этих сигнала пересекаются с мировой линией профессора. Он получит эти сигналы. Из диаграммы понятно, почему сигнал «ИДУТ» будет лететь до профессора так долго.

Где точки, расположенные на уровне 0,75 радиуса Шварцшильда? Они выстраиваются вдоль гиперболы, напоминающей улыбку, над диагональной линией горизонта событий. Далеко справа она сверху стремится к линии горизонта событий ГС, но так и не соприкасается с ней. Сингулярность в точке r = 0 – еще одна гипербола, напоминающая улыбку, лежащая над линией 0,75 радиуса Шварцшильда. Мировая линия аспиранта стыкуется с этой горизонтальной улыбкой. Мы нарисовали на ней зубы, так что получился оскал челюстей, готовых сожрать аспиранта. Пространство-время настолько искривлено, что сингулярность, которая, как могло бы показаться, должна обозначаться вертикальной линией слева, искривлена, пока не уходит в будущее. На самом деле, стоит аспиранту пересечь горизонт событий – и эта линия оказывается у него в будущем. Теперь она для него так же неизбежна, как наступление следующей среды. Как бы ни пытался он разогнать ракету быстрее скорости света, это невозможно, и аспирант вынужден двигаться вверх под углом 45°. После того как аспирант минует горизонт событий, гипербола, соответствующая сингулярности, нависнет над ним и будет простираться более чем на ±45°, так что его мировая линия неизбежно в нее упрется. Он обречен. Аналогично, сигнал «ПЛОХО», отправленный аспирантом вправо под углом 45° уже после пересечения горизонта событий, также попадет в челюсти сингулярности в точке r = 0.

Можно завершить диаграмму Крускала, чтобы получилось полное решение для точечной массы. Это массивная точка, возникшая в далеком прошлом, которая будет существовать и в бесконечно отдаленном будущем, когда Вселенная совершенно опустеет. Диагональная линия горизонта событий ГС встречается с другой диагональной линией, идущей во встречном направлении. Посреди диаграммы получается огромная фигура X. Этот X делит пространство-время на четыре области. Область, где остался профессор – вне черной дыры, – находится справа от X. Это наша Вселенная. Над X находится внутренняя часть черной дыры, где в будущем (сверху) зияет сингулярность. Под Xрасположена исходная сингулярность, обозначенная r = 0, кажется, что прошлое внизу нахмурилось. Слева находится другая Вселенная, похожая на нашу. Между ней и нашей Вселенной – «кротовая нора», расположенная в середине. Если сделать горизонтальный срез через это пространство-время в самой середине, то получится срез конкретного момента во времени. Геометрически кротовая нора напоминает две воронки, перетекающие друг в друга в самой узкой точке. В дальней правой части воронки видим широкую окружность – это большой радиус, вдали от черной дыры. Влево воронка постепенно сужается, пока не превращается в окружность длиной 2?rS на горизонте событий в центре X. Затем дыра вновь распахивается и достигает большого радиуса, на левой оконечности X. Две воронки стыкуются, образуя кротовую нору. Вдали от дыры воронки постепенно уплощаются и становятся такими же ровными, как баскетбольные площадки, причем они продолжаются до бесконечности. Вообразите себе здание, на втором этаже которого устроена баскетбольная площадка, а в центре площадки просверлена искривленная воронка, ведущая вниз (напоминает лунку на поле для гольфа). Воронка постепенно раскрывается и распахивается так, что на первом этаже (под баскетбольной площадкой) превращается в совершенно ровный потолок. В данном случае баскетбольная площадка – это наша большая Вселенная, а первый этаж – вторая большая Вселенная, сопряженная с нашей через узкую дыру и подобная потолку на первом этаже. Две большие Вселенные соединены кротовой норой в мгновение, обозначенное горизонтальной линией, проведенной через диаграмму. Но через эту кротовую нору невозможно проникнуть из одной Вселенной в другую. Дело в том, что перекладины X расположены ровно под углом 45°. Чтобы перейти из области справа от X (из нашей Вселенной) в область слева от X (в другую Вселенную), нужна мировая линия, отклоненная от вертикали на угол более 45°. То есть нужно двигаться со сверхсветовой скоростью, а это невозможно. Но, в принципе, можно повстречать пришельцев из другой Вселенной внутри черной дыры, в ее верхней четверти (в будущем). Вы могли бы даже пожать друг другу руки. Сказать: «Дружище, мы в беде» – прежде, чем оба погибнете, врезавшись в улыбающуюся сингулярность в будущем. Вы достигнете сингулярности за конечный период времени.

Исходная сингулярность внизу (в прошлом) весьма напоминает сингулярность Большого взрыва, с которой началась наша Вселенная. Эта часть решения называется «белая дыра». Она напоминает черную дыру с обратным ходом времени – как если бы события в черной дыре перематывались назад. Частица может возникнуть в сингулярности белой дыры в нижней части диаграммы, и мировая линия этой частицы попадет в нашу Вселенную. Если частица попадет в черную дыру, то может выйти обратно из белой дыры.

Такие черные дыры, которые мы можем обнаружить, существовали не всегда. Есть реалистичная модель, согласно которой черная дыра может образоваться при коллапсе звезды. Предположим, что на пространственно-временной диаграмме Крускала поверхность коллапсирующей звезды находится прямо под ногами у аспиранта: и когда он еще вместе с профессором, и когда он падает в дыру. Речь о ситуации, когда звезда долгое время сохраняет радиус величиной 1,25 радиуса Шварцшильда, а затем начинает схлопываться в тот самый момент, когда в дыру начинает падать аспирант, – то есть поверхность звезды несется к центру, а вслед за ней падает аспирант. В таком случае мировая линия звезды будет параллельна мировой линии аспиранта и пойдет слева от нее. Под ногами у падающего аспиранта откроются недра звезды, где плотность материи ненулевая и вакуумное решение диаграммы Крускала неприменимо. Просто не обращаем внимания на ту часть диаграммы, что оказалась слева от мировой линии аспиранта, – никакой кротовой норы, никакой другой вселенной, никакой сингулярности внизу, которая напоминала бы белую дыру. Они не образуются, когда черная дыра возникает при коллапсе звезды. Но та часть диаграммы, что лежит справа от мировой линии аспиранта, находится в вакууме, и в этой части все происходящее изображено точно. Аспиранта расплющивает, и его мировая линия утыкается в сингулярность в точке r = 0.

Если бы вы жили внутри звезды (в комнатке с кондиционером), то и вас бы расплющило, когда звезда схлопнулась бы в нулевой объем и приобрела при этом бесконечную плотность. В будущем ваша мировая линия также неизбежно упрется в сингулярность кривизны: вы уткнетесь в r = 0, когда звезда схлопнется до нулевого размера.

Мой вам совет: просто не приближайтесь к радиусу Шварцшильда – и все будет нормально. Можно без проблем вращаться по орбите вокруг горизонта событий черной дыры. Если Солнце сколлапсирует и превратится в черную дыру, то Земля останется вне дыры, на нынешней орбите. Вы увидите черную дыру, которая будет выглядеть как черный диск в небе. Вокруг нее будут искаженные гравитационной линзой звезды, расположенные за дырой (рис. 20.3).

В 1963 году Рой Керр открыл точное решение эйнштейновских уравнений поля для вращающейся черной дыры (такой, что обладает моментом импульса). Такая черная дыра имеет за горизонтом событий более сложную геометрию, которую мы обсудим в главе 21. Но ее горизонт событий – это точка невозврата, точно как и у шварцшильдовской черной дыры. Решение Керра блестяще подтвердилось 14 сентября 2015 года, когда астрономы из лазерно-интерферометрической гравитационно-волновой обсерватории (LIGO) зафиксировали образование вращающейся керровской черной дыры в 62 солнечные массы при столкновении двух черных дыр: одной в 29 солнечных масс, а другой – в 36 солнечных масс. Две эти дыры образовали прочную связку и по спирали устремились друг к другу, теряя энергию в форме гравитационного излучения.

Рис. 20.3. Так могла бы выглядеть шварцшильдовская черная дыра. Она напоминает черный диск в небе, вокруг нее – звезды, контуры которых кажутся искаженными из-за действия гравитационной линзы. Вы видите два изображения Млечного Пути, поскольку свет, попадающий в поле зрения, обходит черную дыру с разных сторон. Иллюстрация предоставлена Andrew Hamilton. Фоновое изображение Млечного Пути обработано на основе иллюстрации Axel Mellinger

Исследуя эту гравитационную рябь в пространстве-времени, астрономы смогли вычислить массы черных дыр, участвовавших в столкновении. Поскольку у двух черных дыр, вращающихся одна вокруг другой, был орбитальный момент импульса, неудивительно, что в центре образовалась вращающаяся черная дыра. Кольцевые колебания этой конечной черной дыры, которая сначала образовалась в движении, а затем успокоилась, в точности соответствовали тем, которые должны возникать при ослабевании пертурбаций керровской черной дыры. Астрономы даже смогли определить, что момент импульса керровской вращающейся черной дыры составил приблизительно 67 % от максимума, возможного для черной дыры с такой массой. Все столкновение, включая образование гравитационных волн, можно смоделировать на суперкомпьютере, решающем эйнштейновские уравнения для вычисления геометрии пространства-времени. Согласованность компьютерной модели и наблюдаемых гравитационных волн показывает, что эйнштейновские уравнения продолжают работать даже в исключительно сильно искривленном пространстве-времени – это очень важный результат.

В 1974 году Стивен Хокинг совершил удивительное открытие, прославившее его: оказывается, черная дыра испускает тепловое излучение. Энергия может вырваться из черной дыры, и действительно вырывается. Как было сделано это открытие? Принстонский аспирант Яаков Бекенштейн беседовал со своим научным руководителем Джоном Арчибальдом Уилером. Уилер был одним из авторов термина «черная дыра». Удачное название! Черные дыры – это дыры, причем черные, ведь они не излучают свет. Как рассказывал Нил, астрономы предпочитают не мудрствовать, именуя объекты: «Оно черное и напоминает дыру – давайте назовем это просто “черная дыра”». Уилер был зачинателем всех исследований, связанных с черными дырами, именно он помог оживить интерес к общей теории относительности в 1960-е годы. Он нашел единомышленников, заинтересованных в работе над этой проблемой, и вместе с Чарльзом Мизнером и Кипом Торном написал классическую книгу, первые редакции которой я штудировал в аспирантуре. Когда Крускал получил свою диаграмму, он отправил ее Уилеру, поинтересовавшись мнением ученого, а сам ушел в отпуск. Уилер прочел статью и нашел ее настолько важной, что подготовил рукопись сам и направил ее в журнал Physical Review, указав, что автор работы – Крускал. Вернувшись из отпуска, Крускал узнал, что статья уже ушла в редакцию.

Уилер пригласил своего аспиранта Бекенштейна поговорить. Взяв чашку горячего чая, Уилер налил в нее немного холодной воды и сказал: «Я только что совершил преступление: повысил энтропию (беспорядок) во Вселенной. И ничего не исправишь: я же не могу вымешать воду обратно из чая». Бекенштейн знал, что энтропия во Вселенной со временем только возрастает. Нечасто увидишь, как осколки самособираются в вазу. На самом деле, когда видишь подобное в кино (эффект достигается обратной перемоткой), становится смешно, поскольку каждый знает, насколько это невероятно. Существует ненулевой шанс, что такое произойдет, но он очень мал. Статистически ожидается, что степень неупорядоченности во Вселенной должна возрастать – этот принцип называется «второй закон термодинамики». Мы любим порядок: стыдно раскокать красивую вазу на черепки. Следуя этой логике, предосудительно любое увеличение энтропии, например подмешивание воды в чай. «Но, – продолжал Уилер, – теперь я могу скрыть улики этого преступления, если брошу остывшую смесь чая и воды в черную дыру. Масса черной дыры при этом увеличивается на массу попавших туда чая и воды. Но она увеличилась бы ровно на столько же, если бы я налил в черную дыру воду и чай отдельно. Итак, восстановлен статус-кво, который существовал бы без смешивания воды и чая, – и, по-видимому, второй закон термодинамики в данном случае нарушается. Подумайте об этом!»

Бекенштейн всерьез воспринял идею Уилера и действительно стал ее обдумывать. Статья, которая получилась у него в результате, кажется мне исключительно важной. Бекенштейн отметил, что Хокинг доказал теорему, согласно которой общая площадь всех горизонтов событий во Вселенной со временем возрастает, если плотность массы повсюду остается неотрицательной, – и это казалось логичным. Когда в черную дыру поступает новая масса, масса черной дыры увеличивается, равно как и ее радиус Шварцшильда. Поверхностная площадь горизонта событий, равная 4?rS², также возрастает. При столкновении двух черных дыр (как в случае, зафиксированном LIGO) возникает новая черная дыра с горизонтом событий, общая площадь которого больше, чем сумма площадей горизонтов событий двух исходных черных дыр. Так, согласно расчетам, проведенным в случае LIGO, площадь горизонта событий получившейся при столкновении вращающейся черной дыры (в 62 солнечные массы) как минимум в 1,5 раза больше, чем сумма площадей горизонтов событий двух исходных черных дыр (в 29 и 36 солнечных масс). С точки зрения Бекенштейна, такой феномен постоянного возрастания площадей горизонтов событий со временем напоминал проявление энтропии, которая, как известно, со временем также лишь возрастает.

Бекенштейн сформулировал мысленный эксперимент: как можно осторожнее (практически чтобы можно было отдернуть) опускаем частицу на струнке в шварцшильдовскую черную дыру и считаем, насколько при этом возросла площадь дыры. Бекенштейн вычислил, что такой акт соответствует потере одного бита информации, а именно информации о том, существовала эта частица или нет. Поскольку потеря информации в контексте данного мысленного эксперимента соответствует минимальному увеличению площади – порядка (1,6 ?10^–33 см)² = hG/2?c³ (все члены формулы нам до боли знакомы: вот постоянная Планка h, вот постоянная Ньютона G, а вот скорость света c). О расстоянии порядка 1,6 ?10^–33 см, именуемом планковской длиной, мы вновь поговорим в главе 24. При таких масштабах геометрия пространства-времени становится нечеткой в силу квантово-механического принципа неопределенности Гейзенберга. Когда Уилер бросал в черную дыру свою чашку с остывшим чаем, он повысил площадь горизонта и энтропию этой дыры. Общая энтропия Вселенной при этом все равно возросла, поскольку увеличилась энтропия черной дыры, как только в нее упала чашка. Бекенштейн заключил, что черные дыры обладают очень большой, но конечной энтропией.

Интересно, что работа Бекенштейна демонстрирует, каков предельный объем информации, которую можно сохранить на 6-дюймовом жестком диске. Это 10⁶⁸ бит = 1,16 ? 10⁵⁸ гигабайт. Если вы попытаетесь записать на жесткий диск такого размера еще больше информации, он станет настолько массивным, что схлопнется в черную дыру (этот случай будет подробно рассмотрен в приложении 2). Кроме того, аргументация Бекенштейна ограничивает и количество информации, которую можно вместить в наблюдаемой части Вселенной и, следовательно, сколько может существовать различных вселенных с такими размерами и такой энергией, как у нашей. Речь о числе 10^(10^124) – Нил упоминал его в главе 1. Итак, статья Бекенштейна нашла разнообразное применение.

Но Хокинг (в отличие от меня) считал, что Бекенштейн ошибается. Если в черную дыру умещается конечный объем энергии и при этом ее энтропия увеличивается на конечную величину, та же самая термодинамическая аргументация предполагает, что у черной дыры должна быть конечная температура. Хокинг был убежден, что здесь кроется ошибка. Черные дыры не светятся, как светился бы объект с конечной температурой. Черные дыры черные – их температура нулевая.

Роджер Пенроуз показал, что в случае вращающейся черной дыры частица может распасться на две другие частицы в области пространства непосредственно снаружи от горизонта событий и одна из частиц может упасть в черную дыру, вращаясь в противоположном направлении относительно вращения черной дыры, и общий момент импульса дыры в таком случае снижался бы, тогда как вторая частица улетела бы от черной дыры с большей энергией, чем была у исходной частицы. Часть массы вращающейся черной дыры приходится на энергию вращения, и постепенно черная дыра вращается все медленнее, так что ее масса становится меньше, чем ранее. Снижение вращательной энергии черной дыры позволяет высвободить ту энергию, которая необходима второй частице, образовавшейся при распаде, чтобы улететь от черной дыры. При этом площадь горизонта событий вращающейся черной дыры немного увеличивается. Димитриос Христодулу, еще один ученик Уилера, исследовал эти вопросы, проверяя, какова предельная энергия, которую можно извлечь из вращающейся черной дыры. Яков Зельдович в СССР применил эту идею при исследовании электромагнитных волн. Он сформулировал эвристический аргумент: электромагнитную волну, пролетающую мимо вращающейся черной дыры, можно усилить, придав ей дополнительную энергию, – как пенроузовской ускользающей частице. Процесс напоминал вынужденное излучение – эффект лазера, открытый Эйнштейном. Если следовать такой логике, то из вращающейся черной дыры также должно литься некое спонтанное излучение: дыра постепенно теряет энергию вращения и испускает электромагнитные волны. Алексей Старобинский рассчитал такие эффекты для волн, расходящихся от вращающейся керровской черной дыры.

По воспоминаниям Дона Пейджа[34], ученика Хокинга, Хокинг хотел подобрать для этих идей более солидное обоснование. Хокинг взялся применить квантовую механику к искривленному пространству-времени, чтобы рассчитать рождение и аннигиляцию частиц в искривленном шварцшильдовском пространстве-времени и проверить, на самом ли деле невращающаяся черная дыра испускает какое-либо излучение. Сам немало удивившись, Хокинг обнаружил, что эти частицы действительно рождаются – от черной дыры исходит тепловое излучение. Оказывается, черная дыра обладает конечной температурой! Хокинг опирался на следующий факт: в вакууме все время рождаются пары частиц, которые сразу же сталкиваются друг с другом и аннигилируют. Это называется «виртуальные пары». Такие частицы всегда возникают и сразу же исчезают. Согласно квантово-механическому принципу неопределенности Гейзенберга, энергия системы характеризуется значительной неопределенностью в течение достаточно кратких промежутков времени. Следовательно, энергию, необходимую для рождения электрона и позитрона (нам понадобятся обе частицы; ведь общий электрический заряд обязательно должен сохраняться), можно ненадолго «позаимствовать» прямо из вакуума. Таким образом, парные частицы электрон и позитрон могут родиться рядом друг с другом из вакуума, затем столкнуться и аннигилировать спустя краткий период (порядка 3?10^–22 секунд). Но в случае с черной дырой электрон может родиться чуть-чуть под горизонтом событий, а позитрон – слегка за пределами горизонта событий. Электрон, рожденный в пределах горизонта событий, не может вырваться оттуда и аннигилировать с позитроном, оставшимся снаружи. Электрон падает в черную дыру, а позитрон улетает. Электрон, родившийся за горизонтом событий, обладает гравитационной потенциальной энергией, которая отрицательна по знаку и больше по величине, чем энергия массы покоя электрона, рассчитываемая по формуле E = mc2. То есть суммарная энергия меньше нуля, и когда такой электрон падает в черную дыру, он крадет у нее часть ее энергии и, следовательно, массы. Это количество идет на образование массы и энергии излученного позитрона. Вокруг черной дыры со слегка отрицательной плотностью энергии существует квантовое состояние вакуума (ныне именуемое вакуум Хартла – Хокинга), нарушающее посылку о положительности энергии, лежащую в основе хокинговской теоремы об увеличении площади. В данном случае, когда позитрон улетает от черной дыры, площадь горизонта событий немного уменьшается. В альтернативном случае в черной дыре может сгинуть позитрон, а электрон при этом улетит. Такой же эффект возможен с парными фотонами, когда один фотон, родившийся под самым горизонтом событий, падает в черную дыру, а другой, родившийся вне его, – улетает. Хокинг обнаружил, что черные дыры испускают тепловое излучение (которое теперь называется излучение Хокинга). В ходе такого процесса черные дыры скукоживаются и в конце концов испаряются. Такое тепловое излучение обладает характерной длиной волны (?_макс) примерно вдвое больше шварцшильдовского радиуса черной дыры. Таким образом, черная дыра в 10 солнечных масс испускает 75-километровые радиоволны – слишком слабые, чтобы их можно было зафиксировать. Температура этого теплового излучения очень низкая – 6 ? 10^–9 К (к нему в минимальном количестве подмешаны электроны и позитроны). Вот почему Стивен Хокинг до сих пор не получил Нобелевскую премию. Если бы это излучение оказалось достаточно сильным, чтобы его можно было зафиксировать уже сегодня, то он наверняка отправился бы в Стокгольм. Думаю, никто не сомневается в существовании этого излучения; но, по прогнозам, оно должно быть чрезвычайно слабым. На самом деле, черные дыры (сравнимые по массе со звездами или более крупные) поглощают больше реликтового излучения (РИ), чем испускают собственного. Лишь в далеком будущем реликтовое излучение достаточно остынет и сместится в красную сторону спектра настолько, чтобы процесс испарения черных дыр набрал ход.

На испарение черной дыры требуется много времени. Черная дыра в 3 ? 10⁹ солнечных масс, подобная той, что находится в центре галактики М87, в настоящее время испускает тепловое излучение с температурой около 2 ? 10^–17 К – в основном в виде фотонов и гравитонов. По расчетам Дона Пейджа, черная дыра в 3 ? 109 солнечных масс должна испариться за 3 ? 10⁹⁵ лет. Сегодня она активнее впитывает реликтовое излучение, чем сама испускает хокинговское. В сущности, черная дыра не начнет терять массу до тех пор, пока температура реликтового излучения не упадет до 2 ? 10^–17 К. Это должно произойти примерно через 700 миллиардов лет. Наконец, в результате долгого испарения черная дыра уменьшится до размера 10^–33 см и исчезнет в виде всплеска исключительно высокоэнергетических гамма-лучей. Считается, что информация, которая теряется при формировании черной дыры, рано или поздно вытекает из черной дыры в виде хокинговского излучения, но в скремблированной (неупорядоченной) форме.

Подробности того, как именно такое испарение сказывается на недрах черной дыры, по-прежнему активно обсуждаются. Некоторые физики считают, что античастицы (или частицы), рождающиеся прямо под горизонтом событий и парные хокинговским частицам (или античастицам), излучаемым с внешней стороны горизонта, могут образовывать файервол – стену из горячих фотонов, расположенную непосредственно перед горизонтом событий, – в ней и сгорит падающий астронавт. Возможно, этот эффект становится существенным лишь после того, как в черной дыре испарится примерно половина массы, – а это произойдет только в отдаленном будущем. Детали зависят от свойств квантового состояния вакуума, возникающего вокруг черной дыры.

Джеймс Хартл и Хокинг обнаружили квантовое состояние, которое не приводило к вспышке на горизонте событий и «пропускало» падающего астронавта в глубины черной дыры. Когда из вакуума рождаются частица и античастица (например, электрон и позитрон), их квантовые состояния запутанны. Две эти частицы обладают взаимно противоположным спином и моментом импульса. Если измерить спин одной из них в конкретном направлении, то сразу же известно, что спин второй в этом же направлении будет противоположен. Эта закономерность сохраняется, даже если частицы находятся очень далеко друг от друга. Данный эффект озадачивал Эйнштейна, он называл его «жутким дальнодействием». Для него это был один из проблемных аспектов квантовой механики. В недавно опубликованной работе Хуан Малдасена и Леонард Сасскинд – двое ведущих современных специалистов в этой сфере – отстаивают мнение, что, благодаря квантовой запутанности между излучаемыми частицами и их партнерами, остающимися за горизонтом событий, астронавт может падать в черную дыру, ничуть не разогреваясь, точно как и предполагали Хартл и Хокинг. Малдасена и Сасскинд считают, что частица и античастица в данном случае соединены крошечной микроскопичской кротовой норой. В принципе, они соприкасаются через кротовину, хотя расстояние в обычном пространстве между ними велико. Кротовая нора напоминает отверстие в столешнице, через которое муравей может переползти с верхней стороны столешницы на нижнюю. Если двигаться по плоскости стола, расстояние между двумя «устьями» норы действительно велико. Муравью пришлось бы ползти и ползти от верхнего до нижнего устья кротовой норы. Сначала ему пришлось бы доползти по столешнице до края стола, затем повернуть и ползти по нижней стороне столешницы, пока, наконец, он не добрался бы до второго устья. Муравей, который бы двигался таким образом, счел бы, что от одного устья до другого долгий путь, а другой муравей, который бы проскочил прямо через кротовину, подумал бы, что два устья расположены довольно близко. Таким образом решается эйнштейновская проблема «жуткого дальнодействия». Частица и античастица всегда близки друг к другу, так как сообщаются через кротовую нору. Интересно, что Уилер уже отмечал: линии электрического поля, сходящиеся у устья кротовой норы, могут выглядеть как электрон (на нижней части столешницы), но, появляясь из верхнего устья, такая частица выглядит уже как позитрон. Следовательно, считал он, частицы и античастицы могут сообщаться через кротовины, например, как в черной дыре, которую мы видели на диаграмме Крускала; эта черная дыра соединяет две Вселенные (и в данном случае называется «мост Эйнштейна – Розена»). Эйнштейн написал статью о жутком дальнодействии в соавторстве с Натаном Розеном и Борисом Подольским. Следовательно, считают Малдасена и Сасскинд, парадокс Эйнштейна – Подольского – Розена о «жутком дальнодействии» разрешим при помощи микроскопического моста Эйнштейна – Розена! Удивительно, что Эйнштейн и Розен (а также кто бы то ни было еще) упустили эту связь! Если эта картина верна, то аспирант, по-видимому, уцелеет при пересечении горизонта событий, как изначально и предполагал Хокинг. Вот пример, демонстрирующий, какие глубокие взаимосвязи вскрыла работа Хокинга.

Помню, как я был воодушевлен, когда Хокинг прибыл к нам в Калтех, чтобы рассказать об открытии: черные дыры могут испаряться. Хокинга представил нам Кип Торн, один из крупнейших в мире специалистов по черным дырам. В аудитории присутствовал нобелевский лауреат Мюррей Гелл-Манн. Торн заверил нас, что по значимости это исследование тянет на революционное. Согласен – это один из важнейших результатов общей теории относительности со времен Эйнштейна. Все вы слышали о Стивене Хокинге, и именно это исследование принесло ему мировую славу. Некоторые из этих захватывающих событий показаны в фильме «Теория всего» (2014 год). Эдди Редмейн получил «Оскар» за то, как убедительно и точно сыграл в этом фильме Хокинга.