Книга: Большое космическое путешествие

Глава 17 Путь Эйнштейна к теории относительности

Глава 17

Путь Эйнштейна к теории относительности

Автор: Дж. Ричард Готт

Фамилия Эйнштейн уже стала синонимом слова «гений». Например, кто-то может сказать: «Эй, Эйнштейн, иди сюда!» («Эй, гений, иди сюда») или «Он не Эйнштейн», то есть «Он не гений». Эйнштейн знаменит своей гениальностью. Ньютон тоже был гением. Но во всем мире и в разные эпохи жили и другие гении. Кто величайшее светило английской литературы? Шекспир! Анализируя его пьесы и стихи, многие утверждают, что у Шекспира был самый богатый в истории подтвержденный словарный запас. В его произведениях насчитывается 31 534 разных слова. Статистический анализ его творчества, выполненный Брэдли Эфроном и Рональдом Тистедом, позволяет предположить, что на самом деле Шекспир знал более 66 000 разных слов. Шекспир победил бы Ньютона в вербальном разделе SAT, а Ньютон, подозреваю, обставил бы Шекспира в математическом разделе SAT. Часто Ньютон оказывается в таких рейтингах выше Эйнштейна, поскольку не только изучал тяготение и оптику, но и сделал важный вклад в математику, изобретя дифференциальное и интегральное исчисление. Но Ньютону еще и повезло родиться в нужном месте в нужное время: в Европе, где обсуждались именно такие задачи. Исаак Барроу, кембриджский профессор, который также стал наставником Ньютона, интересовался вычислением объема бочек и других подобных емкостей – такая задача лучше всего решается именно при помощи интегрального исчисления. Естественно, на тот момент наука уже дозрела до открытия дифференциального и интегрального исчисления. Фактически философ и математик Готфрид Вильгельм Лейбниц был вторым человеком в Европе, который изобрел интегральное и дифференциальное исчисление независимо от Ньютона. Взгляните на карту – Лейбниц был современником Ньютона и жил всего в нескольких сотнях километров от него. Это не просто совпадение – такие идеи в то время обсуждались по всей Европе.

Мир конца XVII века готов был разродиться великими открытиями, ведь Кеплер уже успел количественно выразить наблюдения за положениями планет, изложенные Тихо Браге на 600 страницах, и сформулировал на их основе три простых закона движения планет, причем эти законы подчинялись математическому анализу. Как рассказывал Майкл в главе 3, Ньютон воспользовался третьим законом Кеплера для расчета силы тяготения, 1/r². Аналогичная ситуация возникла и в XX веке: экспериментальные данные о длине волны водорода в серии Бальмера вывели ученых на формулу, описывающую энергетические уровни в атоме водорода и подготовили почву для квантовой трактовки атома, предложенной Нильсом Бором и Эрвином Шрёдингером.

Журнал Time назвал Эйнштейна наиболее влиятельным человеком XX века. В других веках такого звания по версии Time удостоились Гутенберг, королева Елизавета I, Джефферсон и Эдисон. Шекспир в список не попал, поскольку в XVII веке Time выделил Исаака Ньютона.

В Тринити-колледже Кембриджского университета установлена очень красивая статуя Ньютона в полный рост. Уильям Вордсворт написал о ней стихи, где есть строки:

На постаменте надпись: «Newton Qui genus humanum ingenio superavit», что переводится как «Ньютон, кто превзошел своим умом весь род человеческий». Для тех, кто подобно Нилу считает Ньютона умнейшим человеком в мире, эта фраза послужит реальным аргументом, увековеченным в мраморе. Статуя Эйнштейна гораздо выше человеческого роста установлена в Вашингтоне, столице США, неподалеку от Мемориала ветеранов войны во Вьетнаме и перед фасадом Национальной академии наук. Этот монумент изображает сидящего Эйнштейна, и все равно его высота больше 3,5 м. Дети приходят и играют у колен Эйнштейна.

Теперь давайте немного подробнее сравним Эйнштейна и Ньютона. Я не собираюсь оспаривать мнение Нила о том, что Ньютон – величайший ученый всех времен. Хочу воздать Ньютону должное. Но я собираюсь доказать, что Эйнштейн мог бы посоперничать за это звание и был человеком того же калибра, что и Ньютон.

Каково самое знаменитое уравнение Ньютона?

А самое знаменитое уравнение Эйнштейна?

Какая из двух этих формул более известна? Ньютоновское уравнение, подробно рассмотренное в главе 3, означает, что чем массивнее объект, тем тяжелее он набирает скорость. Формула важна с точки зрения динамики, но довольно проста. На фортепиано сложнее играть, чем на гармошке. Уравнение Эйнштейна означает, что крохотную массу можно преобразовать в огромную энергию. Этот секрет – суть атомного взрыва. Он позволяет понять, как светит Солнце. Какое уравнение кажется вам более важным?

У Ньютона есть еще одно знаменитое уравнение, F = GmM/r², характеризующее гравитационное взаимодействие между двумя материальными точками с массами m и M. Оно довольно важное. У Эйнштейна также есть другое уравнение: E = h?, означающее, что свет состоит из порций энергии, именуемых фотонами, и энергия фотона равна произведению постоянной Планка h на частоту фотона ?.Следует признать: Ньютон считал, что свет состоит из частиц, однако Эйнштейн это доказал. Свет обладает как корпускулярными, так и волновыми свойствами, и такой дуализм критически важен для квантовой механики.

Оба наших героя изобретали. Ньютон сконструировал телескоп-рефлектор. Все крупные телескопы современности – рефлекторы. Космический телескоп «Хаббл» и телескопы обсерватории Кека – рефлекторы. Эйнштейн разработал принципы, на основе которых работает лазер. Всякий раз, когда вы слушаете CD или смотрите DVD, вы пользуетесь изобретением Эйнштейна. Оба наших героя отметились на государственной службе. Ньютон заведовал Королевским монетным двором. Он изобрел насечки на гурте монеты, с тех пор края у монет ребристые. С такими насечками воры уже не могли спиливать края серебряных монет и пускать эти монеты в оборот по номиналу. Если насечки спилены, это сразу видно. Всякий раз, держа в руках монетку, можно пощупать изобретение Ньютона. Ключевое вмешательство Эйнштейна в мировую политику также известно: он написал президенту Франклину Рузвельту историческое письмо, благодаря которому был запущен Манхэттенский проект и созданы атомные бомбы. Тот поступок Эйнштейна был настолько важен, что эффект его ощущается и сегодня.

Эйнштейн был настолько известной персоной, что о нем даже любили рассказывать анекдоты, которые затем вошли в «эйнштейниану». Вот одна из таких шуток (возможно, не строго историческая). Как-то раз Эйнштейн говорил с одним человеком в Принстонском институте перспективных исследований. Вдруг собеседник вытащил из кармана пальто блокнотик и что-то в нем записал. «Что это»? – спросил Эйнштейн. «А, блокнот, – ответил человек, – всегда ношу с собой, так что если на ум придет хорошая идея – записываю, чтобы не забыть». – «Я легко обхожусь без такого блокнота, – ответил Эйнштейн, – у меня было всего три хорошие идеи». Итак, что же это были за идеи и как Эйнштейн до них додумался?

Первая – это специальная теория относительности, благодаря которой появилась формула E = mc². Вторая – это идея о фотоэлектрическом эффекте, заложенная в формуле E = h?; именно за это открытие Эйнштейн получил в 1921 году Нобелевскую премию по физике. Третья – общая теория относительности, при помощи которой Эйнштейн объяснил гравитацию как свойство искривленного пространства-времени. Проработав уравнения этой теории, Эйнштейн спрогнозировал, что свет должен искривляться, проходя в пространстве-времени поблизости от Солнца, а также рассчитал, какова должна быть такая кривизна. Звезды, расположенные вблизи от солнечного диска во время солнечного затмения, должны казаться немного смещенными в небе по сравнению со снимками тех же звезд, сделанных несколькими месяцами ранее, когда Солнце находилось совсем в другой части неба. Величина искривления, спрогнозированная Эйнштейном (1,75 секунды дуги близ лимба, края солнечного диска), была вдвое больше аналогичной величины, которую Ньютон, согласно собственной теории, мог бы дать для частиц, летящих со скоростью света. Сэр Артур Эддингтон возглавил экспедицию, специально снаряженную для того, чтобы измерить этот эффект. Оказалось, что прогноз Эйнштейна верен, а прогноз Ньютона ошибочен. Сегодня мы оперируем теорией Эйнштейна, а не теорией Ньютона. Давайте сделаем паузу и оценим это!

В самом конце XX века я видел по телевизору программу о величайших спортивных достижениях уходящего столетия: Джесси Оуэнс – чемпион стометровки на олимпиаде 1936 года в Берлине; жеребец Секретариат выигрывает забег «Белмонт Стэйкс», обойдя ближайшего конкурента на 31 корпус, и завоевывает «Тройную Корону»[24]; Мохаммед Али нокаутирует Джорджа Формана в Заире и возвращает себе титул чемпиона мира по боксу в тяжелом весе. А каков был величайший эпизод в истории науки XX века? Представьте себе: Ньютон и Эйнштейн соревнуются на баскетбольной площадке.

Ньютон завладел мячом. Ведет дриблинг. И это не просто мяч, а его теория тяготения – самое пафосное достижение, которое он сделал в жизни! Тут Эйнштейн догоняет его, отбирает мяч, бросок, и – вжух! – мяч в корзине. Это величайшая игра в науке XX века.

Хочу объяснить, как Эйнштейн нащупал свои великие идеи. Он хорошо учился в школе. Имел высокие баллы по естественным наукам. Возможно, вы слышали истории о плохой успеваемости Эйнштейна – забудьте их. Эйнштейн познакомился с наукой в четыре года, когда отец показал ему компас. Он весьма увлекся этой игрушкой, и с нее начался путь Эйнштейна в науку. Эйнштейн самостоятельно освоил интегральное и дифференциальное исчисление, будучи примерно в двенадцатилетнем возрасте. Умный малый. А когда ему было 16, Эйнштейн стал размышлять о самой захватывающей физической теории своего времени – максвелловской теории электромагнетизма. Максвелл объединил все разнообразные законы электричества и магнетизма.

Электрические заряды могут быть или положительными, или отрицательными. Противоположные заряды притягиваются, а одинаковые отталкиваются с силой, пропорциональной 1/r². Два положительных заряда отталкиваются, и два отрицательных тоже отталкиваются, а положительный и отрицательный – притягиваются. Это закон Кулона. Именно он – причина статического электричества. Заряды генерируют электрические поля, заполняющие пространство между ними, причем если вы – заряд, то электрическое поле придает вам ускорение. Электрическое поле сообщает вам силу, пропорциональную 1/r². Именно поэтому одежда зимой накапливает статическое электричество, из-за которого к чему-нибудь прилипает. Но движение зарядов вдобавок порождает магнитное поле, а если вы – движущийся заряд, то это магнитное поле может на вас воздействовать. Если заряд не движется, то приложенная к нему магнитная сила равна нулю, но если он движется в магнитных полях, то на этот заряд будет действовать некоторая магнитная сила. Эти идеи выражены в виде еще нескольких физических законов: закон Ампера сообщает, как движущиеся заряды (например, ток в проводе) генерируют магнитное поле, и вы, зная значения магнитного и электрического полей в некоторой точке, можете вычислить, каковы электрические и магнитные силы, воздействующие на движущийся заряд в данной точке. Закон Фарадея описывает, как изменяющееся магнитное поле порождает электрическое поле. Причем давно известно, что «магнитных зарядов» не бывает; то есть вы нигде не найдете отдельный северный (или отдельный южный) магнитный полюс, от которого распространяется магнитное поле. По закону сохранения заряда общее количество зарядов (число положительных минус число отрицательных) остается постоянным. Например, если в некоторой области 10 положительных зарядов и 9 отрицательных, то общий заряд этой области равен +1. Положительные и отрицательные заряды могут притягиваться, компенсируя друг друга, например, может остаться 9 положительных зарядов и 8 отрицательных, но общий заряд останется равным +1.

Максвелл изучил известные в его время законы электромагнетизма и заключил, что они противоречат закону сохранения заряда. Чтобы исправить это, он показал, что необходимо учесть еще один эффект: изменяющееся электрическое поле порождает магнитное поле. Все эти эффекты он выразил в виде четырех уравнений, которые называются уравнениями Максвелла (иногда студенты-физики даже носят футболки с этими уравнениями!).

В уравнениях Максвелла есть постоянная c, характеризующая соотношение сил электрических и магнитных зарядов. Если у нас есть сгусток зарядов, движущийся со скоростью v, то соотношение порождаемых ими электрических и магнитных сил будет пропорционально v²/c², где с – некоторая скорость. Затем он принялся ставить лабораторные эксперименты, сравнивая электрические и магнитные силы и стараясь вычислить, чему равна постоянная c. У него получилось очень высокое значение: эта константа равнялась примерно 310 740 км/c. Максвелл также нашел исключительно интересное решение собственных уравнений: им удовлетворяла электромагнитная волна, распространяющаяся в вакууме со скоростью c.

Магнитные и электрические поля располагались перпендикулярно вектору скорости волны. Волна имела форму синусоиды, и электрические и магнитные поля колебались по синусоиде в некоторой точке, через которую проходила эта волна. Следовательно, изменялось и электрическое, и магнитное поле. Изменяющееся электрическое поле порождало магнитное, а изменяющееся магнитное поле порождало электрическое, и они так и тащили друг друга вдоль волны, распространяясь в вакууме со скоростью c = 310 740 км/c.

Эврика! Максвелл понял, что скорость с – это скорость света. Должно быть, свет – это электромагнитные волны! Это был один из научных триумфов. Откуда Максвелл знал скорость света? Помогли астрономы – здесь я хочу выступить от имени астрономов, – уже измерявшие скорость света! В 1676 году датский астроном Оле Рёмер заметил, что последовательные затмения Ио, спутника Юпитера, случались чаще, когда Земля приближалась к Юпитеру, и реже, когда Земля удалялась от Юпитера. Спутники Юпитера, за которыми наблюдал Рёмер, напомнили ему гигантский циферблат. Когда мы приближаемся к Юпитеру, эти часы спешат, а когда удаляемся от него, они запаздывают. Рёмер сделал верный вывод: это происходит, поскольку скорость света конечна. Когда мы приближаемся к Юпитеру, расстояние до него уменьшается, свет, отражающийся при последовательных затмениях, достигает нас быстрее. Этот эффект напоминает доплеровское смещение от множества затмений, рассматриваемых как одно целое. Рёмер вычислил, что свет должен преодолевать радиус земной орбиты приблизительно за 11 минут. На самом деле для этого требуется примерно 8 минут, так что оценка Рёмера получилась довольно точной. Когда Земля и Юпитер максимально сближаются, «часы» Юпитера спешат примерно на 8 минут, а когда две планеты дальше всего друг от друга, эти часы запаздывают на 8 минут. В главе 8 мы уже обсуждали, как Джованни Кассини в 1672 году измерил расстояние до Марса по его параллаксу и таким образом смог определить радиус земной орбиты. Воспользовавшись данными Рёмера и примерно зная радиус земной орбиты, Христиан Гюйгенс смог вычислить скорость света: у него получилось 220 000 км/с (что всего на 27 % ниже истинного значения 299 792 км/c).

В 1728 году другой астроном, Джеймс Брэдли, измерил скорость света иным способом. Представьте себе звезду прямо над головой. Ее свет падает прямо на вас, словно дождь. Когда едешь на машине, дождь льется по стеклам под углом, поскольку вы движетесь. Земля летит по околосолнечной орбите со скоростью 30 км/c и похожа на движущуюся машину. Если направить телескоп прямо вверх, то свет будет падать на него и попадать в окуляр под наклоном, ведь мы движемся. Чтобы рассмотреть звезду, телескоп нужно наклонить, чтобы он находился под таким же углом, что и «дождь», льющийся на «машину», то есть на Землю. Насколько? Телескоп нужно наклонить примерно на 20 секунд дуги. Наблюдая ту же звезду спустя 6 месяцев, вы должны будете отклонить телескоп на 20 секунд дуги в другую сторону. Брэдли удалось измерить такой эффект, который называется «звездная аберрация». Степень такого уклона равна v_ЗЕМЛ/v_СВЕТ, Брэдли в данном случае получил результат примерно 1 часть на 10 000. Таким образом, он сделал вывод, что скорость света примерно в 10 000 раз выше скорости орбитального движения Земли (30 км/c) и, следовательно, равна 300 000 км/c. Поэтому Максвелл в 1865 году, спрогнозировав, что электромагнитные волны должны распространяться в вакууме со скоростью около 310 740 км/c, тогда же понял, что это и есть скорость света, уже измеренная астрономами (300 000 км/c). Два этих числа вполне соответствовали друг другу с поправкой на понятную погрешность его прогноза (связанную с ошибками при измерении электрических и магнитных сил), а также на ошибки при астрономических наблюдениях. Оказалось, что свет – это электромагнитные волны. Максвелл понял, что длина разных электромагнитных волн может быть гораздо короче или длиннее, чем волн видимого света. Короткие электромагнитные волны сегодня известны под названием «ультрафиолетовые лучи», «рентгеновские лучи» или «гамма-лучи», а сравнительно длинные называются «инфракрасные лучи», «микроволны» и «радиоволны». В 1886 году Генрих Герц доказал существование электромагнитных волн, передавая радиоволны по комнате и принимая их там же. Во времена Эйнштейна теория Максвелла была самой захватывающей научной теорией, и Эйнштейн также проявлял к ней самый живой интерес.

В 1896 году, когда Эйнштейну было всего 17 лет, он вообразил следующий мысленный эксперимент. Допустим, ровно в полдень мы начали удаляться от башенных курантов со скоростью света. Если мы обернемся и посмотрим на них, то стрелки как будто застынут на отметке «полдень», поскольку свет, отразившийся от них в этот момент, будет лететь с той же скоростью, что и мы. Останавливается ли время, когда летишь со скоростью света? Эйнштейн задумался, как будет при этом выглядеть луч света, летящий рядом. В таком случае он увидел бы неподвижные волны электрических и магнитных полей, напоминающие борозды на обычном поле; они не будут двигаться относительно наблюдателя. Если лететь с той же скоростью, что и волна, то волна покажется неподвижной. Но такая стационарная волноподобная конфигурация электрических и магнитных полей в вакууме не допускалась максвелловскими уравнениями поля. Картина, которую мы бы увидели из иллюминатора воображаемой фотонной ракеты, казалась невозможной. Эйнштейн понял, что ситуация парадоксальна, а значит, он где-то ошибается. Ему потребовалось девять лет, чтобы догадаться, как исправить эту ошибку.

Эйнштейн действовал очень оригинально. В 1905 году он решил принять два постулата.

1. Движение относительно. Эффекты физических законов должны выглядеть одинаково для любого наблюдателя, находящегося в равномерном движении (это движение с постоянной скоростью в одном и том же направлении, без поворотов).

2. Скорость света в вакууме постоянна. Скорость света c должна получаться одинаковой, если ее измерит любой наблюдатель, находящийся в равномерном движении.

Два этих постулата лежат в основе специальной теории относительности Эйнштейна. Она называется теорией относительности, поскольку «движение относительно» (первый постулат), и специальной – потому что касается только равномерного движения. Первый постулат вы испытываете на себе. Доводилось ли вам летать на пассажирском самолете со скоростью 800 км/ч (по прямой, без поворотов), когда шторки в салоне опущены и можно посмотреть какой-нибудь плохой фильм? Вам кажется, что вы сидите, как будто и не взлетали. В летящем самолете вы находитесь словно в состоянии покоя. Прямо сейчас мы летим вокруг Солнца со скоростью 30 км/c, но нам кажется, что мы никуда не движемся. Первый постулат теории относительности: важны лишь относительные движения, и абсолютный эталон неподвижности определить невозможно. Закон тяготения Ньютона соответствует этому постулату. Согласно этому закону, ускорение (изменение скорости) двух материальных точек зависит от расстояния между ними и никак не связано со скоростями самих этих частиц. Следовательно, Солнечная система была бы устроена одинаково, если бы Солнце оказалось неподвижным, вокруг него вращались бы планеты, либо если бы все это хозяйство летело как одно целое на скорости 100 000 км/c. C точки зрения Ньютона оба случая равноценны. Невозможно поставить в Солнечной системе такой гравитационный эксперимент, который бы показал, движется эта система или нет. На самом деле она движется, вращается вокруг центра Галактики со скоростью около 220 км/c. Теория Ньютона подчиняется первому постулату, и Эйнштейн считал, что уравнения Максвелла также должны ему подчиняться. Все законы физики должны подчиняться этому постулату.

Второй постулат непростой. Он означает, что если я измерю скорость пролетающего мимо меня луча света, то она должна составить 300 000 км/c. Но если кто-то другой пронесется мимо меня на скорости 100 000 км/c и измерит скорость того же луча света, она также должна составить 300 000 км/c, а не 200 000 км/c, как мы могли бы предположить. Он должен увидеть луч света, летящий со скоростью 300 000 км/c, то есть с такой же скоростью, которую измерил бы я. Это безумие!

Да, здравый смысл здесь отсутствует. Скорости должны складываться. На самом деле, парадокс обретает смысл, только если часы у второго наблюдателя идут с иной скоростью, нежели у меня, и измеренные нами расстояния также отличаются. Примечательно, что Эйнштейн просто поверил в два этих постулата, а здравый смысл отбросил за ненадобностью. В шахматной партии мы бы назвали подобный шаг «отличный ход» (обозначается!!) – подобный ход может обеспечить мат сопернику спустя 17 ходов. Эйнштейн предположил, что два его постулата верны, решил доказать теоремы на основе мысленных экспериментов, выводимых из этих постулатов, и посмотреть, что получится. Если потом сверить эти теоремы с наблюдениями – и наблюдения их подтвердят, то, значит, и сами постулаты верны. Это было поразительно. Никто и никогда ранее не делал ничего подобного. Постулаты Эйнштейна поддавались опровержению[25]. Если бы эйнштейновские теоремы привели его к выводам, которые противоречили бы наблюдениям, то теория тем самым была бы опровергнута. Если бы теоремы согласовывались с наблюдениями, то самих постулатов мы, конечно бы, при этом не доказали, но нашли бы факты в их пользу.

Почему Эйнштейн поверил во второй постулат? Потому, что скорость света в уравнениях Максвелла являлась постоянной и была связана с соотношением магнитных и электрических сил, которые можно измерить в лаборатории. Максвелл вычислил, что волны света распространяются в вакууме со скоростью около 300 000 км/c. Если бы вы зафиксировали луч света, летящий с другой скоростью – например, 200 000 км/c, – то могли бы логически заключить, что движетесь со скоростью 100 000 км/c, вообще понять, что движетесь. Это противоречило бы первому постулату. В 1887 году Альберт Майкельсон и Эдвард Морли поставили знаменитый эксперимент, при котором пытались измерить скорость Земли, вращающейся вокруг Солнца, по отражению солнечных лучей от установленных в лаборатории зеркал. Фактически они измеряли разницу скоростей света относительно своей лаборатории для лучей, летящих параллельно и перпендикулярно вектору скорости Земли. Они добились достаточной чувствительности эксперимента для измерений на скорости 30 км/c, с которой Земля движется вокруг Солнца. Удивительно, но скорость Земли у них получилась нулевой, как если бы Земля была неподвижной, а лучи света относительно их лаборатории летели бы во всех направлениях с одинаковой скоростью. Но именно такой результат они и должны были получить в соответствии со вторым постулатом Эйнштейна. Измеренная вами скорость света всегда будет одинакова, независимо от того, движется Земля или нет. Следовательно, если вы верите во второй постулат, то могли бы спрогнозировать, что Майкельсон и Морли зафиксируют в своем эксперименте нулевую скорость.

Итак, Эйнштейн решил поверить в два своих постулата и доказывать теоремы, исходя из них. Вот один из его выводов: нельзя сконструировать ракету, развивающую сверхсветовую скорость. Почему так? Допустим, я направляю лазерный луч на стену комнаты; он достигает стены. Я могу полагать, что нахожусь в состоянии покоя. Но если сконструировать ракету, развивающую сверхсветовую скорость, и повторить у нее на борту тот же эксперимент, то результат будет иным. Если вы находитесь в центре ракеты и направляете лазер в ее носовую часть, то свет туда никогда не долетит. Любой спортсмен вам скажет, что нельзя догнать соперника, который бегает быстрее вас и опережал вас на старте. Лазерный луч никогда не долетит до носовой части ракеты, так как носовая часть летит быстрее него (быстрее света) и стартовала раньше. Естественно, если бы вы поставили такой эксперимент в корпусе ракеты, то лазер никогда не достиг бы ее носовой части, и вы бы знали, что движетесь (на самом деле быстрее света). Но подождите – это противоречит первому постулату. Поскольку вы летите с постоянной скоростью в одном и том же направлении, вы никак не можете доказать, что движетесь. Ваш эксперимент должен дать тот же результат, что и эксперимент у меня в комнате. Следовательно, невозможно сконструировать ракету, развивающую сверхсветовую скорость. Странный результат, но с ним придется согласиться, если вы согласны с двумя постулатами. Если ракета летит медленнее скорости света, то лазерный луч рано или поздно попадет в ее носовую часть. На это может уйти немало времени, но, например, если ваши часы идут достаточно медленно, то все получится. Летать со субсветовой скоростью можно, но нельзя сконструировать ракету, развивающую сверхсветовую скорость. Этот тезис был проверен на ускорителях частиц, где протоны и электроны разгоняют все сильнее и сильнее, они развивают скорости все ближе и ближе к световой, но скорости света так и не достигают.

Вот другой результат. Вообразите себе «светочасы», устройство, в котором луч света отражается по вертикали между двумя зеркалами, одно из которых расположено, скажем, на потолке, а второе на полу. Каждое отражение – это такт часов. Скорость света равна 300 000 километров в секунду или примерно 30 см в наносекунду. Одна наносекунда – это миллиардная часть секунды. Если расположить два зеркала на расстоянии всего 90 см, то часы будут тикать с частотой раз в 3 наносекунды (рис. 17.1).

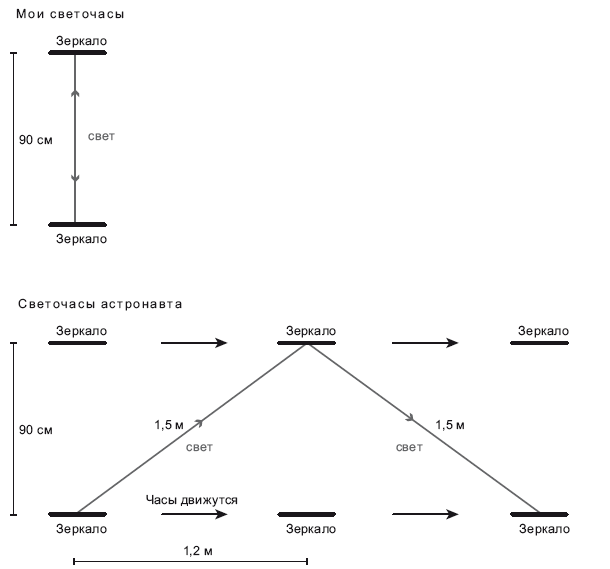
Рис. 17.1. Светочасы. Мои светочасы тикают каждые 3 наносекунды. Аналогичные светочасы взял с собой астронавт, корабль которого летит относительно меня со скоростью 80 % от световой. Свет движется с постоянной скоростью: 30 сантиметров в наносекунду. Я вижу, как лучи света от часов астронавта летят по длинным полутораметровым диагональным отрезкам и, следовательно, мне кажется, что светочасы астронавта тикают каждые 5 наносекунд. Иллюстрация предоставлена Дж. Ричардом Готтом, адаптирована из Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

Это очень быстрые часы. По конструкции похожи на стоячие часы с маятником, только очень быстрые. Свет будет отражаться между двумя зеркалами туда-сюда, туда-сюда. На моих светочасах он будет попадать в зеркало каждые 3 наносекунды. А теперь представьте себе астронавта, летящего на ракете со скоростью 80 % от световой и взявшего с собой аналогичные светочасы (рис. 17.1). Он летит медленнее скорости света, так что опыт сработает. С точки зрения астронавта, его часы тикают нормально, свет преодолевает путь от зеркала до зеркала за 3 наносекунды. Но если я загляну в иллюминатор его ракеты, то увижу, что его часы летят вместе с ракетой на скорости 80 % от световой, а луч света в них летит по диагональной траектории. Луч света летит снизу, но к тому времени, как он преодолеет 90 см, верхнее зеркало уже успеет сдвинуться вправо на 120 см. Свет летит по диагональной траектории, состоящей из отрезков по 150 см. Получается прямоугольный треугольник со сторонами 3–4–5: 90 см по вертикали, 120 см слева направо и гипотенуза длиной 150 см. Треугольник удовлетворяет теореме Пифагора: 3² + 4² = 5². Тогда как относительно меня свет проходит 150 см по диагонали из левой нижней точки в правую верхнюю, с точки зрения астронавта свет преодолевает 120 см слева направо. Следовательно, астронавт движется относительно меня с 4/5, или 80 %, скорости света. Поскольку мне должно казаться (согласно второму постулату), что луч света преодолевает 30 см в наносекунду, я должен сказать, что свет успевает пройти отрезок диагональной траектории длиной 150 см, из нижней точки слева в верхнюю точку справа. Именно это я и наблюдаю. Еще через 5 наносекунд он вновь опустится по диагонали и попадет в нижнее зеркало на 240 см правее, нежели в начале предыдущего отскока. Соответственно я должен сказать, что часы астронавта тикают с частотой раз в 5 наносекунд, а не раз в 3 наносекунды. Мне кажется, что его часы идут медленнее моих со скоростью 3/5 по отношению к ним.

Теперь переходим к самому интересному. Мне должно казаться, что и сердце у астронавта бьется медленнее, чем у меня (также со скоростью 3/5 от моего), либо он сам сравнит ход светочасов со своим пульсом и заметит, что они идут медленнее, и таким образом сможет логически догадаться, что движется (а это противоречит первому постулату). Любые часы, имеющиеся у него на борту, также должны замедляться, идти со скоростью 3/5 от обычной, либо он сможет понять, что движется. Если у астронавта будет мюон (это нестабильная элементарная частица тяжелее электрона), который непременно распадается, то на борту ракеты он должен распадаться медленнее. Астронавт медленнее съедает обед. Еще… он… медленнее… разговаривает. Все процессы на борту ракеты идут медленнее.

Степень замедления зависит от того, с какой скоростью движется астронавт. Если я успею состариться на 10 лет, то (согласно аналогичным расчетам с использованием светочасов[26]) астронавт за это время состарится на 10 лет умножить на ?1 – (v²/c²)[27]. Если говорить о скоростях, которые слишком малы по сравнению со световой – например, скорости, с которыми мы имеем дело в повседневной жизни, – то такой коэффициент старения будет практически равен 1. Если отношение v/c невелико по сравнению с 1, то величина (v²/c²) будет совершенно крошечной по сравнению с 1; если вычесть такой мизер из 1, то останется число, практически равное 1, а квадратный корень из 1 равен 1 – таким образом, этот коэффициент существенным образом не скажется на старении астронавта. То есть астронавт состарится на те же 10 лет, что и я, и разница в возрасте у нас будет незаметна. Вот почему мы обычно не замечаем, что движущиеся часы тикают медленнее неподвижных. Но если астронавт движется на субсветовой скорости, допустим, на 99,995 % скорости света, – то v/c = 0,99995 и ?1 – (v²/c²) = всего 0,01. Можете проверить на калькуляторе. То есть за 10 лет я старею на 10 лет, а астронавт – всего на 1/10 года. При субсветовых скоростях замедление времени на космическом корабле может быть весьма впечатляющим.

Мы верим в эту формулу, так как она проверена экспериментально. Физики брали атомные часы на борт самолета и летели на восток, так что скорость самолета складывалась со скоростью вращения Земли. Оказалось, что эти атомные часы действительно отстали (примерно на 59 наносекунд) по сравнению с атомными часами, оставшимися в аэропорту. Период полураспада мюона в лабораторных условиях равен 2,2 микросекунды, то есть половина мюонов распадается за 2,2 микросекунды. Но мюоны (в виде космических лучей) подлетают к Земле почти на скорости света и распадаются гораздо медленнее (в соответствии с формулой Эйнштейна). Мы верим в правильность этой формулы, поскольку она многократно проверена. Мы живем в забавной Вселенной, работающей по странным законам, но, по-видимому, именно в такой Вселенной мы и живем. Кажется, два постулата Эйнштейна верны. В следующей главе мы рассмотрим, как из двух этих постулатов следует вывод, что E = mc²(эта формула подтвердилась при взрыве атомной бомбы). Такие результаты поистине замечательны. Замечательны потому, что и сами постулаты выдающиеся. Чем больше мы проверяем эти выводы, тем больше убеждаемся в справедливости постулатов.