Книга: Прикладные аспекты аварийных выбросов в атмосферу

3.2. Параметры расширения струй и клубов

3.2. Параметры расширения струй и клубов

Как отмечалось выше, для описания процессов, происходящих в свободных турбулентных течениях, основным понятием является механизм диффузии или «вовлечения» окружающей жидкой или газообразной среды в выброс; граница потока деформируется крупномасштабными вихрями, а внутри — вихри мелкомасштабные широкого спектра размеров.

Процесс перемешивания внутреннего и внешнего течений происходит в два этапа: захват внешней среды большими вихрями и каскадное мелкомасштабное перемешивание в ядре потока.

Детальная теория механизма вовлечения дается в основополагающей работе Таунсенда [154], но упрощенно описанный выше механизм этого процесса дает представление о физике явления.

Для нахождения параметров расширения струйного потока будем исходить из геометрической интерпретации процесса нарастания его поперечного размера. Все работы, использующие понятие вовлечения, базируются на интегральном (осредненном по поверхности контакта с окружающей средой по периметру контрольного элемента газа) поступлении вещества окружающей среды в турбулентный поток. Считается [5 — 14], что приток воздуха на внешней периферии контрольного элемента газа единичной длины (Рис. 3.1) равен вовлечению Е в струю, то есть

Е = ?_е · L · w. (3.1)

где

L — длина внешней образующей поперечного сечения S (для круглого сечения L = 2?R); w — скорость вовлечения внешнего воздуха в сечение S (среднее по длине ?l).

Считается, что скорость вовлечения пропорциональна скорости вещества струи V, т. е.

w = а V

где а — коэффициент вовлечения.

В большинстве работ коэффициент а считается постоянным, однако в действительности это не так. Только в одном частном случае осесимметричной изотермической струи при отсутствии сносящего потока, как показывает опыт [11] это соотношение постоянно.

Соотношение w/V характеризует угол раствора струйного потока. Естественно, что оно должно зависеть от плотностей вещества струи и окружающей среды и от их степеней турбулентности. Рику и Сполдинг [96] экспериментально получили зависимость коэффициента вовлечения от плотности. Ими было получено соотношение

w / V = ?,

где ? = а (?/ ?_е) S.

По данным [12,13] а = 0,08 для осесимметричной струи и а = 0,22 — для струи линейной [14] при экспериментах в лабораторных условиях, что соответствует случаю покоящейся среды (штиль). В такой постановке в настоящее время решаются наиболее «продвинутые» задачи теории струй.

Выражение (3.1) при этом приобретает следующий вид:

где 

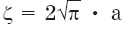
Вовлечение Е в форме (3.2) при записанных выше постоянных значениях коэффициента а уже учитывает неоднородность плотностей окружающей среды и струи и очевидно вполне приемлемо для лабораторных практически штилевых условий, но оно не зависит от динамических и метеорологических характеристик атмосферного воздуха, которые существенно влияют на турбулентный захват струей внешней среды, и поэтому не пригодно для описания процессов в реальной атмосфере. Зависимость вовлечения при такой записи от динамической активности внешней среды отсутствует и поэтому «одна из основных задач теории турбулентности» (как отмечается в [11]) пока остается не решенной до конца. Для ее решения следует положить С, переменным — связанным интегрально с пульсационными параметрами атмосферы.

Сохраним форму записи (3.2), предполагая однако, что С, (или а) не константа, а некоторый параметр, зависящий от степени турбулентности атмосферы или иначе от ее устойчивости. По классификации Пасквилла [15,50] атмосфера по характеру устойчивости может быть подразделена на 7 градаций или классов (А, В, С, D, Е, F, G), причем каждому классу можно поставить в однозначное соответствие угол расширения турбулентной струи. Докажем, что в такой постановке С, зависит от турбулизации атмосферы, т. е. от коэффициента расширения потока к.

Не нарушая общности, рассмотрим струйный поток плотности с круглого поперечного сечения, распространяющийся со скоростью V в неподвижной среде плотности р_е. Как известно, он имеет вид расширяющегося прямоугольного конуса с переменным углом расширения ? = arc tg k (в случае неизотропного потока углы его расширения

?_z = [?'²]^1/2 в направлении оси Z

и ?_у = [?'²]^1/2 в направлении оси Y,

где

?' и ?' — пульсации угла вектора скорости в вертикальной плоскости вдоль соответствующих направлений).

Будем вести рассмотрение элементарного газового объема струи, ограниченного нормальными к оси поперечными сечениями «1» и «2» и боковой поверхностью (Рис. 3.2).

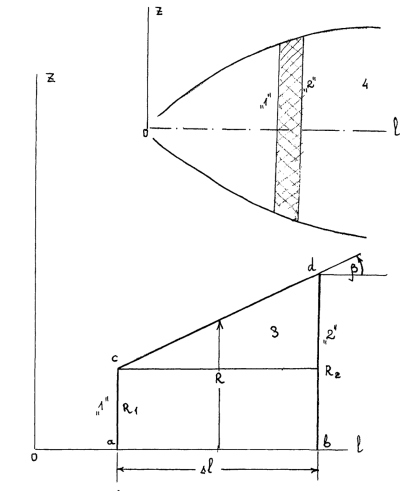
Рис. 3.2. Схема вертикального осевого сечения элементарного газового объема струи (на верхнем рисунке заштрихован): «1» и «2» — контрольные сечения, ограничивающие элементарный газовый объем; 3 — приращение газового объема при движении потока от сечения «1» к сечению «2»; 4 — неизотермическая струя.

Так как длина контрольного объема ?l — мала, то внешнюю его поверхность, контактирующую с воздухом окружающей среды, можно считать прямолинейной конической. Ее образующая на этом рисунке — линия cd.

Вычислим увеличение объема струи Av при ее развитии от сечения «1» к сечению «2». Из рисунка видно, что

Введем среднее или текущее значение радиуса усеченного конуса R и приращение радиуса AR по формулам:

Из решения системы алгебраических уравнений относительно переменных R и AR получаем:

R₂=R + ?R/2; R₁ = R — ?R/2. (3.8)

Вычислим выражение в квадратных скобках (3.6) при учете соотношений (3.8). Получаем:

R₂² — 2R₁ + R₁R_a = 3R?R (1– ?R/6R). (3.9)

Так как для развитого турбулентного потока ?R /R < 1, то ?R / 6R << 1 и вторым членом в скобках правой части (3.9) можно пренебречь по сравнением с 1. При этом объем кругового конического кольца ?v записывается так:

?v ? ?R?R?I. (3.10)

Преобразуем эту формулу при учете следующих геометрических соотношений:

S = ?R²; k = tg ? = ?R/?I.

Получаем

В этом соотношении:

S — площадь поперечного сечения контрольного газового элемента в некотором текущем или среднем сечении.

Масса кругового конического кольца с образующей cd находится из уравнения

?M = р?? (3.12)

где 

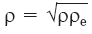
Так как AM в точности равна массе поступившего в струю вещества за счет вовлечения окружающего воздуха на пространственно-временном интервале ?l ?t:

?M = Е ?I ?t, (3.13)

то подставив в (3.13) вместо Е его выражение из (3.2), а вместо скорости его значение через дифференциалы ?I и ?t, получаем

Приравнивая AM из (3.12) и (3.13а), получаем:

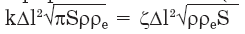
откуда

Из соотношения (3.14) следует, что вовлечение в струйный поток окружающего воздуха полностью определяется его угловым коэффициентом или углом расширения струи.

Найдем теперь связь углового коэффициента расширения клуба с коэффициентом вовлечения в него атмосферного воздуха ?_к. По аналогии с работой [96], в которой понятие вовлечения используется для струй, запишем выражение для вовлечения вещества в клуб в виде:_

Напомним физический смысл вовлечения — это масса окружающей среды, поступающая в выброс в единицу времени через его единичную поверхность; [Е] = кг/с/кв.м. Поэтому приращение массы выброса в виде клуба AM за интервал времени At запишется так:

?M = Е S ?t, (3.16)

где поверхность вовлечения

S = FR_m²;

Rm — усредненное за интервал ?t значение радиуса выброса;

F — коэффициент формы (для сферы F = 4n).

С другой стороны, приращение AM можно связать с приращением эффективного радиуса выброса (Рис. 3.3):

?M = ?_m F R_m² ?R, (3.17)

где ?_m — усредненное в слое AR значение плотности вещества выброса.

Приравниваем (3.16) и (3.17) при учете (3.5) и связи приращения пути выброса ?l со скоростью его движения:

?l = V ?t.

Получаем

Так как

то из (3.18) следует окончательная связь

?_к = к (3.19)

Из формулы (3.19) следует, что коэффициент вовлечения атмосферного выброса в виде компактного объема в точности равен его угловому коэффициенту в процессе расширения.

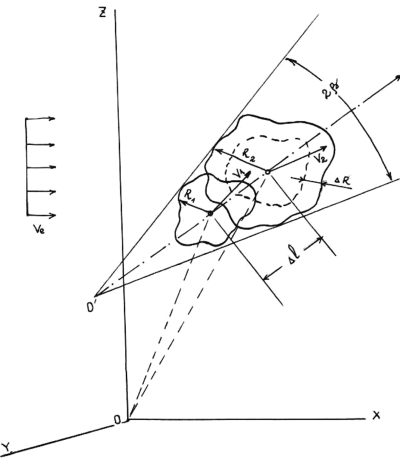
Рис. 3.3. Схема расширения клуба в атмосфере: «1» и «2» — пространственные положения клуба в моменты времени t₁ и t₂; 0 — виртуальный центр расширения выброса; ?R — приращение эффективного радиуса выброса за интервал времени ?t; 1 — ось траекторного движения клуба; ? ветровой поток;……. воображаемый контур клуба «2» в момент времени t₁.

Рассмотрим теперь, как по физическим (метеорологическим) характеристикам атмосферы определить ее устойчивость, характеристики расширения струйного потока и вовлечения в него окружающего воздуха.