Книга: Большое космическое путешествие

Глава 3 Законы Ньютона

Глава 3

Законы Ньютона

Автор: Майкл Стросс

Коперник совершил революционное открытие, объяснив движения планет в контексте гелиоцентрической Вселенной и поместив Солнце в центре Солнечной системы. Различные планеты, и Земля в том числе, движутся по околосолнечным орбитам. Мы сидим на движущейся платформе. Чтобы определить, как быстро движется Земля, мы должны определить, какое расстояние она проходит за конкретный интервал времени. В таком случае скорость будет равна расстоянию, деленному на время.

Как было рассказано в главе 2, Кеплер показал, что орбита Земли имеет форму эллипса. На самом деле орбиты большинства планет в нашей Солнечной системе близки к круговым, так что пока приблизительно условимся, что Земля движется по кругу и один такой круг проходит за год. Радиус этого круга, то есть расстояние от Солнца до Земли, постоянно используется в астрономии. Как было сказано в предыдущей главе, оно официально называется «астрономическая единица», сокращенно а.е. Одна а.е. равна примерно 150 миллионам километров, или 1,5 ? 10⁸ км.

Итак, за год Земля описывает окружность с радиусом 150 миллионов километров. Длина окружности равна 2? радиуса. Все знают, что число ? примерно равно 3. Примерно такими грубыми приближениями оперируют астрономы. Длину окружности нужно разделить на время, то есть на 1 год.

Пересчитаем год в секундах, впоследствии нам это пригодится. Количество секунд в году равно: 60 секунд в минуте умножить на 60 минут в часе, умножить на 24 часа в сутках, умножить на 365 дней в году. Можно посчитать на калькуляторе, но, как вы помните из главы 1, Нил отметил свою миллиардную секунду бутылкой шампанского, а было ему тогда около 31 года. Соответственно в году примерно 1/30 миллиарда, то есть около 30 миллионов секунд. Возьмем приблизительно 3,0 ? 10⁷ секунд в году.

Резюмируя, можно сказать, что Земля вращается вокруг Солнца со скоростью 2?r/(1 год) = 2 ? 3 ? (1,5 ? 10⁸ км)/(3 ? 10⁷ с) = 30 км/с. Вот с такой скоростью мы движемся вокруг Солнца прямо сейчас. Просто несемся! Но нам кажется, что мы спокойно сидим на месте, – возможно, именно поэтому древним казалось естественным ставить себя в центр Вселенной. Это представлялось столь очевидным. Но на самом деле можно заметить активное движение. За сутки Земля совершает полный оборот вокруг своей оси. За год она обходит полный путь вокруг Солнца со скоростью 30 км/с. Во второй части книги мы расскажем, что Солнце также движется (увлекая за собой Землю и другие планеты).

Коперник говорил, что планеты вращаются вокруг Солнца. Кеплер воспользовался расчетами Тихо Браге, определив с их помощью орбиты разных планет и изучив их свойства. Как упоминалось в главе 2, он вывел из этого три закона. Исаак Ньютон, один из героев нашей истории, смог вывести из третьего закона Кеплера такое следствие: притяжение – это радиальная сила между двумя объектами, обратно пропорциональная квадрату расстояния между ними.

Пожалуй, Ньютон был величайшим физиком, возможно, самым великим из когда-либо живших ученых. Он совершил множество фундаментальных открытий. Ньютон хотел понять, как движется все на свете: не только планеты вокруг Солнца, но и мяч, подброшенный в воздух, или камень, катящийся по склону.

В науке требуется сделать множество измерений, а потом попытаться вывести из них небольшое количество законов, которые обобщают и объясняют эти наблюдения. Ньютон сформулировал три закона движения. Первый закон Ньютона – это закон инерции. Что такое инерция? Есть такое выражение «плыть по течению»; оно означает, что вам совершенно не хочется противиться инерции. Лежишь себе на диване и не рыпаешься. Вас кто-то должен подтолкнуть, чтобы вы встали с дивана. Объект в состоянии покоя (например, лежебока) так и останется в покое, пока на него не подействует внешняя сила.

Обсудим, что такое сила. Закон Ньютона об инерции состоит из двух частей. Первая часть: «всякое тело сохраняет состояние покоя до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние». Это логично. Допустим, лежит на столе яблоко. На него не действует никакая сила, поэтому оно остается в покое.

Вторая часть ньютоновского закона об инерции формулируется не столь очевидно: «объект, равномерно движущийся с определенной скоростью, продолжит двигаться с той же скоростью, пока на него не подействует внешняя сила». «Равномерно» означает с одной и той же скоростью, в одном и том же направлении. Если запустить мячик по полу, то он не будет двигаться в этом направлении вечно и с постоянной скоростью, а замедлится и остановится. Ведь на него действует третья сила – трение между мячиком и полом. В обыденной жизни трение встречается повсеместно. Допустим, вы пустили по воздуху лист бумаги; он замедлится, а затем спланирует на пол. В полете на него действуют две силы: 1) сила гравитации, о которой мы вскоре подробно поговорим, и 2) сила сопротивления воздуха. Площадь листа бумаги велика, поэтому и сопротивление воздуха получается значительным.

Идея о том, что движущееся тело так и будет двигаться с постоянной скоростью, если на него не действуют внешние силы, не очевидна, так как мы повсюду сталкиваемся с трением. Сложно вообразить обыденную ситуацию, в которой отсутствует всякое трение и, соответственно, нет воздействия внешних сил. Фигуристка почти не испытывает трения между коньками и льдом, поэтому она может сравнительно легко прокатываться по льду на большие расстояния. Когда трение стремится к нулю, объект достаточно подтолкнуть – и он станет двигаться с постоянной скоростью. Галилей это понял. Открытый космос предлагает самые яркие примеры отсутствия какого-либо трения. В космосе действительно можно запустить объект и не сомневаться, что он так и полетит равномерно с этой скоростью, поскольку ничто не встретится ему на пути. Ньютон сформулировал все эти принципы в виде базового закона.

Второй закон движения Ньютона описывает, что происходит с объектом, на который воздействует сила. На объект могут действовать разнообразные силы, но, независимо от конкретных сил, именно их сумма дает отклонение от равномерной скорости. Чтобы количественно выразить такое отклонение, используется термин «ускорение»: ускорение – это изменение скорости за единицу времени. Следовательно, второй закон соотносит ускорение объекта с силой, действующей на него. Если подтолкнуть объект с некоторой силой, то объект ускорится. Если объект обладает небольшой массой, то ускорение будет велико; с другой стороны, приложив ту же силу к более массивному объекту, мы сообщим ему меньшее ускорение. Данное отношение описывается самым знаменитым уравнением Ньютона F= ma: сила равна произведению массы на ускорение.

Третий закон Ньютона можно «запросто» сформулировать так: «Ты толкаешь меня – я толкаю тебя». Таким образом, если одно тело с силой воздействует на другое, то второе тело воздействует на первое с равной, но противоположно направленной силой. Если хлопнуть рукой по столешнице, то ощущается отдача: сопротивление стола. Сила действия равна силе противодействия.

Допустим, у вас на ладони лежит яблоко. Определенно оно находится в покое. Действуют ли на него какие-либо силы? Да, земная гравитация. Яблоко должно с ускорением лететь вниз, но этого не происходит. Дело в том, что вы удерживаете его рукой, словно подталкиваете вверх (на это затрачивается ваша мышечная сила). По третьему закону Ньютона, яблоко давит на ладонь – так ощущается вес яблока. Сила притяжения Земли действует на яблоко вниз, а сила вашей руки толкает яблоко вверх. Две эти силы компенсируют друг друга, их сумма равна нулю. Нулевая сила означает нулевое ускорение по второму закону Ньютона. Поэтому яблоко остается в покое и никуда не катится.

На самом деле все еще интереснее. Выше мы вычислили, что Земля облетает Солнце по кругу со скоростью 30 км/с, а значит, и яблоко движется с той же скоростью. Чтобы разобраться с этим, давайте сделаем отступление и поговорим о природе кругового движения.

При движении Земли по кругу со скоростью 30 км/с ее скорость является постоянной, но не является равномерной, так как направление движения Земли постоянно изменяется. Если бы направление не менялось, то Земля бы просто улетела по прямой, а не вращалась по кругу. Ускорение, возникающее при движении по кругу, встречается и в повседневной жизни. В развлекательных парках есть разнообразные аттракционы-горки, и на них такое ускорение пробирает вас насквозь.

Чтобы определить ускорение, испытываемое объектом, который движется с постоянной скоростью v по кругу радиусом r, Ньютон воспользовался собственноручно изобретенным дифференциальным исчислением. Такое ускорение равно v²/r, оно направлено к центру круга. Яблоко у вас на ладони, которое кажется неподвижным, на самом деле летит со скоростью 30 км/с по этому колоссальному кругу, причем с ускорением. По второму закону Ньютона на яблоко должна действовать какая-то сила, и эта сила – гравитационное притяжение Солнца. Солнце тащит Землю по орбите со скоростью 30 км/c, а вместе с ней тащит и яблоко. Яблоко испытывает силу солнечной гравитации, точно как вы и я.

Мы летим вокруг Солнца со скоростью 30 км/c. Учитывая, как велика эта скорость, кажется, что результирующее ускорение также должно быть огромным, но ускорение на самом деле невелико, поскольку радиус круга огромен. Давайте посчитаем. Скорость Земли равна 30 км/c или 30 000 м/c, а радиус земной орбиты – 150 000 000 000 м. По формуле v²/r ускорение a равно (30 000 м/c)²/150 000 000 000 м = 0,006 м/с², или 0,006 метра в секунду за секунду. Таким образом, скорость Земли ежесекундно меняется на 6 миллиметров в секунду. Величина крошечная. Галилей открыл, что тела падают на Землю под действием земного притяжения с ускорением примерно 9,8 метра в секунду за секунду, это значение гораздо больше. Следовательно, пусть мы и летим вокруг Солнца с огромной скоростью, Земля при этом ускоряется совершенно незначительно. Напротив, на американских горках наша скорость куда ниже 30 км/c, но радиус круга, по которому мы движемся, крохотный; подставив это меньшее значение r в формулу v²/r, получаем довольно большое ускорение, которое весьма ощутимо. (Так, если радиус горок – 10 метров, а вы летите по ним со скоростью 10 м/c, то получается ускорение 10 метров в секунду за секунду).

Если попытаться проследить гравитационное воздействие Солнца, то складывается более тонкая ситуация. Солнечная гравитация сообщает одинаковое ускорение всем телам на Земле – вам, книге, которую вы держите, яблоку на ладони. Все мы вращаемся по околосолнечной орбите свободного падения. Нам только кажется, что мы неподвижны; просто мы не замечаем этого движения, равно как не замечаем и ускорения.

Но факт остается фактом: Земля вращается вокруг Солнца с ускорением, и это ускорение вычисляется по формуле v²/r. Далее Ньютон применил третий закон Кеплера, чтобы определить, как сообщаемое Солнцем ускорение изменяется в зависимости от радиуса. Период орбитального вращения планеты (P) равен

P = (2?r/v);

следовательно, орбитальный период вычисляется как расстояние, проходимое планетой по орбите (2?r), деленное на скорость (v). Таким образом:

P пропорционально r/v и

P² пропорционально r²/v².

Кеплер установил, что P² пропорционально a³, где a — большая полуось планетной орбиты. В данном случае земная орбита почти круговая, поэтому можно приблизительно взять r = a. В таком случае, подставив r вместо a, находим:

P² пропорционально r³.

ПосколькуP² также пропорционально r²/v²,

r²/v² пропорционально r³.

Разделив на r, получаем:

r/v² пропорционально r².

Обратив это выражение, находим, что

v²/r (ускорение) пропорционально 1/r².

При помощи таких рассуждений, третьего закона Кеплера и элементарной алгебры мы показали, что гравитационное ускорение, сообщаемое Солнцем другому телу, удаленному от него на расстояние r, обратно пропорционально квадрату этого расстояния; это и есть ньютоновский «закон обратных квадратов». Вот как его сформулировал сам Ньютон:

Такие представления о гравитации Ньютон также применил к Земле и Луне. Вспомните знаменитое упавшее яблоко, вдохновившее Ньютона. Оно расположено на расстоянии одного земного радиуса от центра Земли и падает на Землю с ускорением 9,8 м/с². Луна расположена на расстоянии 60 земных радиусов от центра Земли. Если сила тяготения Земли убывает в пропорции 1/r² (как и у Солнца), то на лунной орбите земное притяжение должно давать ускорение в (60)² раз меньше тех 9,8 м/с², которым равно ускорение свободного падения на поверхности Земли, то есть около 0,00272 метра в секунду за секунду.

Точно как и в случае с вращением Земли вокруг Солнца, можно рассчитать ускорение Луны, вращающейся вокруг Земли, взяв период вращения (27,3 дня) и радиус лунной орбиты (384 000 километров). Подставив эти числа в формулу v²/r, получаем ускорение 0,00272 метра в секунду за секунду. Эврика! Как красиво все согласуется с моделью, где расчет велся от яблока. По словам самого Ньютона, два этих результата показались ему «весьма близко совпадающими». Одна и та же сила притягивает к Земле и яблоко, и Луну, причем траектория Луны искривляется и становится не прямолинейной, а круговой, что позволяет ей удерживаться на приблизительно концентрической околоземной орбите. Сила земного притяжения, под действием которой падает яблоко, распространяется и на орбиту Луны. Ньютон совершил это открытие, когда жил в доме бабушки, – Кембриджский университет в те годы был закрыт из-за чумы. Но он не опубликовал результаты своей работы. Вероятно, он был раздосадован, что наблюдения не вполне согласовывались с прогнозом – небольшое расхождение могло быть связано с тем, что Ньютон пользовался неточным значением земного радиуса. Как бы то ни было, опубликовать эти расчеты лишь много лет спустя уговорил Ньютона Эдмунд Галлей (в честь которого названа комета).

Ньютон сформулировал закономерность, которую часто называют пафосным выражением «Закон всемирного тяготения» – с ним вы познакомились в главе 2. Рассмотрим два объекта – например, Землю и Солнце. Расстояние между ними (1 а.е., или 1,5 ? 10⁸ км) примерно в 100 раз превосходит диаметр самого Солнца (1,4 ? 10⁶ км). Эти тела обладают соответственно массами M_ЗЕМЛ и М_СОЛН.

Ньютон обнаружил, что сила притяжения между двумя этими телами пропорциональна массе каждого из них и обратному квадрату расстояния r между ними (как я уже говорил, он пришел к такому выводу, опираясь на третий закон Кеплера). «Пропорциональна» в данном случае означает, что сила будет включать константу, характеризующую пропорциональность, – она называется G, или «постоянная Ньютона», в честь сэра Исаака. Вот формула Ньютона, описывающая тяготение между Солнцем и Землей:

F = GM_ЗЕМЛМ_СОЛН/r².

Речь идет о силе притяжения; два тела притягиваются друг к другу, и, следовательно, эта сила направлена от первого тела ко второму и от второго к первому.

По третьему закону Ньютона эта формула охватывает как силу притяжения Земли к Солнцу, так и силу притяжения Солнца к Земле. Но Солнце неизмеримо массивнее Земли. По второму закону Ньютона ускорение есть сила, деленная на массу. Следовательно, ускорение Земли гораздо, гораздо больше ускорения Солнца, и скорость, сообщаемая Солнцу из-за такого ускорения, крошечная по сравнению со скоростью Земли (Солнце и Земля вращаются вокруг общего центра масс, но он находится под поверхностью Солнца. Солнце минимально колышется вокруг этого центра, тогда как Земля описывает вокруг Солнца большой круг).

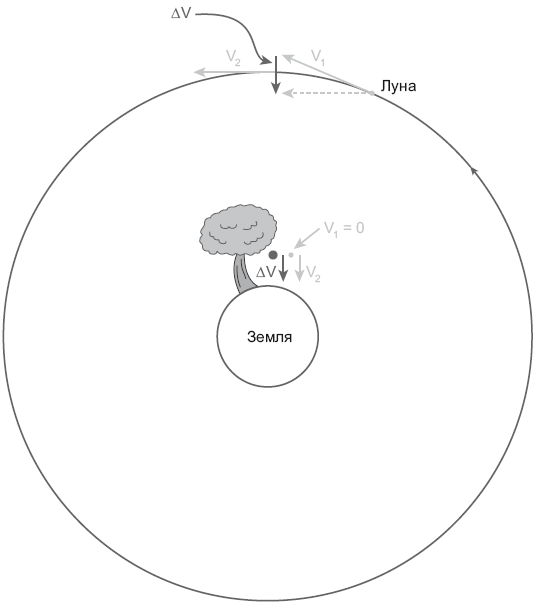
Рис. 3.1. Ускорение Луны и ньютоновского яблока, падающего с дерева. Обратите внимание: в обоих случаях вектор ускорения (изменения скорости) направлен к центру Земли. Предоставлено Дж. Ричардом Готтом

Рассмотрим еще одно удивительное следствие из формулы Ньютона. По второму закону Ньютона сила гравитации, формулу которой мы записали чуть выше, равна произведению массы Земли (M_ЗЕМЛ) на ее ускорение, а при движении по кругу ускорение равно v²/r. Таким образом, формулу F = ma можно переписать:

GM_ЗЕМЛМ_СОЛН/r²= M_ЗЕМЛv²/r.

Обратите внимание: масса Земли присутствует и в левой, и в правой части тождества, поэтому ее можно сократить, и останется:

GМ_СОЛН/r²= v²/r.

Это означает, что ускорение Земли (GМ_СОЛН /r²= v²/r) не зависит от массы Земли. Это примечательный факт. Ускорение силы тяжести не зависит от массы ускоряющегося объекта, это касается и околосолнечных орбит, и тел, падающих на Землю в ее гравитационном поле, – все потому, что масса тела оказывается и в левой, и в правой части уравнения и, соответственно, сокращается. Если я брошу книгу и лист бумаги, то они будут испытывать одно и то же ускорение и должны падать с одинаковой скоростью, хотя книга гораздо массивнее. Галилей утверждал, что именно так и должно быть в вакууме. Так ли это на практике? Нет, книга и лист падают с разной скоростью из-за сопротивления воздуха. Сопротивление воздуха воздействует как на книгу, так и на лист, но поскольку книга гораздо массивнее, сопротивление воздуха ускорению книги будет невелико – в сущности, пренебрежимо. Однако если я положу лист бумаги на толстую книгу, так чтобы книга исключала соприкосновение листа бумаги с воздухом, и брошу их как одно целое, то они упадут вместе. Можете сами проверить!

Когда астронавты экипажа «Аполлона-15» прибыли на Луну, они захватили с собой молоток и перо, чтобы экспериментально проверить этот принцип. На Луне практически нет атмосферы; у ее поверхности – самый настоящий вакуум, соответственно никакого сопротивления воздуха там не будет. Когда астронавты одновременно бросали молоток и перо, те падали абсолютно синхронно, точно как прогнозировал Ньютон (и Галилей). В Интернете можно посмотреть видеозапись этого эксперимента.

Возможно, вам известно, что Аристотель в данном случае ошибался. Он считал, что более массивные тела должны падать быстрее и с большим ускорением. Это казалось ему логичным, но на самом деле он ни разу не поставил эксперимент, чтобы проверить, а верна ли эта идея. Он мог бы взять камень побольше и камень поменьше (ни на один камень сопротивление воздуха практически не действует), бросить их и убедиться, что оба камня упадут практически одновременно. Вывод: в науке исключительно важно экспериментально проверять любые интуитивные догадки!

Рассмотрим смежную проблему. Сила тяготения Земли воздействует на яблоко, которое вы держите в поднятой руке. В формуле Ньютона есть величина r – расстояние от яблока до Земли. Можно было бы подумать, что здесь имеется в виду расстояние от яблока до пола, около 2 метров. Оказывается, это неверно. Ньютон осознал, что нужно учитывать притяжение каждого грамма земной массы; не только той, что у вас под ногами, но и всей остальной, вплоть до противоположного полушария. Ему потребовалось около 20 лет, чтобы выполнить такие вычисления. Пришлось сложить силы притяжения каждого отдельного кусочка Земли, у каждого из которых – свое расстояние и направление от яблока. Для сложения всех этих сил потребовалось изобрести совершенно новую область математики, сегодня именуемую интегральным исчислением. Результат такого вычисления показывает, что гравитация шарообразного тела (например, Земли) действует так, как будто вся масса сконцентрирована в центре этого тела, – интуитивно совершенно не очевидно. Чтобы вычислить силу тяготения, действующую на яблоко, нужно представить, что вся масса Земли локализована в одной точке на глубине 6371 километров – таково расстояние от поверхности до центра Земли. Мы уже пользовались таким методом, когда сравнивали падающее яблоко и вращающуюся на орбите Луну.

Но вертикальное падение яблока (прямо вниз) определенно не похоже на орбитальное вращение Луны. Почему Луна летает кругами, а яблоко просто падает на землю? Чтобы забросить яблоко на орбиту, мне бы пришлось горизонтально швырнуть его по прямой так сильно, чтобы оно могло облететь всю Землю. Есть, например, космический телескоп «Хаббл», летающий всего в нескольких сотнях километров над поверхностью Земли. Примерно за полтора часа он облетает околоземную орбиту, окружность длиной около 40 тысяч километров. Можно вычислить его скорость – где-то 8 километров в секунду. Итак, чтобы забросить яблоко на орбиту, нужно швырнуть его строго по горизонтали со скоростью восемь 8 в секунду.

Предположим, вы стоите на вершине высокой горы (где эффект трения атмосферы уже можно не учитывать) и бросаете объекты по горизонтали на все более высокой скорости. Бросьте яблоко так сильно, как сможете, – и оно почти сразу упадет на землю. Пригласите для броска бейсболиста-профессионала – он кинет яблоко немного дальше, но оно все равно упадет. Теперь пусть яблоко бросит Супермен. Он будет бросать все сильнее и сильнее, яблоко будет долетать все дальше, пока криволинейная траектория яблока не упрется в землю. Но поверхность Земли не плоская; на больших расстояниях становится заметно, что она также изгибается книзу. Супермен действительно может швырнуть яблоко так, чтобы оно летело со скоростью 8 километров в секунду. Такой объект также будет падать под действием гравитации, но его криволинейная траектория будет повторять кривизну Земли. Поэтому этот объект так и не упадет, а окажется на круговой околоземной орбите. Объект на орбите все время падает и при этом не попадает на Землю. Когда вы бросаете яблоко, оно падает под действием земного тяготения. Благодаря все тому же тяготению Земли, и космический телескоп «Хаббл», и Луна вращаются вокруг Земли (орбита Луны гораздо выше, поэтому Луна движется намного медленнее). На низкой околоземной орбите вы падаете со скоростью вращения Земли, поэтому так и не можете упасть. Ньютон понимал это и теоретически описал искусственный спутник Земли – за 270 лет до того, как спутник был сконструирован!

Если вам доводилось ехать на лифте, который вдруг резко уходил вниз, то в течение какого-то мига вы ощущали, что падаете и все вокруг падает вместе с вами. Если бросить яблоко, то оно упадет, а вы нет, так как вас держит земля под ногами. Вы остаетесь в покое относительно окружающих предметов, а яблоко падает под действием гравитационного ускорения. Если бы вы держали в руке яблоко, а вас при этом сшибли с ног, то вы бы увидели, как падаете вместе с яблоком (пока не очутились бы на полу).

Вероятно, вы видели снимки астронавтов, работающих на Международной космической станции на околоземной орбите. Земное притяжение действует как на астронавтов, так и на МКС. Но все тела в пределах МКС падают с одинаковой скоростью – вспомните наши расчеты, демонстрирующие, что гравитационное ускорение не зависит от массы объекта, находящегося на орбите. Когда все падает с одинаковой скоростью, астронавты ощущают невесомость. «Вес» фиксируется на обычных напольных весах, когда вы на них стоите (или, что эквивалентно, фиксируется отдача весов по третьему закону Ньютона). Но если вы падаете вместе с весами, то не давите на них – они покажут «0». Вы будете невесомы.

Это, однако, не означает, что ваша масса равна нулю. Масса и вес не одно и то же! Масса, по Ньютону, – это величина, учитываемая во втором законе движения (где соотносятся силы, массы и ускорение); именно благодаря этой величине возникает и тяготение. Когда кто-то говорит, что «хочет избавиться от лишнего веса», на самом деле он хочет сбавить собственную массу. Жир имеет массу, именно от жира человек и избавляется. Тогда, прилагая прежние усилия, человек легче ускоряется и начинает свободнее двигаться.

Давайте подытожим достижения Ньютона. Изучая движения планет, известных на то время, Кеплер вывел три закона, описывающих планетные орбиты. Затем явился Ньютон и совершенно переосмыслил открытия Кеплера; сформулировав три своих закона движения, он пытался понять, как движется все на свете, а не только шесть планет, вращающихся вокруг Солнца. Кроме того, он подвел физическую базу под силу тяготения – важнейшую силу в астрономии. Воспользовавшись третьим законом Кеплера, он показал, что сила тяготения должна ослабевать по формуле 1/r². Он обнаружил, что два тела, пребывающие в гравитационном взаимодействии, притягиваются друг к другу; так, гравитационное взаимодействие Солнца и любой планеты вычисляется по формуле F = GМ_СОЛНM_ПЛАН/r². Резюмируя все это, видим, что третий закон Кеплера можно выразить на уровне ньютоновских законов движения и закона тяготения. Ньютон предложил гораздо более обширное понимание физики, лежащей в основе третьего закона Кеплера, нежели сам Кеплер.

Окончательный триумф Ньютона наступил, когда подтвердилось, что по третьему закону движения планета должна двигаться по идеально эллиптической орбите, причем в одном из фокусов эллипса находится Солнце, а также что линия, проведенная между планетой и Солнцем, будет заметать равные площади за равные промежутки времени. Теперь все три закона Кеплера можно было напрямую вывести из единственного закона гравитационного притяжения, сформулированного Ньютоном, плюс трех его законов движения.

Ньютоновские законы тяготения были первыми физическими законами, которые мы поняли. Важно, что на их основе можно было делать проверяемые прогнозы. Галлей воспользовался законами Ньютона и открыл, что несколько комет, прилетавших в течение веков (в том числе комета 1066 года, изображенная на гобелене из Байё), – это в действительности одна и та же комета, вращающаяся по очень вытянутой эллиптической орбите. Она прилетает примерно раз в 76 лет. На ее движение влияют Юпитер и Сатурн, так как комета пересекает их орбиты, и слегка варьирующиеся сроки прибытия этой кометы можно предсказать при помощи законов Ньютона, тогда как, по законам Кеплера, вращение этой кометы должно быть строго периодическим. Галлей указал, что комета должна вернуться в 1758 году. Он умер в 1742 году, не дождавшись этого события, но комета действительно явилась в 1758 году и уже в следующем году была названа кометой Галлея. Приближение кометы к Солнцу на минимальное расстояние с точностью до месяца смогли спрогнозировать Алекси Клеро, Жером Лаланд и Николь-Рейн Лепот, воспользовавшиеся законами Ньютона. Это было блестящее подтверждение ньютоновских законов тяготения.

Законы Ньютона помогли совершить еще одно выдающееся открытие. Планета Уран не вполне им подчиняется; ее орбита кажется немного искривленной. Урбен Леверье обнаружил, что эти отклонения можно объяснить, если Уран испытывает тяготение некоей невидимой планеты, расположенной еще дальше от Солнца. Он спрогнозировал, где может находиться эта планета, и в 1846 году Иоганн Готфрид Галле и Генрих Луи д’Арре, воспользовавшись расчетами Леверье, нашли эту планету лишь в 1° небесной сферы от указанной им точки. Законы Ньютона помогли открыть новую планету – Нептун. Репутация Ньютона достигла запредельных высот.

Читая эту книгу и пытаясь постичь Вселенную, мы будем вновь и вновь обращаться к этим базовым понятиям, описывающим силу и тяготение.