Книга: Большое космическое путешествие

Глава 5 Как звезды излучают энергию (II)

Глава 5

Как звезды излучают энергию (II)

Автор: Нил Деграсс Тайсон

Теперь давайте отправимся в большую Вселенную. В главе 4 мы рассмотрели графики теплового излучения звезд. На рис. 5.1 изображена очень похожая диаграмма, но с некоторыми дополнениями. По оси ординат откладывается интенсивность (мощность на единицу площади на единичный интервал длин волн), а по оси абсцисс – длина волны (увеличивается слева направо). Часть спектра, которую мы именуем «видимый свет», как и выше, обозначена радужной полосой.

На рисунке показаны кривые теплового излучения для Солнца (температура 5800 К), горячей звезды (температура 15 000 К), холодной звезды (3000 К) и человека (310 К). Пик кривой теплового излучения человека находится на уровне около 0,001 см. Гораздо ниже и правее этой кривой находим новую кривую – график, соответствующий средней температуре примерно 2,7 К. Это температура всей Вселенной! Именно такой температурой обладает знаменитое реликтовое излучение, льющееся на нас со всего неба. Поскольку его пик относится к микроволновой части спектра, его также называют «космический микроволновый фон». Реликтовое излучение было открыто в штате Нью-Джерси, в Bell Laboratories в середине 1960-х годов. Арно Пензиас и Роберт Вильсон работали с радиотелескопом, который называли «микроволновая рупорная антенна». Направив радиотелескоп в небо, они обнаружили, что отовсюду поступает микроволновый сигнал, и температура такого излучения должна составлять около 3 К (по современным уточненным данным, эта величина равна 2,725 К). Это тепловое излучение, сохранившееся после Большого взрыва. Мы гораздо подробнее поговорим об этом в главе 15.

Как и в предыдущем случае, эти графики можно рассматривать по-разному. Где пик каждой кривой? Эти пики расположены в разных местах. Сколько всего энергии излучается в секунду? Нужен способ просуммировать площадь под каждой кривой и определить, сколько всего энергии в секунду излучается в данном случае. Во-первых, давайте определимся с терминами.

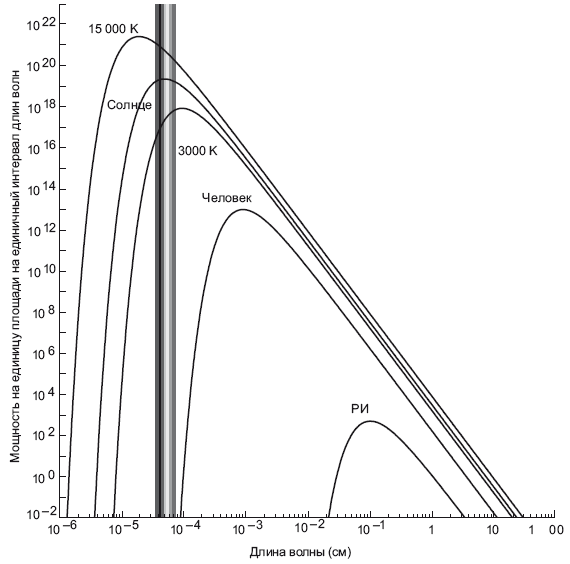
Рис. 5.1. Тепловое излучение Вселенной. Спектры абсолютно черных тел, имеющих разную температуру, показаны как функции длины волны. По оси ординат откладывается энергия в единицу времени (то есть мощность), излучаемая различными объектами на единицу поверхностной площади при заданной температуре; единицы выбраны произвольно. Кривые соответствуют звездам с поверхностной температурой около 15 000 К (такая звезда покажется голубовато-белой), 5800 К (таково Солнце, которое покажется белым) и 3000 К (такая звезда покажется красной). Видимая часть спектра обозначена как радужная полоса. Также приведены графики излучения человеческого тела (310 К) и реликтового излучения (РИ, 2,7 К). О реликтовом излучении мы подробнее поговорим в главе 15. Предоставлено Майклом Строссом

Абсолютно черное тело – это объект, поглощающий все входящее излучение. Абсолютно черное тело, имеющее определенную температуру, будет испускать так называемое «излучение черного тела», повторяющее контуры рассматриваемых кривых. Термин «абсолютно черное тело» может показаться неудачным, но это не так. Никто не спорит, что звезды – не черные; одна звезда сияет голубым, другая – белым, третья – красным. Но все они считаются абсолютно черными телами, как я и показал на рисунке. Абсолютно черное тело устроено просто: оно поглощает всю энергию, которую получает. Оно всеядно. Ему по вкусу и гамма-лучи, и радиоволны. Черные предметы поглощают всю попадающую на них энергию. Вот почему летом не стоит наряжаться в черное. Затем абсолютно черные тела переизлучают эти кривые – вот и всё. Контур и положение кривой зависят лишь от температуры абсолютно черного тела.

Можно нагреть предмет, повысить его температуру, а затем останется определить: какова новая температура? Затем мы возвращаемся к нашим кривым и смотрим, какой график соответствует новой температуре. Есть чудесное уравнение, описывающее эти кривые. Они являются функциями распределения и также именуются планковскими функциями в честь Макса Планка, который первым вывел уравнения для них. В правой части уравнения имеем энергию в единицу времени на единицу площади на единичный интервал длин волн при конкретной длине волны; эта величина называется «интенсивность» (I?) и зависит только от температуры T абсолютно черного тела:

I_? (T) = (2hc²/ ?⁵)/(e^hc/ ?^kT – 1).

Давайте разберемся, какие элементы входят в это эпохальное уравнение. Во-первых, здесь есть ? (лямбда), это длина волны, с ней все понятно. Постоянная e – это основание натуральных логарифмов, под нее выделена специальная клавиша на любом инженерном калькуляторе, на которой обычно написано «e^x» (e в степени x). Значение числа e равно 2,71828…; как и в числе ?, в нем бесконечное количество десятичных знаков. Это просто число. Буква c означает скорость света, с ней мы уже встречались. Буква k – это постоянная Больцмана. Буква T – это просто температура, а буква h означает постоянную Планка, с которой мы познакомились в главе 4. Если присвоить объекту температуру T, то единственным неизвестным в уравнении остается ? – длина волны. Так, постепенно присваивая ? разные значения, от очень малых до очень больших, мы получаем значение I_?. Это будет функция от длины волны, строго повторяющая показанные кривые. Макс Планк предложил это уравнение в 1900 году, и оно произвело революцию в физике.

Предложив свою постоянную, Планк положил начало квантовой физике; в то же время Макс Планк является и отцом-основателем квантовой механики. Обратите внимание на первый член в скобках: 2hc²/?⁵. Что происходит с энергией по мере увеличения длины волны? Она падает. С ростом ? член 1/?⁵ стремится к нулю. При больших ? член hc/?kT уменьшается. Математик сказал бы, что e^xпо мере уменьшения x становится примерно равен 1 + x.Так, при больших ? член hc/?kT уменьшается, а член e^hc/?^kTстановится примерно равен 1 + hc/?kT, и, если вычесть отсюда 1, член (ehc/?kT–1) становится равен hc/?kT. Соответственно в пределе, когда ? становится большим, все выражение приобретает вид I?(T) = (2hc²/?⁵)/(hc/?kT)= 2ckT/?⁴. Это тождество было известно и до Планка. Оно называлось «Закон Рэлея – Джинса» в честь открывших его лорда Рэлея и сэра Джеймса Джинса. По мере роста ? интенсивность I? начинает падать в строгом соответствии с формулой 1/?⁴.Что происходит, когда мы двигаемся в сторону все более коротких волн? По мере уменьшения ?⁴ 1/?⁴ возрастает, в результате чего уравнение рушится (перестает согласовываться с экспериментами). В свое время это явление было названо «ультрафиолетовая катастрофа». Здесь явно была какая-то ошибка. Вильгельм Вин сформулировал закон, объяснявший экспоненциальный спад при малых длинах волн и согласовывавшийся с данными в коротковолновом диапазоне, но не согласовывавшийся в длинноволновом. Мы не имели четкого представления об этих температурных кривых абсолютно черного тела вплоть до 1900 года, когда Макс Планк вывел формулу, согласовывавшуюся с данными и в коротковолновом, и в длинноволновом пределе спектра, а также везде между ними. Формула содержит постоянную h, которая позволяет квантовать энергию так, что любая энергия учитывается в виде дискретных пучков. Если трактовать энергию как дискретные пучки, то по мере перехода ко все более коротким волнам формула Планка начинает возрастать по экспоненте и член 1/?⁵ превращается в ничто. Когда ? мала, hc/?kT возрастает, а число e, возведенное в такую степень (e^hc/?^kT), очень быстро становится очень большим. Оно настолько больше –1, что этот член можно игнорировать, а при e^hc/?^kTв знаменателе ответ получается маленьким. Две эти части уравнения, член 1/?⁵ и член 1/e^hc/?^kT, словно состязаются друг с другом. По мере того как ? стремится к нулю, 1/e^hc/?^kTстремится к нулю гораздо быстрее, чем успевает расти член 1/?⁵, поэтому и вся кривая стремится к нулю. Без экспоненциального члена вся формула быстро устремилась бы к бесконечности, а длина волны – к нулю, но эксперименты показывают, что на практике это не подтверждается. Феномен кванта потребовался, чтобы понять природу теплового излучения, и уравнение Планка объясняет устройство этих кривых.

Формула Планка позволила все это учесть. Она верно показывает, где будет пик кривой. Исаак Ньютон изобрел математику, позволяющую вычислить пик функции: там, где крутизна кривой стремится к нулю при максимальном значении этой кривой. Ньютоновское дифференциальное исчисление позволяет взять производную функции и найти это место. В таком случае получим очень простой ответ: ?_пик = C/T, где C – новая константа, которую можно вывести из констант исходного уравнения. C = 2,898 мм, если T выражена в кельвинах. Где будет пик? Если T = 2,7 К, как в случае с РИ, то ?_пик будет чуть выше 1 мм или 0,1 см. Можно в этом убедиться, сверившись с кривой РИ на рис. 5.1. Человек примерно в 100 раз горячее; пик человеческого излучения приходится примерно на 0,001 см (см. рис. 5.1), в инфракрасном диапазоне.

Это красиво. С повышением температуры постоянно уменьшается длина волны, при которой кривая достигает пикового значения. Чтобы в этом убедиться, достаточно всего лишь рассмотреть свойства уравнения ?_пик = C/T. При T в знаменателе имеем, что вдвое более горячее тело даст пик функции при вдвое меньшей длине волны (эту зависимость обнаружил Вильгельм Вин, поэтому она называется «закон Вина»).

Как определить общую энергию на единицу времени на единицу поверхности, соответствующую площади под одной из этих кривых? Мне потребовалось бы просуммировать вклад от всех различных длин волн, то есть всю площадь под конкретной кривой. Для этого можно воспользоваться интегральным исчислением – опять же, спасибо Исааку Ньютону. Если интегрировать функцию Планка по всем длинам волн, то получится еще одно красивое уравнение.

Общая энергия, излучаемая в секунду на единицу площади = ?T⁴, где ? = 2?⁵k⁴/(15c²h³) = 5,67 ? 10^–8 ватт на квадратный метр, причем T – это температура в кельвинах. Перед нами закон Стефана – Больцмана. Йозеф Стефан и Людвиг Больцман были двумя титанами физики XIX века. К сожалению, Больцман свел счеты с жизнью, когда ему было 62 года. Но сохранился этот закон. Если интегрировать функцию Планка, то получится значение постоянной (греческая буква «сигма»). Это колоссально. Как Стефану и Больцману удалось сформулировать этот закон, если Планк еще не вывел свою формулу? Стефан открыл закон экспериментально, а Больцман сформулировал, исходя из соображений о термодинамике.

Если общая энергия, излучаемая в секунду на единицу площади равна ?T⁴, то, если удвоить температуру, поток излучаемой энергии возрастет с коэффициентом 2⁴ = 16.Утроим температуру, и что получится? 3⁴ = 81.Учетверим – и получится 4⁴ = 256.Эта тенденция прослеживается на рис. 5.1, где видно, насколько увеличиваются кривые при возрастании температуры.

Вот как можно запомнить принцип работы этой формулы. Допустим, мы взяли какое-то количество теплового излучения и положили его в коробочку. Теперь будем медленно сжимать коробочку, пока она не станет вдвое меньше. Количество фотонов в коробочке останется тем же, но объем коробочки уменьшится в 8 раз и, соответственно, количество фотонов на кубический сантиметр возрастет в 8 раз. Но при сжатии коробочки длина волны каждого фотона также укорачивается вдвое. В результате тепловое излучение коробочки становится вдвое жарче, так как пиковое значение длины волны уменьшилось вдвое. Удваивается энергия каждого фотона и, соответственно, энергия коробочки. Увеличение энергии каждого фотона происходит за счет той энергии, что затрачивается на сжатие коробочки, эта энергия противодействует давлению излучения, что внутри коробочки. Таким образом, плотность энергии в коробочке будет в 8 ? 2 = 16 раз выше, чем ранее, а 16 = 2⁴. Следовательно, энергетическая плотность теплового излучения пропорциональна температуре в четвертой степени, или T⁴.

Давайте определимся еще с некоторыми терминами. Светимость – это общая энергия, излучаемая звездой в единицу времени. Светимость измеряется в ваттах, точно как у лампочки накаливания. Светимость 100-ваттной лампочки равна 100 ватт. Светимость Солнца равна 3,8 ? 10²⁶ ватт. Мощная такая лампочка.

Теперь предложу задачку. Допустим, Солнце обладает такой же светимостью, что и другая звезда, чья поверхностная температура – 2000 К. Какова температура Солнца? В данном примере давайте округлим ее до 6000 К. Температура другой звезды всего 2000 К, то есть она гораздо прохладнее и не может излучать столько же энергии на единицу площади в единицу времени, сколько Солнце, но я заявляю, что светимость у этой звезды точно как у Солнца. Как такое может быть? Беру вторую звезду, вырезаю с нее лоскут площадью 1 см², с температурой 2000 К, затем вырезаю с Солнца такой же лоскут площадью 1 см², с температурой 6000 К – втрое жарче. Сколько энергии в единицу времени будет излучать такой лоскут на Солнце по сравнению с лоскутом такой же площади на звезде с температурой 2000 К? В 81 раз больше энергии. Каким же образом вторая звезда может излучать в секунду такую же суммарную энергию, как и Солнце? Если у этих звезд одинаковая светимость, то они должны отличаться чем-то еще, кроме температуры. Дело в том, что вторая звезда, сравнительно холодная, должна иметь гораздо более обширную поверхностную площадь, с которой льется излучение. Фактически ее поверхностная площадь должна быть в 81 раз больше, чем у Солнца. Это должен быть красный гигант, который за счет огромной поверхностной площади восполняет дефицит температуры. Теперь вернемся к нашим уравнениям. Чему равна площадь поверхности сферы? Она равна 4?r², где r – радиус сферы. Возможно, вы изучали это уравнение в средней школе. Дальше начинается самое интересное. Если светимость – это энергия, излучаемая в единицу времени, а энергия, излучаемая в единицу времени на единицу площади, равна ?T⁴, то мы получили уравнение, позволяющее вычислить светимость Солнца:

L_Солн = ?T_Солн⁴ ? (4?r_Солн²).

Можно составить схожее уравнение и для другой звезды. Обозначим ее светимость звездочкой, L_*. В таком случае уравнение для вычисления светимости этой звезды – L_* = ?T_*⁴ ? (4?r_*²). Теперь у меня есть уравнения для обеих. Более того, я постулировал, что L_Солн равна L_*. Я привел именно такой пример, чтобы подчеркнуть, что мне даже не требуется знать поверхностную площадь Солнца – в данной задаче речь идет лишь о соотношениях величин. Можно удивительно много узнать о Вселенной, просто присмотревшись к соотношениям.

Давайте разделим два уравнения: L_Солн/L_* = ?T_Солн⁴ ? (4?r_Солн²)/ ?T_*⁴ ? (4?r_*²). Что дальше? Я сокращу равные множители в числителе и знаменателе дроби в правой части уравнения. Первым делом сокращу постоянную. Меня не интересует ее конкретное значение, поскольку мы сравниваем два объекта и эта константа присутствует в характеристиках обеих звезд. Поэтому ее можно сократить. Кроме того, сокращается число 4 и число ?. Переходим в левую часть уравнения: что такое L_Солн/L_*? Это выражение равно 1, поскольку, как было заявлено, две звезды обладают одинаковой светимостью и их соотношение равно 1. Итак, остается значительно более простое уравнение: 1 = T_Солн⁴ ? r_Солн²/T_*⁴ ? r_*². Температура Солнца равна 6000 К, а температура другой звезды – 2000 К. Естественно, 6000⁴, деленное на 2000⁴, равно 3⁴, то есть 81. Получается, 1 = 81r_Солн²/r_*². Умножим обе части уравнения на r_*². Имеем r_*² = 81r_Солн². Извлечем квадратный корень из обеих частей уравнения, получится r_* = 9r_Солн. Радиус более холодной звезды в 9 раз больше, чем у Солнца! Это ответ. Если переосмыслить его в терминах площади, то поверхностная площадь у этой звезды должна быть в 81 раз больше солнечной, а радиус – в 9 раз больше солнечного. Члены в уравнении остаются прежними, но мы подставляем разные переменные в разные части уравнения. Вот и все, чем мы здесь занимались.

Как вы помните (из главы 2), самое жаркое время суток наступает не в полдень, а несколько позже, так как земля поглощает видимый свет. Видимый свет постепенно разогревает грунт, после чего грунт начинает испускать инфракрасное излучение. Грунт ведет себя как черное тело – впитывает солнечную энергию, а затем переизлучает ее согласно функции Планка. Температура грунта – примерно 300 К (то есть 273 К + температура грунта по Цельсию, примерно 27 °C, получается ровное значение 300 К).

Возможен вопрос: а какова светимость нашего тела? Подставим в выражение температуру тела в кельвинах, 310 К, возведем ее в четвертую степень, умножим на постоянную сигма – и узнаем, сколько энергии мы излучаем в единицу времени на единицу площади. Если подставить в формулу общую площадь вашей кожи (у взрослого человека – в среднем 1,75 м²), то получится ваша светимость, ваша мощность в ваттах. Эта энергия излучается не в видимом диапазоне, а преимущественно в инфракрасном, но мощность в ваттах у вас определенно есть. Посчитаем. Постоянная Больцмана ? = 5,67 ? 10^–8 ватт на квадратный метр, если измерять температуру в кельвинах. Умножим на (310)⁴. 310⁴ равно 9,24 ? 10⁹. Умножим это значение на 5,67 ? 10^–8 и получим 523 ватта на квадратный метр. Умножим это значение на 1,75 м² и получим 916 ватт. Это много. Однако учтите, что если вы сидите в комнате при температуре 300 К (27 °C), то по той же формуле ваша кожа поглощает 803 ватта энергии. На поддержание температуры тела уходит около 100 ватт. Эту энергию мы получаем при приеме и переваривании пищи. Теплокровные животные, чья температура тела выше температуры окружающей среды, должны есть больше, чем холоднокровные. Включая в комнате кондиционер, нужно задать два основных вопроса: 1) насколько велика комната и 2) какие еще источники энергии есть в комнате? В частности, нас интересует, сколько в комнате горит лампочек и сколько в ней находится человек, так как человека можно сравнить с лампочкой – он тоже имеет мощность в ваттах, выделяет тепло, и это также нужно учитывать при охлаждении. Чтобы определить настройки кондиционера для поддержания нужной температуры в комнате, нужно учесть, сколько человек (в ваттах) в ней соберется.

Перейду к следующему феномену под названием яркостью[5]. Наблюдаемая яркость звезды – это ее энергия на единицу площади в единицу времени, фиксируемая вашим телескопом. Яркость говорит о том, насколько яркой звезда вам кажется. Это зависит от светимости звезды, а также от того, на каком расстоянии от вас она находится. Давайте попытаемся интуитивно осмыслить яркость. Насколько ярким должен вам показаться объект? Логично, что если вы наблюдаете объект с постоянной яркостью, а потом я отодвину этот объект подальше, его яркость снизится. В свою очередь, светимость – это энергия, излучаемая объектом в единицу времени. Она никак не зависит от расстояния до вас, это просто излучаемая энергия. Она никак не зависит от измерений. Светимость 100-ваттной лампочки равна 100 ватт независимо от того, в какой точке Вселенной ее подвесить. Однако яркость зависит от расстояния между объектом и наблюдателем.

Яркость – простая штука, мне она нравится. Хотите расскажу? Опишу устройство, которое сам я не собирал, но вы можете запатентовать, если желаете. Это устройство называется масломет: заряжается куском масла. Спереди у него такой носик, откуда разбрызгивается масло (см. рис. 5.2).

Расположим ломтик хлеба в 30 см от масломета. Я откалибровал орудие так, чтобы порция масла полностью, до краешков, покрывала ломтик, расположенный на расстоянии 30 см. Если вам нравится намазывать масло на хлеб до самого края, то вы оцените такое изобретение. Теперь допустим, что я хочу сэкономить деньги, как любой хороший бизнесмен: хочу замазать тем же количеством масла несколько ломтиков хлеба. Но масло все равно должно распределяться по ломтику равномерно. Первый ломтик мы отставляли на 30 см, а эти отставим на 60 см. Масляный аэрозоль разлетится на большую площадь. На двойном расстоянии один залп поможет замаслить площадь в 2 ломтика шириной и 2 ломтика высотой. То есть масляный аэрозоль накроет решетку размером 2 ? 2 хлебных ломтика, всего намажет 4 ломтика. Всего лишь удвоили расстояние – и уже смогли намазать маслом 4 ломтика. Если утроить расстояние, то можно побиться о заклад, что аэрозоля хватит, чтобы намазать 3 ? 3 = 9 ломтиков хлеба. Один ломтик, четыре ломтика, девять ломтиков. Сколько масла попадает на один ломтик хлеба, расположенный на расстоянии 90 см, по сравнению с ломтиком, который был удален всего на 30 см? Одна девятая. Хлеб все равно орошается маслом, но вдевятеро слабее. Клиент будет недоволен, зато понятно, к чему я клоню.

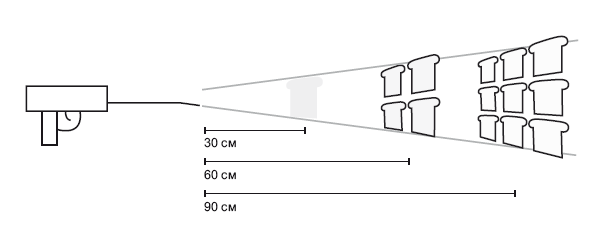
Рис. 5.2. Масломет. Он может размазать порцию масла по одному ломтику хлеба, удаленному на расстояние 30 см, по четырем ломтикам хлеба, удаленным на 60 см, или по девяти ломтикам, удаленным на 90 см. Предоставлено Дж. Ричардом Готтом

Я хочу показать, что в работе такого масломета заложен важный закон природы. Если бы вместо масла у нас был свет, то его интенсивность уменьшалась бы ровно такими же темпами, что и количество масла на один ломтик. В конце концов, свет летит по прямой линии, как и капельки масляного аэрозоля, и распределяется по тому же принципу. На расстоянии 60 см интенсивность света 100-ваттной лампочки будет составлять всего 1/4 от ее же интенсивности на расстоянии 30 см. На расстоянии 90 см останется всего 1/9 интенсивности, на расстоянии 120 см – 1/16 интенсивности, на расстоянии 150 см – 1/25 интенсивности и так далее. Интенсивность падает пропорционально квадрату расстояния – обратно квадрату. На самом деле, мы только что вывели важный физический закон, описывающий, как с увеличением расстояния ослабевает интенсивность излучения, закон обратных квадратов. Помните ньютоновскую формулу Gm_amb/r²? «Эр в квадрате» в знаменателе демонстрирует отношение по закону обратных квадратов, принцип тот же, что и в масломете. Гравитация и масломет обладают схожими свойствами.

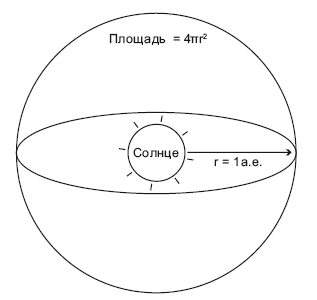
Рис. 5.3. Солнце – это сфера. Солнечное излучение распределяется по площади 4?r², перед этим проходя через сферу радиусом r. Предоставлено Дж. Ричардом Готтом

Представьте себе источник света, подобный Солнцу, излучающий во всех направлениях (рис. 5.3). Далее предположим, что я заключу Солнце в огромную сферу, равную по радиусу земной орбите (1 а.е.). Солнце излучает свет во всех направлениях, и часть светового потока я перекрываю. Я получаю лишь ничтожную долю того света, что проходит через сферу, в центре которой находится Солнце, причем радиус этой сферы равен расстоянию от Солнца до меня. Чему равна площадь этой большой сферы? Она равна 4?r², где r – радиус сферы. Из всего солнечного света та доля, что попадает в мой детектор, равна площади детектора, деленной на площадь этой огромной сферы (4?r²). Если я отодвинусь на вдвое большее расстояние, то размер моего детектора не уменьшится, а радиус сферы увеличится вдвое (2 а.е.) и площадь, через которую будут проникать лучи Солнца, станет вчетверо больше. В мой детектор попадет лишь четверть фотонов от того количества, что мне удавалось поймать, когда я был на расстоянии 1 а.е. от Солнца. Яркость выражается в ваттах на квдратный метр, улавливаемых моим детектором. Чтобы вычислить яркость, которую я буду наблюдать в радиусе r от Солнца, я беру светимость Солнца (в ваттах) и делю ее на площадь сферы – 4?r². Таким образом я узнаю, сколько ватт от Солнца получаю в пересчете «количество ватт на квадратный метр». Умножаю это значение на площадь моего детектора (скажем, телескопа) и узнаю, сколько энергии в секунду он получает. Если L – светимость Солнца, то яркость Солнца (B), которую я буду наблюдать, вычисляется по формуле B = L/4?r², где r – расстояние от Солнца до меня. По мере увеличения этого расстояния знаменатель (4?r²) растет, и яркость снижается. На Нептуне, который расположен в 30 раз дальше от Солнца, чем Земля, Солнце кажется в 900 раз тусклее, чем у нас.

Допустим, две звезды на небе обладают одинаковой яркостью, но я знаю, что светимость у одной из них в 10 000 раз выше, чем у другой. Что можно сказать об этих звездах? Звезда с большей светимостью должна находиться дальше. Во сколько раз? В 100 раз. Как у меня получилось 100? Да, 100 в квадрате равно 10 000.

Вы только что изучили некоторые из глубочайших проблем астрофизики конца XIX – начала XX века. Так, Больцман и Планк стали героями науки, поскольку осознали материал, изложенный в двух предыдущих главах.