Книга: Большое космическое путешествие

Глава 4 Как звезды излучают энергию (I)

Глава 4

Как звезды излучают энергию (I)

Автор: Нил Деграсс Тайсон

Теперь давайте попытаемся осмыслить расстояния до звезд. Как мы уже знаем, расстояние от Земли до Солнца, равное 150 миллионам километров (или 1 а.е.), примерно в 100 раз превышает диаметр самого Солнца. Если уменьшить расстояние от Земли до Солнца до одного метра, то поперечник Солнца составит 1 сантиметр. Ближайшие звезды удалены от нас примерно на 200 000 а.е., поэтому, при описываемом уменьшении, они окажутся в 200 километрах. Межзвездное пространство несравнимо объемнее самих звезд. Такие расстояния удобно пересчитывать не в километрах или сантиметрах, а с учетом времени, за которое их преодолевает свет.

Скорость света, обозначаемая буквой c, равна 3 ? 10⁸ метров в секунду – еще одно число, которое стоит запомнить. В главе 17 мы подробно рассмотрим, почему эта скорость является абсолютно предельной. Ничто не может двигаться быстрее света. Поскольку мы отслеживаем звезды именно по их свету, кажется естественным измерять расстояние именно в таких единицах. Одна световая секунда – это расстояние, преодолеваемое лучом света за секунду, то есть 3 ? 10⁸ метров, или 300 000 километров, – примерно всемеро больше земного экватора. Луна удалена от нас на 384 000 километров, свет проходит это расстояние за 1,3 секунды. Можно сказать, что расстояние до Луны – 1,3 световой секунды. Расстояние от Земли до Солнца (1 а.е.) равно примерно 8 световым минутам; свет преодолевает его за 8 минут. Ближайшие звезды расположены в 4 световых годах от нас. Итак, световой год – это не мера времени, а мера длины: он равен расстоянию, которое свет преодолевает за год. Один световой год равен примерно 10 триллионам километров. Свет ближайших звезд, который мы видим сегодня, покинул их 4 года назад. Во Вселенной мы постоянно смотрим в прошлое. Эти ближайшие звезды мы видим не такими, каковы они сейчас, а такими, каковы они были 4 года назад.

Нечто подобное наблюдается и в повседневной жизни. Можно сказать, что скорость света равна примерно 30 сантиметрам в наносекунду, поэтому два человека, сидящих по разные стороны стола, видят друг друга с запаздыванием в пару наносекунд. Разумеется, такой крошечной погрешности мы просто не замечаем, но такое запаздывание неотделимо от зрительного контакта.

Как измерить расстояние до ближайших звезд? Четыре световых года – это чрезвычайно много. Нам просто не хватит никакой рулетки, чтобы дотянуться до звезды. Поэтому давайте рассмотрим, что такое параллакс. Земля вращается вокруг Солнца (рис. 4.1). В январе Земля находится по одну сторону от Солнца, а полгода спустя, в июле, – по другую. Справа от Земли, в центре рисунка, изображена звезда, расположенная относительно недалеко, а еще правее показаны далекие звезды. Они настолько отдалены от нас, что я просто поставлю их на край страницы в линию. Теперь допустим, что я сфотографировал близлежащую звезду 1 января. В таком случае я увижу на снимке все звезды, которые были на небе, в том числе интересующую нас (на схеме она закрашена). На рис. 4.1 показано, как звездное небо выглядит с Земли 1 января. Сама по себе эта картинка, конечно, ни о чем не говорит. Помните, я не знаю, какие звезды далеко, а какие близко, – пока мне об этом ничего не известно. Но мы выждем полгода и вновь сделаем такую фотографию в июле, когда Земля будет на противоположной стороне орбиты, в совершенно новой точке. Теперь мы увидим точно такой же звездный фон, но интересующая нас звезда (закрашена) словно передвинется со своего прежнего места в точку, соответствующую июльскому положению Земли. Звезда сместится. Все остальные, в принципе, останутся на своих местах. Что произойдет за следующие 6 месяцев? Она вернется на прежнее место, туда, где была в январе. Звезда так и смещается между двумя точками в зависимости от того, в какой день года мы ее наблюдаем.

Промотайте две фотографии одну за другой, как в мультфильме, вперед, потом назад. Если при этом обе фотографии идентичны, за исключением одной звезды, которая смещается, то именно эта звезда расположена к вам ближе всех остальных. Если бы эта звезда была еще ближе, то смещение на снимке получилось бы еще заметнее. Ближние звезды сильнее «смещаются». Я пишу это слово в кавычках, поскольку звезда, конечно, никуда не движется – это мы постоянно вращаемся вокруг Солнца; все смещение связано с изменением нашей точки обзора.

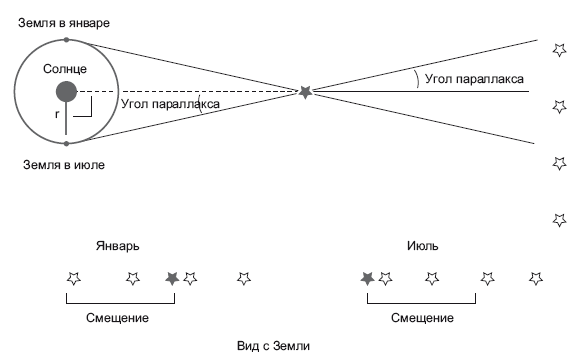
Рис. 4.1. Параллакс. Когда Земля вращается вокруг Солнца, расположенная поблизости звезда смещается на фоне более удаленных звезд. Предоставлено Дж. Ричардом Готтом

Хотите – убедитесь сами. Закройте левый глаз, вытяните руку и оттопырьте большой палец. Смотрите только правым глазом, и постарайтесь найти такой предмет, который просматривается на одной линии с большим пальцем. Затем приоткройте второй глаз. Что произойдет? Большой палец словно сдвинется. Теперь отставьте палец на половину длины руки и повторите опыт. Палец сдвинется еще значительнее. Открыв этот эффект, люди осознали, что он работает и со звездами. Ближняя звезда подобна большому пальцу, а диаметр земной орбиты – промежутку между двумя глазами. Естественно, если вы попытаетесь определить расстояние до звезды на глаз, это будет неэффективно, ведь несколько сантиметров между зрачками – слишком малое расстояние, чтобы можно было увидеть звезду под явственно разными углами. Но диаметр земной орбиты – 300 миллионов километров. Вполне достаточное расстояние, чтобы подмигнуть Вселенной и измерить, как далеко от тебя расположена та или иная звезда.

На рис. 4.2 показан подобный пример, с созвездием Лиры. Звезды на двух картинках показаны смещенными пропорционально их наблюдаемому параллаксу, как будто перед нами – два снимка, сделанных с земной орбиты с интервалом 6 месяцев. Мы немного увеличили смещение, чтобы оно было хорошо заметно.

Самая яркая звезда на снимке называется Вега, от нас до нее всего 25 световых лет. Она гораздо ближе к нам, чем соседствующие с ней звезды из центра Лиры. Если внимательно сравнить две картинки и поискать отличия, то будет заметно, что Вега сместилась сильнее других звезд.

Чем дальше звезда, тем меньше такое смещение. Но таким способом можно измерить расстояние до очень многих относительно близких звезд. Для этого придется воспользоваться простейшими геометрическими фактами.

Рис. 4.2. Параллакс Веги. Две смоделированные фотографии созвездия Лиры выглядят так, как будто они сделаны с земной орбиты с интервалом 6 месяцев, пока Земля вращается вокруг Солнца. Параллакс каждой звезды на картинках обратно пропорционален расстоянию до нее. (Смещения параллаксов значительно увеличены, чтобы они были легко заметны.) Вега (самая яркая звезда в созвездии Лира) находится на переднем плане, до нее всего 25 световых лет, она сдвигается сильнее всего. Чтобы оценить смещение параллакса Веги, достаточно сравнить ее положение на двух картинках. Эту картинку также можно смотреть в трехмерном виде – о том, как это делается, рассказано во врезке на с. 58. Постарайтесь, и увидите оба изображения как в стереоочках. Предоставлено Робертом Дж. Вандербеем и Дж. Ричардом Готтом

На рис. 4.1 мы видели, что в январе ближайшая звезда находится на фоне одной совокупности звезд, а в июле – уже на фоне другой. Половину такого смещения принято называть углом параллакса, он соответствует сдвигу, который можно было бы увидеть, если передвинуться всего на 1 а.е., а не на 2 а.е. Мы знаем, чему равен радиус земной орбиты (1 а.е.) в километрах. Можем измерить угол параллакса. Представьте себе треугольник, в вершинах которого расположены Земля, Солнце и звезда. Это будет прямоугольный треугольник, причем в вершине с углом 90° находится Солнце. Смещение угла, фиксируемое в течение года при наблюдении за близлежащей звездой, в точности соответствует тому смещению, которое заметил бы наблюдатель с той звезды, глядящий в вашу сторону. Таким образом, наблюдаемый вами угол параллакса (половина общего смещения) будет равен углу между Солнцем и Землей (в июле), который измерил бы наблюдатель с близлежащей звезды (вновь см. рис. 4.1). Следовательно, построенный нами треугольник имеет угол в 90° у вершины с Солнцем, угол, равный углу параллакса, у вершины с близлежащей звездой, а угол у вершины с Землей равен 90° минус угол параллакса. Это так, поскольку, согласно евклидовой геометрии, сумма углов треугольника равна 180°.

Нам известна длина одного из катетов треугольника (расстояние от Солнца до Земли), и если знать градусные меры всех углов треугольника, то можно измерить и длину катета, соединяющего Солнце и близлежащую звезду. Таким образом мы напрямую измеряем расстояние до звезды. Теперь давайте изобретем новую меру расстояния. Возьмем в качестве данной меры такое расстояние, чтобы удаленная на это расстояние звезда имела параллакс в одну угловую секунду. Естественно, 1 угловая секунда равна 1/60 угловой минуты, а угловая минута равна 1/60 градуса. Таким образом, угловая секунда равна 1/3600 градуса. Известно, каково может быть расстояние до звезды, параллакс которой составляет 1 угловую секунду. Такое расстояние называется 1 парсек. Нравится такое название? Угол параллакса в 1 угловую секунду равен 1/(360 ? 60 ? 60) полной окружности. Если звезда расположена на расстоянии d, то длина такой окружности будет равна C = 2?d. Отрезок между Землей и Солнцем r = 1 а.е. противолежит 1/(360 ? 60 ? 60) данной окружности, таким образом, 1 а.е./2?d = 1/(360 ? 60 ? 60). Следовательно, для параллакса в 1 угловую секунду d = 206 265 а.е. = = 1 парсек. Все это – просто евклидова геометрия.

В сериале «Звездный путь» эта единица длины используется довольно часто. Сколько это в световых годах? 3,26 светового года. Парсек – классная и интересная единица, но в этой книге мы будем оперировать прежде всего световыми годами. Если вам когда-нибудь встретится термин «парсек», то знайте его этимологию. Астрономы составили это слово из фрагментов двух других терминов: «параллакс» и «угловая секунда». Звезда с параллаксом 1/2 угловой секунды удалена от нас на 2 парсека, звезда с параллаксом 1/10 угловой секунды – на 10 парсеков. Все просто. В астрономии встречаются некоторые очень емкие термины, например «квазар». Дословно он означает «квазизвездный радиоисточник». «Пульсар» – это пульсирующая звезда. Мы придумали, а людям нравится. Есть часы Pulsar.

Какая звезда самая близкая к Земле? Это Солнце. Если вы ответили «альфа Центавра» – значит, я вас провел. Альфа Центавра – это ближайшая к Солнцу звездная система. Альфа – это самая яркая звезда конкретного созвездия, в данном случае речь идет о созвездии Центавр, что на Южном полушарии неба. На самом деле, альфа Центавра – это система из трех звезд, и одна из этих звезд расположена ближе всего к Солнцу. Тройная звездная система – это очень круто. В нее входят альфа Центавра А, звезда, схожая по типу с Солнцем, ее диаметр – 123 % солнечного; альфа Центавра B, ее диаметр – 86,5 % солнечного, и Проксима Центавра – тусклая красная звезда, диаметр которой – всего 14 % солнечного. Из трех этих звезд ближе всего к Солнцу расположена Проксима Центавра. Поэтому она и называется «Проксима» – в переводе с латыни «ближайшая». До нее примерно 4,1 светового года, ее параллакс – 0,8 угловой секунды.

Одна угловая секунда – это очень, очень мало. Вспомните практически любую фотографию ночного неба, которую вам доводилось видеть, сделанную с Земли при помощи профессионального телескопа, – видимый размер звезды на таком снимке обычно составляет около одной угловой секунды. Это типичный показатель для наземных телескопов. Качество фотографий с космического телескопа «Хаббл» в десять раз лучше. Когда мы работаем с наземными телескопами, нам страшно мешает атмосфера, из-за которой все звезды выглядят размытыми. Звездный свет прилетает к нам в виде идеально очерченной точки, строго следуя выбранному курсу. Затем он врезается в атмосферу, рассеивается, переливается и размазывается – вот и получается такое пятнышко. Мы на Земле говорим: «Как красиво! Звездочка мерцает». Но мерцание – просто погибель для астронома, рассматривающего звезду, а типичная ширина такого мерцания – 1 угловая секунда.

Обратите внимание: расстояние в 1 парсек меньше, чем до ближайшей звезды. Вот почему прошли тысячи лет, прежде чем удалось измерить параллакс. Первый звездный параллакс лишь в 1838 году измерил немецкий математик Фридрих Бессель. (Если атмосфера искажает звезду более чем на 1 угловую секунду в ширину, то астроном должен сделать при помощи телескопа множество замеров, чтобы достичь точности выше 1 угловой секунды.) На самом деле аргументы в пользу вращения Земли вокруг Солнца, выдвинутые Аристархом более 2000 лет назад, опровергались именно потому, что в те времена не удавалось наблюдать параллакс. Древние греки были смышленые ребята. «Ладно, – говорили они, – вам не нравится наша геоцентрическая Вселенная, где Солнце вращается вокруг Земли?» Они знали, что если бы Земля действительно вращалась вокруг Солнца, то ближайшие звезды просматривались бы под разными углами, в зависимости от того, с какой стороны от Солнца находится Земля. То есть они считали, что мы должны были бы замечать такой эффект параллакса. До изобретения телескопа было еще далеко, поэтому они просто внимательно смотрели на небо и продолжали смотреть. Как бы внимательно они ни вглядывались, ровно никакой разницы они заметить не могли. На самом деле, поскольку такой эффект невозможно измерить без телескопа, отсутствие параллакса использовалось в качестве мощного аргумента против гелиоцентрической Вселенной. Но отсутствие доказательств далеко не всегда равноценно доказательству отсутствия.

Даже рассмотрев все эти звезды в ночном небе и заметив, что среди них попадаются размытые объекты, напоминающие облака тумана, мы еще не вполне представляли себе Вселенную вплоть до начала XX века. К тому времени звездный свет уже пропустили через призму, разложили и посмотрели, какими характеристиками он обладает. Тогда стало известно, что некоторые звезды можно использовать в качестве «эталонных источников света». Давайте об этом подумаем. Если бы все звезды в небе были совершенно одинаковы – например, нарезаны формочкой для печенья и заброшены на небо, – то сравнительно тусклые обязательно находились бы дальше сравнительно ярких. Все было бы просто. Все яркие звезды – близко. Все тусклые звезды – далеко. Но на деле все иначе. Среди всего этого звездного многообразия, независимо от того, где какие звезды расположены, мы ищем и находим звезды одной и той же категории. Итак, если найдется звезда, для спектра которой характерна какая-то специфическая особенность, и эта звезда находится достаточно близко, чтобы можно было измерить ее параллакс, – нам повезло. Теперь мы можем взять ее светимость в качестве отсчетной и определить яркость других подобных ей звезд как «вчетверо меньше» или «вдевятеро меньше», а затем вычислить, как далеко они находятся. Но сперва надо найти такой эталонный источник, мерило. Вплоть до 1920-х годов таких мерил не было. До тех пор мы совершенно не представляли, насколько удалены от нас те или иные тела во Вселенной. На самом деле, в книгах того времени Вселенная описывается просто как «область, заполненная звездами», о более крупной Вселенной за пределами этой области ничего не было известно.

Когда пытаешься понять звезды, непременно нужны дополнительные математические инструменты. Один из них – функции распределения. В них заложены мощные и полезные математические идеи. Я хотел бы рассказать о них на простом примере, поэтому давайте начнем с так называемой гистограммы. Например, на такой диаграмме можно распределить количество человек в типичной аудитории американского колледжа в зависимости от их возраста (рис. 4.3).

Чтобы построить такой график, нужно спросить присутствующих, есть ли в аудитории кто-либо в возрасте 16 лет или моложе. Если никто не отзовется, то на графике этим возрастам будут соответствовать нулевые значения. Далее спросим, сколько 17–18-летних. Допустим, наберется 20 человек. Отметим этот возраст планкой, высота которой – ровно 20 единиц. А сколько тех, кому 19–20 лет? Тридцать пять человек. Так и продолжим, пока не учтем всех присутствующих.

Теперь давайте вернемся к рис. 4.3. Гистограмма позволяет кое-что сказать о распределении слушателей по возрасту в типичной аудитории. Например, большинству из них около 20 лет – из графика сразу ясно, что речь идет о группе из колледжа. Затем следует пробел, несколько одиночных значений и еще один всплеск, в районе 75 лет. На этом графике два всплеска, они называются модами. Такое распределение называется бимодальным. Большинство представителей «старшей» группы – никакие не студенты; вероятно, это вольнослушатели. Если человек может в дневное время посещать лекции в колледже, это значит, что он не обязан работать с девяти до шести, то есть это пенсионер. Можно представить себе демографическую картину, просто взглянув на такое распределение. Если бы мы построили такую гистограмму сразу для всего колледжа, то, вероятно, некоторые пробелы заполнились бы, но я готов поспорить, что общая картина осталась бы почти такой же: в основном младшие студенты, небольшое количество пожилых. Чисто случайно могут попадаться подростки-вундеркинды – может быть, один на тысячу, – поскольку, кажется, на каждом новом потоке хоть один да попадется. На такой гистограмме картинка будет повторяться с интервалом в 2 года. Думаю, если бы удалось достаточно увеличить размер выборки и включить в график всех студентов колледжей в США, интервал удалось бы уменьшить до 1 дня. Я мог бы собрать такое количество данных, что столбики на диаграмме вообще перестали бы просматриваться. При таком объеме данных интервалы на диаграмме стали бы слишком узки, и мне пришлось бы перерисовать эту диаграмму в виде сплошной кривой. Если вы переходите от гистограммы к плавной кривой и можете представить ее в математической форме, то гистограмма превращается в функцию распределения.

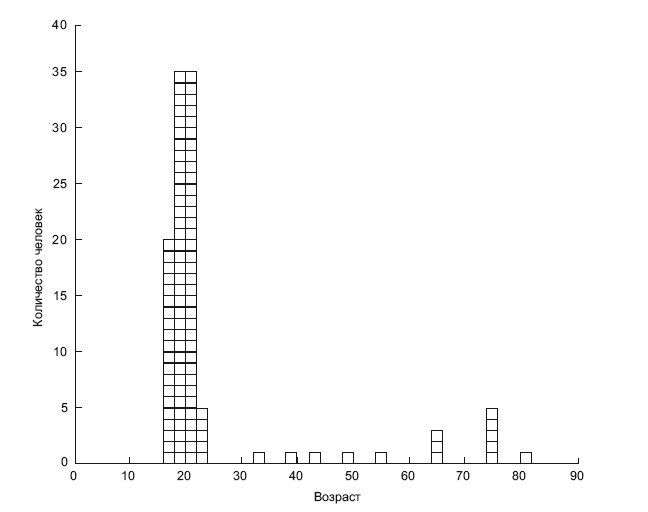
Рис. 4.3. Гистограмма, демонстрирующая распределение слушателей в аудитории по возрасту. Предоставлено Дж. Ричардом Готтом

Сколько всего человек в этой группе? Это легко узнать – идем по шкале слева направо и складываем цифры. В данном случае получается 109. При работе с гладкими функциями можно пользоваться интегральным исчислением, суммировать площадь под кривой и узнавать, сколько всего элементов на ней представлено. Исаак Ньютон изобрел интегральное исчисление в возрасте 26 лет, – я считаю, он вообще был умнейшим человеком, когда-либо жившим на Земле!

Какое отношение все это имеет к звездам? Возьмем, к примеру, Солнце. Я скажу ему: «Солнце, поведай мне, сколько частиц света ты излучаешь?» Еще я мог бы добавить, что Исаак Ньютон задолго до Эйнштейна высказал идею, что свет состоит из частиц (корпускул). Эти частицы называются «фотоны» – не протоны, а именно фотоны. Корень «фото» тот же самый, что и в слове «фотография», еще можно вспомнить «фотонные торпеды», – фанаты сериала «Звездный путь» знают, что это такое.

Фотоны бывают самыми разными. Исаак Ньютон пропустил белый свет через призму и перечислил те цвета радуги, которые увидел: красный, оранжевый, желтый, зеленый, голубой, индиго (так называется синий краситель, популярный во времена Ньютона) и фиолетовый. Вы можете запомнить эту последовательность с помощью мнемонической фразы для запоминания цветов радуги: «Каждый охотник желает знать, где сидит фазан».

Английский астроном Уильям Гершель открыл совершенно иную часть спектра, которая сегодня называется инфракрасным излучением. Человеческий глаз его не воспринимает. С энергетической точки зрения он находится «ниже» красного. Гершель пропускал солнечный свет через призму и заметил, что термометр нагревается, если поместить его у красного конца спектра. В некоторых ресторанах используются инфракрасные лампы; под ними держат картофель-фри, поэтому гость всегда получает его теплым. Можно выйти за пределы видимого спектра и с другой стороны, тогда мы попадем в область ультрафиолетового (УФ) излучения. Об этих областях спектра вы слышали ранее, поскольку они упоминаются повсюду. Ультрафиолетовое излучение – причина загара и солнечных ожогов.

Таким образом, спектр гораздо шире видимой части. За ультрафиолетовым спектром расположен рентгеновский. В нем – свои фотоны. За рентгеновским – гамма-излучение. Об этих частях спектра вы тоже слышали. Отправимся в противоположную часть спектра – за инфракрасный. Что там? Микроволны. А за ними? Радиоволны. Раньше микроволны считались подмножеством радиоволн, но теперь классифицируются как самостоятельная часть спектра. Вот и все области спектра, для которых есть названия. За гамма-излучением ничего нет, только гамма-излучение, и за радиоволнами тоже ничего нет, только радиоволны.

Фотон – это частица. Но его можно трактовать как волну, это свойство называется «корпускулярно-волновой дуализм». Что же это значит, спросите вы, фотон – это волна или частица? Этот вопрос не имеет смысла. Скорее можно спросить о том, почему наш мозг не может изловчиться и представить себе объект, которому присуща такая двойственная природа. Это проблема. Можно изобрести новое слово, например «волница». Такой термин уже предлагали, но он так и не прижился, поскольку вопрос «что это такое?» по-прежнему актуален. Все зависит от того, как измерять свет. Можно считать его волной, а у волны есть длина. Длина волны обозначается греческой буквой «лямбда». Мы пользуемся строчной буквой, именно ею обычно обозначается длина волны.

Какова длина радиоволны? Представьте себе: давным-давно, если вы хотели переключить телевизионный канал, нужно было встать с дивана, подойти к телевизору и повернуть ручку. Да, были времена. На таких телевизорах стояла «рогатая» антенна – с двумя телескопическими уловителями, которые выдвигались из нее в форме буквы V. Если сигнал был плохой, нужно было потрогать эти рога. Они имели строго определенную длину, около метра. На самом деле, длина волн, обеспечивающих телесигнал, – тоже около метра. Антенна принимала телевизионные волны прямо из воздуха. Да, сегодня телесигнал обычно идет по кабелю, но вообще любые фотоны (в том числе радиоволны) совершенно свободно распространяются и в вакууме.

Поговорим о сотовых телефонах. У них большие антенны? Нет, совсем маленькие. Они работают в диапазоне микроволн, длина которых – около сантиметра. Сегодня антенну встраивают в сам телефон, но раньше, если вы собирались позвонить по сотовому, из него нужно было выдвинуть короткую толстую антенну.

Какой величины отверстия в переднем щитке вашей микроволновки? Да, там есть отверстия, поэтому вы и видите пищу, подогреваемую внутри. Может быть, вы и не обращали внимания, но они совсем маленькие – всего пара миллиметров в диаметре, гораздо меньше тех самых микроволн, что разогревают вам еду. Поэтому микроволны просто не могут вырваться из печки наружу. А знаете, где еще используются микроволны? В полицейских радарах, при помощи которых отслеживается превышение скорости. Микроволны отражаются от металлического корпуса автомобиля. Есть способ от них защититься: знаете такие плотные черные чехлы от насекомых («мухобойки»), которые любят надевать на передок своих машин некоторые водители, обычно владельцы спортивных автомобилей? Такой чехол отлично поглощает микроволны, поэтому если он попадет под радар, то сигнал получится настолько слабым, что полиция его просто не заметит. Естественно, автомобильное ветровое стекло прозрачно для микроволн. Откуда известно, что микроволны свободно сквозь него проникают? А где водитель ставит антирадар? Обычно – в салоне машины, прямо на приборном щитке. Итак, очевидно, что микроволны проникают сквозь стекло. Именно поэтому вполне можно готовить в микроволновке блюда в стеклянной посуде – стекло прозрачно для микроволн. Полиция, фиксируя вашу скорость, пользуется так называемым доплеровским смещением, это явление мы обсудим чуть ниже. Пока сформулируем так: в данном случае доплеровское смещение – это степень изменения длины волны при отражении сигнала от движущегося тела. Смещение можно измерить максимально точно, если измерительное устройство расположено прямо на пути движущегося объекта. На практике радар измеряет скорость машины лишь приблизительно – чтобы измерить ее точно, полицейский должен был бы стоять прямо посреди трассы, а они так обычно не делают. Они стоят на обочине, поэтому (к сожалению) их радары всегда фиксируют заниженную скорость. Поэтому если вас остановят за превышение, то вам нечем крыть. Платите штраф и поезжайте дальше.

Полицейский радар испускает сигнал, отражающийся от автомобиля. Допустим, вы взглянули на собственное отражение в зеркале. В этот момент зеркало находилось в 3 метрах от вас, но оно движется в вашу сторону со скоростью 30 сантиметров в секунду. Ваше отражение появляется в 6 метрах от вас (свет успевает пройти 3 метра от вас до зеркала, а потом – 3 метра от зеркала до вас). Но всего через секунду зеркало уже на 30 сантиметров ближе к вам, и вы видите свое отражение на расстоянии всего 5,5 метра. Ваше отражение мчится к вам со скоростью 60 сантиметров в секунду. Аналогично, полицейский, который фиксирует у себя на радаре скорость вашего автомобиля, получает показатель, вдвое превышающий вашу скорость. Попробуйте объяснить это судье! Разумеется, радары откалиброваны так, что показывают вдвое уменьшенный показатель доплеровского смещения и, соответственно, точную скорость «зеркала» – вашего автомобиля. Кстати, слово «радар» в английском языке – это аббревиатура, означающая «радиообнаружение и измерение дальности», ведь радары появились еще в те времена, когда микроволны считались подмножеством радиоволн.

Поскольку мы говорим о микроволнах, упомяну, что молекула воды H₂O очень к ним чувствительна; волны в вашей микроволновой печи переворачивают эту молекулу с частотой самой волны. Если у нас есть капелька воды, то это будет происходить со всеми молекулами в ней. С миллиардами триллионов молекул. Вскоре вода нагреется – из-за трения, возникающего между этими молекулами. Также нагреются любые попадающие в микроволновку продукты, в которых есть вода. Все, что мы едим (кроме соли), содержит воду. Вот почему в микроволновке так удобно разогревать и готовить, и по этой же причине она не нагревает стеклянные тарелки, на которых нет еды.

Человеческое тело реагирует на инфракрасное излучение. Кожа поглощает его, преобразует в тепло, и мы это чувствуем. Видимый свет нам хорошо известен. Люди с разным цветом кожи обладают разной восприимчивостью к ультрафиолету. Ультрафиолет может повредить глубокие слои кожи и вызвать рак. Атмосферный озон поглощает большую часть солнечного ультрафиолета. В атмосфере содержится обычный молекулярный кислород (O₂) плюс небольшое количество озона (O₃) – это молекулы, состоящие из двух и трех атомов кислорода соответственно. Озон находится в верхних слоях атмосферы, он постоянно «готов к распаду». Прилетает фотон ультрафиолета, молекула озона «впитывает» его и распадается. Ультрафиолета не осталось – озон просто поглотил его. Если убрать озон, то солнечный ультрафиолет будет беспрепятственно достигать поверхности Земли, и заболеваемость раком кожи резко повысится. На Марсе нет озона, и его поверхность постоянно купается в потоках солнечного ультрафиолета. Именно поэтому мы полагаем (и, думаю, не ошибаемся), что на поверхности Марса нет никакой жизни, хотя под поверхностью она и может существовать. Любой биоматериал, подвергшийся такому ультрафиолетовому воздействию, быстро бы разложился.

Практически каждый из нас подвергался рентгеновскому облучению. Помните, что делает рентгенолог, прежде чем сделать снимок? Он ставит вас в правильную позу, говорит «Вдохнуть – не дышать!», а затем выходит за свинцовую дверь и только после этого включает аппарат. Врач не хочет попасть под рентгеновское излучение. Логично предположить, что это вредная процедура. Но обычно рентгеновское облучение – меньшее зло, чем отказ от него. Например, оно может понадобиться для диагностики; если у вас сломана рука, то рентген это покажет. Рентгеновские лучи проникают не только под кожу, но и гораздо глубже; они могут вызывать рак внутренних органов. Но если вы получаете небольшую дозу такого излучения, то риск невелик.

Гамма-лучи еще хуже. Они бьют прямо по ДНК и могут устроить там хаос. Даже в комиксах пишут, что гамма-лучи – это плохо. Помните Невероятного Халка? Как он стал Халком? Что с ним случилось? Помните, был эксперимент, в ходе которого он получил большую дозу гамма-излучения. Теперь, когда Халк злится, он превращается в огромного уродливого зеленого монстра. Поэтому берегитесь гамма-лучей – не хотелось бы, чтобы с вами произошло нечто подобное. По мере движения в коротковолновую часть спектра – от ультрафиолетовых лучей к рентгеновским и далее к гамма-излучению – энергия каждого отдельного фотона возрастает, равно как и его вредоносность.

Сегодня нас повсюду окружают радиоволны. Постоянно. Чтобы в этом убедиться, достаточно поставить простой эксперимент. Включите радио и настройтесь на станцию. На любую, в любое время. Радиосигнал ловится везде, станции вещают круглосуточно. Как убедиться, что вокруг нас – постоянные потоки микроволн? Ваш мобильник может позвонить в любой момент, например прямо сейчас. Если вы не станете засовывать голову в мощное поле работающей микроволновой печи, то микроволны совершенно безопасны по сравнению с тем, что творится в высокоэнергетической части спектра.

Все эти фотоны перемещаются в вакууме со скоростью света. Это не просто хорошая идея, а закон. Видимый (для нас) свет находится в средней части электромагнитного спектра, но все фотоны летят со скоростью 300 тысяч километров в секунду (если быть точным – 299 792 458 метров в секунду). Это одна из наиболее важных фундаментальных констант, которые нам известны.

Скорость фотонов во всех диапазонах спектра одинакова, но длина волны у них разная. Если я встану и буду смотреть, как мимо меня пролетают электромагнитные волны, то частоту волны можно определить как количество гребней этой волны в секунду. Чем короче волна – тем больше гребней в секунду. Поэтому короткие волны обладают высокой частотой и, наоборот, длинные волны обладают низкой частотой. Отличная ситуация, чтобы вывести тождество: скорость света (c) равна частоте, умноженной на длину волны (?). Частота обозначается греческой буквой ню: ?. Получается уравнение:

c = ??.

Допустим, мы имеем дело с радиоволнами, длина которых – 1 метр. Скорость света приблизительно равна 300 000 000 метров в секунду, что равно ? раз на метр. Таким образом, частота составляет 300 000 000 гребней (или циклов) в секунду (или 300 мегациклов).

На самом деле, есть еще одно уравнение, связывающее частоту и энергию фотона. Энергия E фотона равна h:

E = h?.

Это уравнение открыл Эйнштейн. В уравнении используется постоянная Планка h, названная в честь немецкого физика Макса Планка. В этом уравнении она служит константой пропорциональности, описывая, как взаимосвязаны частота и энергия фотона. Чем выше частота – тем больше будет энергия отдельно взятого фотона. В рентгеновских фотонах содержится огромное количество энергии, а в фотонах радиоволн – малая толика.

Теперь спросим Солнце: сколько фотонов каждой конкретной частоты ты нам даешь? Сколько зеленых фотонов прилетает с твоей поверхности, сколько красных, инфракрасных, микроволновых, радиоволновых и гамма-лучевых? Хочу знать. От Солнца мы получаем столько фотонов, что можно построить гораздо более точную картину, нежели простую гистограмму, – ведь данные поступают сплошным потоком. Я могу сделать гладкую кривую, и на этом графике я отложу интенсивность как функцию длины волны. В данном случае интенсивность, обозначаемая по оси ординат, соответствует количеству фотонов, за секунду поступающих с каждого квадратного метра поверхности Солнца, на единичный интервал длин волн, умноженному на энергию, которой обладает каждый фотон. Мы могли бы просто подсчитать фотоны, но, в конечном счете, нас интересует именно энергия, которую они несут. По оси ординат можно оценить мощность (количество энергии в единицу времени), поступающую с солнечной поверхности на единицу площади на единичный интервал длин волн. По оси абсцисс откладывается длина волны, возрастающая слева направо. Итак, давайте изобразим на графике рентгеновские лучи, ультрафиолетовые лучи, видимый спектр (цвета радуги), инфракрасные волны (ИК) и микроволны (обозначим их ?-волны). На рис. 4.4 показана функция распределения интенсивности солнечного излучения.

Жаркое Солнце излучает энергию с температурой около 5800 К. Распределение было построено Максом Планком. Пиковая часть графиков приходится на видимую часть спектра, и это не случайно: наши глаза развивались таким образом, чтобы улавливать максимальное количество солнечного света. Для сравнения с другими звездами давайте выберем «средний» квадратный метр и воспользуемся им в качестве примера. Не так важно, на какой именно мере площади мы остановимся, – главное пользоваться ею во всех примерах. Иногда мы говорим, что Солнце желтое, но оно не желтое. Нам нравится называть его желтым, поскольку пик светимости лежит в районе желтого цвета, однако с тем же успехом можно считать, что пик находится в районе зеленого; но никто же не скажет, что у нас в небе – зеленая звезда. Кроме желтого в солнечном

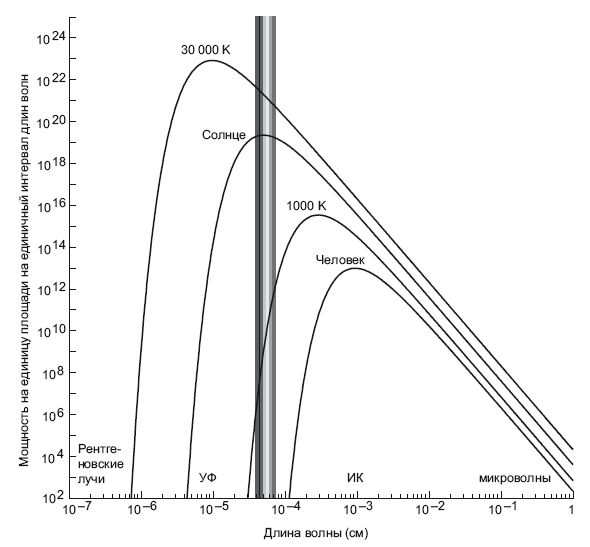
Рис. 4.4. Излучение, испускаемое звездами и людьми. По оси ординат откладывается энергия в единицу времени (то есть мощность), излучаемая различными объектами на единицу поверхностной площади на единичный интервал длин волн. По оси абсцисс откладывается длина волны. Показана звезда с температурой поверхности 30 000 К, Солнце (5800 К), коричневый карлик (1000 К) и человек (310 К). Показаны длины волн, соответствующие рентгеновским лучам, ультрафиолету, видимому свету (полоса, окрашенная в цвета радуги), инфракрасному и микроволновому диапазонам.

Предоставлено Майклом Строссом

свете необходимо в равной степени учесть фиолетовый, синий, голубой, зеленый и красный, об этом свидетельствует график. Сложите их все – и у вас получится смесь, где все эти цвета присутствуют практически в равных долях. Вспомним Исаака Ньютона. Что это за смесь? Это белый цвет. Если пропустить обратно через призму все цвета спектра в равных долях, то на выходе получим белый свет. Кстати, Ньютон ставил такой эксперимент. Неважно, каким Солнце рисуют в книгах, неважно, что говорят люди, – на практике у нас в небе светит белая звезда, вот так все просто. Кстати, если бы Солнце действительно было желтым, то в совершенно ясную погоду все белые предметы, в том числе снег, казались бы желтыми.

Температура поверхности Солнца – около 5800 К. Чтобы узнать температуру в кельвинах, нужно взять величину в градусах Цельсия (C) и прибавить к ней 273. Вода замерзает при 0 °C (или 273 К). Вода кипит при 100 °C (или 373 К). Значения по Цельсию и по Кельвину отличаются всего на 273 единицы, и чем более высокие температуры мы рассматриваем, тем менее существенной становится эта разница. В любом случае, 5800 К – очень жарко. При такой температуре вы просто испаритесь. Для полноты картины расскажу, что такое 0 К (возможно, вы слышали выражение «абсолютный ноль»). Это минимальная возможная температура. При 0 К любое движение молекул прекращается.

Рассмотрим другую звезду. Вот сравнительно «холодная», поверхностная температура которой – всего 1000 К (см. рис. 4.4). Где пик излучения такой звезды? В инфракрасном спектре. Так что, эта звезда невидима? Нет. Небольшая часть ее излучения приходится на видимый спектр. Интенсивность ее излучения в видимой части спектра стремительно падает, то есть она излучает гораздо больше красного, чем голубого. Нам такая звезда покажется красной. Теперь рассмотрим звезду с поверхностной температурой 30 000 К. Напоминаю: о распределении света я задаю тот же вопрос, что и о распределении слушателей в аудитории по возрасту. Где пик излучения этой звезды? В ультрафиолетовой области. Она излучает в ультрафиолетовой части спектра больше энергии, чем в какой-либо другой. Мы не видим ультрафиолет, но сможем ли увидеть такую звезду? Да, естественно. Она отдает огромное количество энергии и в видимой части спектра, гораздо больше, чем отдает поверхность Солнца. Но, в отличие от Солнца, смесь цветов в данном случае не равномерна, а выраженно смещена к голубой части спектра. Если сложить всю цветовую гамму такой звезды, получится голубой цвет. Любой астрофизик знает, что самый холодный свет – красный, а самый жаркий – голубой.

Пик излучения нашей звезды с поверхностной температурой 30 000 К приходится на ультрафиолетовую часть спектра. Если бы я выбрал еще более горячую звезду, она также казалась бы нам голубой. Когда мы видим голубой цвет, это означает, что рецепторы голубого на сетчатке просто получают больше энергии, чем рецепторы зеленого и красного. Звезда с поверхностной температурой 30 000 К голубая, с поверхностной температурой 5800 К – белая, а с поверхностной температурой 1000 К – красная.

Что насчет человеческого тела? Какая у вас температура? Если не повышенная, то примерно 36,6 °C, или 310 К. Пик нашего излучения приходится на инфракрасную часть спектра. Сколько видимого спектра обычно отражает человек? Мы видим других людей именно потому, что их тела отражают свет в видимом спектре. Но если выключить свет, все в комнате становится черным. На диаграмме видно, что при выключенном свете тела с температурой 310 К практически не излучают свет в видимом спектре. Но при этом они все равно излучают инфракрасный. Если вооружиться тепловизором или инфракрасными очками ночного видения, то вы легко увидите в темноте людей, которые «ярко светят» в инфракрасном спектре. В следующей главе мы изобразим на подобной диаграмме целую Вселенную.