Книга: ЧЕЛОВЕК И НООСФЕРА
Ситуация «путешественников в одной лодке»
| <<< Назад Пример простейшего кооперативного соглашения |
Вперед >>> Некоторые комментарии |
Ситуация «путешественников
в одной лодке»
Первая из таких конфликтных ситуаций была изучена моими коллегами по Вычислительному центру Академии наук СССР профессором Ю. Б. Гермейером и кандидатом физ. — мат. наук И. А. Вателем. Позднее эта ситуация вошла в литературу под названием «путешественники в одной лодке».
Ее особенность состояла в том, что все участники этой конфликтной ситуации, имея разнообразные собственные интересы, были связаны еще и одним общим интересом, общей целью (доплыть до берега). Для того чтобы достичь этой общей цели, каждый из путешественников должен был часть своих ресурсов — продовольствия, воды, физической силы, одежды, нужных ему для достижения своих собственных целей, — выделить в «общий котел». Иначе им до берега не добраться.
Математическая особенность ситуации «путешественников в одной лодке» состояла в существовании некоторой монотонной зависимости степени достижения общей цели от вкладов путешественников в «общий котел»: чем больше туда будет вложено ресурсов, тем быстрее и легче будет достигнута общая цель.
Оказалось, что к такой ситуации может быть сведено описание многих экологических проблем и они могут быть проанализированы в ее рамках. Чтобы пояснить сказанное, рассмотрим один условный пример.
Как уже говорилось, структура противоречий, которая определяет содержание большинства эволюционных процессов, протекающих в обществе, и связанная с преодолением экологических трудностей, такова, что она никогда не бывает строго антагонистична. Во всяком случае, в математическом смысле этого слова: в спектре интересов субъектов всегда есть некоторая общая составляющая. Отсюда проистекает и универсальность многих математических построений.
Надо заметить, что эта особенность свойственна и миру животных, а не только Человеку. Чисто антагонистические ситуации вовсе не являются самыми типичными. Даже в такой классической и хорошо изученной экологами ситуации, как хищник — жертва, прямого антагонизма нет: хищник без жертв погибнет — это более или менее очевидно. Но и жертвы, например копытные (олени), при отсутствии хищников (волков) более или менее быстро вырождаются. Это утверждение основывается на обширном экспериментальном материале.
В общественной жизни такое явление имеет особенно четко выраженный характер. Оно — следствие чрезвычайной сложности взаимосвязей и взаимозависимости между различными субъектами, активность которых определяет мировой процесс общественной эволюции.
Заметим, что именно сложное переплетение интересов и взаимосвязей определяет устойчивость общественных структур подобно тому, как устойчивость башни Шухова определяется не массивностью конструкции, как у башни Эйфеля, а большим количеством внутренних связей между ее элементами.
Для того чтобы объяснить те особенности, которые вносят в характер конфликтов экологические факторы, я не могу; к сожалению, ограничиться словесным пояснением и должен привести некоторые конкретные расчеты. После этих замечаний перейдем к рассмотрению нашего иллюстративного примера.
Предположим, что два независимых субъекта, которых мы обозначим через А и В, — это руководители двух заводов, расположенных на берегу одного и того же водоема, реки или озера. Я употребил термин «независимые субъекты», предполагая, что каждый из них имеет в своем распоряжении определенный ресурс (например, деньги) и может им распоряжаться по своему усмотрению. Условимся для определенности, что эти субъекты — директора заводов, принадлежащих разным фирмам, корпорациям или даже странам. Это означает, что между ними нет никаких связей иерархического характера. Но другие связи, например, обусловленные особенностями процессов производства и экологии, быть могут.
Предположим далее, что каждый из этих директоров имеет некоторые «эгоистические» цели. Условимся для определенности, что каждый из них стремится максимально увеличить прибыль собственного завода. Но для производства и жизни коллектива завода им нужна вода. Свежая, чистая вода. Одним больше, другим меньше. Но так или иначе, вода нужна каждому предприятию, и каждому из субъектов приходится отчислять часть средств из собственного бюджета на очистку водоема и строительство очистных сооружений.
Итак, каждый из субъектов находится в условиях, когда он часть собственного бюджета должен расходовать на поддержание экологического равновесия и, следовательно, делать выбор в способах распределения своего ограниченного ресурса по общим целям. Другими словами, распределение ресурса ставит перед каждым из субъектов некоторую задачу многокритериальной оптимизации: надо так распределить свой ресурс, чтобы и доход был побольше, и вода почище.
А ведь ресурс один и тот же. Да и к тому же качество воды зависит не только от действий самого субъекта, но и от его партнера. Ведь они используют воду из одного и того же источника и вместе ее очищают.
Возникает очевидная и непростая задача — создать такую систему отчислений на очистку воды, которая была бы всем этим предприятиям выгодна. В некотором смысле даже оптимальная, чтобы ни одному из предприятий было бы не выгодно отклоняться от принятых однажды договорных отношений. Заметим, что эта ситуация удовлетворяет условиям монотонности, которые использовал в своих исследованиях Ю. Б. Гермейер: чем больше каждый из партнеров выделит денег (или других ресурсов) на очистку воды, тем большей будет степень достижения их общей цели — тем чище будет вода.
Попробуем теперь эту задачу описать с помощью языка математики. Наши пояснения будут очень просты, но они позволят увидеть некоторые специфические особенности проблемы.
Итак, есть два предприятия А и В. Каждое из них располагает некоторым ресурсом. Для простоты рассуждений пусть это будут деньги. В реальной жизни бывает, конечно, сложнее — приходится учитывать многие виды ресурсов: и деньги, и рабочую силу, и технику. Но такое упрощение не меняет содержания проблемы.
Обозначим через QA и QB количество денег, которые могут потратить предприятия А и В соответственно и на совершенствование предприятий, что дает им дополнительную прибыль, и на создание коллективных очистных сооружений. Через YA и YB в обозначим те доли ресурсов, которые руководители предприятий А и В предполагают вложить в развитие своих предприятий, а через ХA и ХB — доли своих ресурсов, которые они собираются использовать на создание системы очистки воды. Предположим также, что никаких других трат у предприятий нет. Тогда очевидны следующие балансовые соотношения:
ХA + YA = QA +YB= QB.
Значит,
ХA = QA — YB; ХB = QB— YB.
Выделяя на реконструкцию или развитие предприятий сумму YA, руководство предприятия А должно знать тот эффект, который оно получит от этой деятельности, например, дополнительную прибыль. Обозначим ее через ?A(YA). ?A будет, очевидно, монотонно возрастающей функцией величины инвестиций YA: чем больше предприятие вкладывает в собственное совершенствование, тем больше должен быть эффект. Точно так же мы определим и функцию ?B(YB) — результат капиталовложений в реконструкцию предприятия В.
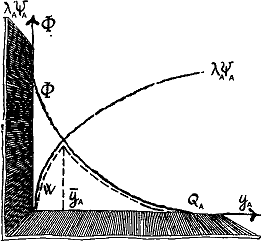
Рис.3.
Теперь о капиталовложениях в систему очистки воды. Качество воды, которое мы обозначим через ?, будет зависеть от того, какое количество денег будут вкладывать в это дело оба партнера, то есть от их общих совместных действий:
Ф = Ф(ХA, ХB) = Ф(QA — YA; QB— YB).
Эта функция будет монотонно возрастающей функцией каждой из своих переменных ХA и ХB, соответственно, монотонно убывающей функцией YA и YB.
Используя эти обозначения, интересы предприятия А мы можем записать в следующей форме:
?A(YA) ? max;
Ф(QA — YA, QB— YB) ? max.
И точно так же мы можем описать интересы и предприятия В:
?B(YB) ? max;
Ф(QA — YA, QB— YB) ? max.
Эти выражения означают, что каждое из предприятий стремится одновременно и увеличить свой доход ? и чистоту воды ?. Они это не могут делать независимо друг от друга, поскольку качество воды зависит от их совместных действий.
Обратим внимание на то, что, проведя анализ этой конфликтной ситуации, мы неизбежно должны решить одну промежуточную и очень непростую задачу. Поясним ее следующим образом.
Предположим, что предприятию А известны действия предприятия В, то есть ему известна величина QB — YB — количество ресурса, которое выделяет предприятие В на очистку воды. Тогда действия предприятия А уже могут быть полностью самостоятельными. И перед ним стоит задача: как разделить свой ресурс между двумя целями, когда результат полностью зависит только от него самого?
Оказывается, математика на этот вопрос не может дать однозначного ответа — для этого необходима некоторая дополнительная гипотеза. Поскольку непосредственной связи между доходом и чистотой воды нет, руководство предприятия должно уметь соизмерять свои интересы, знать, в каком соотношении находятся обе цели, которые преследует предприятие.
Другими словами, оно должно уметь назначить некий коэффициент ?A, соизмеряющий критерии ?A и ?. Теперь мы эти критерии будем записывать как Ф и ?A ?A и полагать, что ? и ?A ?A имеют по величине один порядок. Это означает, что чем меньше ?A, тем большее значение субъект А придает своему внутреннему «эгоистическому» критерию, то есть доходу, и тем меньшее значение для него играет качество воды ?.
Если руководство предприятия не может соизмерить или сопоставить важность обоих показателей, то это означает одно из двух: либо ему безразличны величины этих показателей (они не отражают его интересов), либо это руководство некомпетентно, недостаточно хорошо знает нужды руководимого им предприятия или коллектива. В обоих случаях такое руководство не должно иметь юридического права определять судьбу своего предприятия. Подобные случаи, которые, увы, нередки, мы рассматривать не будем.
Итак, предположим, что этот коэффициент соизмерения ?A введен. Тогда критерии Ф и ?A ?A имеют один порядок. Последнее означает, в частности, что мы можем, как это принято говорить в исследовании операций, сделать свертку обоих критериев, то есть заменить критерии Ф и ?A ?A одним. Провести свертку критериев можно бесчисленным множеством способов, каждый из которых является специальной гипотезой, о чем я буду говорить ниже. В данном случае удобно в качестве такого нового критерия ввести величину
WA = min(? ?A ?A)
Таким образом, значение нового критерия определяется наименьшим из чисел ?(YA) и ?A ?AYA.Напомним, что величину Y в мы считаем фиксированной.
Смысл введенного нового критерия можно пояснить с помощью рисунка (см. рис. 3). Величина ?A ?A(YA), очевидно, возрастает монотонно вместе с ростом капиталовложений в предприятие — YA Величина ? — степень очистки, наоборот, будет монотонно убывающей функцией Уд, поскольку чем больше денег будет израсходовано на реконструкцию предприятия, тем меньше у него останется денег на очистку воды. (Эти кривые изображены на прилагаемом рисунке.).
На этом же рисунке изображена пунктиром зависимость величины WA от YA если YA = 0, то есть все средства идут на очистку воды, то и дополнительная прибыль предприятия, полученная за счет его реконструкции, также равна нулю. Следовательно, и WA= 0. Точно так же и тогда, когда все деньги израсходованы на реконструкцию, качество воды будет самым плохим и W = 0. В этом случае прибыль будет высокой, но вода не будет очищаться совсем! Очевидно, что у величины W существует максимум. Мы обозначим его через YA.
Поскольку, как мы это предположили, субъект А сумел соизмерить ценность обоих критериев, то выбор величины YA, а следовательно, и затрат на очистку воды ХA = = QA — YA очевиден: субъекту А выгоднее всего выбрать величину YA равной ?A то есть равной тому значению, которое доставляет критерию WA максимальное значение.
Еще раз: когда деятельность человека оценивается не одним, а несколькими показателями, то для выбора своего способа действий он необходимо должен уметь соизмерить значения этих показателей при том или ином способе действий. Соотношение значений показателей определяет их объективное значение для данного субъекта, для его общественной стабильности, для его процветания в данных конкретных условиях.
Другое дело, что субъект может и не знать этого соизмерения: находится, например, в плену иллюзий или традиций и, наконец, просто совершать ошибки. Но существование величины ?A соизмеряющей показатели, — факт, объективно обусловленный внешними и внутренними условиями жизни того или иного социального организма, — это «внутренний компромисс» субъекта.
Итак, объективные цели субъекта А мы можем записать в следующем виде:
WA(YA, YB) ? max.
Это выражение означает, что субъект А стремится так выбрать соотношение средств, выделяемых им на развитие предприятия и очистку воды, чтобы доставить максимальное значение функционалу (показателю) WA. В таком виде могут быть записаны и цели субъекта В:
WB(YA, YB) ? max.
Я уже заметил, что свертка критериев — замена двух показателей одним — это тоже некоторая гипотеза, как и выбор коэффициента-соизмерителя А. Но природа этой гипотезы совершенно отлична от той, которая определяет выбор параметра А. В последнем случае этот «соизмеритель» объективно существует, но субъект его может не знать точно. Что же касается замены двух показателей одним, то это акт субъективный. Можно делать эту замену и по-другому. Однако предложенная свертка в данной ситуации естественна, она означает, что каждый из субъектов стремится в максимальной степени улучшить худший из показателей.
Эти правила выбора полностью решали бы проблему, если бы действия субъектов были бы независимы. Но величина показателя, оценка собственного положения партнером А, например, зависит от величины YB, которая находится в распоряжении другого субъекта. Точно так же и WB зависит не только от выбора субъекта В, но и от того, как распорядится своими ресурсами субъект А.
Значит, в этих условиях взаимозависимости субъектов А и В любое индивидуальное решение без учета действий другого субъекта будет не просто неоправданным или необоснованным. Оно может оказаться по-настоящему вредным или даже опасным для субъекта, принимающего решение. В этом случае нельзя обойтись без коллективного, согласованного решения или кооперативного решения, если использовать терминологию, принятую в теории конфликтов. Это кооперативное решение и процедуры его выработки мы и назвали «институтами согласия». Такие соглашения, как я уже об этом говорил, должны быть взаимовыгодными и эффективными.
Так вот, основным результатом, основной заслугой теории Гермейера — Вателя является доказательство существования в конфликтных ситуациях, подобных той, которую мы изучаем в этом параграфе (а она, по нашему определению, конфликтна, поскольку показатели WA и WB различны), взаимовыгодного и эффективного компромисса.
Другими словами, в данной ситуации институт согласия возможен, и процедуры выработки кооперативного соглашения, как мы увидим, достаточно просты.
Очень важно, что авторы дали четкие правила отыскания этого кооперативного решения. Это правило можно сформулировать в следующем виде: коллективным, то есть совместным, выбором величин YA и YB должны быть величины YA = YA* YB = YB*, удовлетворяющие следующим условиям:
WA(YA*,YB*) = max WA(YA*,YB*);
YA
WB(YA*,YB*) = max WB(YA*,YB*).
YB
Решение, которое формально определяется этими выражениями, носит в математике название ситуации равновесия. Значит, теория утверждает, что взаимовыгодным и эффективным, то есть неулучшаемым, коллективным соглашением в подобных конфликтах будет ситуация равновесия.
Но надо еще уметь найти это состояние равновесия. Оказалось, что и это сделать не очень сложно. В теории Гермейера — Вателя показано: для того чтобы величины YA* и YB* определяли ситуацию равновесия, необходимо и достаточно, чтобы они были решениями следующей системы уравнений:
?(QA — YA*; QB— YB*) = ?A?A(YA*);
?(QA — YA*; QB— YB*) = ?B?B(YB*);
Итак, оказывается, чтобы построить «институт согласия», то есть найти такие кооперативные соглашения, которые не только выгодны всем участникам, но и являются эффективными (неулучшаемыми одновременно для всех партнеров рассматриваемой конфликтной ситуации), достаточно решить относительно простую систему уравнений. Если, конечно, в распоряжении исследователей есть вся необходимая информация.
Здесь я рассказал о фрагментах теории конфликтов на примере ситуации, которая особенно проста. Но и в более сложных случаях задача отыскания взаимовыгодных компромиссов, когда степень достижения общей цели монотонно зависит от вкладываемого ресурса, достаточно проста с точки зрения математика.
Главная трудность в отыскании компромисса состоит не в математике и не в расчетах. При построении «институтов согласия», как это видно из рассмотренного примера, необходимо знать структуру «целевых функций» ? и ? — как зависит степень очистки воды от вложенных средств, как зависят дополнительные доходы предприятий, их конкурентоспособность от вкладываемых капиталов и, наконец, как соотносятся основные показатели, то есть каковы коэффициенты ?A и ?B.
Последнее, может быть, самое трудное, поскольку при соизмерении показателей весьма большую роль играет субъективный фактор. Но эти трудности компенсируются одной замечательной способностью кооперативных соглашений подобного рода: чем точнее каждый из субъектов представит исследователю, формирующему компромисс, свою информацию, тем выгоднее будет для него самого кооперативное соглашение. Возможные ошибки, а также и прямая ложь только снижают эффективность «институтов согласия». Поэтому, если соглашение заключается повторно, каждый из субъектов будет иметь возможность (и будет стремиться ее использовать) уточнить те данные, которые он предоставляет исследователю для выработки соглашения и которые раньше были ему плохо известны.
| <<< Назад Пример простейшего кооперативного соглашения |
Вперед >>> Некоторые комментарии |
- Еще раз о рациональной организации общества
- Коллективные решения и «институты согласия»
- Пример простейшего кооперативного соглашения
- Ситуация «путешественников в одной лодке»
- Некоторые комментарии
- «Институты согласия» в условиях экстремальных нагрузок на биосферу
- Подведем некоторые итоги
- Еще раз о проблемах коэволюции
- Ситуация «путешественников в одной лодке»
- Устойчивость к стрессорным ситуациям – это скорость угасания стрессорной реакции
- Ситуация в РФ (Восточной части Руси) и «Малой» Руси («Украине»)
- 100 великих русских путешественников
- Переправа электрических путешественников
- 11.1. Правовая ситуация и реализованные проекты
- 3.1. Ландшафтная структура, землепользование и экологическая ситуация
- Глава 8 Эколого-географическая ситуация в бассейнах трансграничных рек
- Проверено на себе (несколько слов об авторе)
