Книга: Энергия жизни. От искры до фотосинтеза
Глава 6. ДВИЖУЩИЕСЯ ЧАСТИЦЫ
| <<< Назад Глава 5. ТЕПЛОВЫЕ ПОТОКИ |
Вперед >>> Глава 7. ЧАСТИЦЫ, УДЕРЖИВАЕМЫЕ ВМЕСТЕ |
Глава 6.
ДВИЖУЩИЕСЯ ЧАСТИЦЫ
Еще со времен Джоуля, Кельвина, Майера, Гельмгольца и Клаузиуса, со времен открытия двух великих законов термодинамики, точного представления о том, что же такое тепло, не существовало. По крайней мере, такого, которое удовлетворило бы работающих с теплом ученых.
Это совершенно не означает, что законы термодинамики неполноценны, — они основаны на наблюдениях и не зависят от природы тепла. Однако с практической точки зрения этот факт осложнял применение законов термодинамики к каким-либо иным энергетическим устройствам, кроме тепловых машин, — к тем, где отсутствует тепловой поток.
Например, человеческий организм — главный предмет рассмотрения данной книги — определенно работает, и при этом температура его (37 °С) однородна и постоянна.
Разве это не является нарушением второго закона термодинамики? Мы уверены, что не является, но для того, чтобы четко понимать, почему именно не является, надо понять новую концепцию тепла как такового, выдвинутую впервые около 1800 года, а окончательно принятую научным сообществом только в 1860 году.
Начнем с того, что среди прочих над природой тепла размышляли и такие ученые, как Галилей и Ньютон. Они (и не только они) представляли себе тепло как движение мельчайших частиц материи. Для них это было вполне естественное предположение, поскольку эти великие ученые, исследуя в первую очередь законы движения и представляя тепло одной из форм движения, стремились вписать его в рамки своих грандиозных обобщений.
Однако в XVIII веке принято было представлять тепло как невесомый нематериальный ток. Такую точку зрения впервые выдвинул голландский физик Герман Бургаве примерно в 1700 году. В общем-то никаких объективных причин считать, что тепло представляет собой движение или вибрации, либо предполагать, что в горячих телах это движение или эти вибрации происходят быстрее, чем в холодных, не было. Разговоры о том, что, мол, существуют некие микрочастицы, слишком маленькие для того, чтобы их можно было увидеть, и вибрирующие слишком быстро и малоамплитудно для того, чтобы это можно было заметить, дети «эпохи рассудка» могли воспринимать только как заумную фантасмагорию.
Точнее говоря, в 1738 году профессор-математик из Санкт-Петербурга, столицы России, которого звали Даниил Бернулли, показал, что если представить газы состоящими из крошечных частиц, то из этого можно сделать вывод, что за давление газа отвечает движение этих частиц. Более того, предложенная им математическая модель, при которой скорость этих частиц возрастает по мере повышения температуры, в точности описывала реальные данные наблюдений. Однако его современники сочли эту теорию не более чем забавной спекуляцией. Большинство ученых предпочли принять на вооружение теорию теплорода — невесомого флюида, содержащегося в веществах, поскольку уже тогда было известно (по крайней мере, в представлении общественности) немало подобных флюидов в других областях: свет, электричество, магнетизм и т. п. Все были уверены в существовании такого явления, как «флогистон», — считалось, что его испускает в воздух любое вещество, сгорая или ржавея. Почему бы теплу не быть чем-то подобным? Так и сочли, и флюид тепла получил название «теплород».
Представление об одном из таких флюидов было торжественно похоронено в 1770-х годах, когда Лавуазье опроверг гипотезу о существовании флогистона, заменив ее тем представлением о природе горения и ржавления, которое мы разделяем и сейчас. Он показал, что при этих процессах не теряется или приобретается флогистон, а происходят химические реакции с содержащимся в воздухе кислородом. Однако существование теплорода тот же Лавуазье подтвердил, подкрепив эту теорию собственным авторитетом величайшего химика своего времени. Благодаря его заступничеству теория теплорода продержалась еще полвека, несмотря на лавинообразный рост фактов, свидетельствующих против нее.
Первые эксперименты, результаты которых однозначно указывали на ошибочность поддерживаемой Лавуазье теории теплорода, провел эмигрант из Америки Бенджамин Томпсон. Томпсон был тори и бежал из Америки во время Войны за независимость. Впоследствии, в 1791 году, курфюрст Баварский пожалует ему графский титул, и новоиспеченный граф вскоре женится, как ни забавно, на вдове самого Лавуазье. В историю он попал под именем графа Рамфорда.
В 1798 году граф Рамфорд наблюдал за высверливанием пушечного жерла в одной из оружейных мастерских курфюрста. В процессе погружения сверла в металлический цилиндр выделялось очень много тепла. Чтобы избежать перегрева, отверстие, в котором работало сверло, заливали водой и постоянно подливали ее по мере выкипания.
Сторонники теории теплорода не могли отрицать, что при такого рода трении вырабатывается тепло, и объясняли это так: металлический предмет всегда содержит тепло, а когда сверло вскрывает поверхность предмета, тепло выходит наружу. Рамфорд отметил в связи с этим два факта. Во-первых, количество содержащегося в металле тепла кажется бесконечным — сколько его ни сверли, тепло не перестает вырабатываться. А во-вторых, даже сточившееся сверло, уже практически не углубляющееся в металл, все равно производит не меньше тепла — а строго говоря, даже больше.
Рамфорду пришло в голову лишь одно вразумительное объяснение, почему при сверлении вырабатывается тепло — потому что в него переходит производимая работа. Рамфорд даже придумал единицу измерения механического эквивалента тепла на полвека раньше Джоуля, но выбранное им значение было слишком уж велико. Граф решил, что работа и тепло — тесно взаимосвязанные явления, и, поскольку работа, за которой он наблюдал, представляла собой механическое движение, Рамфорд заключил, что тепло тоже должно представлять собой одну из форм механического движения.
Через год, в 1799 году, близкий по сути эксперимент провел английский химик Гемфри Дэви. Он взял два куска льда и стал тереть их друг о друга с помощью механического устройства при температуре чуть ниже точки замерзания воды. Согласно господствовавшей на тот момент теории теплорода, при такой температуре лед просто не мог содержать в себе достаточно теплорода, чтобы растаять. Однако в процессе трения лед все же начинал таять. Дэви, как и граф Рамфорд, сделал вывод, что энергия движения переводится в тепло, а значит, тепло — это одна из форм движения.
Несмотря на это, теория теплорода господствовала в умах еще несколько десятков лет.
Поколебать ее господство удалось не путем изучения тепла как такового, а путем изучения материи. XVII и XVIII века стали периодом постепенного накопления знаний о свойствах газов. В четвертой главе уже упоминалось о законах Бойля и Шарля. Все эти знания просто взывали к тому, чтобы свести их в единую теорию вроде той, которую безуспешно пытался продвинуть Бернулли.
И вот в 1803 году английский химик Джон Дальтон продвинулся еще дальше. Он предположил, что не только газы, но и вообще любое вещество состоит из крошечных частиц, слишком маленьких, чтобы их можно было увидеть, неделимых и неразрушимых. Он назвал такие частицы «атомами». Этот термин происходит из древнегреческой философии, поскольку еще среди древних греков были философы, которые придерживались сходных взглядов. Однако греки в свое время не увидели в этих теориях ничего, кроме пустых рассуждений, и отвергли их. А Джон Дальтон — и это принципиальная разница! — положил в основу своих выводов строгие экспериментальные данные.
Несмотря на это, теория Дальтона не сразу овладела умами химиков — скорее всего, из-за того, что уложить в голове представление о существовании каких-то частиц, слишком малых для того, чтобы быть заметными в принципе, очень сложно. Но мало-помалу стало выясняться, что эта теория в силах дать ответ на многие вопросы. В ее рамках описывались не только свойства газов (как в теории Бернулли), но и многие свойства химических реакций твердых и жидких веществ. Все реакции обретали единую логику, если рассматривать их как взаимодействие различного рода атомов, связанных в определенные группы (позже их назовут «молекулами»), которые распадаются, чтобы дать возможность образовавшим их атомам связаться уже по-другому. Сами по себе атомы так и продолжали оставаться невидимыми, но преимущества, которые несла с собой теория атомов в отношении понимания свойств вещества, понемногу заставляли ученых ее принять.
Датировать завершение этого процесса можно 1858 годом, когда итальянский химик Станислао Канниццаро опубликовал трактат, где химические явления объяснялись через теорию атомов. Приводимые им объяснения были столь четкими и ясными, что непонимания не осталось уже ни у кого. Два года спустя на конференции химиков в Карлсруэ (Германия) Канниццаро активно отстоял эту теорию, убедив присутствующих как фактическими свидетельствами, так и силой собственного авторитета. С этого момента теория атомов стала единственной господствующей и продолжает оставаться таковой по сей день, хотя на сегодня об атомах известно уже, что они сами по себе гораздо сложнее тех неделимых маленьких шаров, лишенных собственных свойств, какими описывали их Дальтон и Канниццаро.
Взирая на материю, и в первую очередь на газы, как на совокупность одиночных атомов или, чаще, групп атомов, именуемых молекулами, логично было вернуться к давнишним рассуждениям Бернулли о том, как свойства газов можно объяснить через движение составляющих их частиц. Были проведены дополнительные эксперименты, результаты которых интерпретировались уже в свете теории атомов.
К примеру, Джоуль, проводя в 1840-х годах свои эксперименты по превращению всеми возможными способами работы в тепло, исследовал расширение газов такими способами, при которых работа не была задействована. Расширяясь, газы не толкали никаких поршней и не приводили в движение никаких предметов. Они просто расширялись в пустоту. Когда это происходило, Джоуль замерял температуру газов и сперва не обнаруживал ни ее повышения, ни понижения, как и ожидалось от процесса, в котором не задействована работа.
Однако в 1852 году, работая вместе с Томсоном (который позже станет лордом Кельвином), он установил, что на самом деле в таких случаях все же происходит небольшое понижение температуры. Это явление до сих пор называют «эффектом Джоуля—Томсона». Понижение температуры свидетельствует о том, что расширение газа на самом деле не является процессом, где не задействовано никакой работы. Молекулы газа испытывают друг к другу слабое притяжение, и движение против силы этого притяжения и есть тот момент, где совершается работа. Энергия, необходимая для совершения этой работы, берется из теплового содержания газа, так что в результате температура несколько падает.
Наличие этой силы межмолекулярного притяжения несколько усложняет расчеты, которыми должны описываться свойства газа, но химики-теоретики упростили себе жизнь, взяв за материал для своих формул некий воображаемый «идеальный газ», в котором сила притяжения между молекулами равна нулю, как и суммарный объем самих молекул.
Строго говоря, описываемая таким образом ситуация невозможна, но ее изобретение настолько упрощает расчеты, что позволяет теоретикам выводить из них простые законы. Эти законы приблизительно справедливы для реальных ситуаций и, будучи однажды сформулированными, в дальнейшем могут подвергаться всевозможным уточнениям для каждого конкретного случая. Это явно более благодарный подход, чем пытаться с самого начала математически просчитывать все детали реальных ситуаций.
И закон Бойля, и закон Шарля в точности применимы только к идеальному газу, и если свести их воедино, то мы получим простое «уравнение состояния газов», которое описывает состояние таких параметров газа, как температура, давление и объем. Зная любые два из этих параметров, можно сразу же высчитать третий. В отношении реальных газов результат таких расчетов будет соответствовать действительности лишь приблизительно (хотя порой очень близко к точному). Однако уравнение состояния газов вполне можно модифицировать таким образом, чтобы в нем учитывались и сила межмолекулярного притяжения, и объем молекул. Голландский физик Йоханнес Дидерик ван-дер-Ваальс с большим успехом привел одну из таких модификаций в 1873 году.
Я надеюсь, что это объяснит тот факт, что в течение 1850-х годов множество исследователей (в том числе и Клаузиус), прекрасно зная, что на самом деле это не так, продолжали дорабатывать работу Бернулли исключительно для газов с нулевым объемом частиц, не оказывающих друг на друга никакого воздействия. В результате родилась кинетическая теория газов, то есть теория, рассматривающая частицы в движении.
До совершенства эту теорию довели шотландский математик Джеймс Кларк Максвелл и австрийский физик Людвиг Больцман в 1859 году и за несколько последующих лет. Итогом их математического подхода (в условия которого входило, что молекулы газа движутся по прямой в случайно выбранных направлениях и сталкиваются друг с другом и со стенками камеры с абсолютной упругостью, не теряя при столкновении энергии) стало установление связи скорости движения молекул с температурой газа.
Представьте себе, что две молекулы газа столкнулись. Они отскакивают в разные стороны, изменив после столкновения направление движения и, вероятнее всего, скорость. Однако суммарный импульс системы остается при этом постоянным (см. главу 3), так что скорости, которые обе частицы могут иметь после столкновения, далеко не произвольны.
Но даже в этом случае распределение скоростей частиц после столкновения может быть различным. Если, к примеру, быстро движущаяся молекула сталкивается с медленно движущейся, то может получиться так, что медленная остановится, а быстрая отлетит в сторону еще быстрее, чем раньше, обладая всем суммарным импульсом обеих молекул до столкновения. Возможно также (причем куда более вероятно), что в результате скорости обеих молекул изменятся в сторону усреднения — быстро движущаяся молекула станет двигаться медленнее, а медленно движущаяся — быстрее.
Это можно наблюдать на примере бильярдных шаров. Во времена Максвелла атомы и молекулы так и представляли в виде сверхмалых бильярдных шаров. Сейчас их представляют уже не так; на самом деле сейчас уже известно, что строение их настолько сложно, что их невозможно представить в виде чего бы то ни было нам знакомого, не покривив при этом душой. Однако для описаний в рамках кинетической теории газов аналогии с бильярдными шарами вполне достаточно.
Предсказать, как именно перераспределятся скорости двух конкретных молекул после их столкновения, невозможно. Однако в отношении бессчетного множества квинтиллионов столкновений (а именно столько их и происходит каждую секунду в любом объеме газа, достаточно большом, чтобы его можно было увидеть) вполне допустимо использовать статистические методы для установления среднестатистического распределения скоростей. С их помощью можно показать, что молекулы любого заданного объема газа имеют некую «наиболее вероятную» скорость, к которой в той или иной степени тяготеют все молекулы этого объема. В любой отдельно взятый момент времени одни молекулы будут двигаться чуть (или значительно) быстрее этой «наиболее вероятной» скорости, другие — чуть (или значительно) медленнее.
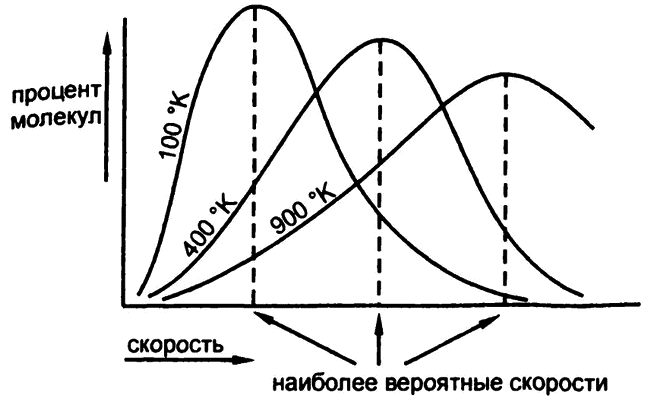
Рис. 5. Скорость молекул и температура
Довольно сложное математическое выражение, получившее название «статистический закон распределения Максвелла—Больцмана» (рис. 5) в честь разработавших его ученых, позволило подсчитать процентное соотношение молекул любого заданного объема газа, относящихся к группам с различным значением скорости (при условии, что известны температура газа и масса составляющих его молекул). Если изобразить эту формулу в виде графика отношения скорости к процентному соотношению обладающих данной скоростью молекул, то получим плавную кривую, достигающую пика на значении равном «наиболее вероятной» скорости, а затем — так же плавно снижающуюся.
Теперь можно провести прямую связь между температурой и движением молекул газа. В любом газе, при любой температуре скорость отдельных молекул может принимать значения от нуля до крайне высокой. Однако наиболее вероятная скорость оказалась находящейся в прямой пропорции к квадратному корню от абсолютного значения температуры. По мере повышения температуры наиболее вероятная скорость молекул газа увеличивается. Если абсолютная температура возрастает в четыре раза, то наиболее вероятная скорость молекул — в два.
Так что для любого отдельного газа температура является величиной, тесно привязанной к наиболее вероятной скорости молекул. Однако для того, чтобы корректно обобщить это правило для любых газов, надо принять в расчет массу молекул этого газа. При любой заданной температуре, согласно формуле Максвелла—Больцмана, наиболее вероятная скорость обратно пропорциональна квадратному корню этой массы. Чем массивнее молекулы, тем медленнее они движутся. Молекула кислорода в шестнадцать раз массивнее молекулы водорода, поэтому молекула водорода движется в четыре раза (четыре — квадратный корень из шестнадцати) быстрее, чем молекула кислорода при любой заданной температуре.
Но кинетическая энергия, как уже объяснялось в главе 3, равняется произведению половины массы на квадрат скорости, и вкупе со всеми только что приведенными данными мы получаем, что при любой заданной температуре средняя кинетическая энергия молекул всех газов одинакова. Молекулы одного газа могут быть массивнее молекул другого, но тогда они обладают меньшей скоростью; если же их масса меньше, то и скорость их соответственно выше. Так или иначе, произведение массы на квадрат скорости будет во всех случаях одинаково. А поскольку скорость увеличивается пропорционально квадратному корню температуры, то и кинетическая энергия, пропорциональная квадрату скорости, является прямо пропорциональной температуре (см. рис. 5).
То есть можно сказать, что словом «температура» мы называем среднюю кинетическую энергию молекул, из которых состоит газ.
Оказалось, что это отношение справедливо для всех веществ, не только для газов. Точнее, для жидкостей и твердых тел сильно отличаются только условия. Молекулы, составляющие газ, находятся далеко друг от друга и движутся независимо. В жидкостях молекулы находятся в постоянном контакте и могут лишь скользить друг по другу, а в твердых телах — вообще жестко закреплены в общей структуре и даже скользить не могут. Тем не менее молекулы жидкостей начинают скользить друг по другу, а молекулы твердых тел — вибрировать на своих жестко установленных местах с большей энергией по мере возрастания температуры.
Аналогичным образом по мере понижения температуры все вещества теряют энергию, и при абсолютном нуле энергетическое содержание всех веществ сводится к минимуму. Собственно, до последнего времени принято было считать, что этот минимум равен нулю, но современная теория говорит о том, что даже при абсолютном нуле в веществе остается некий неизвлекаемый минимум энергии. Это объясняет, в частности, странные свойства гелия при температурах близких к абсолютному нулю.
Теперь давайте представим, что некий объем горячего газа вошел в соприкосновение с другим объемом холодного газа. Кинетическая энергия молекул горячего газа в среднем выше, чем молекул холодного газа. При столкновении двух молекул из разных объемов, скорее всего, кинетическая энергия «горячей» молекулы будет больше, чем «холодной», несмотря на то что вполне возможны и противоположные сочетания. Если вас смущает последняя оговорка, представьте себе такую аналогию: уровень жизни в США выше, чем уровень жизни, скажем, в Египте, так что наугад выбранный американец с преобладающей вероятностью окажется богаче наугад выбранного египтянина, хотя, конечно, в Египте можно найти людей, которые будут богаче многих американцев.
Точно таким же образом, не исключено, что в результате столкновения «горячая» молекула получит еще больше энергии за счет «холодной» молекулы и станет еще «горячее». (Понятно, почему я взял слова «холодная» и «горячая» в кавычки, — потому что отдельная молекула в принципе не может быть ни холодной, ни горячей, эти понятия применимы только в целом к системам, состоящим из огромного числа молекул.) Однако с большей вероятностью «горячая» молекула энергию потеряет, а «холодная» — получит, и обе останутся с неким усредненным количеством энергии, а значит — и температуры.
При большом количестве столкновений лишь единицы приведут к увеличению разности энергий участвовавших в них молекул, а подавляющее большинство — к уменьшению этой разности. Вероятность того, что при единичном столкновении «горячая» молекула приобретет энергию, а «холодная» — потеряет, мала, но вероятность того, что такая случайность повторится многократно, еще меньше.
Следовательно, в ходе множества случайных столкновений средняя кинетическая энергия молекул, а значит и температура, горячего газа (как и любого другого горячего предмета) уменьшится при контакте с холодным газом (или любым другим холодным предметом), а температура холодного, — наоборот, увеличится. Тепло будет перетекать от горячего предмета к холодному, пока средняя кинетическая энергия всех молекул обоих предметов не приобретет некое общее усредненное значение.
В чем отличия такого представления от старой теории тепла, как нематериального тока? Согласно старой теории, тепло перетекало от объектов с высокой температурой к объектам с низкой, повинуясь второму закону термодинамики, не подразумевающему ни исключений, ни модификаций. Согласно же кинетической теории, поток тепла есть среднестатистический результат случайных столкновений, который теоретически может оказаться и иным, так что второй закон термодинамики больше не может считаться абсолютно неизбежным. В принципе не исключено такое стечение обстоятельств, что множество «горячих» молекул наберут энергию из «холодных» и тепло перетечет, таким образом, из холодного предмета к горячему. То есть кинетическая теория не считает невероятным, что вода в чайнике, поставленном на огонь, не закипит, а замерзнет и огонь станет еще жарче.
Вероятность такого события (просчитанная на основе уравнений Максвелла) настолько ничтожно мала, что даже если бы вся Вселенная состояла только из стоящих на огне чайников, то шансов дождаться, чтобы хоть один из них замерз за все время существования Вселенной, у нас все равно не было бы практически никаких.
Разница между неизменным потоком тепла и потоком, испытывающим постоянные колебания, с философской точки зрения, конечно, огромна, но с практической настолько незначительна, что Максвеллу пришлось специально изобретать способ ее хоть как-то подчеркнуть. Поэтому он придумал крошечное существо, которое с заслонкой сидит на трубе, соединяющей две камеры с газом, температура в которых сначала одинакова. Существо, выдуманное Максвеллом, занималось следующим: когда к трубе подлетала из правой камеры быстро движущаяся молекула, оно пропускало ее через трубу, а медленные — не пропускала. Из левой же камеры оно, наоборот, пропускало все медленные молекулы, а быстрые — нет. Таким образом, в левой камере собирались быстро движущиеся молекулы, и сама камера нагревалась, а в правой — медленно движущиеся, и камера остывала. Таким образом, тепло перетекало бы из холодной камеры в горячую, что для старой теории тепла было неприемлемо, а для кинетической — вполне допустимо. Это воображаемое существо было названо «демоном Максвелла», и с тех пор этот «демон» известен как идеальный борец с энтропией.
Впрочем, подобные демоны водятся не только в наших фантазиях. В реальной жизни тоже существует некий аналог «демона Максвелла». Среднестатистические свойства молекул столь близки к неизменным только потому, что при обычных обстоятельствах мы имеем дело с телами, состоящими из огромного количества молекул. По мере уменьшения количества молекул в системе шансы наткнуться на заметное отклонение от среднестатистической вероятности возрастают. Когда речь идет о действительно малых количествах, ровное единообразие полностью пропадает.
В качестве такого примера можно назвать наблюдение, которое произвел в 1827 году шотландский ботаник Роберт Броун, отметивший, что цветочная пыльца, будучи распыленной в воде, как-то странно шевелится то в одном, то в другом направлении, очевидно, случайным образом. Сначала он решил, что пыльца движется сама, поскольку в ней скрыта живая сила, но вскоре обнаружилось, что подобным образом шевелятся и любые другие маленькие предметы (например, распыленные красители). В честь первооткрывателя это явление было названо «броуновским движением».
Примерно в 1890 году Больцман продемонстрировал, что броуновское движение можно объяснить с помощью кинетической теории. Он отметил, что любой находящийся в воде предмет со всех сторон подвергается бомбардировке молекулами окружающей его воды. Статистически количество ударов, получаемых им с одной стороны, будет уравновешиваться количеством ударов, получаемых с другой, и в итоге предмет будет оставаться неподвижным.
Понятно, что точно равным количество ударов с обеих сторон не будет, но при обычных обстоятельствах это не важно, разница будет незначительна. Если с одной стороны предмет получил квинтиллион ударов, а с другой в этот же момент — квинтиллион и двенадцать, то такое неравенство останется незамеченным. Однако при уменьшении размеров находящегося в воде тела общее число ударяющих по его площади одновременно молекул тоже уменьшится, и то же самое небольшое неравенство станет ощутимее. Если взять настолько маленькое тело, что одновременно в него будут ударять лишь сто молекул с одной стороны и сто двенадцать — с другой, эти двенадцать ударов разницы, незаметные в первом случае, теперь могут оказать вполне реальное воздействие. Больцман продемонстрировал, что применительно к очень малым телам случайное движение молекул, при котором возникает перевес ударного воздействия то в одну, то в другую сторону, вполне может привести к поведению характеризуемому броуновским движением.
Таким образом, мы имеем дело со своего рода демоном Максвелла, шевелящим тела, которым по прежней теории предназначено было пребывать в неподвижном состоянии. Поскольку движения частиц строго хаотичны, то никакой направленности в долгосрочной перспективе в отношении крупных тел в них просматриваться не может.
В 1905 году Альберт Эйнштейн разработал точную математическую модель броуновского движения, а в ходе точных экспериментов 20-х и 30-х годов XX века были измерены даже скорости движения молекул в газах, и оказалось, что их распределение в точности соответствует расчетам кинетической теории.
Энтропию тоже можно рассматривать в свете кинетической теории. Однако сначала разберемся в значениях слов «порядок» и «хаос».
Интуитивно мы называем «порядком» любое положение вещей, в котором присутствует некая математическая или логическая закономерность. Если же никакой системы в положении вещей вычленить невозможно, мы называем это хаосом.
Можно сказать так: порядок — это когда одну часть системы можно отличить от другой, а хаос — когда четкой границы нельзя провести нигде. Чем более четки различия между частями системы, тем более она упорядоченна.
Часто используемым примером упорядоченной системы является колода карт, где все карты сгруппированы по мастям и карты каждой масти расположены по старшинству. Заранее известно, что первая карта — пиковый туз, вторая — пиковый король и так далее по всем остальным мастям. Можно точно определить порядковый номер любой карты в колоде.
Если же разбивка колоды по мастям сохраняется, но в пределах каждой масти карты не расположены по старшинству, такая система уже менее упорядоченна. В отношении любой пиковой карты можно сказать только то, что она находится «где-то в первой четверти колоды», но точнее определить ее местонахождение уже невозможно.
Если же колода хорошо перетасована, то вообще ничего невозможно сказать ни об одной из карт. В этом случае мы имеем дело со «случайным распределением», то есть с хаосом.
Теперь давайте представим себе ситуацию возрастающей энтропии, например перехода тепла от горячего тела к холодному (это классический пример увеличения энтропии). По мере перетекания тепла горячее тело охлаждается, а холодное — нагревается, пока оба они не будут иметь некую среднюю температуру.
Во время этого процесса увеличивается не только энтропия, но и хаос. В частности, до начала теплопередачи оба тела (горячее и холодное) легко отличить друг от друга хотя бы по их температуре, если даже они и являются совершенно одинаковыми во всех остальных отношениях. По мере перетекания тепла от одного к другому разница между ними становится все меньше и в конце концов исчезает полностью.
Опять же, если свести вместе объем кислорода и объем водорода, температура и давление в которых равны, то они перемешаются, пока общий объем не будет содержать равномерную смесь обоих газов. Поскольку это спонтанный процесс, значит, при нем происходит возрастание энтропии. И поскольку в результате два легко различимых объекта становятся неразличимы, то, значит, хаос при этом тоже возрастает.
На самом деле в каждом конкретном случае можно провести параллели между возрастанием энтропии и возрастанием хаоса. Энтропия и хаос — это аналогичные явления.
Поскольку все спонтанные процессы подразумевают увеличение энтропии, то, значит, они подразумевают и увеличение хаоса. Странно было бы ждать, что тепло будет само по себе переходить от холодного тела к горячему, а смесь газов — сама по себе рассортировываться на составляющие.
Это утверждение справедливо и в отношении самого первого из наших примеров — колоды карт. Сложенная упорядоченным образом колода сама по себе, конечно, не перетасуется, но это лишь потому, что она вообще не будет подвергаться никаким изменениям. Но предположим, что мы создадим некие условия, при которых колода будет подвергаться неким изменениям, причем таким, которые будут определяться исключительно случайным образом. Например, если мы сбросим карты с крыши дома на мостовую. Тогда колода разлетится на отдельные карты. Если теперь эти карты собрать, не глядя на их достоинство, то в результате мы получим совершенно случайную последовательность, несмотря на то что начинали они свой полет в строгом порядке. Таким образом, мы имеем очередной спонтанный процесс, в котором возрастают и энтропия, и хаос.
Перетасовывание карт — тоже пример спонтанного процесса (в том смысле, что карты при нем распределяются случайным образом), при котором возрастают как энтропия, так и хаос. На самом деле честное перетасовывание карт случайным образом — обязательное условие для честной игры в карты.
Для того чтобы перевести колоду карт обратно из хаотичного в упорядоченное состояние, необходимо сесть и разложить ее, уделяя внимание каждой карте (то есть, в терминологии нашей первой главы, необходимо «совершить усилие», уменьшая энтропию). Глупо было бы ждать, что колода вдруг придет в упорядоченное состояние сама собой, если ее долго перетасовывать или подбрасывать в воздух.
Точнее, существует ненулевая вероятность, что перетасовывание колоды может привести к образованию где-то в ней коротенькой упорядоченной последовательности или даже длинной — ведь бывает же, что при сдаче на руках у одного играющего оказывается тринадцать пик. Это явление того же порядка, что и замерзание воды в поставленном на огонь котелке. Разница лишь в масштабах вероятности — увидеть на руках тринадцать пиковых карт вполне возможно лишь потому, что их в колоде всего пятьдесят две. Если бы карт в колоде было столько же, сколько молекул в котелке с водой, то и шансы вытащить случайным образом четверть из них так, чтобы все вытянутые карты оказались одной масти, были бы такими же ничтожными, как и увидеть замерзающую воду в котелке.
Из всех форм энергии тепло больше всех тяготеет к хаосу. То есть вещества, отличающиеся друг от друга только тепловым содержанием, труднее различить, чем вещества, отличающиеся количеством излучаемого света или положением в гравитационном или электромагнитном поле. Следовательно, во всех спонтанных процессах, где используется нетепловая энергия, часть энергии всегда переходит в тепло, что само по себе является примером возрастания энтропии.
По той же логике, все содержащееся в системе тепло никогда не может быть полностью переведено в нетепловую энергию, поскольку такой процесс подразумевал бы уменьшение энтропии. В действительности же если часть тепла переводится в другую форму энергии, то энтропия в оставшейся части возрастает настолько, что более чем компенсирует свое снижение, получившееся в процессе перехода тепловой энергии в нетепловую.
Таким образом, очевидно, что кинетическая теория газов, разработанная во второй половине XIX века, удовлетворительным образом объясняет термодинамические явления, зафиксированные в наблюдениях первой половины столетия под влиянием теории теплорода.
Однако, как уже упоминалось в начале главы, в рамках этой новой теории объясняется и то, как человеческий организм может производить работу, сохраняя при этом свою температуру неизменной, чего прежняя теория объяснить не могла. Я этого не забыл, и мы методично движемся к выполнению обещанного. Важнейшими понятиями теперь для нас станут «атом» и «молекула» — понятия, которых в прежней теории не было, но в новой являющиеся краеугольными.
| <<< Назад Глава 5. ТЕПЛОВЫЕ ПОТОКИ |
Вперед >>> Глава 7. ЧАСТИЦЫ, УДЕРЖИВАЕМЫЕ ВМЕСТЕ |
- Глава 1. УСИЛИЯ, КОТОРЫЕ МЫ СОВЕРШАЕМ
- Глава 2. ПЛОДЫ ОГНЯ
- Глава 3. ИЗМЕРЯЕМОЕ ДВИЖЕНИЕ
- Глава 4. ИЗМЕРЯЕМОЕ ТЕПЛО
- Глава 5. ТЕПЛОВЫЕ ПОТОКИ
- Глава 6. ДВИЖУЩИЕСЯ ЧАСТИЦЫ
- Глава 7. ЧАСТИЦЫ, УДЕРЖИВАЕМЫЕ ВМЕСТЕ
- Глава 8. ТЕПЛО И ХИМИЧЕСКИЕ РЕАКЦИИ
- Глава 9. НАПРАВЛЕНИЕ РЕАКЦИИ
- Глава 10. ЭЛЕКТРИЧЕСКИЙ ПУТЬ
- Глава 11. КАК ПОДТОЛКНУТЬ РЕАКЦИЮ
- Глава 12. СТИМУЛЯЦИЯ БЕЗ ПРИЛОЖЕНИЯ ЭНЕРГИИ
- Глава 6. ДВИЖУЩИЕСЯ ЧАСТИЦЫ
- § 46 Ядерный распад и элементарные частицы
- Античастицы и антивещество.
- 248. Перемещаются ли вместе с волнами частицы воды?
- II. Как открывают субатомные частицы?
- IV. Каким образом частицы набирают весь свой вес? Золотой век кварков
- Глава пятая Элементарные частицы и силы в природе
- ГЛАВА 14. КАК РАСПОЗНАТЬ ЧАСТИЦЫ
- Бета-частицы оказались электронами
- Луна и элементарные частицы
- § 75 Наночастицы и перспективы нанотехнологий
