Книга: Сейчас. Физика времени

Скорости объектов и скорость света

Скорости объектов и скорость света

Здесь я покажу, почему скорость света одинакова во всех системах отсчета.

Если некоторый объект движется, мы можем обозначить как x₁ его координату в момент времени t₁ и как x₂ – его координату в момент t₂. Представьте, что на самом деле это два события. Скорость нашего объекта такова: v = (x₂ ? x₁)/(t₂ ? t₁) = ?x/?t. В другой системе отсчета: V = (X₂ ? X₁)/(T₂ ? T₁) = ?X/?T. Мы можем воспользоваться преобразованием Лоренца, чтобы сравнить эти две величины. Обозначим буквой u относительную скорость двух СО, чтобы можно было использовать v и V для обозначения скорости объекта в каждой из двух систем. Запишем преобразование для двух событий и вычтем одно из другого:

А теперь разделим одно уравнение на другое, чтобы исключить ?:

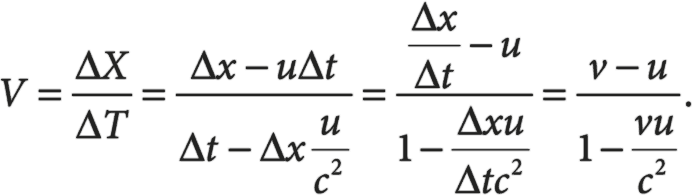
Это уравнение для преобразования скорости, позволяющее выразить скорость V во второй системе отсчета через v – скорость в первой системе отсчета.

Пусть v = c, то есть объект (к примеру, фотон) движется со скоростью света в первой СО. Во второй системе отсчета его скорость равна:

вне зависимости от u, относительной взаимной скорости двух систем отсчета. Если v = c, то V = c. Объекты, движущиеся со скоростью света в какой-то одной системе отсчета, движутся с той же скоростью и во всех остальных системах. Попробуйте подставить в уравнение v = ?c и посмотрите, что получится. Удивлены?

Аналогичный вывод показывает, что c не меняется даже при произвольном направлении света[277].

Этот результат объясняет неудачу опыта Майкельсона?Морли в 1887 году, когда исследователи хотели обнаружить разницу скорости света в двух направлениях, первое из которых параллельно движению Земли, а второе – перпендикулярно этому движению.