Книга: Наша математическая вселенная

Математика, везде математика

Математика, везде математика

Каков же ответ на главный вопрос жизни, Вселенной и всего такого? В книге «Автостопом по Галактике» Дугласа Адамса выясняется, что ответ на этот вопрос — 42, однако самой сложной частью задачи оказалось отыскание самого вопроса. В действительности, хотя наши любознательные предки задавались глобальными вопросами, их поиски «теории всего» менялись вместе с ростом знаний. По мере того как древние греки заменяли мифологические объяснения механическими моделями Солнечной системы, их акценты в этих вопросах смещались с почему на как.

С тех пор сфера наших вопросов сократилась в одних областях и разрослась в других (рис. 10.1). Некоторые вопросы отброшены как наивные или ошибочные, вроде объяснения размеров планетных орбит исходя из первичных принципов (это было популярно в эпоху Возрождения). То же самое может случиться с модными нынче попытками предсказания количества тёмной энергии в космосе, если окажется, что её плотность в наших окрестностях является исторической случайностью (гл. 6). Тем не менее наша способность отвечать на другие вопросы превзошла самые смелые ожидания прежних поколений. Ньютон был бы поражён, узнав, что мы сумели определить возраст Вселенной с точностью до 1 % и узнали устройство микромира в достаточной мере, чтобы сконструировать «Айфон».

Я считаю шутку Дугласа Адамса про 42 очень удачной, поскольку математика играет исключительную роль во всех этих успехах.[63] Та идея, что Вселенная в некотором смысле является математической, восходит по меньшей мере к пифагорейцам и породила многовековую дискуссию физиков и философов. Галилей утверждал, что Вселенная — это «величественная книга», написанная на языке математики. Лауреат Нобелевской премии по физике Юджин Вигнер в 60-х годах XX века настаивал, что «невероятная эффективность математики в естественных науках» нуждается в объяснении.

Фигуры, паттерны и уравнения

Мы переходим к рассмотрению по-настоящему радикального объяснения. Однако прежде необходимо уточнить, что именно мы пытаемся объяснить. Пожалуйста, оторвитесь на несколько секунд от чтения и оглядитесь. Где вся эта математика, которой мы собираемся заниматься? Разве математика — это не наука о числах? Вероятно, вам на глаза попадётся несколько чисел, например пагинация в этой книге, но это лишь символы, изобретённые и изображённые людьми, так что вряд ли они отражают математическую сущность Вселенной в каком-либо глубоком смысле.

Из-за нашей системы образования многие приравнивают математику к арифметике. Но математика, как и физика, пришла к постановке более глубоких вопросов. Например, в приведённой выше цитате Галилей говорит о геометрических фигурах вроде окружностей и треугольников как о математических. Видите ли вы вокруг себя геометрические узоры или фигуры? (Дизайн вроде прямоугольной формы книги не в счёт.) Но попробуйте бросить камешек и посмотрите, какую красивую форму придаёт природа его траектории! Галилей сделал замечательное открытие (рис. 10.2): траектория любых предметов имеет одинаковую форму, называемую перевёрнутой параболой. Более того, форму этой параболы можно описать простым уравнением: x = y², где x — горизонтальное положение, y — вертикальное положение (высота). В зависимости от начальной скорости и направления эта форма может растягиваться и по вертикали, и по горизонтали, однако она всегда остаётся параболой.

Когда мы наблюдаем, как объекты движутся по орбитам в космосе, мы открываем другую повторяющуюся форму, показанную на рис. 10.3 — эллипс. Уравнение x² + y² = 1 описывает точки, лежащие на окружности, а эллипс — это просто растянутая окружность. В зависимости от начальной скорости, направления движущегося по орбите объекта и массы, вокруг которой он движется, форма этой орбиты может оказываться растянутой или наклонённой, однако всегда остаётся эллипсом. Более того, оконечность сильно вытянутого эллипса почти точно совпадает с параболой, так что все эти траектории — просто части эллипсов.[64]

Рис. 10.2. Когда вы что-нибудь подбрасываете, траектория полёта предмета всегда имеет форму перевёрнутой параболы, если только он с чем-нибудь не столкнётся в полёте и если можно пренебречь сопротивлением воздуха.

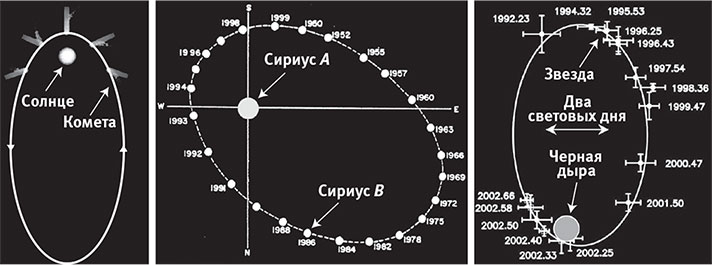
Рис. 10.3. Когда один объект обращается по орбите вокруг другого под действием гравитации, его орбита всегда имеет одну форму, эллипс, который представляет собой просто окружность, растянутую в одном направлении (так будет, если нет источников трения и если мы игнорируем эйнштейновские поправки к ньютоновской теории гравитации, которые обычно ничтожны, если мы не рядом с чёрной дырой). Орбита остаётся эллипсом для самых разных объектов: и для кометы, обращающейся вокруг Солнца (слева), и для белого карлика — мёртвой звезды, обращающейся вокруг Сириуса A, ярчайшей звезды нашего неба, и для звезды, обращающийся вокруг гигантской чёрной дыры в центре Галактики (справа), которая в миллион раз массивнее Солнца. (Рисунок справа воспроизводится с разрешения Рейнхарда Гензеля и Райнера Шедела.)

Рис. 10.4. Подобно тому, как изобразительное искусство и поэзия могут выразить многое с помощью немногих символов, так и физика способна сделать это с помощью уравнений. Слева направо и сверху вниз на этих шедеврах описаны: электромагнетизм, околосветовое движение, гравитация, квантовая механика и расширение Вселенной. Мы ещё не нашли уравнений единой «теории всего».

Постепенно люди открыли в природе множество других повторяющихся форм и паттернов, охватывающих не только движение и гравитацию, но и такие разные области, как электричество, магнетизм, свет, теплота, химия, радиоактивность и субатомные частицы. Эти паттерны складываются в законы физики. Как и форму эллипса, эти законы можно описать, применяя математические уравнения (рис. 10.4). Почему?

Числа

Уравнения — не единственный скрытый в природе намёк на математику: есть также числа. Я говорю не о творениях рук человеческих, вроде пагинации в этой книге, а о числах, которые выражают фундаментальные свойства нашей физической реальности. Сколько карандашей вы сможете расположить так, чтобы все они были перпендикулярны (под углом 90°) друг другу? Три: их можно разместить, например, вдоль трёх стыков стен и пола в углу вашей комнаты. Откуда взялось число 3? Мы называем его размерностью пространства, но почему существует именно 3 измерения, а не 2, 4 или 42? Почему в нашей Вселенной существует (насколько мы можем судить) ровно шесть типов кварков? Есть много других «встроенных» в природу целых чисел (гл. 7), которые описывают, какого типа элементарные частицы существуют.

И, вдобавок к математическим гостинцам, существуют закодированные в природе величины, которые не являются целыми числами и требуют для записи дробных значений. Согласно моим подсчётам, природа закодировала 32 таких фундаментальных числа. Относится ли к ним число, которое появляется на индикаторе весов, когда вы встаёте на них после ванны? Нет, оно не в счёт, поскольку является мерой чего-либо (вашей массы), что день ото дня изменяется, а значит, не является фундаментальным свойством нашей Вселенной. Что можно сказать о массе протона (1,672 622 ? 10^–27 кг) или о массе электрона (9,109 382 ? 10^–31 кг), которые кажутся неизменными во времени? Они также не в счёт, поскольку измеряются в килограммах, а это произвольная единица массы, придуманная людьми. Но если вы разделите одно из этих двух чисел на другое, получится нечто поистине фундаментальное: протон примерно в 1836,15 267 раз массивнее электрона.[65] Значение 1836,15 267 — безразмерное число, подобное ? или ?2, в том смысле, что его значение не зависит ни от каких человеческих единиц измерения, вроде граммов, метров, секунд или вольт. Почему это значение так близко к 1836? Почему не 2013? Или не 42? Простой ответ состоит в том, что мы этого не знаем. Но, думаю, в принципе мы можем вывести и это число, и все остальные когда-либо измеренные фундаментальные постоянные природы, всего из 32 чисел, перечисленных в табл. 10.1.

Табл. 10.1. Каждое фундаментальное свойство природы, когда-либо подвергнутое измерению, можно вычислить на основе 32 чисел — по крайней мере в принципе. Некоторые из них измерены с очень высокой точностью, тогда как другие экспериментально ещё не определены. Точный смысл этих чисел не имеет значения для нашего изложения, но если вы заинтересовались, то найдёте объяснения в моей статье (http://arxiv.org/abs/astro-ph/0 511 774). Вот только чем определяются значения этих чисел?

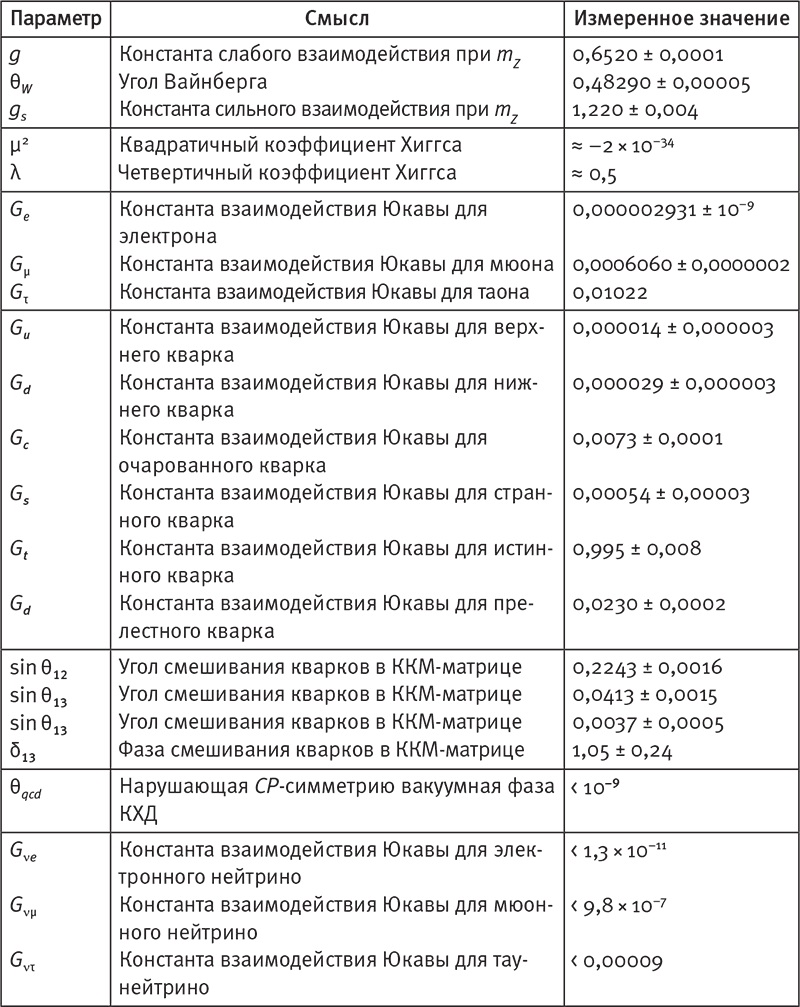
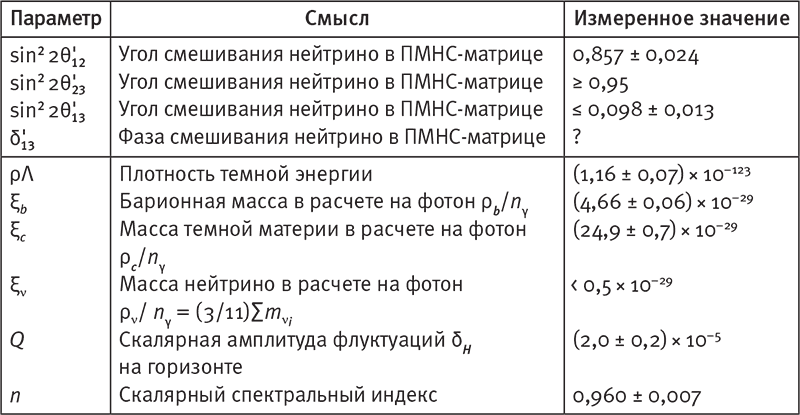
Не пугайтесь названий в таблице: они не имеют отношения к тому, чем мы здесь занимаемся. Суть в том, что в нашей Вселенной есть нечто сугубо математическое, и чем пристальнее мы всматриваемся, тем, похоже, больше математики видим. Что касается природных констант, то имеются сотни тысяч безразмерных чисел, измеренных в разных областях физики: от отношения масс элементарных частиц до отношений характерных длин волн света, испускаемого различными молекулами. С помощью компьютеров, достаточно мощных, чтобы решать уравнения, описывающие законы природы, все до одного эти числа, по-видимому, могут быть определены на основе приведённых в табл. 10.1. Некоторые вычисления и измерения крайне сложны, и их до сих пор не удалось выполнить, а когда удастся, то, возможно, числа в теории и эксперименте не совпадут. Такого рода расхождения не раз случались в прошлом и, как правило, разрешались одним из трёх способов:

В последнем случае обычно удавалось найти более фундаментальные законы физики — как тогда, когда замена ньютоновских уравнений для гравитации эйнштейновскими позволила объяснить, почему Меркурий обращается вокруг Солнца не по идеальному эллипсу. Во всех случаях ощущение, что в природе есть нечто математическое, лишь усиливалось.

Если вы откроете ещё более точные законы физики, то это может либо сделать число параметров менее 32 (табл. 10.1), позволив вычислить некоторые из этих величин по другим, содержащимся в таблице, — либо увеличить их число за счёт добавления новых величин (относящихся, скажем, к массам новых типов частиц, которые, возможно, будут открыты на Большом адронном коллайдере).