Книга: Прикладные аспекты аварийных выбросов в атмосферу

3.8. Высоты подъемов выбросов в атмосфере

3.8. Высоты подъемов выбросов в атмосфере

Как было показано в главе 1, одним из основных параметров в рамках любой математической моде-|ли расчета концентраций загрязняющей примеси является высота вторичного атмосферного источника — фактически высота выброса в месте потери им динамической индивидуальности.

В большинстве современных разработок авторы пытаются использовать аналитические выражения для этого параметра, однако практика применения подобных формул имеет слишком малую область корректного использования в отношении как к тепловой мощности источника, так и к метеопараметрам.

Кроме того, часто путают динамический подъем выбросов с тепловым всплытием их разрушившихся объемов. Ошибочно считают, что тепловой подъем дает искомый результат, после чего наступает фаза атмосферной диффузии.

За границу струи, например, предлагается [136] принять изолинию однопроцентной относительной избыточной температуры.

Не всегда имеются и достаточно точные определения самого понятия подъема выброса. Например, применительно к струям факельного типа за такую высоту принимается [137,138] высоту струи, когда угол касательной к траектории ее наветренной части в сносящем ветре равен 100, в других работах за такую высоту предлагается считать подъем выброса на фиксированном расстоянии от трубы или его подъем за фиксированное время и т. д.

Некоторые авторы считают, что «потолок» выброса достигается, где он еще различим с помощью измерительной или фотографической аппаратуры.

Считается, что в случае когда радиоактивные или химические опасные вещества поступают в атмосферу посредством взрыва, можно пользоваться результатами работы Бриггса [139]. Однако результаты вычислений по приведенным там формулам также имеют весьма ограниченный диапазон применения. Поэтому рекомендуется, если это возможно, эффективную высоту источника загрязнений определять натуральными измерениями или оценкой.

Бриггс в зависимости от метеорологических условий предлагает проводить расчет подъема струи ?h по одной из нескольких модельных формул. Приведем их. Для устойчивого равновесия атмосферы предлагается выражение:

Значения параметра р, входящего в эту формулу, в зависимости от класса устойчивости атмосферы представлены в таблице 3.6.

Таблица № 3.6.

Скоростной параметр р в зависимости от устойчивости атмосферы и типа местности (по данным [162])

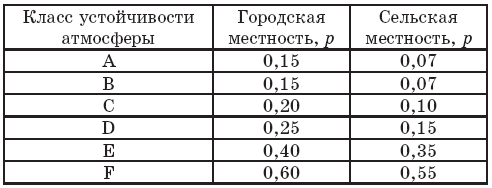
Для высот Z > 200 м следует брать постоянную скорость ветра на высоте 200 м.

Для условий слабых ветров подъема факела на завершающем этапе подъема предлагается находить по формуле:

?h = 5,3 F^1/4 — S^3/8 — R₀,

где R₀ — радиус дымовой трубы.

Для условий, близких к нейтральным, при которых параметр S приближается к нулю, Бриггс предлагает следующую формулу расчета конечного подъема факела:

?h = l,54(F/U SU²_X)^2/3-hs^1/3

где U_х — скорость трения; hs — высота дымовой трубы.

В работе [22] предлагается формула, объединяющая начальный поток количества движения

М₀ = W²₀R²₀ и плавучий поток F:

?h = 3,75M₀^1/2 /U(10 м)+ 5F/U(10 м)³

где U(10 м) — скорости ветра, измеренная на высоте флюгера.

Одной из первых формул, при составлении которой сделана попытка учесть вклад динамического и теплового подъема выброса, является формула Холланда (Holland) [116]:

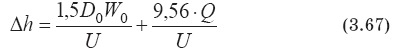
где скорость примеси в выходном сечении W₀ в м/с; диаметр устройства выброса D₀ в метрах.

Эта формула получена в результате обработки наблюдений за шлейфами, выброшенными из трубы на высотах, не превышающих 50 м.

В ряде работ [137], полный подъем выброса в атмосфере предлагается разделить на динамический (газодинамический) ?h_r и тепловой ?h_m — за счет перегрева вещества выброса. Полный подъем загрязняющей примеси ?h при этом определяется сложением динамической и тепловой составляющих:

?h = ?h_m + ?h_r

В частности, для модельных экспериментов для условий тепловых электростанций получены значения ?h_m и ?h_r в следующем виде [157]:

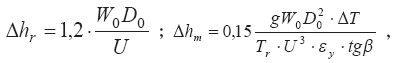
где Т_г — температура отходящих газов;

?Т = Т_r—Т_е;

?_y — интенсивность турбулентности в горизонтальной плоскости; S = 0,05 ? 0,17

? — угол касательной к траектории движения факела; остальные обозначения те же, что и ранее.

Отмечается [137], что если данные по исследованию динамической составляющей подъема факела у разных авторов по характеру влияния на подъем параметров сносящего потока и движущейся в ней струи совпадает, то при изучении тепловой составляющей такое единообразие отсутствует. Оно проявляется в различиях в значениях показателей в формуле для ?h_r, которое приводит к большим отличиям в вычисленных значениях теплового всплытия.

Такое различие вычисляемых ?h_r объясняется

различными теоретическими предпосылками при определении этой характеристики, трудностями исследования теплового подъема на моделях в лабораторных условиях, отсутствием опытных данных по влиянию различных факторов на подъем выброса.

Что касается ограничений для применения аналитических формул, то они не пригодны в случаях сильно стратифицированной атмосферы или при сильном сдвиге ветра.

Рассмотрим теперь некоторые литературные данные по высотам подъемов кратковременных выбросов. По зарубежным литературным источникам, обобщенным в работе [151] для наземных, приземных и воздушных ядерных взрывов высота центра облака после стабилизации может быть найдена по формуле:

h_ц=1070 ·q⁰’²

где q — мощность ядерного заряда;

[q]=T; [h]=M

Модификация этой формулы относительно верхней h_e и нижней h_H границ взрывного облака дает следующие значения:

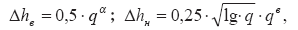
где a = (3 + 0,131gq)^-1; e = (2,6 +0,4lgq)^-1.

Независимая обработка данных по высотам 60 ядерных взрывов привела к появлению формулы, справедливой в диапазоне q от долей тонны до 10⁵т (с надежной статистикой лишь в диапазоне 1-100кт), определяющую высоту подъема h_ц в виде [151]:

h_ц =1600·q^0,21

Для наземных подрывов взрывчатки справедливо соотношение

h_ц = 284·q⁰’²² ·В^-1/3 -0,36u · В^-1, (3.68)

где u — средняя скорость ветра в слое 0·h_ц.

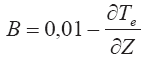
В случае изотермий, когда

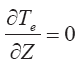
?h_ц = 1400 q^0,22 — 52 (3.69)

Эта формула неприменима при

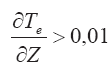
При взрывах химических ВВ в серийных взрывах программы «Хардхет» в умеренноустойчивых условиях высота подъема облака оценивается в следующем виде [151]: h_ц ? 700 qn, (3.70)

где n — принимает значения от 0,2 до 0,25.

Для более полного описания геометрии атмосферного источника при ядерных взрывах целесообразно привести формулы геометрических характеристик подобных источников. Для диаметра облака Д_обл, вертикального его размера ?Н и диаметра «ножки» облака Д_н можно пользоваться следующими оценками:

Д_обл. ⁼ 1600 q⁰’¹¹⁷

?Н = 1430 V⁰’²⁴⁶

Д_н= 1420 V⁰’¹³⁴

Эти же значения параметров, очевидно, могут быть применены для инженерных оценок выбросов при взрывах химических ВВ и авариях взрывного характера на АЭС и других энергоемких объектов. В любом случае после взрыва формируется универсальный по форме атмосферный источник, отличающийся лишь характером поступления примесей и их составом.

В разделе книги, посвященном рассеиванию примесей из вторичных источников, приводится пример, как используя стандартные модели рассеяния, можно получить суммарное поле приземных концентраций в виде суперпозиции концентраций двух источников: облака и «ножки».

Отметим, что приведенные в этом разделе формулы пригодны только для весьма грубых инженерных оценок в соответствующих диапазонах параметров атмосферы и источника загрязнений.

Наилучшие и наиболее корректные результаты в процедуре получения высот подъема выбросов в атмосфере дает, на наш взгляд, решение полной системы дифференциальных уравнений движения выброса при задании пульсационных характеристик атмосферы.

При этом для прерывания расчетного процесса необходимо использовать критерий потери выбросом динамической индивидуальности на фоне пульсационного движения окружающего воздуха.