Книга: Прикладные аспекты аварийных выбросов в атмосферу

3.4. Геометрические характеристики формирующихся кратковременных выбросов

3.4. Геометрические характеристики формирующихся кратковременных выбросов

Формирование кратковременного выброса существенно зависит не только от расходных характеристик

источника загрязнений и атмосферной турбулентности (через коэффициент вовлечения), но и от формы выброса и от площади его поверхности контакта с атмосферным воздухом. Через эту увеличивающуюся поверхность происходит вовлечение окружающей «холодной» среды, которая определяет газодинамические концентрационные и энергетические характеристики вещества выброса. Рассмотрим на примере истечения газа из сопла, как формируются кратковременные выбросы.

Наблюдения за истечением кратковременных струй из сопел показывают, что форма выброса в зависимости от времени работы ракетного двигателя в первые мгновения меняется от части сферы, ограниченной сегментом вращения, до полусферы. Затем форма выброса может хорошо быть смоделирована как суперпозиция усеченного конуса и полусферы. Увеличение временной координаты для неизменных атмосферных условий приводит лишь к изменению масштаба выброса, остающегося практически самоподобным.

Поскольку истечение из ракетных сопел происходит с большими скоростями, то в первом приближении может быть оправданным подход при котором считается формирование полусферического выброса происходящим за первый шаг интегрирования задачи. Далее выброс представляется суммой полусферы и удлиняющегося усеченного конуса (Рис. 3.4).

Для определения координаты центра масс полусферического выброса х_* радиуса R = d₀ (Рис. 3.4а) приравняем массы газа в части выброса при х ? х_* массе газа в части выброса при х > х_*.

Получаем:

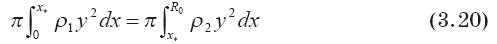
В этом выражении:

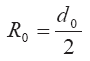
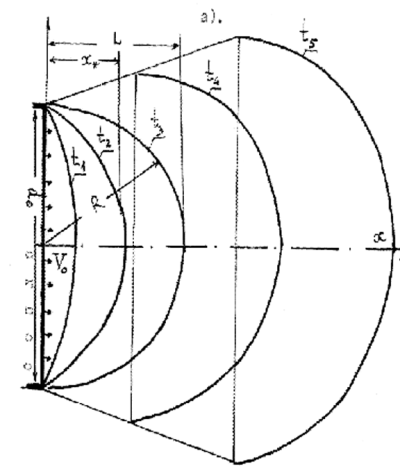
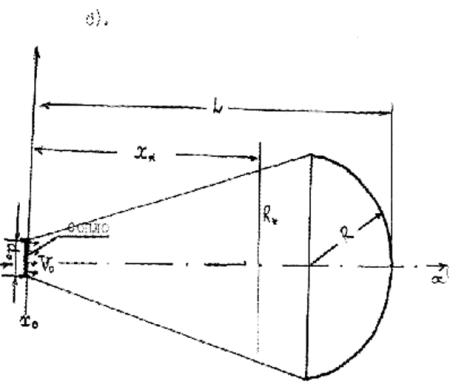
Рис. 3.4. Схема формирования кратковременного выброса при истечении газа из сопла: а) переходный процесс возникновения выброса в окрестности сопла; б) развитый самоподобный выброс.

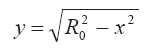
?₁ и ?₂ — плотности газа в левой (х ? х_*) и правой (х > х_*) части выброса, соответственно.

Если предположить, что вещество выброса имеет одинаковую плотность в разных его частях, т. е. ?₁ = ?₂, то приходим к уравнению относительно искомой координаты центра массы х_*. Получаем:

В уравнении (3.21): 

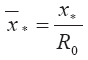
Решением уравнения (3.21) является

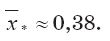
Необходимо отметить, что координата

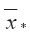
При рассмотрении дальнейшей эволюции выброса координата его центра масс будет функцией угла расширения его конической части, т. е. будет зависеть от турбулентности атмосферы. Для ее нахождения обратимся к Рис. 3.46.

Как следует из него в предложении однородности вещества выброса объем усеченной части выброса до координаты х„должен быть равен сумме объемов остальной части выброса.

Важной характеристикой при расчетах продольной координаты центра масс кратковременного выброса х_* является х_с — координата его центра масс, совпадающая с точкой сопряжения его конической и сферической частей. Важность знания х_с объясняется существенной разницей в форме выброса в зависимости от того, больше или меньше значение текущей продольной координаты значения х_с. Найдем выражение для х_с.

Координаты сопряжения х_с конической части выброса со сферической определяется приравнивания объемов этих частей выброса.

Получаем:

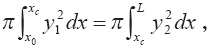
где

у₁ = кх — уравнение образующей конической поверхности выброса;

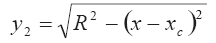
Подставив значения у₁ и у₂ в это соотношение, получаем:

Вещественный корень этого уравнения может быть определен по формуле Кардана [172]:

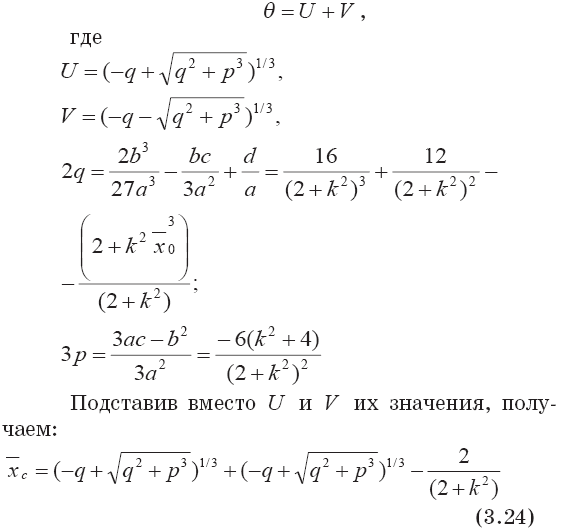
Окончательное выражение для безразмерной продольной координаты сопряжения конической и сферической частей выброса может быть получено при подстановке в соотношение (3.24) вместо р и q их значений. Из-за громоздкости мы его не приводим.

Если известен радиус полусферической «шапки» выброса R, то выражение для продольной координаты сопряжения может быть записано в виде компактного соотношения. Приравниваем объем цилиндрической части выброса

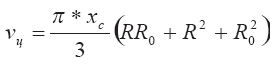
и его сферической части

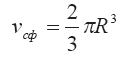
Получаем:

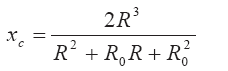
Из рассмотрения Рис. 3.4 видно, что по мере развития выброса координата его центра масс перемещается с полусферической его части на цилиндрическую часть. В математическом виде это утверждение может быть записано так:

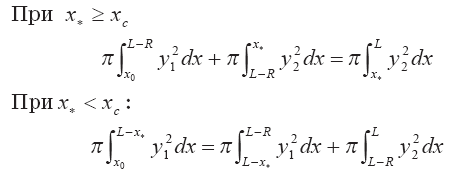
В этих соотношения, как и ранее:

у_х=кх — уравнение цилиндрической образующей конуса;

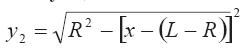
После вычисления интегралов имеем следующие соотношения для определения координаты х_*:

При х_* ? х_с:

v₁ + v₂ = v₃ (3.25)

где

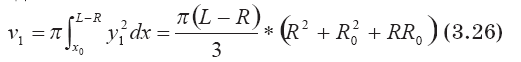
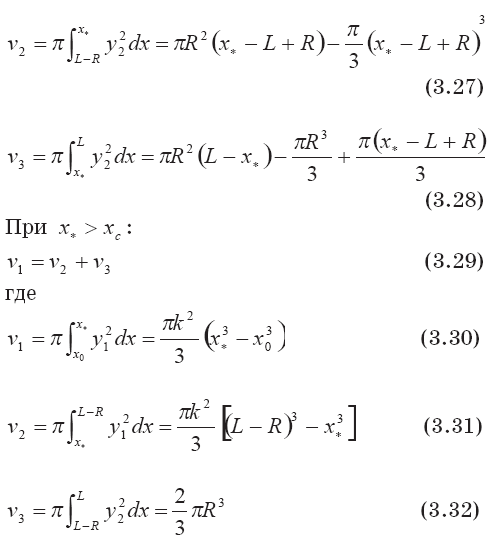
Уравнение (3.25) при учете вида соотношений (3.26), (3.27), (3.28) записывается в виде кубического уравнения

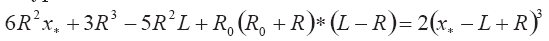
В каноническом виде относительно переменной

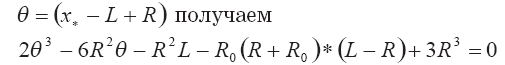
Это уравнение при учете связи характеристик выброса R и L может быть решено аналитически или численно.

Уравнение (3.29) при учете соотношений (3.30), (3.31), (3.32) записывается так:

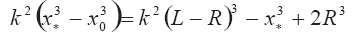
Откуда

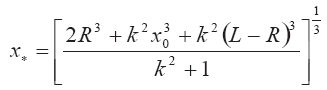
или при учете соотношения

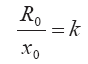
получаем для х_* окончательное выражение (случай х_* <х_с):

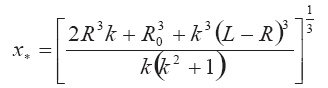
Поперечный размер выброса в месте нахождения его центра масс R„может быть определен при использовании геометрических построений Рис. 3.4.

Здесь, как и ранее, радиус полусферической «шапки» выброса определяется соотношением:

При большом времени истечения вещества из сопла кратковременный выброс перестраивается в струйный. Для струйного выброса значением начального радиуса R₀ можно пренебречь по сравнением с его приращением, т. е.

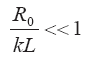
При этом

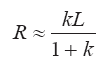
и из соотношения (3.29) при учете (3.30), (3.31) и (3.32) получаем асимптотические зависимости для координат центра масс выброса

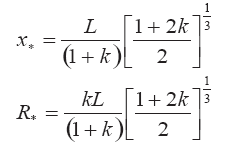
График зависимости безразмерной координаты центра масс струйного выброса 

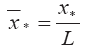
Как следует из графика этого рисунка увеличение угловой координаты его центра масс приводит к линейному уменьшению 

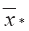
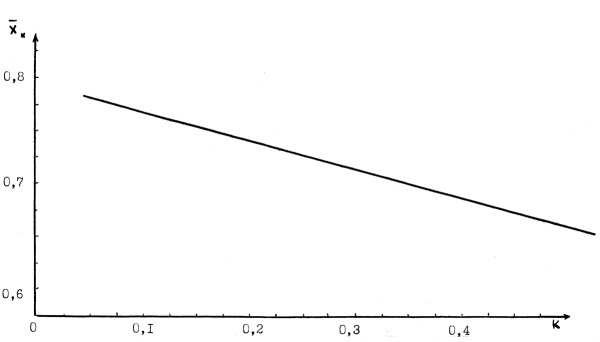
Рис. 3.5. Зависимость безразмерной продольной координаты струйного выброса продуктов горения из сопла от углового коэффициента расширения струи к.

Найдем теперь выражение для поверхностей вовлечения формирующихся кратковременных выбросов. Считаем, что выходящий из сопла газ механически выдавливает окружающий воздух вплоть до полусферического объема (это состояние вещества выброса соответствует временной координате t₃ на Рис. 3.4а). Вовлечение в выброс начинает происходить при t > t₃ через образующуюся коническую его поверхность.

Площадь вовлечения окружающей среды при этом запишется так:

SB = ? (R + R₀) ? L_.обр

где

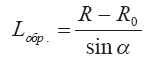
? — угол конической поверхности выброса.

Учитывая связь угла а и коэффициента углового расширения потока к:

к = tg?

находим для образующей следующее L_обр выражение:

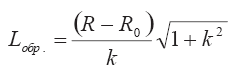
Подставляя в выражение для площади вовлечения вместо L_обр его выражение, получаем:

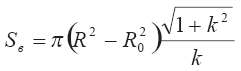
При учете формулы для радиуса R получаем окончательное выражение для поверхности вовлечения кратковременного выброса. Оно имеет вид:

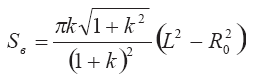
На графике Рис. 3.6 представлена зависимость безразмерной (отнесенной к площади соплового сечения) поверхность вовлечения кратковременного выброса от безразмерной длины выброса для различных значений углового расширения к:

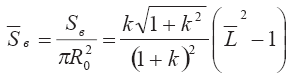
Как следует из этого графика, безразмерная поверхность вовлечения 

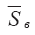
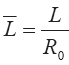
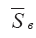
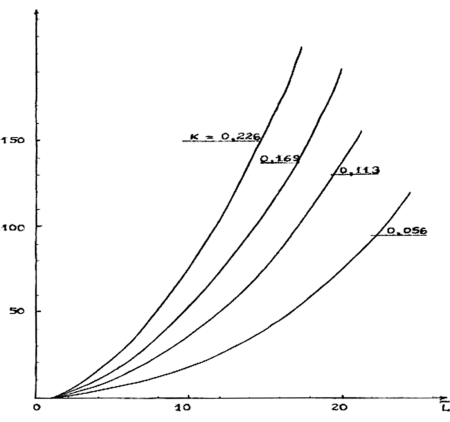
Рис. 3.6. Зависимость безразмерной площади вовлечения в кратковременный выброс от его безразмерной длины для различных значений коэффициента углового расширения потока.

Вычислим теперь объем кратковременного сформировавшегося выброса, состоящего из усеченного конуса и полусферы. Получаем:

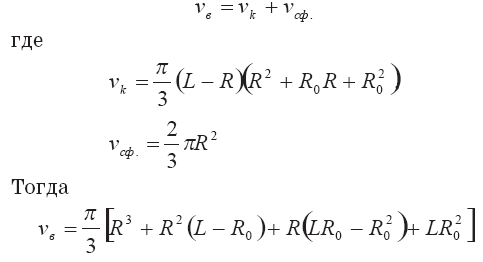
или подставляя вместо R его значение из (3.33), можно получить выражение для объема выброса через его длину и начальный радиус R₀. После громоздких вычислений находим: