Книга: Прикладные аспекты аварийных выбросов в атмосферу

1.3. Математическое моделирование атмосферных выбросов

<<< Назад
 Вперед >>>

1.3. Математическое моделирование атмосферных выбросов

В настоящее время усилиями ученых всего мира создан единый фонд моделей процессов, протекающих в живой и неживой природе. Эти модели, как правило, основываются на небольшом числе фундаментальных принципов, связывающих воедино разнообразные факты и представления естественных |наук. Каждая модель в этом фонде занимает определенное место, установлены пределы ее применимости и связь с другими моделями. Наличие такого фонда моделей придает уверенность исследователям при их использовании в практической деятельности — ведь каждая из этих моделей благодаря связям с другими моделями опирается не столько на специфическую проверку ее самой, сколько на весь практический опыт человечества. Для каждого конкретного объекта в этом фонде можно выбрать наиболее подходящую модель или модифицировать ее из близких по характеру моделей.

Применительно к задачам охраны окружающей среды развитость теорий возникновения и трансформации загрязняющих веществ в природных средах, проявившая себя в наличии грандиозного фонда природных процессов, с одной стороны, определяет высокую эффективность использования математических моделей и методов в инженерной практике, а с другой стороны — дает исследователям единую картину окружающего мира.

В целом основу конструктивного подхода к проблеме взаимодействия человека с природой дает моделирование (в частности, математическое) в сочетании с целенаправленными экспериментальными исследованиями. Загрязнение природных сред — одно из наиболее типичных проявлений такого взаимодействия.

Множество факторов, которое необходимо учитывать в моделях, находится на стыке ряда исследовательских программ [18–23], реализуемых в рамках наук о Земле. Комплексный характер подобных программ и наличие сложных прямых и обратных связей между гидрометеорологическими процессами, загрязнением природных сред, биосферой активно стимулируют разработки теоретических основ и системной организации математических моделей. На этом более высоком уровне системная организация оперирует с «простейшими» моделями как с элементарными объектами.

Применительно к математическому моделированию процессов возникновения и развития в атмосфере аварийных выбросов загрязняющих и токсичных веществ будем исходить из моделей физических процессов. К ним относятся модели гидротермодинамики атмосферы различных пространственно-временных масштабов, а также модели переноса и трансформации примесей, различные способы параметризации и т. п. В литературных источниках имеется достаточно много подобных разработок [21–23]. Их физический смысл и различия между ними зависят от конкретной постановки задач. В любом случае применительно к решению задачи методами численного моделирования исходят из понятий функций состояния и параметров.

Для удобства и краткости изложения воспользуемся операторной формой [19]. Обозначим векторную функцию состояния через 

. К числу ее составляющих относятся поля гидрометеорологических элементов и концентраций загрязняющих примесей.

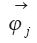
Вектор параметров обозначим

. Параметрами являются коэффициенты уравнений, параметры области интегрирования Dt сеточной области Dht, области размещения наблюдательных систем Dmt , начальные значения функций состояния, распределения и мощности источников тепла, влаги и других примесей и компонентов.

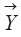
В операторном виде математическая модель описываемого процесса имеет следующий вид:



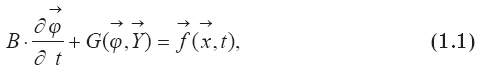
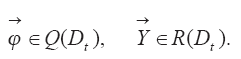
Здесь:


 — нелинейный дифференциальный оператор матричной структуры, действующий на множествах функций 
и 
;

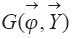
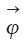
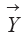
Q(Dt) — пространство функций состояния, удовлетворяющих граничным условиям;

R(Dt) — область допустимых значений параметров;

В — диагональная матрица, в которой все или часть элементов могут быть нулями;


— источники;


 —, где D — область изменения пространственных переменных;


 — интервал изменения времени t.

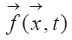
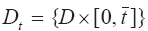
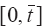
Входящий в соотношение (1.1) оператор

 — определяется уравнениями гидротермодинамики системы атмосфера — почва — вода, переноса и трансформации примесей, а также условиями на границах раздела.

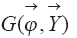
Граничные и начальные условия записываются для конкретного физического содержания модели.

В частности, для математической модели переноса примесей в атмосфере, которая входит в состав уравнения (1.1) в качестве составной части, получаем уравнение


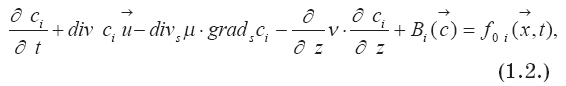
Эта модель учитывает процессы возможной трансформации веществ, турбулентного обмена и обменных процессов между природными средами: водой, воздухом и почвой.

В соотношении (1.2):


 — концентрация примесей;


 — вектор скорости с компонентами u,v,w в направлении пространственных координат 
 соответственно;

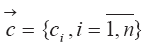
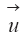
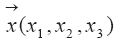
? и ? — коэффициенты турбулентности в горизонтальных (x1,x2) и вертикальном (х3 = z) направлениях;

индексом s отмечены операторы, действующие в горизонтальных направлениях;


 — операторы трансформации примесей;


 — источники примесей (одновременно учитываются источники естественного и антропогенного происхождения).

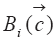
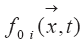
Отметим, что операции с вектором 

реализуются покомпонентно, т. е. уравнение (1.2) представляет собой систему n уравнений в частных производных. Оператор 
— в общем случае нелинейный. Он определяет скорость изменения концентраций ci за счёт химических и фотохимических реакций. Скорости вертикального движения частиц (оседания или всплытия) учитываются функцией w. Примеси — многокомпонентны, количество компонент — входной параметр модели. На практике параметр модели определяется количеством химических веществ, участвующих в реакциях.

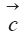
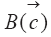
Модель дополняется начальными и граничными условиями:


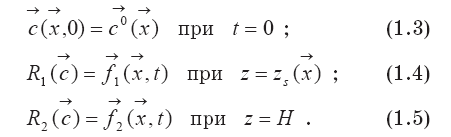
Здесь:

R1 и R 2 — некоторые операторы;


 — источники и стоки примесей на верхней и нижней границах области D.

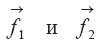
Для глобальной модели задаются условия периодичности всех функций на поверхности сферы, а для моделей на ограниченной территории — условия на поля концентраций на боковых границах области Dt.

Процессы взаимодействия примесей с подстилающей поверхностью, включая обменные процессы между воздухом, водой, почвой и растительностью, описываются оператором

. Причем вектор концентраций 
включается в вектор-функцию состояния системы в целом, а коэффициенты уравнений (1.2) и граничных условий (1.4), (1.5), а также начальные условия (1.3), функции источников
 и константы скоростей газофазных реакций в операторе 
включаются в вектор параметров.

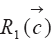
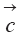
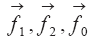
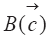
Отметим, что в вычислительных моделях [19] используется расширительное понятие параметров, включая в их число не только численные значения некоторых величин, но и алгоритмы их вычисления. Тогда в число параметров попадают схемы реакций, алгоритмы вычислений радиационных потоков тепла, коэффициентов турбулентного обмена, а также коэффициентов в моделях взаимодействия воздушных масс с подстилающей поверхностью.

Развитием представленных здесь подходов для построения дискретных аналогов моделей и вычислительных алгоритмов применяются вариационные принципы [19], использование которых дает качественно новую информацию о поведении математической модели.

Очевидно, что в процессе численного моделирования не должен потеряться смысл, заложенный в исходных постановках задачи, а результаты вычислений должны соответствовать реально протекающим процессам.

При решении практических задач всегда остро стоит проблема задания входных параметров и начальных данных, информация о которых, как правило, является отрывочной и неполной. Поэтому использование многомерных и многокомпонентных моделей, создавая иллюзию детального рассмотрения процесса, не способно выдать результаты, точность которых превышает точность исходных постановочных параметров. Каждая математическая модель только тогда может считаться состоявшейся, когда проведена оценка достоверности результатов ее использования.

<<< Назад
 Вперед >>>
Оглавление статьи/книги
Похожие страницы

Генерация: 4.986. Запросов К БД/Cache: 3 / 1
Вверх Вниз