Книга: История астрономии. Великие открытия с древности до Средневековья

Глава 15 Кеплер

Глава 15

Кеплер

В январе 1599 года Местлин, услышав от своего бывшего ученика Иоганна Кеплера о трудностях, с которыми столкнулся Тихо Браге при определении эксцентриситетов планет, написал в ответ, что Браге оставил только тень от того, что раньше считалось астрономической наукой, и что теперь известно лишь одно: человечество ничего не знает об астрономии.

Великий астроном-практик действительно во всей полноте показал недостатки предыдущих теорий, но в то же время настолько увеличил точность наблюдений за положениями небесных тел, что создал возможность для создания удовлетворительной теории и, что еще лучше, для определения фактических орбит в пространстве, по которым движутся все планеты, чего до той поры не удавалось достигнуть никому. Благодаря Тихо Браге материал для изучения был готов, был готов и математик, который смог им воспользоваться; и это был тот самый человек, которому Местлин адресовал те отчаянные слова и который уже выступил с весьма многообещающим дебютом в научном мире.

Кеплер родился 27 декабря 1571 года в Вюртемберге и с 1589 года учился в Тюбингенском университете, где через Местлина познакомился с учением Коперника и убедился, что оно представляет собой истинную систему мироздания. Первоначально он собирался стать священником, но, так как лютеранская церковь или, скорее, чрезвычайная узость мышления, преобладавшая среди ее служителей, не пришлась ему по вкусу, в 1594 году он поступил на должность «математика провинции» в Штирии и с тех пор посвятил жизнь науке. Уже в 1596 году свет увидела его первая крупная работа, которую он, чувствуя, что это всего лишь предтеча других, еще более великих трудов, озаглавил Prodromus dissertationum cosmogra-phicarum continens mysterium cosmographicum, «Предвестник космологических сочинений, содержащий тайны мироздания». Хотя книга не раскрывает тайн устройства планетных орбит, как от души надеялся ее автор, она тем не менее содержит первое великое открытие Кеплера. Причины отказа от птолемеевской системы в пользу коперниковской излагаются в первой главе с изумительной ясностью. На двух весьма наглядных чертежах он показывает, что птолемеевские эпициклы внешних планет с Земли видны точно под тем же самым углом, что и орбита Земли с точки на орбите каждой внешней планеты, а далее он демонстрирует, что это объясняет, почему у Марса такой огромный эпицикл, хотя у Юпитера эпицикл намного меньше, а у Сатурна и того меньше, притом что их эксцентры гораздо больше, чем у Марса. Птолемеевская система не могла объяснить причин ни такого причудливого устройства, ни того странного факта, что три планеты во время противостояния с Солнцем должны находиться на перигеях своих эпициклов. Также она не могла ни показать, почему периоды внутренних планет на их эксцентрах обязательно должны быть равны периоду Солнца, ни привести причин, почему Солнце и Луна никогда не совершают попятного движения. Все эти факты изумительно просто объясняются учением о годовом движении Земли, причем Коперник к тому же смог объяснить прецессию, не привлекая «той чудовищно громадной беззвездной девятой сферы альфонсинцев». Поистине невозможно понять, как можно было после прочтения этой главы оставаться приверженцем системы Птолемея.

Чего добивался Кеплер всю свою жизнь, так это найти тот закон, который связывает воедино тела Солнечной системы, применительно к расположению их орбит в пространстве и их движений, и он надеялся, что овладение этим законом позволит рассчитать все детали для любой планеты при условии, что известны элементы одной орбиты. Первая порция фактов содержится в Mysterium cosmographicum, «Тайне мироздания», которая рассматривает проблему нахождения закона, связывающего относительные расстояния планет. В предисловии он говорит читателю, как пришел к этому открытию, которое он полагает великим. Кеплер был убежден, что должна существовать какая-то причина, почему количество, расстояния и скорости движущихся небесных тел имеют именно те значения, которые следуют из наблюдений; и надежда найти ее основывалась на том, что неподвижные тела – Солнце, звезды и промежуточное пространство – соответствуют Богу Отцу, Богу Сыну и Святому Духу. Он пробовал установить, не может ли быть так, что одна сфера в два, три, четыре раза больше, чем другая; он пробовал поместить планету между Марсом и Юпитером и еще одну между Меркурием и Венерой (допустим, если она слишком мала, чтобы ее можно было увидеть), а когда ему даже не удалось найти простого отношения между расстояниями от Солнца, он попытался найти какую-нибудь тригонометрическую функцию, определяющую это отношение. Случайность в конце концов позволила ему найти закон расстояний в геометрии. Во время лекции (9/19 июля 1595 года) Кеплер описывал циклы великих соединений планет и то, как соединения переходят из одного «тритона» зодиака в другой, и схема, которую он начертил для иллюстрации, напомнила ему о пяти правильных геометрических телах, и его осенило, что именно им, а не плоским фигурам подобает описывать отношения между космическими сферами (inter solidos orbes). Между шестью планетными сферами есть пять интервалов, и, приняв приведенные Коперником значения полудиаметров сфер, Кеплер обнаружил, что между сферами в следующем порядке помещаются пять геометрических тел:

Сатурн,

куб,

Юпитер,

тетраэдр,

Марс,

додекаэдр,

Земля,

икосаэдр,

Венера,

октаэдр,

Меркурий.

Сфера Сатурна описывает куб, в который вписана сфера Юпитера; та, в свою очередь, описывает тетраэдр, и так далее. Но так как орбиты планет являются не концентрическими, а эксцентрическими кругами, возникла необходимость (у арабов и Пурбаха) придать каждой сфере толщину, достаточную для вмещения эксцентрической орбиты между внутренней и внешней поверхностью. В Средние века, как мы уже видели, существовала гипотеза, что внешняя поверхность одной сферы касается внутренней поверхности другой, ближайшей к ней, потому что система Птолемея не давала ни малейшего представления об относительных расстояниях планет. Однако система Коперника не позволяет произвольно выбрать размеры сфер, это заданные величины, оставляющие достаточно места между сферами. Поэтому встал вопрос: насколько размеры сфер, производные из расстояний и эксцентриситетов по Копернику, укладываются в вычисленные таким образом размеры пяти правильных тел, так чтобы внутренняя поверхность сферы совпадала со сферой, описанной вокруг следующего ниже тела, а внешняя поверхность – со сферой, вписанной в тело, следующее выше? В нижеследующей таблице показаны результаты вычислений Кеплера[335]:

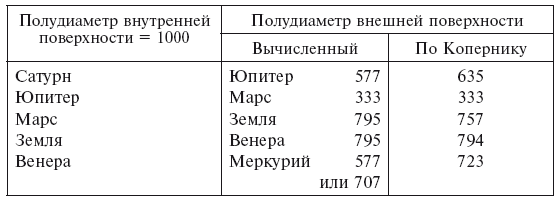
Второе значение для Меркурия – это полудиаметр окружности, вписанной в квадрат, образованный четырьмя средними сторонами октаэдра. Если толщину земной сферы увеличить за счет включения лунной орбиты, цифры в последнем столбце становятся: 847 для Венеры и 801 для Земли. Совпадение между вычисленными значениями и значениями по Копернику вполне удовлетворительное, за исключением Юпитера, «чему не следует удивляться, учитывая огромное расстояние». Кеплер добавляет, что легко понять, насколько велика была бы разница, если бы схема противоречила природе небес, то есть если бы Бог в момент творения не имел в виду эти пропорции, ведь такое не может быть случайным. У всего должна быть причина, и Кеплер готов объяснить, почему пять правильных тел расположены именно в таком порядке. Они относятся к двум видам: первичному (куб, тетраэдр, додекаэдр) и вторичному (икосаэдр и октаэдр), которые во многом отличаются друг от друга. Земля, будучи жилищем человека, созданного по образу Божьему, достойна быть помещенной между двумя этими видами тел; куб является внешним, потому что он самый важный, так как единственный образован собственным основанием и своими углами указывает на три пространственных измерения. Для порядка других тел он приводит множество причин, одну фантастичнее другой. Но нам придется пропустить все эти любопытные детали, как и девятую главу, в которой из природы пяти геометрических тел выводятся астрологические свойства пяти планет.

Хотя кеплеровская разгадка «тайны мироздания» оказалась неверной, для него было вполне естественно начать эту работу с поисков каких-либо отношений между расстояниями планет от Солнца, и довольно странно, что он не наткнулся на последовательность, ошибочно называемую правилом Тициуса—Боде. Быть может, он смог бы ее найти, если бы сразу же не увлекся пятью телами и всю свою жизнь оставался верен своей первой небесной любви[336].

Совпадение между теорией и числовыми данными Коперника было неидеальным, и тогда перед Кеплером встал вопрос, как его улучшить. Он напоминает читателю, что труд Коперника не космографический, а астрономический, то есть для него не имело особого значения, если он слегка заблуждался относительно истинного соотношения сфер, при условии что с помощью одних только наблюдений он мог найти цифры, подходящие для вычисления движений и расположения планет. Поэтому ничто не мешает кому-то исправить его цифры, если только он не станет вносить больших или вообще любых изменений в уравнения времени. Что главным образом интересовало Кеплера в предпринятом им исследовании, это эксцентриситеты, от которых зависела толщина сфер. Тогда его озарило, что, хотя Коперник, вне всякого сомнения, поместил Солнце в центре Вселенной, все же «в качестве вспомогательного средства для расчета и чтобы не запутывать читателя слишком далеким отходом от Птолемея» он относил все не к центру Солнца, а к центру орбиты Земли. Следовательно, через эту точку в теории Коперника проходят не только линии узлов каждой планеты, но и линии апсид, так что эксцентриситеты отсчитываются от точки, расстояние которой от Солнца определяет размер эксцентриситета Земли. То есть следовать Копернику в этом вопросе означает не придавать Земле эксцентриситета и ее сфере – толщины, так что центры граней додекаэдра и вершины икосаэдра падают на ту же сферическую поверхность, уменьшая размеры системы более, чем позволяют наблюдения. Кеплер связался с Местлином, который охотно взялся за расчет изменений, которые повлечет за собой установление Солнца в качестве центра в данных Коперника. Естественно, что изменения оказались весьма значительными; так, было установлено, что долгота афелия Венеры отличается примерно на три знака зодиака (90°) от апогея, в то время как новое расстояние Сатурна отличается от старого на всю величину эксцентриситета Земли.

Затем Кеплер приводит таблицу годовых параллаксов планет в афелии, сначала (1) рассчитанных по его теории, исключая лунную орбиту из земной сферы, затем (2) согласно расстояниям от Солнца (Коперник) и, наконец, (3) рассчитанных по его теории с увеличением сферы Земли за счет лунной орбиты. Различия оказались весьма существенными[337], и положения планет, рассчитанные по новой теории, значительно отличаются от рассчитанных по «Прусским таблицам». Но это не заставляет Кеплера усомниться в истинности его теории. В мастерски написанной второй главе он рассматривает недостатки теории Коперника и «Прусских таблиц», которые часто на несколько градусов отличались от наблюдаемых положений планет, и, в частности, показывает, что эксцентриситеты, указанные Коперником, не имеют ценности. Коперник полагал, что эксцентриситеты Марса и Венеры изменились, тогда как, если отнести их к Солнцу, оказалось, что они не меняются. Местлин обратил внимание Кеплера на слова Коперника, о которых сообщил Ретик, которые показывали, насколько глубоко великий мастер осознавал недостаточность данных, на которых ему приходилось основывать свои построения, и он объяснял ее тремя причинами: во-первых, некоторые наблюдения древних приведены недобросовестно и изменены так, чтобы укладываться в их теории; во-вторых, ошибки в расположении звезд у древних могут достигать 10?; и, в-третьих, не сохранилось сравнительно недавних наблюдений, подобных тем, которыми располагал Птолемей. Поэтому Кеплер спокойно ждал, когда астрономы вынесут свое суждение.

Наконец, Кеплер отважился на попытку найти «пропорции движений относительно орбит». Так как периоды обращения непропорциональны расстояниям до Солнца, мы должны либо предположить, что «animae motrices»[338], более удаленные от Солнца, слабее, либо что есть только одна anima motrix в центре всех орбит, а именно Солнце, которое более сильно действует на тела, расположенные ближе, нежели на расположенные дальше. Он отдает предпочтение второму допущению. Он полагает вероятным, что эта сила обратно пропорциональна кругу, по которому должна распределяться, и уменьшается по мере увеличения расстояния. В то же время период увеличивается с длиной окружности, «следовательно, большее расстояние от Солнца действует дважды на увеличение периода и, наоборот, половина увеличения периода пропорциональна увеличению расстояния». Например, период Меркурия составляет 88 дней, а Венеры – 224? дня, так что половина увеличения периода равна 68?; следовательно, 88 : 156? : : расстояние Меркурия : расстояние Венеры. Начиная от Сатурна, Кеплер находит следующие отношения расстояний:

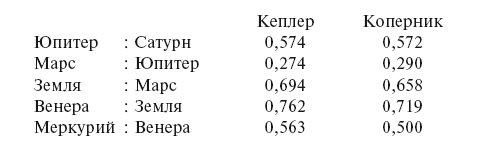
«Мы приблизились к истине», – говорит Кеплер. Но пройдет еще двадцать два года, прежде чем он найдет истинный закон. Интересно отметить, что еще в 1596 году он распознал, что движением планет должна управлять или вызывать его сила, исходящая от Солнца, и что уже тогда он сделал ошибочное предположение, от которого так и не отказался, что действие этой силы обратно пропорционально расстоянию от Солнца.

Хотя главная идея «Тайны мироздания» была ошибочной, невозможно передать, насколько мы обязаны этому труду, так как он представляет собой первый шаг к очищению системы Коперника от пережитков птолемеевской теории, за которую она по-прежнему цеплялась. Величайшим желанием Кеплера теперь стало получить более точные значения средних расстояний и эксцентриситетов, чтобы доказать абсолютную истинность его теории, и единственным местом в мире, где он мог получить такую информацию, была обсерватория Тихо Браге. Большое расстояние, отделявшее Грац от Дании, могло помешать Кеплеру отправиться к Браге на его остров, но, к счастью для научного прогресса, Браге, поссорившись со многими влиятельными людьми в Дании и, может быть, боясь, что его великое сокровище наблюдений могут забрать у него под тем предлогом, что они были сделаны за государственный счет и потому принадлежат государству, уехал из Дании в 1597 году и два года спустя поселился в Богемии. Вынужденный покинуть Штирию из-за религиозных гонений, Кеплер приехал в Прагу в январе 1600 года и в следующем году был назначен сотрудником к Браге, а в октябре 1601 года стал его преемником на посту императорского математика. Хотя вплоть до августа 1601 года ему приходилось часто отвлекаться от работу из-за поездок в Штирию по личным делам и болезни, вскоре он добился хорошего прогресса в изучении движений самой беспокойной планеты.

Когда Кеплер в феврале 1600 года присоединился к Браге в замке Бенатки, Марс недавно вышел из противостояния с Солнцем, была подготовлена таблица противостояний, наблюдавшихся с 1580 года, и разработана теория, которая очень хорошо отображала долготы в противостоянии, а остальные ошибки составили не более 2?[339]. Но теория не могла отобразить широты и годовые параллаксы, и Кеплер стал задумываться, не оказалась ли она в конце концов ошибочной, даже если и представляла долготу в противостоянии с такой точностью. Несколько частностей в теории вызывали возражения у Кеплера. В первую очередь Браге, как и Коперник, определял движение планет относительно среднего положения Солнца. Кеплер отверг этот принцип в своей книге, так как он предполагает движение вокруг математической точки, а не вокруг огромного тела Солнца. Но этот принцип вызывает возражение и с практической точки зрения. Из наблюдений во время противостояния было вычислено время, когда Марс на 180° отходит от средней долготы Солнца, и, значит, движение Солнца (или, вернее, Земли) следовало считать известной величиной. Поэтому в какой-то степени большое преимущество использования противостояний (что наблюдаемые долготы равны гелиоцентрическим долготам) сходило на нет, и «первое неравенство» не определялось независимо от «второго», вызванного движением Земли или, в системе Браге, Солнца. В случае Марса долгота в «среднем противостоянии» могла отличаться более чем на 5° от долготы в фактическом противостоянии – весьма серьезное расхождение. В конце концов Кеплеру удалось убедить Браге и Лонгомонтана принять видимое положение Солнца для теории Луны, тогда как его собственное длительное исследование Марса все больше и больше внушало ему необходимость определять движение планеты относительно истинного положения Солнца. Другое возражение Кеплера против теории Марса Браге состояло в том, что годовая орбита Солнца предполагалась простым эксцентрическим кругом (как в теории Птолемея и Коперника) с эксцентриситетом равным 0,035 84. В «Тайне мироздания» Кеплер высказался в том смысле, что когда-нибудь будет установлено, что все планеты, в том числе Земля, движутся совершенно одинаковым образом. Теперь же он указал Браге на то, что видимое попеременное сокращение и расширение годовой орбиты Земли (или Солнца), которое установил Браге в 1591 году, вызвано тем простым фактом, что движение на этой орбите неоднородно по отношению к центру, но по отношению к точке экванта – точно такое, как в планетных теориях Птолемея. В данном случае легко увидеть, что годовой параллакс, или разница между гелиоцентрической и геоцентрической долготой планеты, будет меняться в зависимости от ее положения относительно линии апсид Земли. Если Марс находится на продолжении этой линии и наблюдается с двух точек на равных расстояниях по обе стороны от линии, то параллаксы будут равны, независимо от того, где на этой линии расположена точка экванта. Но если Марс находится примерно в 90° от апсид Земли и наблюдается из апсид или с двух точек в средних аномалиях а и 180° – а, параллаксы не будут равны, если только точка экванта не находится в центре орбиты, но будут отличаться в большей или меньшей степени в зависимости от того, ближе или дальше Земля от апсид. Браге, видимо, подозревал, что это и есть истинное объяснение странного явления, но, так как он хотел, чтобы его книга (Progymnasmata) все-таки увидела свет без очередных задержек, он не ввел в нее бисекцию солнечного эксцентриситета, и Кеплер лишь упоминает об этом в приложении, которым закончил книгу уже после смерти Тихо Браге.

Тихо Браге умер 24 октября 1601 года и на смертном одре попросил Кеплера продолжить реформу теоретической астрономии, которую он обдумывал, на основе его геогелиоцентрической системы, а не коперниковской. Хотя реформаторские усилия Кеплера в конечном итоге привели лишь к окончательному утверждению системы Коперника, все же он добросовестно продемонстрировал теорию Марса в соответствии с тремя системами: Птолемея, Браге и Коперника, помня последнее желание великого астронома-практика, чье удивительное предвидение обеспечило неисчерпаемый кладезь наблюдений, сделанных во всех мыслимых условиях. Еще до смерти Браге Кеплер добился существенного прогресса в работе о Марсе[340], а четыре года спустя она была закончена. С этого момента мы будем следить за его исследованиями в том порядке, в котором он сам их зафиксировал.

Для начала показав, что из наблюдений Браге нельзя сделать никаких определенных выводов относительно горизонтального параллакса Марса, за исключением того, что он не превышает 4?, а вероятно, гораздо меньше, Кеплер далее находит те элементы орбиты, которые можно определить отдельно. Долготу восходящего узла он установил, перерыв бумаги Браге в поисках наблюдений планеты в моменты, когда у нее не было широты, и затем рассчитал ее гелиоцентрическую долготу по теории Браге. Шесть наблюдений такого рода дали ему долготу восходящего узла, равную 46?°. Далее он тремя методами определил наклон орбиты к плоскости эклиптики. Во-первых, выбрав наблюдения Марса в 90° от узлов, сделанные в момент, когда расстояние от Земли до Марса равно расстоянию от Марса до Солнца, в то время как наблюдаемая широта равна наклону. Во-вторых, взяв планету в тот момент, когда она находится в квадратуре к Солнцу, а Земля и Солнце находятся на линии узлов; наблюдаемая широта при этом опять-таки равна наклону. В-третьих, по методу Коперника, воспользовавшись широтами, наблюдаемыми в момент противостояния. Первый и третий способ предполагают, что отношение размеров орбит известно, тогда как второй метод совершенно не зависит от какой-либо прежней теории, и Кеплеру удалось найти четыре наблюдения, удовлетворяющие условиям второго способа. Этими способами он нашел наклон равным 1°50? и доказал, что плоскость орбиты проходит через Солнце и что наклон является постоянным, так что колебания орбиты, до той поры считавшиеся необходимыми, в действительности не существуют. Именно тогда, провозгласив это важное открытие, он и сказал те слова, что Коперник сам не осознавал открытых им богатств.

Следующим и самым важным шагом было определение положения линии апсид (долготы афелия), эксцентриситета и средней аномалии в ту или иную дату. Для определения этих трех величин Птолемею требовались только три противостояния, так как он исходил из бисекции эксцентриситета (на рисунке CA = CS), но, так как Кеплер твердо решил, следуя за Коперником и Браге, не делать подобных допущений, ему пришлось использовать четыре противостояния. Из десяти противостояний, наблюдавшихся Браге (к которым он смог добавить еще два, которые наблюдал сам в 1602 и 1604 годах), он выбрал относящиеся к 1587, 1591, 1593 и 1595 годам и вывел из них время истинного противостояния.

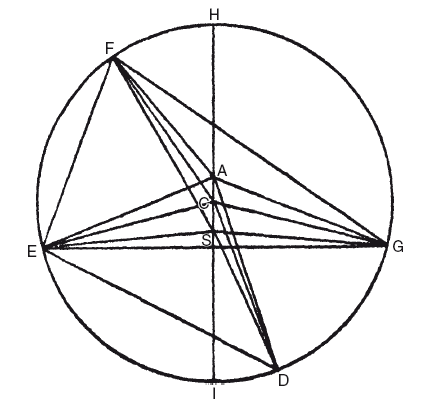
На рисунке D, G, F, E – это четыре наблюдаемых положения Марса, S – Солнце, G – центр круговой орбиты, A – точка экванта, HI – линия апсид. Положение этой линии и средняя аномалия первого противостояния, то есть углы HSF и HAF, в первом примере заимствованы из теории Браге. Наблюдения дали непосредственно гелиоцентрические долготы, то есть углы при S между линиями SF, SE, SD и SG, тогда как углы при A, разности средней аномалии, были известны, так как период сидерического обращения давал среднее движение. Из треугольников ASF, ASE, ASD и ASG, в которых углы при AS известны, далее рассчитываются расстояния SF, SE, SD и SG, выраженные в частях AS. Из треугольников SFE и SFG находится угол F четырехугольника FEDG и аналогичным образом три других угла E, D, G. Если теперь четыре точки F, E, D, G лежат на окружности круга, у нас должно быть

F+ D = G + Е = 180°.

Когда это условие выполняется, нужно найти, находится ли центр круга на линии AS. В треугольнике SFG мы можем посчитать длину FG, так как мы знаем угол при S и другие две стороны; в равнобедренном треугольнике FCG мы теперь знаем FG и угол FCG, причем последний равен удвоенному FEG (или удвоенной сумме FES и SEG), значит, мы можем найти два радиуса в частях AS и угол CFG. Далее, угол SFO = SFG – CFG, следовательно, мы в треугольнике CSF мы можем найти сторону CS и угол CSF, и у нас должно получиться

GSF = HSF.

Поэтому необходимо изменить предполагаемое направление Ш или углы HSF и HAF (истинная и средняя аномалия первого противостояния) так, чтобы выполнялись оба условия, то есть пока четыре точки не будут лежать на круге, центр которого находится на линии, соединяющей S и А.

Кеплер верно говорит, что, если читатель находит это описание метода утомительным, ему следует пожалеть автора, который проверил его не меньше семидесяти раз, и ему не следует удивляться, что Марс потребовал более пяти лет, хотя почти целый 1603 год был потрачен на оптические исследования. Результатом семидесяти этих попыток стала (радиус круга = 1)

Долгота афелия 28°48?55? Льва[341] (1587 г.)

АС = 0,072 32 CS= 0,113 32.

Эту теорию Кеплер впоследствии назвал «заместительной гипотезой». Она очень хорошо отображала долготы двенадцати противостояний, и наибольшая остаточная ошибка составляла 2?12?, которая, как полагал Кеплер, происходила в основном из-за ошибок наблюдений, так как видимый диаметр Марса в ближайшем к Земле положении казался весьма значительным. И все же теория оказалась ложной, и Кеплер полагал, что, когда Птолемей допустил бисекцию эксцентриситета (АС = CS), он должен был встретиться с аналогичной трудностью, которая, вероятно, заставила и Браге отложить в сторону теорию Марса и заняться вместо нее теорией Луны. Кеплер проверил теорию на широтах противостояний 1585 и 1593 годов, когда Марс находился вблизи пределов наибольшей северной и южной широты и в то же время вблизи афелия и перигелия. Применив солнечную теорию Браге без изменений, он обнаружил, что эксцентриситет получится = 0,080 00 или = 0,099 43, в зависимости от того, что использовалось – истинное или среднее противостояние, и результат очень отличается от 0,113 32, но не очень от ? (АС + CS) = 0,092 82. Поэтому он попробовал, что будет, если принять АС = CS = 0,092 82, но это оказалось неудачным шагом, так как, хотя места примерно в 90° от апсид были хорошо представлены, места в аномалиях 45°, 135° и т. д. отличались примерно на 8?. Теперь понятно, говорит Кеплер, почему Птолемей закрыл глаза на бисекцию эксцентриситета, так как 8? вполне укладывались в пределы точности его наблюдений (10?); но Божья благодать одарила нас самым добросовестным наблюдателем в лице Тихо Браге, и потому мы должны с благодарностью использовать этот дар, чтобы найти истинные движения небесных тел. Еще одно доказательство ошибочности «заместительной гипотезы» предоставило исследование долгот вне противостояний, но вблизи апсид. Они также дали эксцентриситет около 0,09. Таким образом, заместительная гипотеза, которая стоила такого огромного труда, окончилась полным провалом. И это показало, что либо орбита представляет собой не круг, либо, если это все же круг, внутри его нет неподвижной точки, при взгляде из которой планета перемещается равномерно, но что точка экванта должна колебаться взад-вперед по линии апсид, что не могло быть следствием какой-либо естественной причины.

Доказав таким образом невозможность создания правильной теории на одних противостояниях, Кеплер осознал, что проблему надо решать в более общем виде, а не разбираться с первым и вторым неравенствами по отдельности, как поступали его предшественники. Он решил взяться сначала за второе неравенство путем более строгого изучения годовой орбиты Земли. В «Тайне мироздания» он попытался объяснить, что планета движется быстрее всего в перигелии и медленнее всего в афелии, потому что в этих точках она ближе всего к Солнцу и наиболее удалена от него, и поэтому, соответственно, находится под наибольшим и наименьшим влиянием некой исходящей от Солнца силы. Но он признал, что если бы это объяснение было правильным, то Земля должна была бы двигаться точно таким же образом, как планеты, но все же никто не приписывал экванты годовой орбите и не представлял ее какой-либо иной формы, кроме простого эксцентрического круга. Поэтому Кеплер испытал настоящее счастье, когда его озарило (dictabat mihi genius, как он говорит), что видимое изменение диаметра годовой орбиты должно вызываться тем, что центр равных расстояний и центр равного углового движения совпадали у Земли не больше, чем у орбит планет. Но теперь это следовало строго доказать.

Доказав сначала реальность предполагаемого явления с помощью двух наблюдений Марса в той же гелиоцентрической долготе, сделанных в те моменты, когда разницы гелиоцентрических долгот планеты и Земли были равны, показав, что параллаксы вместо того, чтобы быть равными, отличаются на 1°14,5?, Кеплер определил эксцентриситет орбиты Земли с помощью наблюдений Марса в одной точке его орбиты, сделанных из нескольких точек орбиты Земли. В треугольнике между Солнцем (S), Землей (Е) и проекцией Марса на плоскости эклиптики (М) углы при S и Е известны, гелиоцентрическая долгота Марса взята либо у Браге, либо из заместительной теории; из них было найдено отношение сторон SE к SM. Аналогичным образом можно было установить отношение других радиус-векторов к SM, выбрав другие наблюдения Марса, сделанные по прошествии ровно одного или нескольких периодов сидерического обращения, и тогда нахождение радиуса круга, расстояния до S от центра и направления диаметра через S, то есть линии апсид, превращалось в простую геометрическую задачу. Из тех же наблюдений и таким же образом он определил расстояние от точки экванта до центра круга, и это расстояние, как и расстояние до Солнца от центра, было найдено равным приблизительно 0,018 00 (радиус = 1), или почти половине эксцентриситета Браге, так что уверенное подозрение Кеплера, что его следует разделить надвое и что Земля вращается точно по тем же принципам, что и планеты, полностью подтвердилось[342]. Меньшее значение эксцентриситета прекрасно согласовалось с очень малым изменением видимого диаметра Солнца в течение года, при этом обнаружилось, что разница между уравнением центра, вычисленного по старой и новой теории, оказалась незначительной и составила не более чем несколько секунд.

Подтверждение идеи Кеплера о сходстве движения Земли и планет естественно побудило его вернуться к гипотезе, высказанной в «Тайне мироздания», что это движение вызывает некая исходящая от Солнца сила; и так как действие подобной силы непременно должно так или иначе изменяться с изменением расстояния до Солнца, он пришел к мысли о переменной скорости планеты на протяжении всей ее орбиты. Таким образом, в конце концов Кеплеру удалось избавиться от птолемеевского экванта и заменить его законом, который впоследствии стал известен как второй закон Кеплера, хотя в действительности он был открыт первым. Поскольку орбиты планет расположены практически в одной плоскости, то есть плоскости эклиптики, Кеплер предположил, что сила (virtus) действует только в плоскости орбит и, следовательно, просто обратно пропорциональна расстоянию. То же самое имеет место с орбитальной скоростью, и, значит, небольшое время, за которое планета проходит по очень малой дуге орбиты, пропорционально радиус-вектору. Кеплер доказывает это для окрестности апсид в птолемеевском эксцентрическом круге и без дальнейших изысканий предполагает, что это верно для любой точки орбиты; и даже позже, признав, что орбиты имеют эллиптическую форму, он продолжал считать доказательство верным как нечто само собой разумеющееся. Сейчас нам известно, что в этом он был не прав, так как скорость в любой точке пропорциональна перпендикуляру из фокуса к касательной в рассматриваемой точке, так что теорема Кеплера верна только для апсид, где радиус-вектор перпендикулярен касательной. Но изъян в рассуждениях Кеплера любопытным образом компенсируется другим изъяном в выведении закона. Так как время, за которое планета проходит по очень малой дуге, пропорционально радиус-вектору, сумма отрезков времени, за которое планета проходит сумму малых дуг, образующих конечную дугу орбиты, будет пропорциональна сумме всех радиус-векторов, то есть (как он думает) площади сектора, описываемого радиус-вектором. Это второй недостаток, так как сумма бесконечного числа линий, находящихся бок о бок, не составляет площади, и это Кеплер должен был прекрасно понимать. Тем не менее теория всемирного тяготения доказала истинность знаменитого второго закона Кеплера, а именно что время, требующееся, чтобы описать дугу орбиты, пропорционально площади сектора, описываемого радиус-вектором. Однако способ, которым Кеплер вывел свой закон, был отнюдь не бесспорным. Он так и не узнал об ошибке в своем законе расстояний, но понимал, что сумма нескольких радиус-векторов неверно измеряет площадь сектора; но все-таки, обнаружив, что средние аномалии можно точно рассчитать по его второму закону, причем они будут согласоваться с наблюдениями, и не только для орбиты Земли, к которой он сначала применял его, но и для эллиптической орбиты Марса, он справедливо посчитал это твердо установленным фактом. Однако Марс по-прежнему причинял Кеплеру немало хлопот, поскольку, когда он из наблюдений вблизи перигелия и афелия вывел новые значения элементов, сравнение с наблюдаемыми местами в других частях орбиты вновь выявили вопиющие ошибки, которые в октантах достигали 8?.

Этот последний результат заронил в Кеплере подозрение, что форма орбиты не круговая, и показал необходимость продолжать исследования без каких-либо предвзятых допущений относительно формы орбиты. Однако ее можно было бы определить при известных расстояниях от Марса до Солнца в разных частях орбиты. Поэтому Кеплер вычислил три расстояния на основании гипотезы о круговой орбите и наблюдений. Результат оказался таков:

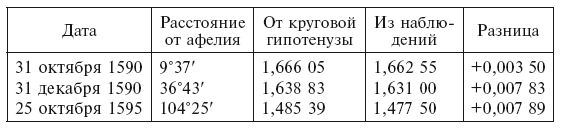
Поскольку наблюдаемые расстояния оказались меньше, чем рассчитанные из эксцентрического круга, следовал естественный вывод: орбита представляет собой не окружность, а кривую, которая, кроме как в апсидах, целиком лежит внутри круга. Это также объясняет, почему применение закона площадей дало результат, показывающий, что планета движется слишком быстро вблизи апсид и слишком медленно на среднем расстоянии, так как площади секторов круга везде, кроме как вблизи апсид, больше, чем у кривой, лежащей внутри круга. Поэтому Кеплер пришел к выводу, что «орбита планеты является не кругом, но овалом». В апсидах этот овал совпадает с кругом, а в аномалиях 90° и 270° больше всего отклоняется от круга, причем овал имеет яйцевидную форму, более широкую в афелии и более заостренную в перигелии. Чтобы объяснить эту примечательную форму орбиты, Кеплер разложил движение планеты на движение по эксцентрической окружности и движение по эпициклу. Он предположил, что планета обладает некой силой, противостоящей силе, исходящей от Солнца, которая толкает ее вперед, так что она описывает эпицикл попятным движением, а также он предположил, что планета движется неравномерно (в соответствии со вторым законом) на эксцентре, но равномерно на эпицикле.

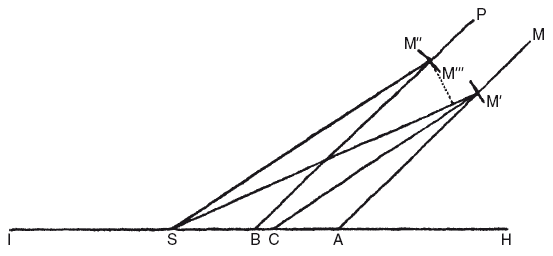
Таким образом, Кеплер окончательно распрощался с гипотезой о круговой орбите, но зато столкнулся с большими трудностями при работе с яйцевидной орбитой и ее квадратурой, так что ему пришлось прибегнуть к приближенным методам. Заместительная теория с достаточной для этой цели точностью давала гелиоцентрическую долготу, то есть направление радиус-вектора; осталось только определить длину. Поэтому линия от перигелия до афелия (IH) сначала была поделена на неравные части, так что АС = 0,072 32 и SC = 0,113 32, где S — Солнце. Затем угол ХАМ был сделан равным средней аномалии, а из С проведена линия SM?, равная по длине среднему расстоянию Марса. Тогда SM? будет истинным гелиоцентрическим направлением Марса.

Затем AS делится надвое в точке В, и ВР проведена параллельно AM, так что НВР – это средняя аномалия, тогда окружность вокруг B даст расстояние. На BP отмечен отрезок BМ?, равный среднему расстоянию, тогда SM? – истинная длина радиус-вектора, и если сделать SМ? = SМ?, то М? (расположенная на линии SМ?) будет истинным местом планеты.

Для нахождения площадей секторов овала Кеплер заменил овал эллипсом, причем наибольшая ширина лунки между ним и эксцентрической окружностью равна 0,008 58[343]. Это также дало ошибку примерно в 7? в октантах, но со знаками противоположными знакам эксцентрической окружности показав, что истинная орбита находится где-то между окружностью и вспомогательным эллипсом[344]. После ряда других бесплодных экспериментов он вычислил двадцать два расстояния от Марса до Солнца с помощью новой гипотезы. Эти вычисления демонстрируют, что он правильно определил линию апсид, и самым убедительным образом доказывают, что на самом деле она проходит через тело Солнца, как он всегда утверждал, а не через среднее Солнце. Но расстояния оказались слишком малы, с разницей 0,006 60 примерно в месте среднего расстояния. Поэтому истинная орбита со всей ясностью оказалась расположена между кругом и овалом.

Ширина лунки между орбитой Марса и эксцентрической окружностью наконец дала долгожданный ключ к тайне движения планеты. Она составляла 0,006 60, при полудиаметре окружности 1,523 50, или 0,004 32, если полудиаметр равен 1. Это почти равно 0,004 29, или половине ширины лунки в теории овала. По чистой случайности, как признает Кеплер, он заметил, что 1,004 29 равно секансу наибольшего оптического уравнения Марса, то есть секансу угла (5°18?), тангенс которого равен эксцентриситету. «Я как будто пробудился ото сна, и меня озарило новым светом». На средних расстояниях оптическое уравнение является максимальным, и там сокращение расстояний оказывается наибольшим, превышая единицу на 1,004 29. Этот результат Кеплер распространил на все точки орбиты, заменив всюду радиус-вектор эксцентрической окружности на одинаковую величину, умноженную на косинус оптического уравнения, или distantia diametralis, как он это называет. Сравнение ряда расстояний, вычисленных по этому правилу, с результатами, получившимися из наблюдений Браге, показало, что это предположение вполне оправданно. Так было сделано великое открытие, что радиус-вектор Марса всегда представлен уравнением

г = а + ае cos Е,

где а — среднее расстояние, а Е — эксцентрическая аномалия, отсчитанная по старому обыкновению от афелия, тогда как ае — расстояние между Солнцем и центром орбиты. Хотя фактически цель была достигнута, в последнюю минуту Кеплер все же нашел новые неприятности на свою голову. Уменьшение радиус-вектора по мере удаления планеты от афелия позволило предположить либрацию планеты по диаметру эпицикла, движущегося по окружности, концентрической с Солнцем. Но хотя это могло представить вышеприведенное уравнение, то есть длину радиус-вектора, попытка вычислить таким способом соответствующую истинную аномалию привела к ошибкам в 4? или 5?. Это заставило Кеплера вернуться к эллипсу, который он уже использовал в качестве замены овалу, и наконец он доказал, что эллипс с Солнцем в одном из фокусов дает длину радиус-вектора, согласующуюся с вышеописанным уравнением, тогда как его направление получается из

r cos ? = ае + а cos Е.

Большая проблема в конце концов была решена, проблема, которая сбила с толку гениального Евдокса и оказалась камнем преткновения для александрийских астрономов, так что Плиний даже назвал Марс «звездой, не поддающейся наблюдению». Многочисленные наблюдения Тихо Браге, сделанные с недостижимой дотоле точностью, в умелых руках Кеплера выявили неожиданный факт, что Марс описывает эллипс, в одном из фокусов которого находится Солнце, а радиус-вектор планеты охватывает равные площади в равные промежутки времени. Гений и поразительное терпение Кеплера доказали не только то, что эта новая теория удовлетворяет наблюдениям, но и то, что никакую другую гипотезу невозможно согласовать с наблюдениями, так как все предлагаемые альтернативы сохраняют вопиющие ошибки, которые никак невозможно было отнести на счет ошибок наблюдения. Таким образом, Кеплер, в отличие от всех своих предшественников, не просто выдвинул новую гипотезу, которая могла, как и другая, позволить математику-расчетчику составить таблицы движения планет; он нашел фактическую орбиту, по которой планета летит через пространство. В пятой и последней части своей книги о Марсе он наконец показал, как идеально новая теория отображает наблюдаемые широты. Долготы уже доставили немало хлопот предыдущим теоретикам, но широты были просто безнадежным случаем и доводили астрономов до самых необоснованных предположений, например об орбитальных колебаниях. Теперь, когда был установлен истинный характер орбиты и доказано, что ее плоскость пересекается с плоскостью орбиты Земли на линии, проходящей через Солнце, все стало ясно, и многие до той поры необъяснимые явления сразу оказались объяснены. Среди них был и тот факт, что широта не всегда максимальна точно в момент противостояния, и Кеплер цитирует и рукописи Браге, и свои беседы с ним, чтобы показать, какое беспокойство это вызывало у великого астронома-практика. Теперь проблема превратилась в вопрос: меняется ли быстрее всего синус гелиоцентрической широты или расстояние между Марсом и Землей, и так астрономы-теоретики освободились еще от одного источника затруднений.

Открытие эллиптической орбиты Марса стало абсолютно новой отправной точкой, так как наука отказалась от принципа равномерного кругового движения, принципа, который издавна считался самоочевидным и неприкосновенным, хотя еще Птолемей молчаливо опустил его, введя эквант. Поэтому пытливый ум Кеплера не мог не попытаться объяснить, почему планета описывает эллиптическую, а не круговую орбиту.

В «Тайне мироздания» Кеплер предположил существование anima motrix у Солнца и теперь начал дальше развивать эту идею. Эта сила исходит от Солнца, но, в отличие от света, распространяется не во все стороны, а только в плоскости, близко к которой расположены плоскости всех планетных орбит, так что она просто уменьшается по мере увеличения расстояния. Скорость движения планеты по орбите, следовательно, изменяется обратно пропорционально расстоянию, и эта идея, как мы уже видели, привела Кеплера к открытию его второго закона. Но правило нельзя было просто распространить с одной орбиты на другую, ведь тогда периоды обращения были бы пропорциональны квадратам расстояний. Солнечная сила производит обращение планет, потому что Солнце вращается вокруг своей оси и таким образом вместе с собой вращает прямые линии, по которым распространяется сила, с запада на восток. В результате образуется круговой поток или вихрь, который уносит планеты за собой, но их периоды обращения отличаются по причине разного сопротивления, оказываемого каждой планетой, которое зависит от ее массы. Естественно было предположить, что солнечный экватор совпадает с эклиптикой, а период вращения Солнца был определен весьма любопытным образом. Периоды обращения планет, находящихся ближе к Солнцу, короче, чем у планет, находящихся дальше, так что период вращения Солнца должен быть меньше 88 дней – периода обращения Меркурия. Кеплер предполагает, что полудиаметры Солнца и орбиты Меркурия находятся в том же соотношении друг к другу, как полудиаметры Земли и орбиты Луны, следовательно, периоды должны находиться в том же отношении, и так мы получаем период вращения Солнце равный примерно трем дням. Несколько лет спустя, когда вскоре после изобретения телескопа были открыты солнечные пятна, Кеплер вынужден был признать[345], что эта оценка и предположение о положении солнечного экватора оказались одинаково ошибочными.

Вихри, вызываемые Солнцем, увлекают планеты по круговым орбитам, концентрическим с Солнцем, и поэтому необходимо найти какую-то силу, способную превратить это круговое движение в эллиптическое. Еще до публикации книги Гильберта «О магните» Кеплер много интересовался магнетизмом, как нам известно из писем, написанных в 1599 году баварскому канцлеру Герварту фон Хоненбургу; и он неоднократно пытался найти положение магнитных полюсов Земли с помощью тех немногих определений магнитного склонения, которые были ему доступны. Сначала он считал, что северный полюс на 23°28? отклоняется от магнитного полюса и что магнитный полюс указывает на место, где находился полюс вращения в момент сотворения, так как, когда два полюса постепенно разошлись, экватор Земли приобрел наклон относительно эклиптики. После этого на основании наблюдений, сделанных голландской экспедицией на Новую Землю, он пришел к выводу, что два полюса отстоят лишь на 6?° друг от друга, что, как ему казалось, хорошо вписывается в теорию Доменико Марии Новары, что положение земной оси изменилось на 1°10? со времен Птолемея и за 5600 лет, прошедших с момента сотворения мира, разница составит более 5°. Хотя Кеплер после публикации книги Гильберта и после того, как он получил доступ к большему числу измерений склонения, и признал, что невозможно определить положение магнитного полюса подобными способами, он продолжал глубоко интересоваться магнетизмом, считая, что это явление способно объяснить эллиптическое движение планет.

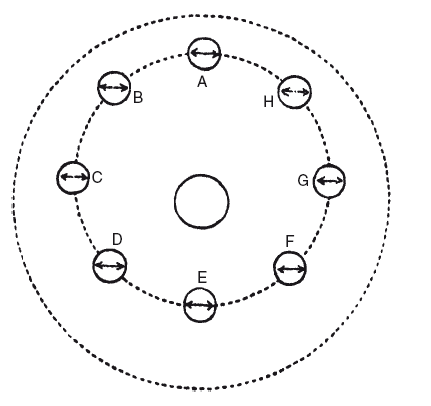
По Кеплеру, каждая планета имеет магнитную ось, которая всегда указывает в одну и ту же сторону и остается параллельной самой себе, так же как ось вращения Земли, не требуя «третьего движения», постулированного Коперником. Он оправдывает то утверждение, что планеты – это «огромные круглые магниты», ссылаясь на тот факт, что, как доказал Гильберт, так дело обстоит с Землей, которая, по Копернику, является одной из планет.

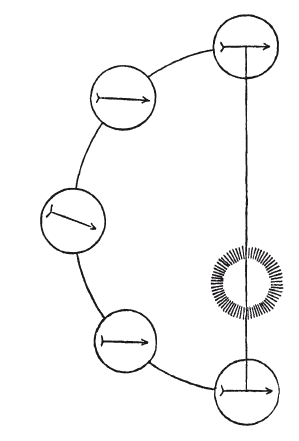
Один из магнитных полюсов планеты стремится к Солнцу, а второй отталкивается им. Для начала рассмотрим положение планеты в точке А, где магнитные полюса находятся на одинаковом расстоянии от Солнца; Солнце не притягивает и не отталкивает планету, а просто движет ее. Но при этом движении планета последовательно проходит через положения В, С, D, Е, и полюс, «дружественный к Солнцу» (soli arnica), поворачивается к Солнцу, в то время как «враждебный» (discors) отворачивается от него. Поэтому в данной части орбиты планета притягивается Солнцем и продолжает приближаться к нему до положения Е, где притяжение и отталкивание снова уравновешивают друг друга. Когда планета проходит Е, враждебный полюс поворачивается к Солнцу, и поэтому планета во второй половине орбиты отталкивается Солнцем, и расстояние возрастает вплоть до достижения афелия в А. Однако ось не остается строго параллельной первоначальному направлению, но вследствие действия Солнца претерпевает небольшое отклонение, так что она указывает точно на Солнце, когда планета находится на среднем расстоянии. В верхнем квадранте, от афелия до среднего расстояния, Солнце производит этот «наклон» в течение более длительного времени, но сила его слабее, в нижнем квадранте – в течение более короткого времени, но с большей силой, fltque compensatio perfecta. Если магнитная ось после полного оборота не совсем возвращается в исходное положение, в результате происходит медленное движение линии апсид, которое наблюдается в действительности. Величина эксцентриситета отличается у разных планетных орбит в силу отличающейся интенсивности магнетизма у каждой планеты, но конечная причина состоит в том, что отношение наибольшей к наименьшей скорости должно быть гармоничным.

Планеты движутся в плоскости солнечного экватора, то есть эклиптики (не имея широты), за исключением наклона оси каждой планеты к эфирному течению, производимому Солнцем, которое отклоняет планету, как руль – корабль.

Данное Кеплером объяснение движения планет – это первая серьезная попытка истолковать механизм Солнечной системы. Он не пошел дальше понятий механики, бытовавших в XVI веке, так как он предполагает, что для продолжения движения планеты требуется постоянное воздействие некой силы и что планета остановится на месте, как только сила перестанет действовать. Активная сила магнетизма ясна и проста, и Кеплер не уставал подчеркивать это при всякой возможности. Так, тезис № 51 его маленькой полемической брошюры Tertius Interveniens (1610) утверждает, что «планеты являются магнитами и приводятся в движение вокруг Солнца магнитной силой, но живо только одно Солнце»[346].

Хотя Кеплер и достоин всяческого уважения за попытку найти причину движения по орбите, его нельзя может назвать предтечей Ньютона. В его гипотезе сила направлена не к Солнцу, а по касательной, это «не притяжение, а продвижение», как он выразился в письме Местлину в марте 1605 года. Если бы Солнце не вращалось, не обращались бы и планеты, как если бы не вращалась Земля, не обращалась бы и Луна вокруг нее; но Луна не имеет вращения, поскольку у нее нет спутника, «поэтому в случае Луны вращение было опущено по причине ненужности». Но Юпитер и Сатурн должны вращаться вокруг своей оси, поскольку у них есть спутники[347]. Вращение планеты частично вызывается силой Солнца, но в основном силой, присущей самой планете; так, Земля вращается 365 раз за один оборот вокруг Солнца, из которых Солнце производит пять, тогда как Земля без его влияния вращалась бы лишь 360 раз.

Таким образом, мы видим, что гравитация не имела места в теории небесной механики Кеплера. И тем не менее его идеи о тяготении в значительной мере превосходят представления, господствовавшие еще со времен Аристотеля. Как обычно, мы находим зачатки его идей в «Тайне мироздания»: «Никакая точка, никакой центр не имеет тяжести, но все, имеющее ту же телесную природу, будет стремиться к нему; центр также не приобретает вес, притягивая к себе другие вещи или будучи объектом их стремления, как и магнит не становится тяжелее, когда притягивает к себе железо». В предисловии к книге о Марсе «истинное учение о тяготении» излагается в следующих аксиомах. Любое физическое вещество покоится в том месте, в котором оно помещено изолированно от действия силы другого тела того же рода (extra orbem virtutis cognati corporis). Тяготение является взаимной тенденцией родственных тел к соединению друг с другом (к тому же роду относится магнитная сила), так что Земля притягивает камень гораздо сильнее, чем камень притягивает Землю. Если предположить, что Земля находится в центре мира, то тяжелые тела не стремятся к центру мира как таковому, но к центру круглого родственного тела – Земли; и куда бы ни перемешалась Земля, тяжелые тела всегда будут к ней стремиться; но если бы Земля не была круглой, они бы не стремились со всех сторон к середине, но с разных сторон увлекались бы к разным точкам. Если бы два камня находились в любом месте пространства друг рядом с другом, но вне досягаемости третьего родственного тела, они бы, подобно двум магнитным телам, соединились в промежуточной точке, причем каждый приблизился бы к другому пропорционально притягивающей массе. И если бы Земля и Луна не удерживались на своих орбитах их одушевляющей силой (vi animali), то Земля поднялась бы к Луне на ¹/₅₄ долю расстояния, в то время как Луна опустилась бы на остальную часть пути и соединилась бы с Землей, при условии что оба тела имеют одинаковую плотность. Если бы Земля перестала притягивать воду, все моря поднялись бы и перетекли на Луну. С другой стороны, virtus tractoria Луны достигает Земли и производит приливы, о которых и их влиянии на формирование заливов и островов Кеплер много рассуждает, но эти рассуждения мы здесь опустим.

Поразительно, как точно удалось Кеплеру ухватить близкое сходство между гравитацией и магнетизмом – с одной стороны, и между движущей силой Солнца и магнетизмом, с другой. И все же он не смог увидеть тождественности силы тяготения и силы, удерживающей планеты на орбитах. Это тем более примечательно, что в примечаниях к своему Somnium, «Сну», написанному между 1620 и 1630 годами, Кеплер открыто приписывает приливы тому, что «тела Солнца и Луны притягивают воды моря с определенной силой, подобной магнитной». Он признавал, что притяжение Солнца (а не только исходящей от него тангенциальной силы) может достигать Земли. Но на этом он остановился и не мог пойти дальше, не пересмотрев всю свою концепцию причин движения тел.

Кеплер был очень плодовитым автором, и не только книг, но и писем, и, так как он писал очень открыто о своей работе и так как его переписка, к счастью, сохранилась, мы можем проследить ход его исследований из года в год. Так, в июле 1600 года он писал Герварту, что два предположения, сделанные в «Тайне мироздания», уже подтвердились: использование истинного места Солнца вместо среднего и существование экванта в солнечной орбите. 1 июня 1601 года он описал Маджини, как использовал четыре противостояния, и объяснил, что неравенства низших планет возникают из движения Земли, что наклоны постоянны и что теории всех семи планет должны быть схожими. В первой половине 1602 года он обнаружил, что орбита Марса имеет овальную форму; но 1603 год он почти полностью посвятил своей книге по оптике и к работе с Марсом вернулся не раньше начала 1604 года, как мы узнаем из письма Лонгомонтану от следующего года, где Кеплер добавляет, что он пока еще ясно не увидел причину овальной формы орбиты кроме того, что это было связано с исходящей от Солнца силой; к тому времени у него была написана пятьдесят одна глава. Главы LIII—LVIII были написаны около мая 1605 года, а до конца года – глава LX, которой он завершил теорию движения по долготе, а остальные десять глав о широте, видимо, были написаны не раньше 1606 года. В декабре 1606 года император пожаловал 400 флоринов на печать, и они были действительно выплачены, что в то время нечасто случалось с императорскими пожалованиями. Рукопись была отправлена в печать в сентябре 1607 года, и книга увидела свет в июле или августе 1609 года[348] под названием Astronomia nova aixioXoyr|TO(; seu Physica Coelestis, tradita commentariis de motibus stellae Martis. Ex observationibus G.Y. Tychonis Brahe («Новая астрономия, причинно обоснованная, или небесная физика, основанная на комментариях к движениям звезды Марс, наблюдавшихся достопочтенным Тихо Браге»). В истории астрономии есть еще только два других столь же важных труда: это «О вращении небесных сфер» Коперника и «Начала» Ньютона. «Астрономия без гипотез», которую требовал Раме, наконец-то появилась, и Кеплер с полным правом мог заявить (на обратной стороне титульного листа), что, если бы Раме был еще жив, он мог бы претендовать на награду за это достижение – профессорскую должность, которую занимал Раме.

Среди корреспондентов Кеплера одним из самых достойных для обмена мыслями был Давид Фабрициус, протестантский пастор в Рестерхаве, с 1603 года в Остеле, что в Восточной Фрисландии, очень способный наблюдатель, который в 1598 году провел некоторое время с Тихо Браге в гольштейнском Вандсбеке и вновь посетил его в Праге в июне 1601 года и пробыл там несколько недель в отсутствие Кеплера[349]. Их переписка продолжалась с 1602 по 1609 год, и Кеплер держал

Фабрициуса в курсе хода его работы над Марсом[350]. Фабрициус был приверженцем системы Тихо Браге и так и не сумел осознать, что по существу она не отличается от системы Коперника, и поэтому всегда пытался определить абсолютное движение Марса относительно Земли, вместо того чтобы спокойно исследовать его гелиоцентрическое движение. В 1602 году Кеплер рассказал ему о заместительной гипотезе, а в июле 1603 года перевел специально для Фабрициуса свой метод определения расстояний в систему Тихо Браге и сообщил о важном открытии, что орбита Марса представляет собой овал. Он даже рассказал ему о приближенном методе, который применил для нахождения направления и длины радиус-вектора, и неудаче с истинными аномалиями (desperata res erat). Затем последовали несколько писем, в которых Фабрициус приводил различные возражения против полученных Кеплером результатов относительно Солнца и Марса, на которые Кеплер пространно ответил в феврале 1604 года. Потом наступила пауза, пока Фабрициус в письме от 27 октября 1604 года не объявил, что, сравнив данные со своими собственными наблюдениями, он нашел, что овальная гипотеза дает слишком малый радиус-вектор Марса для среднего расстояния. Кеплер упоминает об этом в главе LV своей книги и великодушно прибавляет, что Фабрициус, таким образом, почти опередил его в нахождении истинной теории[351]. Однако на самом деле это большое преувеличение, ибо, даже если бы Кеплер забросил свое исследование, Фабрициус никогда бы не обнаружил эллиптическую форму орбиты, которую он, более того, называл абсурдной и упорно не желал принимать, когда Кеплер ее таки открыл. И каких бы похвал ни заслуживал Фабрициус за то, что увидел недостатки овальной гипотезы, Кеплер обнаружил все то же самое еще до получения его письма и смог уже 18 декабря 1604 года сказать Фабрициусу, что орбита Марса является идеальным эллипсом[352].

Консервативному мышлению Фабрициуса оказалось не под силу отказаться от древнего принципа сочетаний круговых движений, и поэтому он разработал свою собственную теорию, только чтобы не признавать эллиптического движения. Если на окружности круга движется эпицикл, в то время как планета движется на эпицикле в противоположном направлении с удвоенной скоростью, планета будет описывать эллипс. Фабрициус предпочел трансформировать эту конструкцию, позволив центру эксцентра совершать колебания (либрации) в своей плоскости по прямой линии, перпендикулярной к линии апсид. Таким образом он представил эллиптическое движение, но не движение по второму закону Кеплера, при этом истинная аномалия не соответствовала правильной средней аномалии. Фабрициус изложил свою теорию в письме от февраля 1608 года и записи от 2 октября 1608, но так ничего и не публиковал по этому вопросу, и Кеплер уделяет его теории лишь несколько строк в своем Epitome astronomiae copernicanae, «Кратком изложении коперниканской астрономии». Но все же Давид Фабрициус заслуживает достойного места среди теоретиков астрономии XVII века, хотя он и был одним из последних приверженцев принципа, которому вскоре суждено будет окончательно впасть в забвение.

Кеплер собирался написать систематический трактат по астрономии, подобный «Синтаксису» Птолемея, сделав для других планет то же, что сделал для Марса. Книга должна была называться «Гиппарх» в честь великого астронома. Но хотя Кеплеру удалось добиться значительного прогресса в части, касающейся движения Луны, разные обстоятельства заставили его изменить свой план, и вместо «Гиппарха» он написал более элементарный учебник Epitome astronomiae copernicanae в трех частях, первая из которых была опубликована в 1618 году в Линце, куда Кеплер переехал в 1612 году в качестве «провинциального математика»; две остальные части последовали в 1620 и 1621 годах. Этот труд предполагал, что два первых закона Кеплера, которые сначала были доказаны только для Марса, распространяются и на другие планеты. Что касается Луны, то Кеплер нашел введение эллиптического движения в теорию очень хлопотным делом вследствие изменчивости эксцентриситета, и в течение ряда лет он вносил множество изменений в свое представление наблюдаемых долгот. Должно быть, он часто завидовал предшественникам, которые могли ввести эпицикл, чтобы объяснить каждое новое неравенство. Независимо от Браге Кеплер нашел годовое уравнение Луны. Солнечное затмение 7 марта (по новому стилю) 1598 года, а также лунное затмение в феврале и пасхальное полнолуние произошли на час с лишним позже, чем гласил составленный им календарь, а лунное затмение в августе того же года случилось раньше, чем ожидалось. Поэтому в календаре на 1599 год Кеплер предположил, что период обращения Луны относительно Солнца зимой немного длиннее, чем летом. В январе 1599 года Герварт фон Хоненбург предложил ему более полно объяснить этот вопрос, и Кеплер в своем ответе высказал гипотезу, что Луна может задерживаться в своем движении под действием исходящей от Солнца силы, которая зимой, когда Земля и Луна находятся ближе к Солнцу, больше, чем летом. Причиной этого явления может быть также то, что скорость вращения Земли зависит от расстояния от Земли до Солнца, то есть она немного быстрее зимой, так что в это время года Луне, по-видимому, требуется больше времени, чем летом, чтобы описать точно такую же дугу. Эта мысль далее развивается в Epitome. Кеплер применил такую же поправку, как и Браге, с использованием другого уравнения времени для Луны, но величину годового уравнения, которая у Браге составила 4,5?, Кеплер нашел верно: II?[353].

Новые планетные таблицы – «Рудольфинские», над которыми Кеплер работал на протяжении многих лет, были опубликованы в 1627 году в Ульме под личным надзором Кеплера, который для этого оставил Линц и перебрался в Ульм в конце предыдущего года. Весьма характерный для благородства автора жест: прямо на титульном листе он заявил, что таблицы содержат возрожденную астрономию, задуманную и осуществленную Тихо Браге, «фениксом астрономов».

Но задолго до завершения этой работы гений Кеплера одержал еще один триумф: открытие третьего закона движения планет. Он содержится в его труде Harinonices Mundi Libri Y, «Гармонии мира», опубликованном в Линце в 1619 году в продолжение «Тайн мироздания», завершая, к удовлетворению автора, цепочку идей о гармонии мира, занимавших его ум с юности.

Надо помнить, что главным желанием Кеплера, когда он приехал к Тихо Браге в Чехию, было получить способ вычисления более точных значений средних расстояний и эксцентриситетов планет, чтобы проверить его теорию пяти правильных многогранников. Когда после многих лет кропотливого труда он вычислил расстояния на основе наблюдений Браге, оказалось, что теория лишь приблизительно верна, поскольку соседние планетные сферы неточно совпадают со сферами, вписанными в соответствующие многогранники или описанными вокруг них. Из этого Кеплер сделал вывод, что расстояния планет от Солнца берутся не просто из правильных геометрических тел, каковая идея, казалось бы, подтверждается тем обстоятельством, что максимальные и минимальные расстояния двух планет дают четыре соотношения, то есть во всей планетной системе содержатся двадцать отношений расстояний последовательно расположенных планет, в то время как геометрические тела дают только пять. Отклонение устройства мира от пяти правильных тел, а также меняющиеся расстояния между планетами в процессе их обращения являются следствием «гармонии мира», и эту гармонию следует искать в наибольших и наименьших расстояниях планет от Солнца, поскольку требуется найти закон, определяющий форму орбиты, то есть эксцентриситет. Сами расстояния не производили такого впечатления, будто между ними существует какая-либо гармония, из чего следовало, что его нужно искать в движениях планет (in ipsis motibus, non in intervallis), то есть в угловых скоростях с точки зрения общего источника движения – Солнца. В нижеследующей таблице для каждой планеты приведена гелиоцентрическая угловая скорость (суточное движение) в афелии и перигелии.

Здесь мы можем сразу же отметить, что гармония для Кеплера – это всего лишь математическая концепция; он не воображает, будто в самом деле существует какая-то «музыка сфер»: «lam soni in coelo nulli existunt, пес tarn turbulentus est motus, ut ex attritu aurae coelestis eliciatur stridor». Суточная гелиоцентрическая угловая скорость в секундах представляет число колебаний определенного тона, но по мере изменения скорости в процессе обращения тон не остается одним и тем же, но проходит через музыкальный интервал, длина которого зависит от эксцентриситета и может быть легко определена, если за наименьшую скорость считать число колебаний, которые основной тон совершает в единицу времени. Но положение интервала должно каким-то образом зависеть от абсолютной длины радиус-вектора, поэтому нужно найти закон, связывающий среднее движение (или период обращения) со средним расстоянием, так как если бы гармония небес существовала, то из нее можно было бы вычислить среднее расстояние. Это вычисленное расстояние затем нужно согласовать с наблюдаемым. После многочисленных попыток 15 мая 1618 года Кеплер открыл свой знаменитый третий закон, гласящий, что квадраты периодов обращения любых двух планет пропорциональны кубам их средних расстояний от Солнца. Этому закону он вскоре нашел применение не только для планет, но и для четырех недавно обнаруженных спутников Юпитера.

Итак, есть три способа, которыми созвучие может проявляться в движении планет. Во-первых, отношение самого медленного движения в афелии к самому быстрому движению в перигелии является интервалом по причине эксцентриситета планетной орбиты. Из приведенной выше таблицы видно, что интервалы почти идеально созвучны, так как диссонанс меньше полутона, за исключением случаев Земли и Венеры вследствие их малых эксцентриситетов. Во-вторых, крайние точки движения двух соседних планет можно сравнить двояко друг с другом, поскольку интервал можно либо взять от самого низкого тона (движение в афелии) внешней планеты до самого высокого тона (перигелий) следующей ниже планеты или от самого высокого тона внешней до самого низкого внутренней. Первый Кеплер называет расходящимся, а второй – сходящимся интервалом, и приведенная выше таблица показывает почти идеальное созвучие в обоих случаях, за исключением интервала между орбитами Марса и Юпитера, который согласуется с тетраэдром, а не с музыкальной теорией. В-третьих, созвучие может существовать между всеми шестью планетами.

Чтобы найти, к какой октаве относятся самый низкий и самый высокий тон каждой планеты, цифры, выражающие их наибольшую и наименьшую угловую скорость, следует разделить на некую степень числа 2 для получения соотношений меньше, чем 1:2, то есть в пределах октавы. Использованный показатель 2 тогда будет указывать на то, в какую октаву входит тон.

Принимая, что скорость Сатурна в афелии равна 0, самый низкий тон Земли также будет соответствовать ноте соль, так как эти два тона представлены значениями 1?46? и 1?47?, практически идентичными, но это будет высокая соль, на пять октав выше. Значение для самого высокого тона Меркурия 3?0? очень близко к ⁵/₃ от 1?47?, тон – ми E^?, на семь октав и большую сексту выше самого низкого тона Сатурна. Таким образом, планеты исполняют следующие мелодии:

Это очень интересное представление эксцентриситетов планет, ведь с первого взгляда видна большая разница между почти круговой орбитой Венеры и весьма значительным эксцентриситетом Меркурия. Разрыв, как известно разделяющий орбиты Марса и Юпитера, тоже сразу бросается в глаза.

Мы бы рисковали зайти слишком далеко, если бы попытались здесь показать, как Кеплер подбирал интервалы между шестью планетами, чтобы заставить производимый ими хор звучать в абсолютно идеальной гармонии. В конце концов он получает следующие соотношения наименьшей и наибольшей скорости:

Сатурн 64 : 81

Юпитер 6561 : 8000

Марс 25 : 36

Земля 2916 : 3125

Венера 243 : 250

Меркурий 5 : 12

С этими новыми значениями он вычисляет новые эксцентриситеты, средние движения и – по своему третьему закону – средние расстояния. Совпадение этих значений расстояний с наблюдаемыми выглядит следующим образом, причем среднее расстояние от Земли до Солнца предполагается равным 1000.

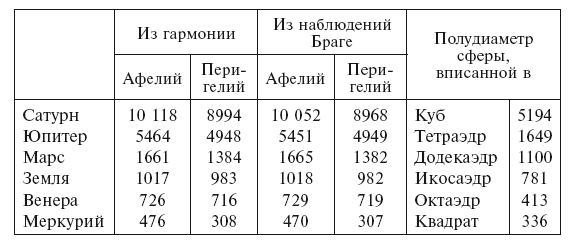
Последний столбец таблицы показывает, насколько теория пяти правильных тел согласуется с гармонией. Грани куба спускаются чуть ниже среднего расстояния Юпитера, в то время как грани октаэдра не совсем достигают среднего расстояния Меркурия; грани тетраэдра пересекают внешнюю сферу Марса, но грани додекаэдра и икосаэдра не доходят до внешних сфер Земли и Венеры. Как предполагается, это показывает, что отношения орбит, выведенные из теории правильных тел, не непосредственно, но лишь косвенно выражены в реальных планетных орбитах через гармонию.

Многие авторы выражали глубокое сожаление по поводу того, что Кеплер потратил столько времени на сумасбродные домыслы и заполнил свои книги всяческими мистическими фантазиями. Но это основано на неправильном понимании цели Кеплера в его исследовании тайн мироздания и мировой гармонии, ведь даже в своих самых смелых рассуждениях он брал за основу факты, полученные с помощью тщательных наблюдений, и ставил себе целью и получал результаты большого практического значения. Его стремлению разгадать «тайну» Солнечной системы мы обязаны гениальным открытием, что плоскости всех планетных орбит проходят через центр Солнца. Этот закон следовало бы назвать его первым законом, и неспособность Коперника его обнаружить сыграла большую роль в том, что его труд так и остался неполным. Упорство, с которым Кеплер цеплялся за свое место под руководством Тихо, о котором он сказал (и, возможно, довольно справедливо), что это был человек, неспособный жить, не подвергая себя величайшим оскорблениям[354], объясняется твердой решимостью построить свою систему многогранников на прочном фундаменте надежных и систематически сделанных наблюдений. Продолжению его работы в том же направлении мы обязаны первым и вторым законом Кеплера, а работе с гармонией – третьим. Таким образом, мы видим самую тесную связь между его домыслами и великими достижениями; без первых у нас никогда не было бы вторых.

Нам еще осталось сказать несколько слов о взглядах Кеплера на другие небесные светила. Хотя он во многом сумел освободиться от понятий древних, он все же разделял их мнение, что неподвижные звезды образуют часть твердой сферы, в центре которой находится Солнце. Мысль Джордано Бруно, что звезды – это солнца, окруженные планетами, Кеплер считает неправдоподобной, так как наше Солнце, если отдалить его на то же расстояние, будет светить гораздо ярче неподвижных звезд, хотя будет казаться таким же маленьким, как и они. Одно время он полагал, что и планеты, и звезды светятся собственным светом[355], но, узнав из Sidereus Nuncius, «Звездного вестника», Галилея о том, что в телескопе они выглядят совершенно разными, он признал, что неподвижные звезды излучают собственный свет, тогда как планеты непрозрачны и темны, «то есть, если воспользоваться словами Бруно, первые – это солнца, а вторые – луны или земли» [356]. Но в Epitome он не упоминает солнц. Там звездная сфера описывается как имеющая в толщину всего две немецкие мили, так что звезды находятся примерно на одном и том же расстоянии от Солнца. Это расстояние, по его прикидкам, равно 60 000 000 полудиаметров Земли, при условии что расстояние до Сатурна является средним геометрическим между расстоянием до звезд и полудиаметром Солнца, а также при условии, что полудиаметр Солнца равен 15 полудиаметрам Земли, а его параллакс не больше 1° – большой шаг вперед. Млечный Путь концентричен с Солнцем, так как делит небо на два полушария и почти везде предстает одинаковой ширины, так что Земля должна находиться примерно в его центре. Следовательно, Млечный Путь находится на внутренней поверхности звездной сферы.

Внутренняя поверхность сферы наполнена эфирным воздухом (aura aetherea), в котором движутся планеты. Время от времени этот воздух, или эфир, сгущается и становится непрозрачным для света Солнца и звезд, и это эфирное облако, которое мы зовем кометой, получает импульс от лучей Солнца и приводится в движение по прямолинейному пути через пространство, плывя по эфиру, словно кит или морское чудище по океану. Но образующее комету вещество постепенно разрушается под действием солнечного света и отталкивается в направлении солнечных лучей, образуя хвост, и таким образом комета вскоре растворяется. Хотя комета в течение своего существования движется по прямой (с постепенно увеличивающейся скоростью), ее путь кажется нам криволинейным по причине движения Земли. Неясно, почему он предполагает, что кометы не подвержены вихревому движению планет, с которым гораздо лучше согласовалось бы вращение вокруг Солнца, которое Браге приписывал кометам. Однако Кеплер полностью соглашался с Браге в признании того факта, что кометы являются не атмосферными явлениями, как учил Аристотель, а небесными, а также в отказе от аристотелевской доктрины неизменчивости всего, что находится в высшей области мира. Отсутствие параллакса у комет и появление новой звезды в 1572 году предоставило Браге много доводов против этого учения, а Кеплер обратил внимание на другие феномены, которые также указывали на изменения небесного вещества, как, например, необычный туман или дымка 1547 года и ореол света, видимый вокруг Солнца (корона) во время полного затмения 12 октября 1605 года. Новая звезда в созвездии Змееносца в 1604 году дала ему еще одно доказательство небесных изменений; он предположил, что она состоит из вещества, истекшего из звездной сферы, которое, когда звезда гаснет, снова возвращается в сферу[357].

Публикация «Рудольфинских таблиц» в 1627 году стала завершающим актом плодотворной жизни Кеплера. Он умер 15 ноября 1630 года, сумев полностью освободить систему Коперника от пережитков александрийской астрономии, от которых ее автору не удалось избавиться самому. Солнечная система отныне открылась во всей своей простоте, и единственные ее члены впервые были связаны воедино законом, соединяющим расстояния с периодами обращения.