Книга: История астрономии. Великие открытия с древности до Средневековья

Глава 11 Астрономы Востока

Глава 11

Астрономы Востока

Завоевания Александра Великого познакомили греков с миром Востока, который прежде посещало очень мало европейцев, они же и распространили греческую культуру во всех странах, до которых смог дойти победоносный македонец. Индийские провинции его империи вскоре после его смерти получили независимость, и, хотя распространение буддизма в III веке до и. э. сдержало продвижение эллинизма в Северной Индии, подъем греческого царства Бактрии и ее постепенное расширение на юг и восток в течение долгого времени поддерживало связь между Индией и Западом. Можно сомневаться, действительно ли, как утверждалось, индийская драматургия и архитектура находились под значительным влиянием контактов с эллинизмом, но совершенно несомненно то, что индийская астрономия является детищем александрийской науки.

В прежние времена астрономия в Индии развивалась лишь в самой незначительной степени. Индийцы имели некоторые представления о периодах Солнца и Луны и планеты Брихаспати (Юпитер), которые использовались с целью измерения времени, причем перемещения Луны особым образом диктовали моменты, когда следовало совершать жертвоприношения; но в остальном ранняя индийская астрономия, по-видимому, в основном ограничивалась астрологией, и нет никаких данных в пользу того, что точные знания о движении планет сложились в Индии раньше III века н. э. С того времени астрономия, которая дотоле являлась лишь предметом поэтических излияний, возникает как наука и в течение последующей тысячи лет трактуется в ряде учебников – сиддхант, содержание которых, якобы исходящее из божественного источника, испытало сильное влияние греческих авторов или попросту было заимствовано у них[220]. Тогда же впервые появляются семидневная неделя (прежде неизвестная) и посвящение каждого дня божеству одной из семи планет. Названия планет тоже стали греческими, например Асфудит (Афродита), Дьюгатих или Джива (Зевс), Хели (Гелиос) и т. п., в то время как зодиакальные знаки вытеснили двенадцать прежних, совершенно иных звездных групп, связанных с движением Солнца, и об их происхождении явно свидетельствуют их же названия:

Крийя, Тавури, Джитума, Каркин, Лейя, Патхена, Джука, Каурпья, Таукшика, Акокера, Хридрога, Иттха,

что соответствует греческим названиям зодиакальных созвездий:

Криос, Таурос, Дидюмос, Каркинос, Леон, Партенос, Зюгон, Скорпиос, Токсотис, Айгокерос, Идрохоос, Ихтис.

Множество других греческих терминов, связанных с геометрией, астрономией и астрологией, также перешло в труды на санскрите, поэтому греческое происхождение индийской астрономии можно считать убедительно доказанным. Кроме того, его открыто признавали некоторые ранние индуистские авторы, например Варахамихира, который цитирует яванов, то есть народы Запада, как источник сделанных им научных утверждений. Название «Ромака-сиддханты» (которая появилась не позже 400 г. н. э.) также безошибочно говорит о его происхождении из провинций Римской империи.

Астрономы сиддхант учили, что Земля – шар, висящий без опоры в пространстве, и отвергали древнее мифологическое представление о том, что Земля покоится на спине некоего животного, которое, в свою очередь, стоит на спине другого животного и так далее до самого последнего, которое опирается неизвестно на что. Бхаскара Ачарья, комментируя около 1150 года н. э. абсурдность этого представления, также отвергает и идею непрерывного падения Земли, поскольку она должна падать быстрее, чем стрела, пущенная вверх, по причине своей тяжести, поэтому стрела никогда не могла бы снова упасть на Землю. Вокруг Земли движутся планеты с одной и той же линейной скоростью. Диаметр Земли составляет 1600 йоджан, расстояние до Луны – 51 570 йоджан (или 64,5 радиуса Земли, что почти равно наибольшему расстоянию у Птолемея – 64¹/₆), в то время как расстояния до других планет вытекают из предположения о равных скоростях[221]. Уравнение центра планет находится при помощи эпицикла, и в эту систему индийцы добавляют собственное изобретение, предполагая, что эпицикл имеет переменную длину окружности, наибольшую, когда планета находится в апогее или перигее, и наименьшую, когда она находится в 90° от них, когда уравнение достигает своего максимума. Это ухищрение в виде вытянутого эпицикла одни астрономы применяли ко всем планетам, другие (Брахмагупта и Бхаскара) – только к Марсу и Венере, а третьи его полностью отвергали. Зачем нужно было так осложнять расчеты, непонятно. Арьябхата из Кусумапури или Паталипутры, родившийся в 476 году н. э., допустил еще одно отклонение от александрийских доктрин, как это следует из «Брахмаспхута-сиддханта» Брахмагупты, где он приводит следующую цитату из Арьябхаты: «Сфера звезд пребывает в неподвижности, а Земля, обращаясь, производит ежедневный восход и заход звезд и планет». Брахмагупта отвергает эту идею, говоря: «Если Земля движется на минуту за прану, то откуда и куда она направляется? Если она вращается, почему не падают с нее высокие вещи?» Но его комментатор Чатурведа Притхудака Свами отвечает: «Мнение Арьябхаты тем не менее удовлетворительно, ведь планеты не могут иметь два движения одновременно, таким образом опровергается возражение о том, что высокие вещи должны упасть; ибо нижняя часть Земли также и верхняя; поскольку, где бы ни стоял наблюдающий на поверхности Земли, это место и является наивысшей точкой».

Весьма интересно узнать теорию, которую когда-то пропагандировал Гераклит Понтийский, пересаженную на индийскую почву, особенно если вспомнить, что Селевк Вавилонский принимал эту теорию. Из Вавилона она могла легко попасть в Индию, хотя, конечно, в равной степени возможно, что та же мысль возникла у Арьябхаты совершенно независимо от греческих предшественников. Видимо, он списывал вращение Земли на ветер или течение воздушной среды, протяженность которого, согласно приписанной им Земле орбите, соответствует высоте чуть более 180 километров (183) от поверхности Земли, или 15 йоджан, тогда как диаметр Земли у него равен 1050 йоджанам (по 12,2 километра каждая). Это соответствовало распространенному в Индии мнению, что планеты увлекают по их орбитам мощные ветры, летящие с одинаковой скоростью параллельно эклиптике (в то время как один большой вихрь уносит все звезды вокруг Земли за двадцать четыре часа), однако планеты отклоняются от своих путей из-за каких-то невидимых сил, имеющих руки и вожжи, которыми они сбивают планеты с равномерного хода. Например, сила в апогее постоянно притягивает планету к себе, попеременно то правой, то левой рукой (как Лахесис в «Государстве» Платона), в то время как божество в узле отклоняет планету от эклиптики сначала в одну сторону, а затем в другую. И наконец, божество в точке соединения заставляет планету двигаться с переменной скоростью и иногда останавливаться и даже поворачивать вспять. Это с полной серьезностью изложено в «Сурья-сиддханте», и даже Бхаскара приводит эту теорию в своих примечаниях, хотя и опускает ее в основном тексте. Точно так же Брахмагупта, излагая теорию затмений, подтверждает существование восьмой планеты – Раху, которая является непосредственной причиной затмений; он обвиняет Варахамихиру, Арьябхату и прочих в отказе от этого ортодоксального объяснения данного феномена.

Индийская астрономия, таким образом, являет собой любопытную мешанину из древних фантастических идей и трезвых геометрических методов расчета. Последние в силу своего иноземного происхождения не могли изгнать старых понятий из астрономии. Как заметил Коулбрук, отсутствие самых характерных частей системы Птолемея – экванта и подробностей теорий Луны и Меркурия, по всей видимости, указывает на то, что греческая планетарная теория появилась в Индии позже Гиппарха и раньше Птолемея; и, за исключением отклонения эпицикла от круговой формы, индийцы не внесли в теорию никаких изменений или усовершенствований. Прецессия равноденствий, по их мнению, состояла в либрации в пределах 27° (у Арьябхаты 24°) к востоку и западу от среднего положения, однако они подошли гораздо ближе к истине, чем Птолемей, в отношении годовой величины, так как предполагали, что пройденное расстояние за век составляет I?°.

Несмотря на полную изоляцию Индии от Европы в Средневековье, индийской астрономии все же было суждено оказать косвенное влияние на развитие мировой науки. Благодаря завоеванию Персии в VII веке арабы, как и греки на тысячу лет раньше, вступили в контакт с Индией, откуда врачи и астрологи попали ко двору халифов еще до воцарения Харуна ар-Рашида. Мы располагаем подробным рассказом о том, каким образом индийская астрономия появилась в Багдаде, рассказом, вышедшим из-под пера астронома Ибн аль-Адами (умер до 920 г.), который подтвержден в знаменитых мемуарах об Индии Аль-Бируни, написанных в 1031 году. В 156 году хиджры (773 г.) перед халифом Аль-Мансуром предстал человек, прибывший из Индии; он был мастером в исчислении звезд, известном как синдхинд (то есть сиддханта), и владел методами решения уравнений на основе кардаджат (то есть крамаджья, синусов), рассчитанных для каждой половины градуса, а также методами расчета затмений и других явлений. Аль-Мансур заказал перевести на арабский книгу, в которой все это содержалось, и составить на ее основе труд, который мог бы послужить для расчета движения планет. Все это должным образом исполнил Мухаммад бен Ибрахим аль-Фазари, чьи труды арабы называют «Большой Синдхинд», и впоследствии Абу Джафар Мухаммад ибн Муса аль-Хорезми составил его краткое изложение для Аль-Мамуна, который использовал его для подготовки своих таблиц, получивших затем большую известность в мусульманских странах. А когда Аль-Мамун стал халифом, он стал поддерживать эти благородные изыскания и созвал самых образованных мужей, чтобы исследовать «Альмагест» и сделать инструменты для новых наблюдений.

Случай, изложенный выше вкратце, ясно показывает нам, откуда пошло изучение астрономии и математики при халифах-Аббасидах. Но хотя первый толчок они получили из Индии, дальнейшее развитие арабской науки было полностью основано на греческой и александрийской мысли. Через придворных врачей процветающей медицинской школы, которую держали христиане-несториане из Хузистана, изучение греческой философии и науки впервые стало распространяться среди подданных халифата; и труды Аристотеля, Архимеда, Евклида, Аполлония, Птолемея и других математиков постепенно переводились на арабский язык. Новые переводы Птолемея время от времени появлялись в разных царствах, на которые вскоре распался обширный халифат[222], и таким образом глубокие познания в астрономии Птолемея стали обычными на землях от Инда до Эбро. Несколько факторов способствовали тому, что мусульмане обратили особое внимание на астрономию, например необходимость определять сторону, к которой должны поворачиваться правоверные во время молитвы, а также важность движения Луны для мусульманского календаря, и то уважение, которым по всему Востоку пользовалась предсказательная астрология. Халиф аль-Мамун, сын Харуна ар-Рашида (813—833), был первым великим покровителем науки, хотя халифы-Омейяды еще задолго до того построили обсерватории близ Дамаска и еще до правления Аль-Мамуна еврей Машаллах (который умер около 815 г.) приобрел себе славу в качестве звездочета и астролога. Однако дамасскую обсерваторию совершенно затмила багдадская, возведенная в 829 году, где непрерывно велись наблюдения и составлялись таблицы движения планет, а также была сделана важная попытка определить размер Земли. Среди астрономов Аль-Мамуна и его наследников одним из величайших был Ахмад бен Мухаммад аль-Фергани (впоследствии известный на Западе под именем Альфраганус), чьи «Элементы астрономии» были переведены на латинский в XII веке и внесли большой вклад в возрождение науки в Европе[223]. Сабит ибн Курра (826—901) был чрезвычайно плодовитым писателем и переводчиком, но в истории астрономии больше всего известен тем, что поддерживал ошибочную гипотезу о колебательном движении равноденствий. Его младший современник Мухаммад аль-Баттани (умер в 929 г.) был самым прославленным среди всех арабских астрономов и стал известен на Западе в XII веке (под именем Альбатегний) по переводу введения к его таблицам[224]. Уже в его время халифы начали терять авторитет и вскоре утратили всякую светскую власть. Однако сокращение их поддержки никак не повлияло на изучение астрономии, так как персидский род Бундов, которые в 946 году приобрели пост амира аль-умара (соответствующий франкскому майордому), взял на себя роль покровителей науки, которую столь долго и с честью осуществляли халифы-Абба-сиды. В 988 году Шараф аль-Даула построил новую обсерваторию в саду своего дворца, и среди работавших там астрономов был Абуль-Вафа Мухаммад аль-Бузджани (959—998), который написал «Альмагест», чтобы сделать содержание птолемеевского труда доступным и для менее образованных людей. В XIX веке эта книга вызвала продолжительную полемику, который мы далее рассмотрим несколько подробнее.

В XI и XII веках мы не находим видных астрономов в мусульманской Азии. Однако между тем западные исламские страны уже готовились к тому, чтобы тоже внести свой вклад в поддержание математических наук. В фатимидском Египте Али ибн Абу Саид Абдеррахман ибн Ахмед ибн Юнус, обычно называемый ибн Юнус (умер в 1009 г.), прославился и как астроном, и как поэт. Щедро оборудованная каирская обсерватория позволила ему проверить планетные теории, когда-то разработанные в соседней Александрии, и в знак признательности тогдашнему правителю Аль-Хакиму он назвал свою работу «Зидж аль-Хакими» – «Таблицы аль-Хакима». Чтобы найти следующего астронома, нам нужно отправиться дальше на запад, где мы встречаем его в лице Абу Исхака Ибрахима аз-Заркали (в Европе впоследствии названного Арзахель). Он был родом из Кордовы, жил около 1029—1087 годов и работал над планетными таблицами, получившими название Толедских. В следующем столетии мы находим двух знаменитых севильских астрономов: это Джабир ибн Афлах, известный на Западе под именем Гебер (умер в 1145 г., его часто путают с великим алхимиком Джабиром ибн Хайяном VIII века[225]), и Нур ад-Дин аль-Битруджи (Альпетрагий). Оба они выступали против планетных теорий Птолемея, хотя сами не произвели ничего лучшего. Расцвет испанской астрономии продолжался какое-то время, хотя власть арабов на полуострове быстро слабела, и в XIII веке Испании удалось произвести на свет выдающегося человека, которого, хотя он и был христианским королем, следует упомянуть в обзоре арабской астрономии, поскольку всем, что он знал о науке, он был обязан примеру и учению мусульман и евреев. Король Кастилии Альфонсо X, прозванный Эль-Сабио (Мудрый, 1252—1284), последовал примеру халифов и призвал астрономов к своему двору, где они участвовали в подготовке знаменитых Альфонсовых таблиц.

После Альфонсо в Испании прекратилось изучение астрономии, но не раньше того, как оно возродилось на Востоке. В 1258 году багдадский халифат, еще существующий, но уже лишь как тень былого, был сметен монгольским завоевателем ханом Хулагу, внуком Чингисхана; но уже в следующем году этот великий воитель прислушался к совету своего нового визиря Насир ад-Дина ат-Туси (родился в Тусе, Хорасан, в 1201 г., умер в 1274 г.) и основал большую, великолепную обсерваторию в Мераге, в Северо-Западной Персии. В этой обсерватории, оснащенной множеством инструментов, частично новой конструкции, Насир ад-Дин и его помощники усердно наблюдали за планетами и после двенадцати лет труда произвели «Ильханские таблицы». Среди астрономов Мераге, по-видимому, был Абуль-Фарадж ибн Харун по прозвищу Бар-Эбрей, то есть «сын еврея». Он родился в 1226 году, был христианином, а с 1264 года до смерти в 1286 году – мафрианом, то есть главой восточных якобитов. Он оставил известную летопись[226] и астрономические труды, написанные по-сирийски, а также другие сочинения. Обсерватория в Мераге просуществовала недолго, и азиатской астрономии пришлось прождать полтора века, прежде чем внук другого ужасного завоевателя не воздвиг новую обсерваторию. Улугбек, внук Тамерлана, свез ученых людей в Самарканд и около 1420 года построил там обсерваторию, где были подготовлены новые планетные таблицы и новый звездный каталог впервые со времени Птолемея. Улугбек умер в 1449 году, он был последним великим защитником астрономии на Востоке; но в то самое время, когда в странах востока звезда Урании клонилась к закату, Европа снова увидела ее восход.

В этом кратком обзоре арабских астрономов мы упоминали только о тех, на чьи труды будем ссылаться на следующих страницах, и опустили несколько имен, чьи прославленные владельцы посвятили себя другим областям астрономии. Хотя Европа находится в долгу у арабов за сохранение живого пламени науки в течение многих веков и за наблюдения, которые до сих пор отчасти не потеряли ценности, мы не можем отрицать, что они оставили астрономию в основном в том же виде, в каком и нашли. Арабы заново определили несколько важных констант, но не внесли никаких улучшений в планетные теории. Поэтому будет достаточно перечислить, что пытались усовершенствовать и каких взглядов придерживались арабские астрономы, без соблюдения строго хронологического порядка, хотя здесь нам придется иметь дело с периодом около шестисот лет и представителями очень разных народов, которые имели друг с другом мало общего, помимо религии и языка, на котором они писали.

Обратившись в первую очередь к вопросу о форме Земли, мы находим примечательный контраст между Европой и Азией. Во всем исламском мире совершенно отсутствует та враждебность по отношению к науке, которая отличала Европу первой половины Средневековья. Хотя из «Космографии» Закарии аль-Казвини мы узнаем, что некоторые арабы в прошлом считали, будто Земля имеет форму щита или барабана, у нас все же нет никаких сведений о каких-либо гонениях на арабов, утверждавших, что Земля является шаром, со всех сторон которого могут обитать люди. Было ли это следствием того, что воины халифов дошли в своих походах до центра Франции с одной стороны и до границ Китая с другой, в то время как их купцы путешествовали на юг до Мозамбика и на север до центра Азии, это другой вопрос; во всяком случае, сам факт, что Земля является шаром очень малого размера по сравнению с размерами Вселенной, принимался без возражений всеми арабскими учеными, и самая первая научная работа, предпринятая после возникновения арабской астрономии, состояла в определении размера Земли. Она проводилась по приказу халифа Аль-Мамуна на равнине у Пальмиры. Как рассказывает Ибн Юнус, длину градуса измеряли два наблюдателя между Вамией и Тадмором и еще два в другом населенном пункте, название которого умалчивается. Первое измерение дало величину градуса 57, второе – 56? арабской мили по 4000 черных локтей, и приблизительное среднее значение – 56? мили – было принято в качестве окончательного результата. Таким образом, окружность Земли равна 20 400 арабским милям, а диаметр – 6500 милям. Другой отчет – Ахмада ибн Абдуллаха, известного под именем Хаббаш Аль-Хасиб, астронома при Аль-Мамуне (которого цитирует Ибн Юнус), утверждает, что группа наблюдателей (их имена не сообщаются) продвигалась по равнине Синджар и нашла разницу меридиональных высот, измеренную в тот же день, равную 1°, в то время как расстояние, которое они прошли, составило 56? арабской мили[227]. Вероятно, это два разных измерения. Если «черный локоть» равен египетскому и вавилонскому локтю, равному 525 миллиметра, то арабская миля = 2100 метра, а 56? мили = 119 000 метров – довольно большое число.

Доктрина шарообразной Земли остается неоспоримой в ученом мусульманском мире, хотя любопытное заблуждение о том, что уровень моря в некоторых частях Земли выше, чем в других, видимо, нашло своих сторонников в среде арабских авторов, как и в Европе[228]. Поэтому мы можем сразу же перейти к движениям небесных тел. Аль-Баттани определил долготу апогея Солнца и нашел ее равной 82°17?[229], или на 16°47? больше, чем у Птолемея. Так как он считал, что нашел значение Птолемея, и так как он принял 54? (или 1° за 66 лет) в качестве годовой величины прецессии, в расчетах (учитывая, что со времен Птолемея прошло 760 лет) осталась огромная ошибка 79? – 54? = 25? в год. В действительности годовое движение солнечных апсид составляет 11??, но все же можно сказать, что открытием этого движения мы обязаны Аль-Баттани, хотя он и не объявляет его открытием; фактически он просто приводит свое собственное значение как улучшенное птолемеевское. Даже Ибн Юнус (который нашел 86°10?) не подозревает, что апогей неуклонно сдвигается, но говорит лишь о том, что необходимо внести поправку на прецессию (1° за 70 лет), а также отмечает, что долготу апогея очень трудно определить с точностью[230]. С другой стороны, Аз-Заркали нашел меньшее значение – 77°50?, а так как он нашел и меньшее значение эксцентриситета, он посчитал необходимым допустить, что центр эксцентрической орбиты Солнца описывает меньший круг, по примеру, заданному Птолемеем для Меркурия. Наклонение эклиптики, которое греки нашли равным 23°51?20?, астрономы Аль-Мамуна нашли равным 23°33? (в 830 г.), Аль-Баттани (в 879 г.) и Ибн Юнус – 23°35?[231]. Когда Аз-Заркали нашел 23°33?, он, а потом и Абуль Хассан из Марокко, пришел к выводу, что наклонение колеблется между 23°53? и 23°33?, и вера в «трепет» равноденствий придала достоверность этой идее.

Если теперь мы обратимся к Луне, то обнаружим, что арабы никак не улучшили находок Птолемея. Некоторые заметили, что наклон лунной орбиты составляет не совсем 5°, как указано у Гиппарха. Так, Абуль Хасан Али ибн Амаджиур в начале X века говорит, что часто измерял максимальную широту Луны и нашел, что она больше, чем у Гиппарха, но при этом значительно и неупорядоченно варьируется. Ибн Юнус, цитируя это, добавляет, что он сам нашел 5°3? или 5°8?, тогда как другие наблюдатели говорят, что нашли значения от 4°58? до 4°45?[232]. Так из-за недостатка упорства и точных инструментов они проглядели замечательное открытие вариаций наклонения Луны.

Однако некоторые утверждают, что арабскому астроному принадлежит и еще более замечательное открытие. В 1836 году младший Седийо объявил, что нашел третье неравенство, вариацию, четко заявленную в «Альмагесте» Абуль-Вафы. В течение нескольких лет бушевали ожесточенные споры касательно достоверности этого открытия, причем Седийо в одиночку отчаянно защищал своего героя и отказывался выслушивать какие-либо доводы, тогда как Био, Либри и другие с такой же настойчивостью утверждали, что Абуль-Вафа всего лишь говорил о второй части эвекции, просневсисе Птолемея. Дискуссия сошла на нет, когда в 1862 году Шаль вдруг подхватил оружие, выпавшие из рук Седийо, и указал, как ему казалось, на некоторые противоречия в утверждении Птолемея. Никто не ответил на вызов до того, как это сделал Бертран в 1871 году; он обратил внимание на несколько неточностей в тексте Абуль-Вафы, которым мы располагаем сейчас, а также показал, что Абуль-Вафа не прибавил свой «мохазат» к просневсису, так как просневсис не был включен в его «вторую аномалию». У нас нет необходимости вдаваться в дальнейшие подробности спора; но, дабы показать, что любое [228] оружие считалось достаточно хорошим для защиты Абуль-Вафы, можно отметить, что Седийо и Шаль пытались доказать, будто Тихо Браге скопировал свое открытие у Абуль-Вафы, так как называет его hypothesis redintegrata. Браге употребил это же выражение, говоря о собственной планетной системе, о которой самым решительным образом заявлял, что она является его оригинальным открытием, и которую активно защищал от других претендентов. В будущем любой, кто хотел бы приписать открытие Абуль-Вафе, лишится всякой надежды, поскольку этот вопрос к настоящему времени тщательно изучен как математиками, так и востоковедами.

«Альмагест» Абуль-Вафы никогда не опубликовался в полном объеме, однако есть три перевода глав, о которых идет речь, которые отличаются лишь в нескольких мелочах. Ни в одном месте книги он не опережает Птолемея и не утверждает, что сделал какое-либо новое открытие, а, говоря о трех неравенствах, просто делает то же, что и другие арабские астрономы. Он начинает с описания первого (уравнение центра) и второго (эвекция) и указывает, когда они достигают максимумов. Затем он говорит, что мы нашли[233] третье неравенство, которое имеет место, когда центр эпицикла находится между апогеем и перигеем эксцентра, и которое достигает максимума, когда Луна находится примерно в «таслис» или «тасдис» от Солнца, притом что оно нечувствительно в сизигии и квадратуре. Максимум – ?°. Он объясняет, что это вызвано отклонением линии апсид в эпицикле, и совершенно правильно описывает механизм, принятый Птолемеем (имени которого он не называет), допуская, что линия апсид направлена не к Земле, а к другой точке на линии апсид эксцентра. Непредвзятому читателю трудно понять, как можно не увидеть, что Абуль-Вафа просто копирует Птолемея. Седийо утверждал, что слова «таслис» и «тасдис» означают октанты (где вариация достигает максимума); но любой другой востоковед, который высказался по этому поводу, утверждает, что слова, судя по их корням, соответствуют числам 6 и 3, другими словами, элонгациям 60° и 120° от Солнца. Это согласуется с фактами, так как Био на основании числовых данных у Птолемея показал, что отклонение линии апсид достигает максимального значения ±13° 8,9? в элонгациях 90° + 32°57,5?[234]. Но следует признать, что слова, о которых идет речь, также используются очень неопределенно, например, самим Абуль-Вафой, который говорит, что скорость высших планет после выхода из солнечных лучей постепенно уменьшается, пока их расстояние от Солнца не составит примерно «таслис», когда они останавливаются. Это почти выглядит так, будто эти слова могут обозначать любую элонгацию вне сизигии и квадратуры[235].

Если бы Абуль-Вафа действительно сделал открытие, следовало бы ожидать от последующих арабских астрономов каких-либо указаний на него. Но ни один из них не приводит ничего, кроме интерпретаций лунной теории Птолемея, и в таких выражениях, которые очень похожи на использованные у Абуль-Вафы. На этот факт сразу же обратили внимание и привели в пример Исаака Исраэли Толедского (около 1310 г.) и Джабира Севильского[236], хотя, конечно, вполне возможно, что эти два автора оставались в неведении относительно возможного прогресса багдадской школы философии. Но это возражение не относится к Насир ад-Дину ат-Туси, в чьем обзоре «Альмагеста» и «Памятке по астрономии» описаны известные Птолемею неравенства, и никакие другие, и авторство их отдано Птолемею[237]; также и у Махмуда аль-Джагмини (около 1300 г.), написавшего компендиум (мулаххас) астрономии[238]. Нельзя возразить и против слов Абуль-Фараджа (Бар-Эбрея), и невозможно объяснить эффект просневсиса яснее, чем это делает он. Он говорит: «Третье неравенство – угол, образованный в центре эпицикла двумя линиями, которые проведены одна из центра Вселенной, а другая из точки, называемой просневсис, в конце которой находится апогей эпицикла, где начинается собственно движение и которая называется средним апогеем. Апогей, который находится в конце линии, проведенной из центра Вселенной, называется видимым. Точка просневсиса находится на стороне перигея эксцентра в 10 частях 17 минутах от центра мира[239], которая сама находится на том же расстоянии от центра эксцентра. Максимальное значение этого угла составляет 13 частей 9 минут, когда Луна является полумесяцем, или ? серпа, то есть рядом с шестиугольником или треугольником с Солнцем. Когда эпицикл находится в четырех или восьми знаках от апогея эксцентра, Солнце находится в двух или четырех знаках от [центра] эпицикла, то есть на полпути между этим центром и апогеем. В таблицах это неравенство двух апогеев называется первым углом и включается в движение центра»[240]. Здесь мы видим совершенно отчетливое описание птолемеевской системы, и в то же время оно прекрасно согласуется с изложением у Абуль-Вафы. Абуль-Фарадж (как и Насир ад-Дин) даже приводит в качестве четвертого неравенства по долготе то, что вызывается движением по орбите, наклоненной к плоскости эклиптики, так что он не упустил бы описать вариацию, если ее действительно обнаружил багдадский астроном. Можно добавить, что еврейский автор Авраам бар-Хия (1100 г.) в своей Sphaers mundi, «Форме земли», также описывает «аберрацию» эпицикла апсид, главным образом «in sexta et tertia parte mensis»[241].

Следовательно, Абуль-Вафа не знал ничего о движении Луны, кроме того, что заимствовал у Птолемея. Но просневсис Птолемея – не та вариация, которую обнаружил Тихо Браге. Последняя зависит только от элонгации Луны от Солнца, так как она равна + 39,5? sin 2?, тогда как выразить эффект просневсиса без аномалии неподвластно смертному человеку. У Птолемея выражение для всех предполагаемых им неравенств по долготе при разложении содержит, помимо членов, представляющих уравнение центра и эвекцию, причем последняя равна

+ 1°19,5? sin(2? – m),

весьма существенный член

+ 17,8? sin 2? [cos(2? + m) + 2 cos (2? – m)],

где в – это элонгация, am – средняя аномалия. Очевидно, что этот член не имеет ничего общего с вариацией, за исключением того, что он исчезает в сизигиях и квадратурах. Тихо Браге не прибавил свой новый элемент к неизмененной лунной теории Птолемея, да и фактически таким образом мы бы просто исказили его теорию, так что максимальная ошибка достигла бы более чем 3°. По той причине, что Птолемей не располагал достаточными результатами наблюдений, он мог лишь исходить из того, что и после учета эвекции остаются некоторые весьма заметные неравенства, проявляющиеся только вне сизигий и квадратур, но он не смог найти закон, управляющий этим явлением, и не знал, насколько большую величину оно представляет; он мог только слегка корректировать свои построения, и в этом за ним самым добросовестным образом следовали арабы, которые ничего не прибавили к сделанному им и предоставили обнаружить третье лунное неравенство человеку, кому суждено было вдохнуть новую жизнь в практическую астрономию.

Переходя к пяти планетам, мы находим, что, вообще говоря, арабы предприняли очень мало попыток усовершенствовать работу Птолемея. Однако они не удовольствовались использованием системы Птолемея исключительно в качестве вспомогательного геометрического способа вычислений; им нужна была реальная, физически истинная система мироздания, и потому они принимают на веру существование твердых хрустальных сфер на манер аристотелевских. Над Луной находится аль-афир, пятая сущность, лишенная легкости и тяжести и не воспринимаемая человеческими чувствами; из этого вещества образуются сферы и планеты (Аль-Баттани). Уже в книге Аль-Фергани мы находим принцип, который, как мы видели, появляется еще в V веке (Прокл) и становится общепризнанным в Средние века, гласящий, что наибольшее расстояние до планеты равно наименьшему расстоянию до планеты, расположенной сразу же над ней, таким образом, что между сферами не остается пустых пространств[242]. По Аль-Фергани, полудиаметр Земли равен 3250 милям, что почти соответствует 56? мили Аль-Мамуна вплоть до градуса, если принять ? = ²²/₇. Исходя из расстояний до Луны и Солнца у Птолемея, легко выразить другие расстояния в полудиаметрах Земли, так как соотношение между максимальным и минимальным расстояниями хорошо вписывается в теорию Птолемея. Аль-Баттани приводит аналогичный ряд цифр, хотя и с некоторыми небольшими различиями. Он умалчивает о том, как своеобразно трактовал Птолемей теорию Меркурия. В приведенной ниже таблице указаны расстояния в полудиаметрах Земли:

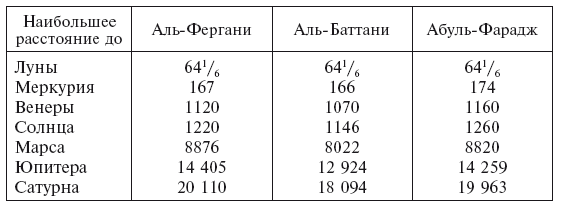
Аль-Кушчи, один из астрономов Улугбека, приводит перечень полудиаметров «углублений» планетных сфер (то есть наименьших расстояний), выраженных в парасангах, причем диаметр Земли составляет 2545 парасангов. Выраженные в полудиаметрах Земли, цифры несколько отличаются от приведенных выше, например, наименьшее расстояние до Солнца составляет 1452, а наибольшее до Сатурна – 26 332, но он ничего не сообщает о том, как были найдены эти значения.

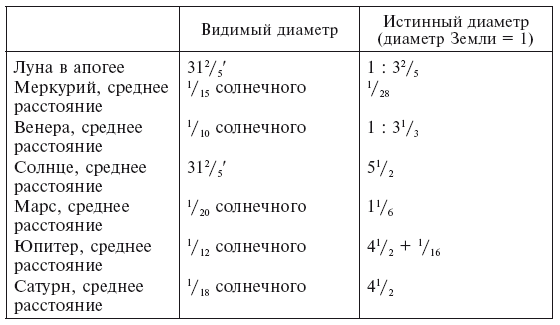
Перед тем как оставить эту тему, приведем диаметры планет по Аль-Фергани, так как они стали известны в Европе очень рано и на них ссылались Роджер Бэкон и другие[243]. При несущественных различиях Аль-Баттани, Абуль-Фарадж и Авраам бар-Хия приводит одни и те же цифры:

Система сфер наиболее подробно изложена в трех более поздних трактатах: космографии Закарии ибн Мухаммада ибн Махмуда аль-Казвини (около 1275 г.), астрономии Абуль-Фараджа, написанной в 1279 году, и астрономии Махмуда ибн Мухаммада ибн Омара аль-Джагмини, о котором одинаково неизвестно, когда он жил и кто был по национальности, но, вероятно, он писал в XIII или XIV веке. В этих учебниках мы находим сложную систему сфер, которая должна была учитывать все особенности движения планет в полном согласии друг с другом в общем порядке сфер, но не предложила ничего нового в теории Луны и других планет. Прилагаемые рисунки (взятые из Аль-Джагмини) лучше проиллюстрируют идеи, чем длинное описание[244].

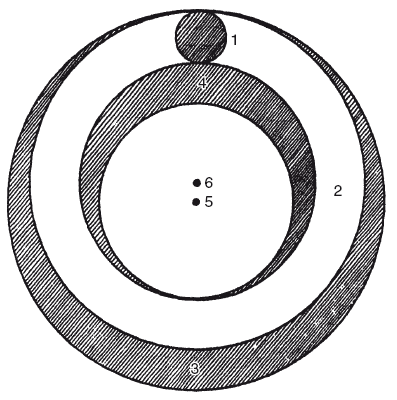
1 – Солнце; 2 – эксцентрическая сфера; 3 — окружающая сфера; 4 – комплемент окружающей сферы; 5 – центр мира; 6 — центр эксцентрической сферы

Солнце представляет собой сплошное шарообразное тело между двумя эксцентричными сферическими поверхностями, которые касаются двух других поверхностей, в общем центре которых находится Земля и которые между собой заключают пространство (или междусферие, как называет его Абуль-Фарадж), названное у Аль-Джагмини аль-муматталь, или равновращающаяся сфера, которая совершает то же движение с запада на восток, что и неподвижные звезды, то есть имеется в виду прецессия. Сферы трех внешних планет и Венеры изображены на том же плане, за исключением того, что место тела Солнца занимает сфера-эпицикл каждой планеты, на внутренней поверхности которой прикреплена планета (сплошное шарообразное тело), или (как говорит Абуль-Фарадж) «вставлена, как жемчужина

в кольце, касаясь поверхности в одной точке». Ось эксцентрической сферы наклонена к оси сферы аль-муматталь, что вызывает смещение по широте. Лунная система включает в себя дополнительную сферу за пределами других, центр которой совпадает с центром мира и которая называется аль-джавзахар, что означает созвездие Дракона, так как эта сфера обеспечивает обращение лунных узлов («головы и хвоста дракона») по зодиаку[245]. Внутренняя из двух концентрических сферических поверхностей, между которыми лежит эксцентрическая сфера, непосредственно окружает огненную сферу Земли. Система Меркурия сложнее, так как должна предусматривать пространство для вращения центра эксцентрической сферы. На рисунке показана эксцентрическая сфера, заключенная в сферу, аль-мудир, или вращающаяся, которая позволяет верхней апсиде или апогею эксцентра или деферента (3 на рисунке) двигаться вправо по наружной сфере аль-мудир. Внутренняя поверхность сферы аль-муматталь непосредственно окружает сферу аль-джавзахар Луны.

Необходимым следствием принятого Птолемеем большого солнечного параллакса в У было то, что Меркурий и Венера оказались на очень близком расстоянии от Земли, так как считалось, что они ближе, чем Солнце. Так, Авраам бар-Хия говорит, что тень Земли простирается за пределы орбиты Меркурия, но не доходит до Венеры. Птолемей никогда не говорит о параллаксах Меркурия и Венеры, о которых ничего не было известно, хотя, конечно, они должны были быть больше 3?. Но исходя из того, что наименьшее расстояние до Меркурия равно расстоянию до Луны в апогее, параллакс Меркурия должен вырасти до 54?, а такое значение наверняка показалось бы слишком большим, хотя, кажется, Аль-Баттани не нашел в нем ничего странного, возможно, потому, что Меркурий не виден в момент нижнего соединения. Быть может, именно большой параллакс Меркурия побудил Ибн Юнуса (без каких-либо объяснений) уменьшить солнечный параллакс с 3 до 2? или, вернее, до 1 ?57?.

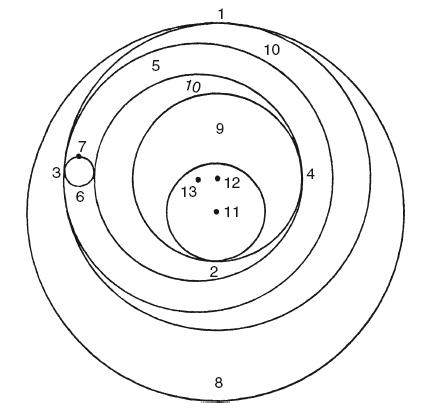
Сферы Меркурия

1 — верхняя апсида; 2 – нижняя апсида; 3 — верхняя апсида деферента; 4 — нижняя апсида деферента; 5 – деферент; 6 — эпицикл; 7 – Меркурий; 8 — окружающий комплемент; 9 — окруженная часть сферы аль-муматталь; 10 — сфера аль-мудир; 11 — центр мира; 12 – центр аль-мудир; 13 — центр деферента

Джабир упрекает Птолемея за то, что тот назвал параллаксы планет несущественными, и замечает, что логически он должен был в таком случае поместить Венеру и Меркурий над Солнцем. Он прилагает большие усилия, чтобы показать, что Венера может находиться точно на линии, соединяющей Солнце и Землю. Фактически Джабир не упускает ни единой возможности раскритиковать методы Птолемея для нахождения элементов орбит[246] и, как правило, очень несправедлив по отношению к греческому ученому, хотя и не рискует заменить систему Птолемея на какую-либо иную и не возражает против ее общих принципов[247].

Попытки Джабира выискать недостатки в работе Птолемея, пожалуй, были связаны с быстрым ростом популярности аристотелевской философии в Испании XII века, и, хотя этот процесс продлился недолго, все же он сыграл значительную роль в распространении трудов Аристотеля в христианском мире, а также создал ореол вокруг Кордовского халифата, который в ту эпоху просвещенного правления Альмохадов, казалось, возродил славу золотых дней мусульманского мира. Три имени особым образом связаны с этим течением: Абу Бекр Мухаммад ибн Яхья ас-Саиг, называемый ибн Баджа (Сарагоса, умер в 1139 г.), известный среди схоластов под именем Авемпас; его ученик Мухаммад ибн Абдул-Малик ибн Туфайль (Гранада, умер в 1185—1186 г.), Абубацер у схоластов; и, наконец, величайший философ ислама Абуль-Валид Мухаммад ибн Рутттд, известный как Аверроэс (1126—1198). Изучая Аристотеля, они обращали особое внимание на его научные труды и, в отличие от своих христианских преемников, не пренебрегали всем остальным, кроме диалектики. Поэтому арабским философам казалось необходимым принять систему гомоцентрических сфер или какую-то ее модификацию, и, разумеется, это заставило их отказаться от теории эпициклов. То малое, что нам известно о взглядах Ибн Баджи по этому вопросу, можно найти в известном труде «Путеводитель растерянных» великого еврейского ученого Моше бен Маймона из Кордовы, более известного под именем Маймонид, который говорит нам, что получил свои сведения от ученика Ибн Баджи. Как и Джабир (с чьим сыном он был знаком), Маймонид сомневался, что Меркурий и Венера ближе к Земле, чем Солнце, хотя не рисковал сказать, как они на самом деле движутся. Но, что еще важнее, он объявил, что движение планеты на эпицикле противоречит принципам физики, потому что в этом мире возможны только три движения: вокруг его центра, к нему или от него; в то же время он утверждал, что, по Аристотелю, круговое движение может совершаться только вокруг реального центрального тела. Хотя Аристотель на самом деле не возражает против эпициклического движения с центром в математической точке по той простой причине, что, когда он писал, оно еще не было предложено, притом что, как мы уже видели, его принцип движения не имел ничего общего с центром движения, легко понять, что перед Ибн Баджей в действительности стояла та же проблема, которая впоследствии породила столько препятствий на пути развития науки в Европе: если чего-то нет в книгах Аристотеля, значит, это недостойно внимания. Согласно Маймониду (который, однако, делает оговорку, что он не слышал этого от учеников), Ибн Баджа создал собственную систему, в которой допустил только эксцентры, но не эпициклы. Он ничего не сообщает об этой системе, но вряд ли можно сомневаться, что ее автор ограничился общими фразами и не пытался отобразить в ней таких явлений, как лунные неравенства. Маймонид замечает, что своей реформой Ибн Баджа ничего не добился, ведь гипотеза эксцентров вызывает такие же возражения, как и гипотеза эпициклов, поскольку она также предполагает движение вокруг воображаемой точки вне центра Земли. Центр эксцентра, на котором должно двигаться Солнце, находится вне выпуклости лунной сферы и внутри вогнутости сферы Меркурия; центры движения Марса и Юпитера находятся между сферами Меркурия и Венеры, а центр эксцентра Сатурна находится между сферами Марса и Юпитера. Он добавляет, что вращение ряда концентрических сфер вокруг общей оси вполне возможно, но не вращение вокруг разных осей, наклоненных друг к другу, поскольку сферы будут мешать друг другу, если только между ними нет других сферических тел. Таким образом, эта попытка возродить и видоизменить систему (подвижных?) эксцентров ничего не исправила[248].

Ибн Туфайль, второй из трех мусульманских философов Испании, визирь и врач при дворе эмира Марокко Юсуфа Ибн Абдул-Мумина, видимо, пошел по стопам своего учителя; однако его единственная сохранившаяся работа, своего рода религиозно-мистический роман об освобождении души от оков материального мира, не дает ключа к его идеям относительно системы планет. Но Ибн Рушд, который также возражает против эксцентров и эпициклов, говорит в своем комментарии к «Метафизике» Аристотеля, что у Ибн Туфайля были великолепные теории по этому вопросу; а ученик Ибн Туфайля астроном Аль-Битруджи во введении к своей теории планет говорит о нем: «Известно, что знаменитый судья Абу Бекр ибн Туфайль сказал нам, что открыл астрономическую систему и принципы различных движений, отличную от той, что установлена Птолемеем, без эксцентров и эпициклов, которая без ошибок представляет все движения планет». То есть Ибн Туфайль, вероятно, был настоящим автором довольно сложной системы, разработанной и оставленной нам его учеником в труде о планетах, который в следующем веке был переведен на иврит, а с иврита на латынь и опубликован в 1531 году[249].

Цель этой системы заключалась в том, чтобы объяснить устройство Вселенной как оно есть на самом деле, а не только в том, чтобы геометрически представить движения планет, дабы иметь возможность предсказывать их положение на небе в любой момент времени; и автор (будь он Ибн Туфайль или Аль-Битруджи, он же Альпетрагий) особо подчеркивает, что не имеет намерения ни проверять ее путем сравнения с наблюдениями, ни учитывать мелких деталей этих движений. Основная идея заключается в гомоцентрических сферах, каждая звезда прикреплена к сфере, а движущей силой является девятая сфера, находящаяся за пределами сферы неподвижных звезд. Таким образом, испанскому философу следовало удовлетвориться системой Евдокса или ее модификацией, сделанной Аристотелем (которого он никогда не называет по имени, а лишь «мудрецом»), но, к сожалению, он зациклился на идее, что перводвигатель повсюду должен производить только движение с востока на запад, и поэтому ему пришлось отказаться от независимого движения планет с запада на восток и вернуться к старой идее ионийцев о семи планетах, которые просто совершают суточное вращение несколько медленнее, чем неподвижные звезды. Истинная скорость перводвигателя немного больше; восьмая сфера совершает оборот за несколько более длительный период (24 часа), и эффект перводвигателя постепенно ослабевает с увеличением расстояния, пока мы не доходим до сферы Луны, самой отдаленной от перводвигателя, которой на полный оборот требуется почти двадцать пять часов. Это была старая, примитивная идея ионийской школы, но Аль-Битруджи (или его учитель) увидел, что этого недостаточно, так как не только полюс эклиптики отличается от полюса экватора, что не дает планетам перемещаться по замкнутым орбитам, но и, более того, планеты не находятся на одинаковом расстоянии от полюса эклиптики и у каждой свое движение по широте и переменная скорость по долготе; и все это еще нужно учесть. Девятая сфера обладает только одним движением, но восьмая – уже двумя: по долготе (прецессия) и тем, которое вызывает полюс эклиптики, описывающий небольшой круг вокруг среднего положения, тем самым создавая гипотетическое колебание или трепет равноденствий. Точно так же полюс каждой планеты описывает небольшой круг вокруг среднего положения (то есть полюса эклиптики), тем самым производя неравенства по долготе и широте движения. Всякий раз, когда фактический полюс планетной орбиты находится на параллели среднего полюса, очевидно, что планета совершает свой суточный оборот со средней скоростью, в то время как скорость увеличивается или уменьшается, когда фактический полюс находится соответственно на минимальном или максимальном расстоянии от полюса небес (движение полюса орбиты прибавляется или вычитается из движения планеты), так что эпицикл тем самым оказывается излишним. Длины радиусов этих малых кругов не приводятся, кроме как для Сатурна, для которого радиус составляет 3°3?, тогда как средний полюс Луны находится в 5° (наклон лунной орбиты) от полюса эклиптики, и малый круг настолько мал, что не производит попятного движения, что также имеет место в случае Солнца. Для периодов полюсов внешних планет приведены следующие цифры. Сатурн делает 57 оборотов за 59 лет и 1? + ? дня, за этот период средний полюс отстает на 2 оборота и 1?° + ²/₉°. Юпитер делает 65 оборотов за 71 год, средний полюс отстает на 6 оборотов. Марс делает 37 оборотов за 79 лет и 3¹/₆ + ¹/₁₅ дня, полюс отстает на 42 оборота и 3¹/₆°.

Другими словами, движения на этих малых кругах совершаются за синодические периоды планет. Аналогично полюс Венеры совершает 5 оборотов за 8 лет минус 2? дня + ¹/₂₆ отставая на 1⁵/₈ оборота в год; а Меркурий – 145 оборотов за 46 лет и 1 V 30 дня. Любопытно, что Аль-Битруджи меняет порядок планет, помещая Венеру между Марсом и Солнцем, потому что defectus (отставание) Венеры меньше, чем у Солнца. Он также говорит, что никто не привел каких-либо веских оснований для принятия привычного порядка планет и что Птолемей ошибается в том, что Меркурий и Венера никогда не выстраиваются в одну линию с Солнцем (об этом уже говорил Джабир); и так как они светятся собственным светом, то не будут выглядеть темными пятнами, проходя между Землей и Солнцем. А то, что они не получают свет от Солнца, по его мнению, доказывается тем фактом, что мы никогда не видим их серпообразными.

Нам нет нужды подробнее останавливаться на этой причудливой теории спирального движения, как ее ошибочно называли[250]. Она представляла собой громадный шаг назад, совершенно неоправданный, поскольку теория не могла всерьез претендовать на превосходство над системой Птолемея, вся сложность которой объясняется тем, что она старалась учитывать все известные подробности нерегулярного движения светил, но при этом ее можно сделать очень простой, если цель состоит лишь в представлении основных явлений. От еврейского астронома из Толедо Исаака Исраэли мы узнаем, что новая система произвела большую сенсацию, но оказалась недостаточно разработанной, чтобы ее приняли всерьез, и что она не могла заменить собой систему Птолемея, основанную на самых строгих расчетах[251]. Другой еврейский автор – Леви бен Гершом в книге, написанной в 1328 году, дал пространное опровержение гипотезы Аль-Битруджи. Однако последний, безусловно, представляет общее стремление испанских приверженцев Аристотеля преодолеть трудности физического характера в системе Птолемея; так, Ибн Рушд говорит, что астрономия Птолемея не более чем удобный метод расчета и что сам он в юности надеялся подготовить трактат по данному вопросу.

Пока на крайнем Западе предпринимались безрезультатные попытки разработать новую астрономическую теорию, астрономы Востока не оставались слепы к необходимости найти такую систему, в которой планеты без опоры в пространстве не совершали бы столь немыслимо сложных движений; и в XIII веке мы видим, что один из самых выдающихся арабских астрономов – Насир ад-Дин ат-Туси выступает в пользу системы сфер, которую считает более приемлемой, чем систему эксцентров и эпициклов. В дополнение к обзору или краткому изложению «Синтаксиса» Птолемея он написал короткую работу под названием «Памятка по астрономии», где в разных фрагментах выражает недовольство системой Птолемея. В главе о Луне (на которую мы уже ссылались) он перечисляет различные аномалии, среди которых упоминает аномалию светимости, то есть пятна на Луне, которые, по его мнению, вызваны другими небесными телами, движущимися в лунном эпицикле и неодинаково освещенными светом Луны. Затем он говорит, что простая теория должна содержать центр эпицикла, описывающий за равные промежутки времени равные дуги на деференте, и диаметр эпицикла, соединяющий перицентр и апоцентр, указывая на центр деферента. Однако ни одно из этих условий не выполняется. Против теорий планет он выдвигает те же возражения, которые, надо сказать, весьма справедливы, так как введение экванта было совершенно неестественным приемом. Однако это ничто по сравнению с тем искусственным механизмом, который придумал Птолемей, чтобы учесть движения пяти планет по широте, особенно Меркурия и Венеры. Насир ад-Дин ат-Туси описывает поразительно сложные движения деферентов и эпициклов этих планет и отмечает, что они «требуют введения системы направляющих сфер, о которых древние ничего не говорят». Затем, в следующей главе, он объясняет свою собственную систему, которая позволяет отбросить эти комбинации.

Сначала он доказывает, что, если в одной плоскости расположены два круга, один касающийся другого с внутренней стороны и имеющий диаметр, равный половине диаметра второго круга, и если больший круг вращается и некая точка движется по окружности меньшего круга в противоположном направлении со скоростью вдвое больше и начиная от точки соприкосновения, тогда эта точка будет двигаться по диаметру большего круга[252]. Итак, теперь мы можем предположить, что эти два круга являются экваторами двух сфер, а точку заменить сферой, представляющей эпицикл Луны (1 на рисунке). Насир ад-Дин далее вводит еще одну сферу (2), окружающую эпицикл и предназначенную для того, чтобы удерживать на месте диаметр от апогея до перигея, всегда совпадающий с диаметром сферы (4); «придадим ему подходящую толщину, но не слишком большую, чтобы не занимать слишком много места». Затем он вводит еще две сферы, одна из которых (3) соответствует меньшей сфере в приведенной выше гипотезе, и ее диаметр равен расстоянию от центра деферента до центра Земли в системе Птолемея; а другая сфера (4) имеет диаметр в два раза больше. Наконец, (4) помещается внутри несущей сферы (5), концентрической с миром и занимающей вогнутость сферы (6), экватор которой находится в плоскости орбиты Луны. (2), (4) и (5) обращаются за тот же период, за который центр эпицикла совершает оборот; (3) обращается за половину этого времени, а (6) обращается в противоположную сторону с той же скоростью, что и апогей эксцентра. Рисунок изображает, как эпицикл перемещается взад-вперед по диаметру (4) и во время обращения круга (5) описывает замкнутую кривую, о которой Насир ад-Дин справедливо говорит, что она несколько напоминает круг, но на самом деле им не является, по какой причине не может служить идеальной заменой эксцентрической окружности Птолемея. По его оценке, наибольшая разница между положениями Луны, проистекающими из этих двух теорий, составляет ¹/₆° градуса, посередине между сизигией и квадратурой. За исключением действия направляющей сферы (2), кривую, напоминающую круг, описывал бы не центр эпицикла, а точка соприкосновения окружностей (3) и (4). Тот же метод можно применить к Венере и трем внешним планетам, и Насир ад-Дин обещает изложить новую теорию Меркурия в приложении, но оно, видимо, утеряно.

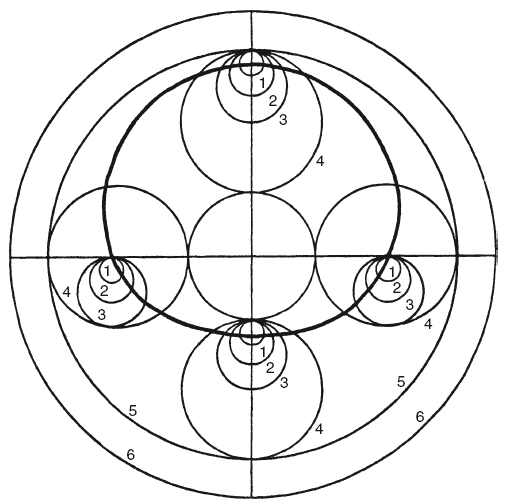
Жирная линия не образует круг. Все остальные фигуры – круги

Насир ад-Дин также старается улучшить предложенный Птолемеем механизм, дабы проиллюстрировать, каким образом эпицикл остается параллелен плоскости эклиптики. Он говорит, что знаменитый Ибн аль-Хайсам (впоследствии получивший признание на Западе под именем Альхазен, автор известного труда по оптике) написал об этом главу, прибавив к каждому эпициклу две сферы, чтобы учесть наклон диаметра перигея-апогея, и еще две для нижних планет для диаметра под прямым углом к нему[253]. Насир ад-Дин использует тот же принцип, которым руководствовался в демонстрации движений по долготе, и показывает, что в этом случае с помощью двух сфер можно заставить крайние точки диаметра эпицикла двигаться взад-вперед по дуге сферы[254].

Он утверждает, что эта схема лучше птолемеевской тем, что не вводит ошибок по долготе[255], но признает, что он не сумел избавиться от серьезного возражения против вспомогательной окружности Птолемея, а именно что неравномерное движение по долготе относительно центра деферента требует введения соответствующей неравномерности в движение на вспомогательной окружности, так чтобы движение было равномерным по отношению к экванту. Насир ад-Дину не хватило изобретательности, чтобы найти такое расположение сфер, которое бы могло устранить такую необходимость.

Таким образом, все попытки взбунтоваться против птолемеевской системы окончились неудачей. И они не заслуживали ничего иного, поскольку невозможно было найти ничего лучшего системы Птолемея, пока не стало ясно, что Птолемей ошибался не в математических методах, которые были совершенны, а в самой фундаментальной идее неподвижно покоящейся Земли. По-видимому, еще не пришло время для радикальных перемен в этом вопросе. Хотя арабские авторы не рассматривали учения о движении Земли, у нас есть свидетельства того, что они знали о гипотезе ее суточного вращения, что было естественным следствием их знакомства с античными мыслителями. Один из соработников Насир ад-Дина по обсерватории в Мераге Али Наджмуддин аль-Катиби, умерший в 1277 году, написал книгу по философии «Хикмет аль-айн», где выступает против этого мнения, которое приписывает «некоторым философам». «В качестве опровержения, – говорит он, – я не утверждаю, что если бы это было так, то птица, летящая в одну сторону с движением Земли, не смогла бы ее догнать, ведь Земля двигалась бы гораздо быстрее птицы, так как за сутки она возвращается на прежнее место. Этот довод не убедителен, ибо можно было бы возразить, что атмосфере вблизи Земли сообщается ее движение, как и эфиру сообщается движение небесной сферы. Но я отвергаю эту теорию, потому что все движения на Земле совершаются по прямой линии, поэтому мы не можем согласиться с тем, что Земля движется по кругу»[256].

На какую реформацию астрономии можно было надеяться, пока в ходу были подобные аргументы? Из этого замечания Аль-Катиби нам непонятно, действительно ли были какие-то арабские философы, верившие во вращение Земли. Однако в «Зоаре», великом каббалистическом труде, приписываемом Моше бен Шем Тов де Леону (умер в 1305 г.), говорится, что некий раввин Амнон Старший (иначе неизвестный) учил, будто «Земля крутится, как шар, вокруг самой себя, и есть люди с верхней стороны, а есть с нижней». Хотя этот отрывок, как и некоторые другие в «Зоаре», возможно, является гораздо более поздней вставкой, все-таки мы не очень удивились бы тому, что некоторые образованные иудеи находились под влиянием взглядов Гераклита, поскольку установлено, что доктрины каббалистов были тесно связаны с поздней греческой философией. Но так или иначе из этого единичного случая ничего не вышло, и суточное вращение небес по-прежнему везде считалось общепризнанным и самоочевидным фактом.

Таким образом, арабские астрономы, которые действительно хотели детально проследить движения небесных тел, должны были принимать систему Птолемея в целом. Уже давно была осознана необходимость в новых планетных таблицах, и этот важный труд наконец предприняли король Кастилии Альфонсо X и несколько еврейских и христианских астрономов, работавших при его правлении в Толедо, которые и подготовили знаменитые «Альфонсовы таблицы». По всей видимости, у короля были некоторые сомнения по поводу истинности системы с точки зрения физики, судя по его знаменитому высказыванию о том, что, если бы во время сотворения мира Бог посоветовался с ним, он дал бы ему хороший совет. Таблицы были подготовлены под руководством еврея Исхака бен Саида, называемого Хасаном, и врача Йегуды бен Моше Коэна и закончены в 1252 году, когда Альфонсо взошел на трон Кастилии. Они пользовались прекрасной репутацией на протяжении трехсот лет как превосходнейшие планетные таблицы; впервые их напечатали в 1483 году, но еще задолго до того они распространились по всей Европе в многочисленных рукописных копиях, многие из которых сохранились до наших дней. В пятитомном мадридском издании 1863—1867 годов Libros del Saber de Astronomia del Rey D. Alfonso X. de Castella, «Книги астрономических знаний короля Кастилии Альфонсо X», подсчитано двадцать шесть кодексов. Этот сборник, включающий в себя ряд глав о сферической и теоретической астрономии с последующими таблицами, видимо, составлен из нескольких рукописей, поскольку там много раз повторяются даже самые элементарные вопросы. В третьем томе рассматриваются теории планет, но тщетно было бы искать там какие-либо усовершенствования птолемеевской системы; напротив, он как нельзя лучше иллюстрирует плачевное состояние астрономии в Средние века. В основном элементы орбит повторяют птолемеевские, порой приводятся только приблизительные данные, а между разными главами есть расхождения в некоторых величинах. Хотя Птолемей помещает центр деферента на полпути между центром экванта и Землей, Libros del Saber помещают центр экванта (cerco del alaux[257]) на полпути между Землей и центром деферента (cerco del levador), как в птолемеевской теории Меркурия, которую авторы, видимо, распространяют и на другие планеты, опуская движение центра деферента по небольшой окружности; но тем не менее они верно приводят его для Меркурия[258]. Там мы видим весьма любопытный рисунок деферента Меркурия в виде эллипса (его оси относятся друг к другу примерно как 6 к 5), причем в центре находится нечто похожее на Солнце. Эта кривая построена из ряда небольших дуг, и, очевидно, это не что иное, как кривая, описываемая центром эпицикла Меркурия в теории Птолемея. Ибо, согласно этой теории, центр деферента описывает окружность небольшого круга с радиусом равным ¹/₂₁ радиуса деферента в направлении с востока на запад, в то же время когда центр эпицикла обходит по окружности деферента с запада на восток. Это заставляет центр эпицикла описывать замкнутую кривую, напоминающую эллипс, оси которого находятся в отношении 11:10, почти как на испанском чертеже, и, следовательно, последний отнюдь не является каким-то открытием, предвосхитившим великое открытие Кеплера, так как в случае нижних планет реальной орбитой является эпицикл[259]. Маленький похожий на Солнце объект в центре эллипса представляет центр малого круга у Птолемея, и он либо был вставлен в рукопись через несколько веков после ее написания, либо, что вернее, это всего лишь небольшое расплывшееся пятнышко туши на пергаменте в том месте, где неподвижная ножка циркуля оставила дырочку. Овальный деферент Меркурия встречается в нескольких книгах, опубликованных в XVI и XVII веках[260].

Если бы этот несколько запутанный сборник эссе под названием Libros del Saber опубликовали в XIII веке, он бы не продвинул вперед астрономическую науку, но тем не менее нельзя отрицать, что «Альфонсовы таблицы» в свое время принесли большую пользу. Правда, в них не приводятся фактические элементы и ничего не говорится о каких-либо наблюдениях, с помощью которых были установлены несколько более правильных значений средних движений[261].

Закончив наш обзор планетных теорий арабов, мы должны добавить еще несколько слов об их идеях о природе и движении сферы неподвижных звезд. Преувеличенные понятия, бытовавшие до изобретения телескопа, о видимых угловых диаметрах звезд, естественно, привели к ошибочным оценкам их фактического размера, основанным на предположении, что сфера неподвижных звезд (восьмая) находится непосредственно за сферой Сатурна[262]. Предполагалось, что звезды первой величины имеют видимый диаметр, равный ¹/₂₀ видимого диаметра Солнца, из чего следовало, что их фактические диаметры примерно в 4? раза больше, чем у Земли, или приблизительно равны диаметрам Юпитера и Сатурна; тогда как диаметры звезд шестой величины примерно в 2? раза больше, чем у Земли, или примерно вдвое больше, чем у Марса[263]. Что касается природы звезд, то, похоже, они в основном считались самосветящимися сгущенными частями сферы, хотя Авраам бар-Хия говорит, что восьмая сфера светится не равномерным светом, а имеет более плотные пятна, которые освещаются Солнцем и кажутся нам неподвижными звездами[264].

Чтобы объяснить видимое медленное смещение звезд, параллельное эклиптике, с запада на восток, в результате чего растет их долгота, а широта остается неизменной, возникла необходимость ввести девятую сферу (перводвигатель), которая поворачивается за двадцать четыре часа и сообщает это движение восьмой сфере, в то время как восьмая крайне медленно вращается вокруг своей оси, образующей угол 23°35? с осью девятой[265]. Однако многие арабские астрономы усложняли простой феномен прецессии тем, что полагали его переменным. Выше (в главе 9) мы уже упоминали, что, как говорят Теон и Прокл, некоторые астрономы до Птолемея, по-видимому, считали, что прецессионное смещение звезд не является поступательным, но ограничивается колебаниями по дуге 8°, по которой перемещаются точки равноденствия взад-вперед по эклиптике, всегда с одной и той же скоростью 1° за 80 лет. По-видимому, абсурдность внезапного изменения направления стала очевидной, как только арабы начали развивать астрономию, ибо мы находим, что один из самых ранних астрономов – Сабит Ибн Курра заменил ее теорией, которая с точки зрения физики вызывает меньше возражений[266]. Он представил себе неподвижную эклиптику (в девятой сфере), которая пересекает экватор в двух точках (средние равноденствия) под углом 23°33?30?, и подвижную эклиптику (в восьмой сфере), зафиксированную на двух диаметрально противоположных точках на окружностях двух малых кругов, центры которых находятся в средних равноденствиях и радиусы равны 4°1843?. Подвижные точки тропиков Рака и Козерога никогда не покидают фиксированной эклиптики, но движутся взад-вперед в пределах 8°37?26?, тогда как две точки на подвижной эклиптике в 90° от точек тропиков движутся по окружностям малых кругов, так что подвижная эклиптика поднимается и опускается на неподвижной, в то время как точки пересечения экватора и подвижной эклиптики приближаются и удаляются в пределах 10°45? в обе стороны. Это движение восьмой сферы, общее для всех звезд, и, следовательно, Солнце иногда будет достигать максимального склонения в Раке, а иногда в Близнецах. Сабит не говорит, что наклонение эклиптики является переменной величиной, и, возможно, ему не приходило в голову, что это неизбежно следовало из его теории; он лишь замечает перемену направления и количества движения равноденствий, которое, по его словам, возросло со времен Птолемея, когда оно составляло всего 1° за 100 лет, в то время как последующие наблюдатели нашли его равным 1° за 66 лет. Таким образом, ошибочное значение у Птолемея в основном и было причиной долгожительства воображаемой теории. Следует отметить, что Сабит выражается довольно сдержанно и, кажется, считает, что нужны дальнейшие наблюдения, чтобы решить, верна теория или нет. Его младший современник Аль-Баттани еще более осторожен; хотя он и повторяет рассказ о «трепете равноденствий» из Теона (о котором говорит, что Птолемей «в своей книге ясно сказал»), но не использует его, а просто принимает значение 1° за 66 лет (или 54,5? в год), которое находит путем сравнения собственных наблюдений и некоторых сделанных Менелаем. В отказе от ошибочного значения у Птолемея, которое принимал только Аль-Фергани, за Аль-Баттани последовал Ибн Юнус, который подошел еще ближе к истине, приняв значение 1° за 70 лет, или 51,2? в год, и который не говорит о трепете. Это в значительной степени заслуга ряда других арабских авторов, что они не позволили сбить себя с толку этим воображаемым явлением; среди них Ас-Суфи, автор единственной уранометрии Средних веков, который следовал за Аль-Баттани, а также Абуль-Фарадж и Аль-Джагмини[267], тогда как Насир ад-Дин упоминает о трепете, но, кажется, сомневается в его реальности. Другие охотно принимали его на веру, например Аз-Заркали, у которого период колебаний 10° в любую сторону равен 2000 мусульманским годам (или 1940 григорианским годам, то есть 1° за 97 лет, или 37? в год). Движение совершается в круге радиусом 10°, в хиджру подвижное равноденствие находилось в 40? увеличивавшейся прецессии, а в 1080 году – в 7°25? [268]. Уменьшение наклона эклиптики, которое обнаружили астрономы Аль-Мамуна, равное 23°33?, безусловно добавило достоверности идее трепета, и следующим шагом в развитии этой любопытной теории стало сочетание поступательного и колебательного движения. Аль-Битруджи, излагающий своего рода историю теории начиная с мифического Гермеса, утверждает, что Теон (или Таун Александрийский, как он его называет) соединил движение на 1° за 100 лет с колебанием[269]. Век спустя это было сделано в действительности, и последний шаг в развитии теории сделал король Альфонсо или его астрономы, которые считали, что равноденствие отступило гораздо дальше, чем позволяла теория Сабита. Было предположено, что равноденствия обходят небеса за 49 000 лет (годовое движение равно 26,45?), в то время как период неравенства трепета составляет 7000 лет, так что в некий Большой юбилейный год все снова станет таким, каким было вначале[270]. Поступательное движение принадлежит девятой сфере, годовая прецессия колеблется в пределах 26,45? ± 28,96?, или от +55,41? до —2?51[271]. Тогда встала необходимость предположить существование десятой сферы, которая как перводвигатель сообщала бы суточное вращение всем остальным, в то время как девятая производила бы поступательное, а восьмая – периодическое движение на малых кругах, находящихся «в вогнутости девятой сферы». Это была легкая и приятная теория благодаря продолжительным периодам и медленным изменениям, которые она производила в величине годовой прецессии; и, не обращая внимания на то, что теория не имеет под собой никаких оснований, кроме того факта, что наклон эклиптики теперь был примерно на 20? меньше, чем заявлено у Птолемея, и что он указал величину прецессии 36? в год, а не около 50?, и часто закрывая глаза на некоторые необходимые следствия из этого, как, например, изменение широты звезд[272], астрономы продолжали принимать эту теорию, пока наконец человек, реально наблюдавший звезды, не встал и не разделался с ней, показав, что наклон эклиптики неуклонно уменьшался и что величина годовой прецессии никогда не изменялась. Мы говорим об этом сейчас только потому, что это потребовало перестановки сфер, и потому, что это было в высшей степени характерно для эпохи, когда не велось никаких постоянных наблюдений и практически не предпринималось попыток улучшить теории Птолемея. Теория трепета – trepidatio или titubatio, как ее иногда называют, была такой единственной попыткой, и лучше было ее вообще не совершать. Однако она стала небезынтересной главой в истории астрономии.

Здесь мы завершаем наш обзор восточной астрономии. Мы опустили несколько ценных вкладов арабских ученых в науку, так как они не связаны с космологией или теорией планет и потому не относятся к рассматриваемым вопросам. Но даже с учетом такого ограничения мы достаточно показали, что, когда европейцы вновь занялись наукой, они нашли астрономию практически в том же состоянии, в котором ее оставил Птолемей во II веке. Однако арабы вложили в их руки мощный инструмент тем, что заменили исчисление хорд у Птолемея на исчисление синусов и тригонометрию и тем самым сыграли чрезвычайно важную роль в дальнейшем развитии астрономии.