Книга: История астрономии. Великие открытия с древности до Средневековья

Глава 8 Размеры мира

Глава 8

Размеры мира

Чтобы перейти от Гиппарха к следующему астроному, чьи представления о порядке и устройстве мира нам предстоит рассмотреть, мы должны преодолеть более двух с половиной столетий. Это дает нам удобную возможность собрать в одном месте взгляды древних на величину Земли и расстояния до планет, которые мы время от времени затрагивали лишь вскользь.

С эпохи Платона шарообразную форму Земли не оспаривал ни один философ, за исключением последователей Эпикура (300 г. до н. э.). Эта школа едва ли заслуживает упоминания в истории науки, так как ее основатель не проявлял никакого интереса к явлениям природы и фактически предоставлял всем совершенно свободно делать собственные выводы об их причинах. На вопрос, какого размера Солнца, он ответил: «Такого, каким видится»; а плоская Земля для него была осадком от падения атомов, которое, по его мнению, происходит по вертикали противоположно движению кругового вихря, о котором говорил Демокрит. Римский истолкователь учения Эпикура Лукреций Кар (живший в первой половине I в. до н. э.) необычайно отстает от своего времени, когда с презрением говорит об идее антиподов и оставляет открытым вопрос, продолжают ли Солнце и Луна свой путь под землей или ежедневно обновляются на востоке. С другой стороны, он предстает в выгодном свете, когда утверждает, что мир бесконечен и поэтому нельзя сказать, что Земля находится в его центре («О природе вещей», I, 1070). Если уж знаменитый философ считал Землю плоской, не приходится удивляться тому, что такой доверчивый писатель, как Ктесий, в начале IV века сообщал, что с некоторых гор в Индии Солнце кажется в десять раз больше, чем в Греции, или тому, что Посидоний снисходительно опровергал убеждение, распространенное среди жителей атлантического побережья, что Солнце садится в океан с шипением, или заявлению Артемидора Эфесского, что в Гадесе (то есть Кадисе, где он побывал самолично) Солнце, заходя, кажется в сто раз крупнее своего обычного размера (Страбон, III, с. 138). Не странно также и то, что поэт Лукан позволяет Атлантическому океану у западного побережья Ливии нагреваться от спускающегося в него Солнца, в то время как твердый небосвод удерживает облака, несомые восточными ветрами над Испанией. Даже Вергилий, описывая ход Солнца по зодиаку, не уверен, то ли в противоположном полушарии молчалива глубокая ночь и под ее покровом темнота не редеет густая, или же там Аврора встает и день постепенно приводит, а Веспер там зажигает вечерние светочи («Георгики», I, 247—251). Но хотя подобных народных суеверий и поэтических фантазий вряд ли достаточно для доказательства того, что доводы философов и естествоиспытателей еще не проникли в умы авторов ненаучной направленности и не стали достоянием народов в целом, у нас есть и другие данные, говорящие о том же. Мы уже видели, что Аристотель достаточно полно доказал шарообразную форму Земли; однако последующие авторы не считали излишним приводить как можно больше доказательств, хотя и пренебрегали одним весомым аргументом Аристотеля, а именно о неизменно округлой форме земной тени, падающей на Луну. Так, Посидоний (Клеомед, XIII, 8) показывает, что различные формы, предлагавшиеся ранними мыслителями, например плоская, подобная тарелке, кубическая или пирамидальная, несостоятельны по причине изменения видимого над горизонтом звездного неба по мере продвижения на север или юг, притом что персы видят восход Солнца на четыре часа раньше, чем иберийцы. Аргумент Аристотеля о том, что равноудаленность поверхности океана от центра Земли может существовать лишь при ее шарообразной форме, тоже регулярно появляется в ассортименте доводов любого писателя (Плиний, II, 165; Теон, с. 146).

Что касается размера шарообразной Земли, то Аристотель[146], одним из первых попытавшийся оценить его, указывает длину окружности в 400 000 стадиев, но не уточняет, на основании какого источника. У нас нет никаких сведений о том, что вавилоняне или египтяне когда-либо пытались определить размер Земли, и, значит, грубо приблизительные данные Аристотеля получены из какого-то греческого источника, не исключено, что из наблюдений Евдокса за разной высотой звезд, сделанных во время его пребывания в обеих странах. Следующую оценку приводит Архимед («Исчисление песчинок», I, 8), а именно 300 000 стадиев, тоже не ссылаясь на какой-либо авторитет, но, вероятно, он повторял данные единственного географа того времени – Дикеарха из Мессены, умершего около 285 г. до н. э., Страбон упоминает оцененные им расстояния в Средиземноморье. Труды Дикеарха утеряны, за исключением нескольких фрагментов, однако мы знаем, что он учил шарообразной форме Земли и заявлял, что высота Пелиона – 1250 шагов – несущественна по сравнению с размером Земли (Плиний, II, 162). Посидоний, вероятно, ссылается именно на эту оценку (Клеомед, I, 8), когда (доказывая, что Земля не плоская) говорит, что голова созвездия Дракона проходит через зенит во фракийской Лисимахии, в то время как в верхнеегипетской Сиене через зенит проходит Рак. Так как склонение этих звезд отличается на 24°, а расстояние между этими городами равно 20 000 стадиев, то, по его словам, диаметр мира равен всего лишь 100 000 стадиев, а окружность – всего 300 000 стадиев, из чего следует, что Земля не может быть плоской, так как это всего лишь точка в сравнении с небесной сферой, которая, по его расчетам, сама имеет весьма ограниченный размер. Очевидно, что размер Земли, если она шарообразная, должен в точности соответствовать этим расчетам. Лисимахия была основана в 309 году до н. э. Лисимахом, впоследствии царем Фракии; поэтому размер должен был вычисляться позже 309 года, но при этом раньше времени жизни Архимеда (который умер в 212 г.), так как у автора окружность равна трем диаметрам. Поэтому представляется весьма вероятным, что именно Дикеарху принадлежит эта оценка размера Земли, однако лишь весьма приблизительная, потому что Лисимахия находилась на широте около 40°33?, тогда как склонение у Дракона, самой яркой и самой южной звезды в голове Дракона, в 300 году до н. э. было равно +53°11?.

Следующую и самую знаменитую попытку определить размер Земли предпринял Эратосфен из Александрии (276– 194 до н. э.), библиотекарь великого Александрийского мусейона. Он был родом из Кирены и учился в Александрии и Афинах, так что он уже прославился как ученый к тому времени, когда его (около 235 года) призвали в Александрию, где он и провел остаток жизни. Он был человеком необычайно разнообразных талантов, но главным образом известен нам как географ, хотя и только по упоминаниям (часто враждебным) в сочинениях Страбона и других авторов. Видимо, в дополнение к своему великому труду по географии он написал особую книгу о вычислении размера Земли, впоследствии утраченную. Он утверждал, что в Сиене гномон не отбрасывает тень в день летнего солнцестояния, в то время как меридиональное зенитное расстояние Солнца в Александрии составляет ¹/₁₅₀, окружности небес, каковая дуга, таким образом, представляет разницу широты, в то время как линейное расстояние между этими местами – он исходил из того, что они находятся на одном меридиане, – составляет 5000 стадиев[147]. Следовательно, окружность Земли равна 250 000 стадиев, хотя позднее или сам Эратосфен, или кто-то из его преемников заменили это число на 252 000 стадиев[148], очевидно, для того, чтобы получить круглое число – 700 стадиев – для величины градуса. Это значение принимали Страбон и Плиний[149].

Итак, возникает вопрос: какова была длина стадия, принятая Эратосфеном? Ответ на этот вопрос дает Плиний, говоря, что у Эратосфена схен был равен 40 стадиям. Египетский ??????? (схен) равнялся 12 000 королевским локтям по 0,525 метра[150], то есть стадий был равен 300 таких локтей или 157,5 метра = 516,73 фута; значит, умноженное на 252 000, это дает нам 39 690 километров, или 24 662 мили, что соответствует диаметру 12 662 километра, всего на 80 километров меньше истинного полярного диаметра Земли. В значительной степени столь близкое соответствие, разумеется, обязано череде случайностей, хотя, с другой стороны, надо помнить, что мы лишь очень приблизительно представляем себе действия Эратосфена, и нам совершенно неизвестно, какие меры он принимал, чтобы исключить ошибки, особенно в наблюдении за зенитным расстоянием Солнца в Александрии. Клеомед добавляет, что наблюдения за тенью гномона в день зимнего солнцестояния в Сиене и Александрии дали тот же результат – ¹/₁₅₀, но не приводит никаких подробностей. Широта Сиены 24°5?[151], Александрийского мусейона – около 31°11,7? (Птолемей предполагает 30°58?), разница составляет 7°6,7?, что довольно близко к 7°12? Эратосфена. Но тропик Рака не проходил через Сиену во времена Эратосфена, так как наклон эклиптики около 225 года составлял 23°43?20?, в то время как Эратосфен нашел его равным 23°51?20?. До его времени он считался равным 24°[152], так что Эратосфен подошел ближе к истине.

Стадий, который использовал Эратосфен, был короче олимпийского, равного 185 метров (400 локтей по 0,462 метра), птолемеевского, или королевского, египетского стадия, равного 210 метров (400 локтей по 0,525 метра). Это была путевая мера длины для выражения расстояний, которая измерялась шагами, и всегда было известно, что она меньше олимпийского стадия. Согласно Марциану Капелле (VI, 598)[153], Эратосфен выяснил расстояние между Сиеной и Мероэ per mensores regios Ptolemaei, то есть с помощью профессиональных шагомеров, или бематистов – ?????????? (itinerum mensores), и потому естественно, что он использовал путевую меру длины, которую применяли и они. Ее же, по-видимому, использовал и Посидоний в следующей попытке определить размер Земли, которую также записал для нас Клеомед (I, 10). Посидоний, уроженец сирийской Апамеи, родился около 135 года до н. э.; он провел много лет в многочисленных путешествиях (вплоть до Испании), после чего поселился на Родосе и прославился как учитель стоической философии. Он был автором около двадцати работ, из которых до нас дошли только фрагменты. Он умер в возрасте 84 лет примерно в 50 году до н. э. Согласно Посидонию, яркая звезда Канопус на Родосе в момент кульминации находится прямо на горизонте[154], тогда как ее меридиональная высота в Александрии составляла «четверть знака, то есть одну сорок восьмую часть зодиака». Таким образом, разность широты составляет 7°30?, и при расстоянии 5000 стадиев[155] окружность Земли выходит равной 240 000 стадиев. Этот результат вызывает гораздо меньше доверия, чем результат Эратосфена. Конечно, невозможно увидеть звезду, когда она ровно на горизонте, но Темин («Элементы астрономии», III, с. 42) говорит нам, что на Родосе Канопус трудно увидеть или он виден только с возвышенностей, а Гиппарх просто говорит, что он виден с Родоса (комментарий к «Явлениям» Евдокса и Арата, XI, с. 114). В действительности истинная меридиональная высота Канопуса на Родосе в то время составляла около градуса, или, с учетом рефракции, 1°16?, чего достаточно, чтобы объяснить погрешность в 2°15? в разности широты, которая равна всего 5°15?[156]. Возможно, именно известная трудность четкого наблюдения края тени внушила Посидонию мысль, что желательно было бы проверить результат Эратосфена другим методом, не используя Солнца; но он вряд ли добивался того, чтобы его результат считали более предпочтительным. По всей видимости, он не был опытным наблюдателем, и на Родосе у него не было надлежащих инструментов, поэтому он счел удобным использовать звезду, высота которой близка к нулю. Возможно, он лишь использовал все это в качестве наглядной иллюстрации для урока и не претендовал на какую-либо ее научную ценность.

В своей «Географии» Птолемей указывает длину градуса – 500 стадиев и окружности – 180 000 стадиев. Так как это относится к значению Посидония точно так же, как путевой стадий к египетскому, очевидно, что Птолемей использовал официальный египетский стадий, равный 210 метрам, который практически равен ¹/₇ римской мили (всего лишь примерно на метр меньше) и, значит, был удобной единицей измерения для подданного Римской империи и жителя Египта. Он просто взял значение Посидония и перевел его в другую единицу измерения[157].

Таким образом, греческие астрономы имели довольно верное представление о размерах Земли. Теперь мы посмотрим, что они думали насчет расстояний между небесными светилами.

Первым философом, который стал рассуждать об этих расстояниях, был Анаксимандр. Он полагал, что расстояние до Солнца в 27, а до Луны – в 19 раз больше радиуса Земли, или, возможно, расстояние до Солнца в 27 раз больше расстояния до Луны[158]. Следующий мыслитель, кому приписывают размышления такого рода, – это Пифагор, и, как считается, его идеи по этому вопросу связаны с теорией «гармонии сфер». Единственное, что у нас есть на этот счет, мы знаем от авторов гораздо более позднего времени, но большинство философов после V века более-менее разделяли красивую фантазию о том, что всей Вселенной правит гармония, которая продолжала пленять человеческий разум до конца Средневековья:

Мы уже видели, что это была главная идея в платоновском учении о душе мира и что она привела его к заключению, что радиусы планетных орбит пропорциональны числам 1, 2, 3, 4, 8, 9, 27, хотя последнее из этих чисел не соответствует ни одной ноте в греческой музыке. Музыкальные звукоряды, приписываемые Пифагору разными авторами, не совсем совпадают. По Плинию («Естественная история», XXI, 84), интервалы между планетами таковы:

Земля – Луна: тон.

Луна – Меркурий: полутон (dimidium ejus spati).

Меркурий – Венера: полутон (fere tantundem).

Венера – Солнце: малая терция (sescuplum).

Солнце – Марс: тон.

Марс – Юпитер: полутон (dimidium).

Юпитер – Сатурн: полутон (dimidium).

Сатурн – неподвижные звезды: малая терция (sescuplum).

Звукоряд соответствует нотам до, ре, ми-бемоль, ми, соль, ля, си-бемоль, си, ре. Плиний допускает прискорбную оплошность, прибавляя, что «всего получается семь тонов, что образует «октаву», именуемую у греков «гармонией», в то время как он состоит из двух частей, каждая из которых образует квинту. Но так как Земля покоится в неподвижности, она не может издавать звуки, и, если вывести ее из рассуждения, интервалы от Луны до неподвижных звезд действительно образуют октаву дорийского лада. У Цензорина последний интервал – полутон (limma), но в остальном он полностью согласен с Плинием[160]. Тогда неподвижные звезды соответствуют не ре, а до и весь ряд образует октаву (диапазон), но она не совпадает с музыкальной системой Пифагора, в которой интервал от средней до самой высокой ноты составляет всего лишь квинту. Цензорин также забывает, что вначале он заявил, что только семь планет издают музыку. Тот же самый звукоряд указывает и Теон (с. 187), ссылаясь на поэта Александра[161], и очень похожую – Ахилл, то есть до, ре, ми, фа, соль, ля, си-бемоль, си, до, с интервалами 1, 1, ?, 1, 1, ?, ?, ? и Солнцем, идущим после Луны. Однако очень важно отметить то обстоятельство, что все эти звукоряды встречаются только у очень поздних авторов. Из ссылок у Платона и Аристотеля мы знаем, что общая идея гармонии сфер уходит еще к началу IV века до н. э. Конечно, она могла возникнуть и раньше, хотя в таком случае Филолай должен был ее проигнорировать, так как она несовместима с его системой из десяти планет. Следующая ссылка содержится в так называемом Папирусе Евдокса, где утверждается, что Солнце гораздо больше Луны (и вследствие этого, поскольку их угловые диаметры равны, Солнце находится гораздо дальше, чем Луна), так как диапента (квинта) больше диатессарона (кварты), иначе говоря, расстояние до Солнца так же относится к расстоянию до Луны, как квинта к тону или как 9 к 1[162]. Это та же пропорция, которую приводят Плиний и другие поздние авторы, но в остальном у них совершенно иная точка зрения на вопрос, потому что расстояния у них пропорциональны интервалам, а не представляющим их числам, то есть расстояние до Солнца становится в З? раза больше расстояния до Луны, а не в 9 раз, как у Евдокса. Также вводится более поздний порядок расположения планет[163], и вся система превращается в кучу произвольных допущений, так что даже идея о том, что неподвижные звезды издают самую высокую ноту (????), а Луна – самую низкую (?????), перевернута наоборот у неопифаторейца Никомаха. Его мысль, очевидно, состоит в том, что Луна, как ближайшее к Земле тело, должна соответствовать самой короткой, а Сатурн – самой длинной струне из семи струн лиры. Другие теоретики в соответствии с пятью тетрахордами так называемой совершенной системы предполагали в небесах пять равных интервалов, один от Луны до Солнца (с Меркурием и Венерой), второй оттуда до Марса, третий от Марса до Юпитера, четвертый от Юпитера до Сатурна, пятый от Сатурна до сферы неподвижных звезд. И в то время как одни вслепую нащупывали гармонию Вселенной в расстояниях между планетами, другие искали ее в сухости, тепле, влажности или твердости звезд; или вместе с Птолемеем сравнивали угловые расстояния планет в небе с музыкальными интервалами, так чтобы октава соответствовала 180° (противостояние), а квинта – 120° (тритон), кварта – 90° (квадратура), секунда – 60° (aspectus sextilis). На самом же деле едва ли нужно относиться серьезно к планетным интервалам, определяемым гармонией сфер; вся эта теория очень похожа на астрологию, хотя и гораздо более возвышенна по своему замыслу и заслуживает уважительного упоминания в истории человеческого прогресса.

Плиний и Цензорин начинают рассуждения об этих звукорядах с того, что Пифагор полагал, будто расстояние до Луны составляет 126 000 стадиев, и Плиний прибавляет, что расстояние от Луны до Солнца вдвое больше, а расстояние от Солнца до неподвижных звезд – втрое, «какого мнения был и наш соотечественник Галл Сульпиций». Эти сведения, которые в деталях не согласуются с его музыкальным звукорядом, Плиний, очевидно, взял из другого источника: или из книги Гая Сульпиция Галла о затмениях, или из энциклопедии Теренция Варрона, обе эти работы он упоминает среди своих источников во второй книге своей естественной истории. Расстояние до Луны 126 000 стадиев составляет ровно половину значения, которое указывает Эратосфен для окружности Земли, и это явный знак того, что Пифагор не мог иметь к этой оценке никакого отношения. Хотя удивительно малое расстояние до Луны (всего в 1? раза больше диаметра Земли) выглядит архаически, скорее всего, это всего лишь продукт невежества какого-то более позднего автора, который не знал об исследованиях ученых или не придавал им важности, если только какая-то ошибка не вкралась в цифры в копии одной из книг, которыми пользовался Плиний. Столь же сумасбродные оценки приводит и Марциан Капелла (VIII, 856—861). Отношение расстояний попросту должно быть таким же, как отношение периодов, то есть расстояние до Луны равно ¹/₁₂ расстояния до Солнца, а Марс, Юпитер и Сатурн соответственно в 2, 12 и 28 раз дальше Солнца. Автор, по-видимому, взял свои данные у Варрона, и его восьмая книга, таким образом, всего лишь отражает состояние знаний в Риме в I веке до н. э. Расстояние до Луны, по его мнению, равно 100 земным радиусам, что якобы следует из видимого диаметра Луны 36?, найденного исходя из того времени, которое требуется Луне, чтобы пересечь горизонт, и диаметра лунной тени во время полного солнечного затмения, который, по его словам, равен ¹/₁₈ окружности Земли, как показали наблюдения от Борисфена до Мероэ. Очевидно, что он переписывал данные из источников, которые не совсем понимал, и его информация о размерах Земли столь же ошибочна, так как он указывает окружность, равную 406 010 стадиев, ссылаясь на авторитет Эратосфена и Архимеда.

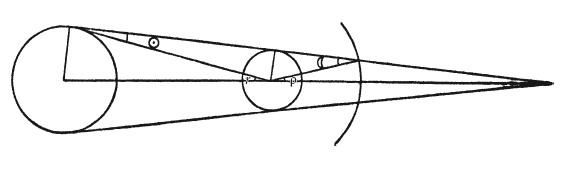
Вернемся же теперь к не вызывающим сомнения результатам серьезного труда по этому вопросу, который затрагивает только Солнце и Луну. От Аристотеля («Метеорологика», I, 8, с. 345 b) мы узнаем, что уже в его дни проблема размера и удаленности Солнца и Луны уже начала привлекать внимание. «Суда» (в главе «Философы») приписывает его современнику Филиппу Опунтскому авторство книг о расстоянии до Солнца и Луны, о размерах Солнца, Луны и Земли, о лунных затмениях и планетах. Евдокс, как мы уже видели, считал, что диаметр Солнца в 9 раз больше диаметра Луны и, следовательно, расстояние до Солнца в 9 раз больше расстояния до Луны, так как видимый размер обоих светил кажется одинаковым. Архимед, упоминая это, прибавляет, что его отец[164] Фидий вычислил это отношение как 12:1. Сам Архимед исходил из отношения 30:1. Откуда взялись эти цифры, нам уже никак не узнать, однако есть вероятность, что методы, которыми пользовался Аристарх в следующем веке, на самом деле выработаны Евдоксом. Мы уже говорили, что Аристарх попытался определить относительные расстояния до Солнца и Луны и нашел, что первое примерно в 18—20 раз больше второго. В книге «О размерах и расстояниях Солнца и Луны» он также указывает, каким методом определил расстояние до Солнца, который, по Птолемею, применял и Гиппарх и которым астрономы пользовались еще шестнадцать веков. Он основан на наблюдениях за шириной земной тени на среднем расстоянии, на котором Луна пересекает ее во время лунных затмений. На рисунке ? составляет половину этой угловой ширины, найденной измерением времени, которое требуется Луне, чтобы пересечь тень, тогда как г — угловой радиус Солнца, а ? и ? – параллаксы Солнца и Луны. Очевидно, что

По Гиппарху, г = 16?36?55?? и ? в 2?, раза больше («Синтаксис», IV, 8), и, если мы вместе с Аристархом примем ? = 19 ?, это дает ? = 2?54?.

Но Гиппарх не удовольствовался этим методом нахождения суммы параллаксов Солнца и Луны, который может служить лишь для нахождения лунного параллакса; напротив, он, видимо, знал, что солнечный параллакс он таким методом выяснить не сможет в силу ошибок наблюдения, которых невозможно избежать. Из слов Птолемея (V, 11) представляется, что Гиппарх попытался найти пределы, в которых может лежать солнечный параллакс, чтобы согласовать наблюдения и расчеты в случае солнечного затмения, когда может проявиться разница параллаксов Солнца и Луны, тогда как сумму параллаксов можно было найти с помощью лунных затмений. Естественно, этот метод не дал никаких результатов, так что Гиппарх не был даже уверен, можно ли вообще определить солнечный параллакс или можно ли принять его равным 0. Во втором случае вышеприведенные значения для г и ? дают ? = 58?9?14??, что соответствует расстоянию до Луны, равному 59,1 полудиаметра Земли, и в 3? раза больше полудиаметра Луны. Птолемей не говорит, какой верхний предел нашел Гиппарх, но, вероятно, Клеомед имел его в виду, сказав (II, 1), что Гиппарх доказал, что Солнце в 1050 раз больше Земли. Поскольку здесь речь идет об объеме, полудиаметр Солнца оказывается в ¹⁰/₆ раза больше полудиаметра Земли, а полудиаметр Луны – в 1 : 3²/₅ раза (эти данные принимал Птолемей), и расстояния до Луны и Солнца соответственно равны 60⁵/₆ и 2103 земным радиусам. Теон приводит среднее между этими предельными значениями, утверждая, что Гиппарх полагал, что Солнце в 1880 раз больше Земли, то есть его радиус в 12? раза больше, расстояние равно 2550 земным радиусам, радиус Луны равен ¹²/₄₁ = 0,29, а ее расстояние – 60,5 земного радиуса.

Так как расстояние до Луны в 60? раза больше экваториального радиуса Земли, а ее полудиаметр равен 1:3? или 0,273 полудиаметра Земли, мы видим, что Гиппарх имел очень верное представление о размере и удаленности нашей ближайшей небесной соседки[165]. Проблема нахождения расстояния до

Солнца (и, следовательно, его истинного размера) находилась вне досягаемости инструментальных возможностей астрономов до изобретения телескопа, однако это делает большую честь Гиппарху, что, приступив к проблеме с разных сторон, он понял, что ее придется оставить неразрешенной. С другой стороны, Птолемей, определив лунный параллакс путем сравнения зенитных расстояний с теми, которые вытекали из его теории, сделал явный шаг назад, когда вывел расстояние до Солнца из лунных затмений, что практически идентично результату, следующему из найденной Аристархом пропорции; и в течение полутора тысяч лет астрономы без лишних вопросов принимали его солнечный параллакс, равный 2?51?. Он использовал следующие данные («Синтаксис», Y, 15—16, с. 425—426):

1210[166]

5,5 [167]

Интересно, однако, отметить, что Гиппарх не единственный астроном своей эпохи, осознавший, что Солнце не в 20 раз, а намного, гораздо дальше Луны. Достойную упоминания попытку определить фактический размер Солнца, основанную на смелой гипотезе относительно его расстояния, предпринял Посидоний, о чем сообщают нам Клеомед (II, 1) и Плиний (II, 85). Посидоний, опираясь на Эратосфена, знал, что в Сиене, под тропиком Рака, в области диаметром 300 стадиев в момент, когда Солнце находится в созвездии Рака, в полдень не видно теней. То есть на любую точку в пределах этой области падают прямые лучи Солнца в направлении перпендикулярном поверхности Земли, и, так как любой перпендикуляр к поверхности сферы проходит через ее центр, Посидоний заключил, что конус с вершиной в центре Земли и основанием в видимом диске Солнца отсекает от поверхности

Земли круг диаметром 300 стадиев. Если допустить, что орбита Солнца в 10 000 раз больше окружности Земли, то диаметр Солнца в 10 000 раз больше диаметра площади, в которой предметы не отбрасывают тени. Если теперь мы спросим, какой радиус Земли предположил Посидоний, ответ мы найдем в следующих цифрах у Плиния, который, вероятно, взял их из своего обычного источника – Теренция Варрона. Согласно Плинию, Посидоний предположил, что расстояние от поверхности Земли до области облаков и ветров составляет 40 стадиев, оттуда (inde) начинается ясный и прозрачный воздух, полный безмятежного света, но между облачной областью и Луной находится пространство в 2 000 000 стадиев, а оттуда (inde) до Солнца – 500 000 000 стадиев, «и только благодаря такому расстоянию Солнце при своем громадном размере не сжигает Землю». Если соединить это с утверждением Клеомеда, что диаметр Солнца равен 10 000 ? 300 стадиев, то простой подсчет дает радиус Земли 50 205,02 стадия. Но текст у Плиния явно подвергся искажению, так как нет никакого смысла в предположении, что расстояние от поверхности Земли до Солнца равно 502 000 040 стадиев, ведь использовались только круглые числа. Нет никаких сомнений, что второе inde следует вычеркнуть и Посидоний просто высчитал расстояние до Солнца от центра Земли, равное 500 000 000 стадиев, и радиус Земли, равный одной десятитысячной части расстояния, то есть 50 000 стадиев. Таким образом, в округленных числах окружность составит 300 000 стадиев, или ровно в 1000 раз больше области без тени. Тот факт, что Посидоний не принял величину окружности Земли 240 000 стадиев, которую вычислил сам, а использовал гораздо более старую величину 300 000 стадиев, нужно считать еще одним доказательством того, что он хотел оперировать только круглыми числами. Аналогичным образом, видимый диаметр Солнца стал 360° : 1000, хотя он и знал, что 360°: 720 намного ближе к истине. По сути дела, он следовал по пятам за Архимедом, который в своем «Исчислении песчинок» стремился мысленно образовать самую большую сферу, какую только можно себе представить, наполнить ее песчинками, пересчитать их и затем доказать, что всегда можно представить себе число еще больше. С этой целью Архимед произвольно предположил, что длина окружности Земли равна 3 000 000 стадиев, а длина окружности орбиты Солнца в 10 000 раз больше. Посидоний взял у него второе число, показав тем самым, что не верит в большой параллакс и, следовательно, малое расстояние до Солнца, хотя этого мнения придерживались все астрономы Античности, за исключением Гиппарха.

Так как гипотеза Посидония не имела под собой никаких оснований в наблюдаемых фактах, Птолемей ее не упоминает; также игнорирует он и чрезвычайно беспечное заявление Клеомеда (II, 1), что раз уж (согласно Аристарху, которого он не упоминает) тень Земли на расстоянии Луны вдвое больше лунного диаметра, то лунный диаметр должен был равен половине земного, или 40 000 стадиев. Так он получает расстояние до Луны, равное 5 000 000 стадиев (в два с лишним раза больше фактического расстояния), и исходя из того, что фактические скорости планет на их соответствующих орбитах одинаковы, расстояние до Солнца в тринадцать раз больше. Неудивительно, что Птолемей не стал тратить времени на опровержение подобных заявлений.

Ради полноты картины коротко скажем, что Макробий в V веке н. э. делает любопытное утверждение относительно размера Солнца («Сон Сципиона», I, 20). Без малейшей попытки доказать это он объявляет, что тень Земли достигает орбиты Солнца и равна шестидесяти земным диаметрам. Из этого допущения следует, исходя из того, что длина тени равна радиусу орбиты Солнца, что диаметр Солнца в два раза больше диаметра Земли[168]. Макробий просто указывает в качестве авторитета некоего «египтянина», и вся его история достаточно груба, чтобы происходить из доалександрийского источника, хотя, скорее, он просто переписал ее у какого-то невежественного энциклопедиста, который не дал себе труда вникнуть в скорый прогресс научной астрономии.

Итак, мы увидели, что крайне несовершенные идеи ранних философов в отношении протяженности известной нам части Вселенной постепенно уступили место более правильным представлениям о размере Земли и размере и удаленности Луны. В то же время астрономы александрийской школы и их современники довольно четко осознавали тот факт, что другие планеты системы находятся на значительно большем расстоянии от нас, хотя их идеи об этих расстояниях оставались далекими от реальности. Цицерон называет расстояния, отделяющие орбиты трех внешних планет друг от друга и от звездного неба, «бесконечными и огромными» и добавляет, что сами небеса являются крайним пределом мира («О дивинации», II, 43, 91). Сенека в главе о природе комет («Естественно-научные вопросы», VII, 12) указывает на то, что планеты разделены большими интервалами даже в то время, когда две из них представляются находящимися близко друг от друга, и по этой причине мнение, что кометы образуются при сближении планет, не имеет под собой никаких оснований. Что же касается неподвижных звезд, то идея, что они расположены на поверхности сферы огромного, хотя и ограниченного размера, продолжала оставаться общепризнанной практически повсеместно[169].

Система эпициклов, в последний раз усовершенствованная Клавдием Птолемеем во II веке, оказалась не в состоянии дать ключа к межпланетным расстояниям. Она смогла только вычислить для каждой планеты соотношение между радиусами деферента и эпицикла, вытекавшее из наблюдаемой длины ретроградной дуги. Но более поздние авторы не желали и дальше пребывать в невежестве в вопросе размера планетных орбит. Предполагалось, что расстояния до Луны и Солнца известны, и, так как в пространстве между ними находились орбиты Меркурия и Венеры, «некоторые люди» (?????), как говорит нам Прокл, предположили, что в мире нет пустого пространства и что все интервалы заполнены промежуточными сферами. Наибольшее расстояние до Луны составляет 64¹/₆, и это также наименьшее расстояние до Меркурия, в то время как наибольшее расстояние до Меркурия, вычисленное по отношению Птолемея, составляет 177 ³³/₆₀ и равно наименьшему расстоянию до Венеры, наибольшее расстояние до которой, вычисленное аналогичным образом, составляет 1150, что почти равно 1160, перигейному расстоянию Солнца («Обзор астрономических гипотез»). Спустя столетие мы видим, что Симпликий утверждает тот же принцип (не приводя никаких цифр) и невозмутимо приводит в качестве своего авторитета «Синтаксис» Птолемея, в котором об этом нет ни слова («О небе»). Однако на протяжении всего Средневековья эта идея была общепринятой, и ниже мы увидим, что вплоть до времен Коперника размеры всех планетных орбит, рассчитанные на основе этого принципа, считались хорошо известными.

В то время как знания о размерах Вселенной постепенно совершенствовались, мыслителям оказалось куда труднее прийти к согласию относительно физического устройства небесных тел, хотя все признавали их огненную природу. Стоики, в частности, полагали, что они состоят из чрезвычайно чистого огня или эфира, который пронизывает все верхние области пространства. Естественно, своеобразная наружность «лика Луны» указывала на то, что она имеет совершенно иной состав, и уже Анаксагор и Демокрит признавали, что это масса твердого вещества с горами и равнинами, а Платон полагал, что она в основном состоит из материи, подобной земной. Все, что самые просвещенные умы Античности смогли выяснить в вопросе состава Луны, содержится в замечательнейшем диалоге Плутарха «О лике, видимом на диске Луны». В этой книге опровергается мнение стоиков о том, что Луна представляет собой смесь воздуха и огня, так как Луна не была бы невидима во время новолуния, если бы не заимствовала весь свой свет от Солнца; это также доказывает, что она состоит не из вещества вроде стекла или кристалла, поскольку тогда невозможны были бы солнечные затмения. То, как солнечный свет отражается от Луны, и отсутствие яркого отраженного образа Солнца и Земли доказывает, что вещество Луны не гладкое и блестящее, а подобно веществу нашей Земли. Далее следует правильное объяснение того, что Луна остается едва видимой во время лунных затмений. Весьма любопытно, что Плутарх с целью опровергнуть идею о том, что Луна не может быть такой же, как Земля, поскольку не находится ниже всего, смело утверждает, что нахождение Земли в центре Вселенной не доказано, так как пространство бесконечно и потому не имеет центра; к тому же, если все землеобразное и тяжелое скапливается в одном месте, следует ожидать, что и все огненные светила должны соединяться вместе в единое тело. И все-таки Солнце отстоит от верхней сферы на бесчисленные миллионы стадиев, тогда как другие планеты не просто ниже неподвижных звезд, но несутся по орбитам на громадных расстояниях друг от друга; а Луна настолько ниже звезд, что расстояние от нее до них невозможно вычислить, притом что она находится очень близко к Земле, на которую чрезвычайно похожа по устройству.

В то время как Плутарх совершенно очевидно осознавал истинную природу Луны, Сенека в седьмой книге своих «Естественно-научных вопросов» столь же разумно рассуждает о другом виде небесных тел – кометах. Он указывает (VIII, 30), насколько мнение стоика Панеция о том, что кометы – не полноправные светила, а лишь их ложные призраки, противоречит наблюдаемым фактам. Сенека говорит, что они не могут быть просто атмосферными явлениями, так как не зависят от ветра или гроз, но их движение идеально упорядочено. Он отбрасывает довод против их принадлежности к небесным светилам, заключающийся в том, что они не ограничиваются зодиаком, а блуждают по всему небу, и (вместе с Артемидором Парийским) говорит, что у нас нет никаких оснований полагать, будто существуют лишь те немногие планеты, которые мы знаем (и которые движутся по зодиаку), ведь могут быть и другие, обычно невидимые, потому что орбиты их расположены так, что они становятся видны лишь в какой-либо крайней их точке (VII, 13). Аналогичного мнения придерживался и Аполлоний из Минда[170], считая их отдельным видом небесных светил, которые обычно проходят через верхние области пространства и являются нам только в нижней части своих орбит (VII, 17).