Книга: Мир математики. т.30. Музыка сфер. Астрономия и математика

Глава 3. Как определить массу центральной звезды планетной системы

Глава 3. Как определить массу центральной звезды планетной системы

Рассмотрим движение экзопланет вокруг центральной звезды по круговой орбите радиуса а. Приравняем силы, действующие на планету:

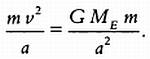
Упростив, получим значение скорости v:

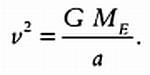
Период Р обращения планеты вокруг звезды по круговой орбите равен:

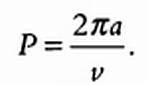
Подставив в это выражение приведенное выше значение скорости v, имеем:

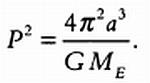
Для каждой экзопланеты можно выразить постоянную, которая приводится в третьем законе Кеплера:

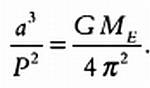
Записав указанное выше соотношение для Земли, период обращения которой вокруг Солнца равен Р = 1 год, а радиус орбиты, которую мы будем считать окружностью, равен а = 1 а. е., получим следующее уравнение:

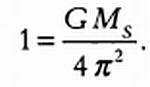
Разделив друг на друга два последних равенства и приняв массу Солнца M_s  = 1, получим:

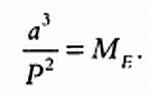
Мы знаем, что а — радиус орбиты (в а. е.), Р — период обращения (в годах), таким образом, мы можем определить массу центральной звезды М_E (точнее, отношение ее массы и массы Солнца). Масса центральной звезды в планетной системе М_E (относительно массы Солнца) рассчитывается по формуле:

где а — радиус орбиты экзопланеты (в км), Р — период обращения вокруг звезды (в днях). По этой формуле можно вычислить массу звезд Ипсилон Андромеды и Глизе 581 относительно массы Солнца. Полученные значения будут соответствовать приведенным в таблице на странице 60.