Книга: Мир математики. т.30. Музыка сфер. Астрономия и математика

Глава 2. Вычисления расстояний в системе «Земля — Луна — Солнце», выполненные Аристархом Самосским

Глава 2. Вычисления расстояний в системе «Земля — Луна — Солнце», выполненные Аристархом Самосским

Аристарх Самосский (310 год до и. э. — 230 год до н. э.) определил отношения между расстояниями и радиусами небесных тел в системе «Земля — Луна — Солнце». Он вычислил отношение между радиусом Солнца и радиусом Луны, между расстоянием от Земли до Солнца и расстоянием от Земли до Луны, а также определил отношение радиуса Земли ко всем этим расстояниям. К сожалению, исследователь не смог рассчитать значение радиуса нашей планеты и вычислить абсолютные значения всех остальных радиусов и расстояний. Радиус Земли определил Эратосфен несколько лет спустя. Применив современную нотацию (и современные значения), мы покажем, как действовал Аристарх Самосский, и предложим читателю повторить его эксперимент. Вы убедитесь, что, проведя необходимые наблюдения, нетрудно получить те же результаты, что и древний мыслитель.

Отношение расстояний между Землей и Луной и Землей и Солнцем Аристарх Самосский определил, что угол, под которым с Земли виден отрезок, соединяющий Солнце и Луну, когда Луна находится в первой четверти, равен 87°.

Сегодня мы знаем, что он допустил ошибку — возможно, потому, что определить точный момент, когда Луна находится в первой четверти, очень сложно. Реальное значение этого угла равно 89°51’, в остальном же метод Аристарха Самосского полностью корректен. Обозначим через TS расстояние от Земли до Солнца, через TL — расстояние от Земли до Луны. Так как sin (9’) = TL/TS, имеем:

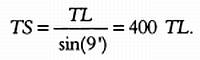
Аристарх Самосский вычислил, что TS = 19 TL.

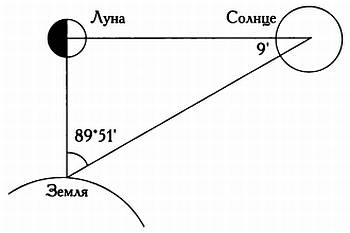
Расположение Луны в первой четверти относительно Земли и Солнца.

Отношение между радиусом Луны и Солнца

Отношение между радиусом Луны и Солнца должно рассчитываться по формуле, похожей на указанную выше, так как при наблюдении с Земли диаметры Луны и Солнца равны 0,5°. Следовательно, выполняется соотношение:

R_s = 400R_l.

Отношение между расстоянием от Земли до Луны и радиусом Луны или между расстоянием от Земли до Солнца и радиусом Солнца

Так как диаметр Луны при наблюдении с Земли равен 0,5°, отложив его 720 раз, можно полностью покрыть орбиту Луны (предполагается, что она имеет форму окружности). Длина ее орбиты в 2? раз больше расстояния от Земли до Луны, то есть 2R_L ? 720 = 2?TL. Выразив из этой формулы TL, имеем:

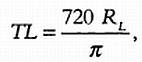
Проведя аналогичные рассуждения и предположив, что Земля вращается вокруг Солнца по окружности радиуса TS,

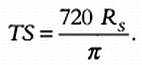
Отношение между расстояниями до Земли и радиусами Луны, Солнца и Земли

Во время лунного затмения Аристарх Самосский заметил, что Луна находится в конусообразной тени Земли в два раза дольше, чем необходимо, чтобы поверхность Луны была полностью покрыта тенью. Он сделал вывод: диаметр конусообразной тени Земли в два раза больше диаметра Луны, таким образом, отношение между этими диаметрами (а следовательно, и радиусами) равно 2:1. Сегодня известно, что отношение радиуса Земли к радиусу Луны равно 2,6:1. Во время лунного затмения с помощью хронометра можно определить отношения интервала между первым и последним соприкосновением границы Луны с конусообразной тенью Земли (этот интервал укажет диаметр конусообразной тени Земли) и интервала, в течение которого поверхность Луны окажется полностью покрыта тенью. Проведя расчеты, нетрудно получить значение, близкое к 2,6:1.

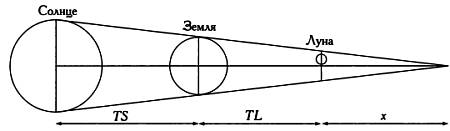
Конусообразная тень Земли и относительное расположение Земли, Луны и Солнца.

Используя обозначения, указанные на иллюстрации, установим следующие соотношения (х — вспомогательная переменная, которая используется для упрощения расчетов):

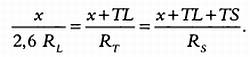
Подставив в эту систему уравнений соотношения Ts = 400T_L и Rs= 400R_L, исключим вспомогательную переменную х. Упростив выражения, получим:

Эта формула позволяет выразить все приведенные выше расстояния через радиус Земли:

Сюда нужно подставить радиус нашей планеты, чтобы определить все расстояния и радиусы небесных тел в системе «Земля — Луна — Солнце». Аристарху Самосскому не удалось вычислить радиус Земли, следовательно, он получил лишь ряд соотношений, но не расстояния и радиусы в явном виде. Сегодня радиус Земли до экватора известен: он равен 6645 км. Подставив это значение в приведенные выше выражения, получим следующие результаты: R_L = 1850 км (реальное значение 1738 км), расстояние TL = 424000 км (реальное значение — 384000 км), Rs = 740000 км (реальное значение — 696000 км), расстояние TS = 169600000 км (реальное значение — 149680000 км).

Мы привели эти результаты не для того, чтобы сравнить их с фактическими значениями, а для того чтобы показать, насколько умело действовал грек, получивший настолько точные значения примитивными методами.

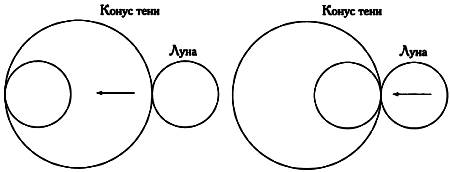
Зная точный момент первого и последнего касания границы Луны и конусообразной тени, можно определить диаметр сечения конуса (слева). Зная время, за которое тень покроет поверхность Луны, можно измерить диаметр Луны (справа).