Книга: Мир математики. т.30. Музыка сфер. Астрономия и математика

Глава 1. Преобразование координат и треугольник «полюс-зенит-звезда»

Глава 1. Преобразование координат и треугольник «полюс-зенит-звезда»

Преобразование азимутальных и экваториальных координат производится по правилам сферической тригонометрии. В современной математике эти преобразования координат описываются матрицами преобразований.

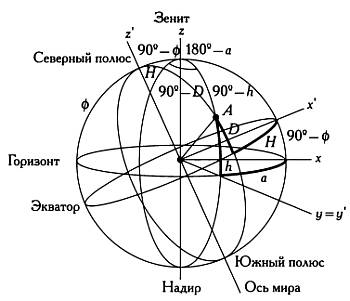
На иллюстрации положение звезды А определяется вектором, три составляющие которого определяются проекциями звезды на плоскость горизонта (плоскость ху) и ось зенит — надир (ось z). Таким образом, положение звезды задается тремя координатами: х, у, z. Следовательно, в горизонтальных координатах положение звезды А можно определить как вектор (r ? cos(h) ? cos(a), r ? cos(h) ? sin(a), r ? sin(h)).

Аналогично определяется положение звезды относительно небесного экватора (плоскости х’у’) и оси мира (оси z’), то есть осей экваториальных координат х’ у’ z’: (r ? cos(D) cos(H), r ? cos(D) ? sin(H), r ? sin(D)). Как показано на предыдущем рисунке, мы можем перейти от координат х, у, z к координатам х’ у’ z’ всего лишь выполнив поворот относительно оси у у которая совпадает с осью у’ на угол (90° — ф), где ф — широта. В результате х перейдет в ось х’ ось z — в ось z. Матрица преобразований относительно второй оси (оси у = у’) для угла (90° — ф) записывается так:

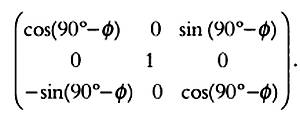
Имеем:

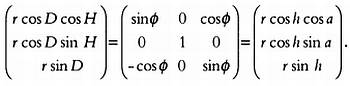
Следовательно, формулы преобразования координат записываются так:

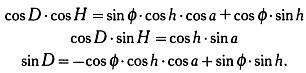
Те же соотношения, что выводятся с помощью матрицы преобразований, можно получить по формулам сферической тригонометрии Бесселя, рассмотрев треугольник «полюс-зенит-звезда», изображенный на иллюстрации на следующей странице.

На протяжении многих лет астрономы использовали этот треугольник для вычисления положения звезд. Так как ранее в их распоряжении не было ни компьютеров, ни других вычислительных машин, инструментами служили логарифмы и логарифмические таблицы. В этих таблицах приводились значения логарифмов для тригонометрических функций, аргументы которых выражались в градусах, минутах и секундах. Сферический треугольник «полюс-зенит-звезда» по-прежнему широко используется в сферической, или позиционной, астрономии, так как он содержит всю информацию, представленную на иллюстрации на предыдущей странице. Следует учитывать, что сторонами этого треугольника являются дуги большого круга небесной сферы. Следовательно, их длина измеряется в градусах, однако, по традиции, часовой угол и прямое восхождение отсчитываются в часах, минутах и секундах. Перейти от часов к градусам очень просто — достаточно учесть, что 360° эквивалентны 24 часам, или, что аналогично, 15° эквивалентны 1 часу.

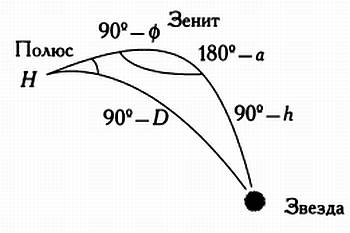
Треугольник полюс — зенит — звезда.