Книга: Ритм Вселенной. Как из хаоса возникает порядок

Глава 6. Мосты

Глава 6. Мосты

Это было время скрытых параллелей, время жизни в неосязаемом синхронизме. На календаре – 1962 г. Брайан Джозефсон начинал учебу в аспирантуре. Артур Уинфри поступал в колледж. Мишель Сиффре дрожал от холода в пещере глубоко под землей, подвергая свой организм малоизученному влиянию «жизни вне времени». Норберт Винер разъезжал по коридорам МТИ на своем уницикле, подкрепляясь арахисом, покуривая свою неизменную сигару и пытаясь отыскать аудиторию, в которой ему предстояло прочитать свою очередную лекцию[157]. Вот уже несколько месяцев Лев Ландау лежал в одной из московских больниц, отчаянно цепляясь за жизнь после ужасной автокатастрофы. Все они либо уже сделали, либо собирались сделать серьезный вклад в науку о синхронизме. Тем не менее они работали независимо друг от друга. Лишь десятилетия спустя мы начали осознавать истинную глубину связей между ними, а также между ними и Кристианом Гюйгенсом, который ровно за триста лет до описываемого нами времени, постоянно находясь у себя дома на протяжении нескольких дней, наблюдал синхронные колебания маятников своих настольных часов. Сейчас мы рассматриваем работу этих ученых как часть некого сложного целого. Мостом, который связывал воедино отдельные составляющие этого целого, служила математика.

Первый из замеченных учеными «математических мостов» соединял хорошо знакомый мир нашего повседневного опыта со странным миром квантов[158]. В 1968 г. Д. Е. Маккамбер из Bell Laboratories и У. С. Стюарт из RCA Laboratories, независимо друг от друга, изыскали способы, с помощью которых можно анализировать электрические характеристики перехода Джозефсона, как если бы он был обычным элементом электрической цепи. Точно так же как резистор подчиняется закону Ома (ток через резистор пропорционален напряжению на нем), переход Джозефсона подчиняется собственному закону, определяющему связь между током и напряжением. Этот закон формулируется так: когда ток, поступающий от внешнего источника, проходит через переход Джозефсона, он разделяется и движется по трем отдельным каналам, каждый из которых характеризуется собственным механизмом проводимости. Часть этого тока переносится куперовскими парами электронов и представляет собой упоминавшийся мною в предыдущей главе сверхток, который, проходя сквозь изолирующий барьер, не встречает на своем пути никакого сопротивления; остальные части тока переносятся обычными, не спаренными электронами и так называемым «током смещения» (форма проводимости, связанная с измененяющимся напряжением на переходе).

Принимая во внимание все три пути прохождения тока, Маккамбер и Стюарт выяснили, что динамические характеристики перехода Джозефсона наиболее естественным путем выражаются через изменение его фазы, меру того, насколько рассинхронизированными оказываются квантовые волны при переходе с одной стороны барьера на другую. Уже в этом заключалась новизна: в обычных законах электричества нет даже малейших следов чего-нибудь такого, что носит на себе отпечаток квантовой механики. Присмотревшись повнимательнее, Маккамбер и Стюарт заметили, что уравнение для электрических осцилляций представляло собой слегка замаскировавшегося старого знакомого: уравнение, известное любому студенту-первокурснику.

Это было уравнение, описывающее колебания маятника.

Это совпадение было из тех, которые вызывают у математика благоговейный трепет. «Ты испытываешь удивительное чувство, – говорил Эйнштейн, – когда выявляешь единство целого комплекса явлений, которые при непосредственном рассмотрении кажутся совершенно не связанными между собой». На первый взгляд, маятники Гюйгенса и переходы Джозефсона кажутся полными противоположностями. Маятники привычны и понятны каждому из нас, у них, если можно так выразиться, «человеческие» размеры; маятник знаком нам так же хорошо, как детские качели или как дедушкины настенные часы. Сверхпроводящие переходы Джозефсона так же непонятны большинству из нас, как пришельцы из иных миров. Нам непривычно в них буквально все: их размеры, сопоставимые с размерами какой-нибудь бактерии, непостижимая частота электрических колебаний в этих переходах (в 100 миллиардов раз выше частоты сердцебиения), сверхъестественное проникновение электронов сквозь непроницаемые барьеры, подобно привидениям, свободно проходящим сквозь стены. Между тем указанные различия не играют принципиальной роли. Главное же заключается в схожести динамических характеристик переходов Джозефсона и маятников. Картины их поведения во времени идентичны: две вариации на одну и ту же алгебраическую тему.

Узнав старого приятеля мы, к огромному своему сожалению, вынуждены констатировать, что в этом случае нам снова придется столкнуться с неизбежной трудностью: уравнения, описывающие колебания маятника, являются нелинейными уравнениями[159].

В частности, изгибающий момент под действием силы тяжести, оказывающий воздействие на маятник, является нелинейной функцией его угла. Понять, почему это так, будет легче, если вы представите, насколько трудно держать гирю в вытянутой руке, расположенной под теми или иными углами по отношению к телу: рука опущена вертикально вниз, поднята на уровень плеч, поднята прямо над головой (вертикально вверх) и т. д. (В этом случае важно понимать разницу между весом и изгибающим моментом. В каком бы положении ни находилась гиря, сила тяжести остается одной и той же: она тянет вниз с силой, определяемой лишь весом гири. Но при некоторых значениях угла сила тяжести также изгибает вашу руку, выворачивая ее вниз. Изгибающий момент определяет величину этого эффекта изгибания.) Когда ваша рука опущена вертикально вниз, изгибающий момент полностью отсутствует, то есть ваша рука не изгибается. Если вы несколько отведете вытянутую руку в сторону, создав небольшой угол между вашим телом и вытянутой рукой, сила тяжести начнет оказывать на вашу руку небольшой изгибающий момент. Поначалу этот изгибающий момент увеличивается почти пропорционально углу. При отклонении руки на 2 градуса от вертикали изгибающий момент увеличивается практически в два раза по сравнению с изгибающим моментом при отклонении, равном 1 градусу. Считается, что при столь малых углах отклонения изгибающий момент является линейной функцией угла: удваивается угол, удваивается изгибающий момент. В этом случае график зависимости изгибающего момента от угла отклонения представляет собой практически прямую линию (отсюда термин линейная применительно к функции).

Однако эта приблизительная линейность нарушается при увеличении угла отклонения. Изгибающий момент увеличивается медленнее, чем можно было бы ожидать: значения изгибающего момента оказываются ниже прямолинейной экстраполяции, которой описывалась функция изгибающего момента при малых значениях угла отклонения. Максимальное значение изгибающего момента достигается, когда ваша рука вытягивается параллельно полу, под углом 90 градусов к вашему телу. Очень нелегко удерживать в таком положении гирю в течение долгого времени. Если поднять руку еще выше, над плечом, изгибающий момент начнет уменьшаться и достигнет нуля, когда ваша рука с гирей окажется вытянута вертикально вверх. Таким образом, график зависимости изгибающего момента от угла отклонения представляет собой что-то наподобие дуги: он наклоняется вниз. Этот график определенно носит нелинейный характер. На самом деле он представляет собой дугу синусоиды.

Теперь мы замечаем связь с переходом Джозефсона. Эта синусоидальная функция является точно такой же, с какой мы встречались ранее в эффекте постоянного тока Джозефсона, где сверхток демонстрировал пропорциональную зависимость от синуса фазы на переходе Джозефсона. Аналогия в данном случае заключается в том, что фаза на переходе Джозефсона ведет себя подобно углу отклонения маятника. Оказывается, что у всех остальных членов уравнения также имеются свои аналоги. Поток обычных электронов соответствует торможению маятника, вызываемому силой трения. Масса маятника подобна емкости перехода. А изгибающий момент, прикладываемый к маятнику, подобен внешнему току, управляющему переходом.

Такие механические аналогии всегда ценились в науке. Они делали незнакомое знакомым. В данном случае аналогия позволяет нам перенести наши интуитивные представления о маятниках на переходы Джозефсона. Например, когда переход Джозефсона пребывает в устойчивом состоянии, фаза постоянна. В этом случае динамические процессы отсутствуют, как отсутствует и предмет для изучения; переход Джозефсона ведет себя подобно идеальному сверхпроводнику, через который протекает только сверхток. Механическим аналогом перехода Джозефсона в устойчивом состоянии может служить маятник, изгибаемый в сторону постоянным по силе изгибающим моментом, пребывающий в неподвижности и отклоненный на угол, ниже горизонтали. Силы трения и инерции отсутствуют по причине отсутствия движения. Прикладываемый изгибающий момент компенсируется лишь силой тяжести. Этот простой случай имеет место лишь тогда, когда мы пропускаем через переход постоянный ток, меньший некой критической величины.

Гораздо больший интерес представляет ситуация, когда мы пропускаем через переход ток, превышающий критическую величину. В этом случае фаза начинает внезапно меняться во времени достаточно сложным образом. Как только начинается изменение фазы, на переходе возникает электрическое напряжение. Затем, вследствие эффекта переменного тока Джозефсона, сверхток начинает осциллировать туда и обратно между сверхпроводниками. Тем временем электрическое напряжение, возникшее на переходе, также вызывает прохождение через этот резисторный канал обычных, неспаренных электронов, тогда как ток смещения также пытается отвоевать свою долю совокупного тока. В результате активизируются все три канала. Их взаимодействие порождает запутанную картину снижений и нарастаний тока этих трех составляющих. Первопричиной всей этой сложности является нелинейная динамика фазы на переходе Джозефсона. Если попытаться воспользоваться механической аналогией, то мы должны нарисовать в своем воображении маятник, подвешенный на оси и вращающийся вокруг нее с переменной скоростью, застывая на мгновение в своем верхнем положении, ускоряясь в нижнем положении и в течение всего этого времени компенсируя прикладываемый изгибающий момент с переменными сочетаниями силы трения, силы тяжести и силы инерции.

Если же мы еще больше усложним ситуацию и предоставим возможность самому изгибающему моменту изменяться во времени, подобно вращению барабана стиральной машины то в одну, то в другую сторону, вращение нашего маятника может стать хаотическим, он может начать вращаться то в ту, то в другую сторону, причем эти перемены направления вращения могут стать бессистемными. Подтверждение возможности возникновения соответствующих электрических «спазмов» в переходе Джозефсона оказалось одним из первых экспериментальных триумфов в теории хаоса. До того времени физики привычно рассматривали маятник как символ точной и размеренной работы часового механизма. Внезапно он оказался парадигмой хаоса[160].

Принципиальным моментом является то, что динамика вращающегося маятника и перехода Джозефсона описывается одним и тем же уравнением и что это уравнение является нелинейным. Как подчеркивалось ранее, нелинейные задачи отличаются своей многогранностью, максимальной приближенностью к реальности и чрезвычайной сложностью. Нелинейные задачи представляют собой не только передний край математики, но и ее дальние горизонты. Важные достижения теории хаоса, которые пришлись на 1970-е и 1980-е годы (подробнее об этих достижениях рассказывается в следующей главе), расширили наши представления о динамике вращающегося маятника и перехода Джозефсона и позволили нам уяснить ее.

Связь между маятниками и переходами Джозефсона – лишь один из многих выдающихся мостов на ландшафте синхронизма. Я и мои коллеги недавно натолкнулись на еще один такой мост – возможно, еще более неожиданный. Этот мост связывает популяции биологических осцилляторов с динамикой переходов Джозефсона, соединенных между собой в большие массивы. Смысл этой связи остается для нас загадкой; тем не менее это, по-видимому, важная связь, поскольку она соединяет между собой два центральных предмета науки. Один из этих предметов касается древних наблюдений синхронизма в живой природе: деревьев, усеянных светлячками, в Таиланде и Малайзии, ночных хоров сверчков, суточных циклов растений и животных, задаваемых солнцем. Другой предмет касается изучения синхронизма в неживой природе, начиная с маятниковых часов Гюйгенса, симпатизирующих друг другу, и заканчивая (после длительного перерыва длиною в сотни лет) изобретением замечательных осцилляторов XX столетия: электрических генераторов и систем фазовой автоподстройки частоты, лазеров и транзисторов, а в последнее время – сверхпроводящих переходов Джозефсона. Несмотря на то что ученые уже давно догадались о склонности групп живых и неживых осцилляторов к самопроизвольной взаимной синхронизации, лишь в 1996 г. мы осознали, насколько могут быть схожи механизмы, лежащие в их основе. Оказалось, что эта схожесть имеет «семейственный» характер – признак одной и той же математической крови.

Эта связь была выявлена в ходе изучения массивов переходов Джозефсона[161] – архитектуры, которая соответствует следующему уровню в иерархии синхронизма. Мы уже обсуждали с вами низший, субатомарный уровень – тот, который рассматривал сам Джозефсон: триллионы синхронизированных куперовских пар электронов, когерентно совершающих перемещения туда и обратно через переход Джозефсона и создающих сверхток, который осциллирует сквозь изоляционный барьер перехода. Следующий этап заключается в том, чтобы объединить между собой многие из этих электронных осцилляторов в некий массив и исследовать синхронизацию между ними. Если воспользоваться одной из наших предыдущих аналогий, то куперовские пары электронов подобны отдельным скрипачам в оркестре, координирующим свои действия с целью образования хорошо сыгранной группы струнных инструментов – перехода Джозефсона. Затем несколько групп инструментов (струнные, духовые, ударные) объединяются в еще больший ансамбль – массив переходов Джозефсона. Однако в данном случае «дирижер» не предусматривается: предполагается, что массив переходов Джозефсона будет синхронизироваться самостоятельно.

Задача заключается в том, чтобы предсказать групповое поведение переходов Джозефсона с учетом того, что нам известно об индивидуальном поведении таких переходов. Этот вопрос очень важен, поскольку массивы переходов Джозефсона используются во многих современных технологиях, начиная с устройств сканирования головного мозга и других видов медицинского оборудования, применяемого для формирования изображений, и заканчивая детекторами электромагнитных излучений на длинах волн, представляющих интерес для специалистов по радиоастрономии и мониторингу загрязнений атмосферы. Так называемый стандартный вольт США (официальный стандарт напряжения, который позволяет лабораториям разных стран мира сравнивать получаемые ими результаты) поддерживается Национальным институтом стандартов и технологий США, использующим массив из 19 тысяч переходов Джозефсона, последовательно соединенных между собой. Разработчикам электронных схем хотелось бы уметь предсказывать оптимальную компоновку для массива, выполняющего какую-то определенную функцию, однако из-за «неподатливости» нелинейных уравнений, описывающих те или иные варианты массива, им приходится полагаться либо на интуицию, либо на хорошо известный метод проб и ошибок.

Теоретики пытаются предложить определенный метод для сведения таких уравнений к линейному виду за счет существенных упрощений. Этот прокрустов подход время от времени проливает свет на большинство симметричных видов коллективного поведения, например идеально синхронизированное состояние, при котором все переходы осциллируют строго синфазно и синхронно. Но в качестве исследовательского инструмента линейная теория совершенно непригодна. Она слишком близорука, чтобы дать нам представление об огромном множестве способов, с помощью которых может произойти самоорганизация массива.

Такой степени сложности задачи соответствует лишь нелинейная динамика, с ее акцентом на геометрию, визуализацию и глобальное мышление. Разумеется, рассмотреть все возможности одновременно, исследовать динамику сотен нелинейных уравнений, соответствующую математическому потоку в абстрактном n-мерном пространстве (где n может достигать нескольких сотен) – чрезвычайно сложная задача. Но примерно в 1990 г., принимая во внимание успехи, достигнутые теорией хаоса, специалисты по нелинейным проблемам были готовы к тому, чтобы взяться за решение этой задачи. Теоретики испытывали чувство уверенности и энтузиазм. К тому времени специалисты по математической биологии уже погружались в многомерные пространства, продвигаясь там буквально наощупь, пытаясь как можно лучше понять свои идеализированные модели сообществ светлячков, нейронов и клеток сердца. Это было новым подходом, который Курт Визенфельд, молодой физик из Технологического института штата Джорджия, хотел применить для анализа массивов Джозефсона.

К 1990 г. Курт Визенфельд уже сделал себе имя в науке. В 1987 г. он стал одним из авторов статьи, которую можно рассматривать как введение в концепцию «самоорганизующегося критического состояния»[162] – амбициозной теории, которая обещала объяснить, почему столь многие сложные системы, как кажется, постоянно балансируют на грани катастрофы. Эту теорию впоследствии применили для объяснения особых статистических картин, которые наблюдались в случаях массового вымирания, землетрясений, лесных пожаров и других сложных процессов, в ходе которых в системе распространяются эффекты домино, обычно вызывая небольшие каскадные последовательности событий, а в отдельных случаях – катастрофические последствия. Это была смелая работа, не лишенная ряда противоречий. Большинство физиков считали ее важным достижением в нашем понимании сложных систем, хотя некоторые скептики восприняли ее лишь как плод неуемной фантазии авторов. Один шутник назвал ее «самовозвеличивающей тривиальностью»[163].

В описываемое нами время Курт Визенфельд был научным сотрудником с ученой степенью в Брукхейвенской национальной лаборатории. Он занимал должность младшего профессора и подумывал над тем, чтобы приступить к самостоятельной разработке какой-то темы. Его уже давно увлекали связанные нелинейные осцилляторы; еще в начале своей работы над самоорганизующимся критическим состоянием он проявлял интерес к спаренным маятникам. Поэтому уравнения, описывающие массивы переходов Джозефсона, не были для него большой новостью: он чувствовал себя вполне комфортно с ними, поскольку они напоминали столь привычные ему задачи с маятником. Его приход в эту область начался с сотрудничества с Питером Хэдли, аспирантом Стэнфордского университета, и его консультантом Маком Бисли, специалистом по сверхпроводимости, который в то время уже пришел к выводу, что в нелинейной динамике есть многое, что можно было бы использовать для анализа массивов Джозефсона. Реализация их совместного проекта началась после того, как они заручились поддержкой Визенфельда. Это была высокопрофессиональная команда исследователей. Питер Хэдли был поистине неутомимым тружеником и изобретательным специалистом, поднаторевшим в вопросах компьютерного моделирования. Долговязый блондин Бисли отличался большой сообразительностью, практическим опытом и, что немаловажно, любил цитировать всевозможные афоризмы. Курт был общепризнанным авторитетом в области нелинейной динамики – на то время, пожалуй, одним из лучших специалистов в этой области.

Они решили сосредоточиться на «последовательных массивах», то есть массивах, в которых переходы Джозефсона соединены последовательно друг с другом. Архитектура такого рода была наиболее податлива с математической точки зрения; к тому же она представляла технологический интерес для применения в системах генерирования излучения. Несмотря на то что отдельно взятый переход Джозефсона вырабатывает излучение, мощность которого составляет примерно один микроватт – что совершенно недостаточно с практической точки зрения, – вырабатываемую мощность излучения можно существенно увеличить, соединив соответствующим образом множество переходов Джозефсона. Точно так же как синхронно хлопающая в ладони публика в зале производит гораздо больший шум, чем любой отдельно взятый зритель, синхронизированный массив переходов Джозефсона оказывается гораздо более мощным источником излучения, чем отдельно взятый переход. Если бы, например, вы могли придумать способ заставить синфазно осциллировать тысячу переходов Джозефсона, то мощность, подаваемая на какое-нибудь другое устройство – «нагрузку», подключенную параллельно такому массиву переходов, – увеличилась бы в миллион раз. (Совокупная мощность пропорциональна квадрату количества переходов.) Проблема, однако, заключается в том, как синхронизировать такой массив переходов. Никто не знает, какой должна быть оптимальная архитектура соответствующей цепи и какой вид нагрузки является самым подходящим для этого. Вообще говоря, на самом деле никто не знает, почему такие массивы должны – или вообще не должны – синхронизироваться. Это было фундаментальной проблемой для данной области знаний в целом.

Курту и его сотрудникам было известно, что важнейшую роль играют электрические характеристики нагрузки – то, как она препятствует прохождению электрического тока. (В случае полного отсутствия нагрузки переходы никогда не удалось бы синхронизировать; они даже не смогли бы ощущать электрические осцилляции друг друга.) Простейший вид нагрузки должен вести себя подобно резистору, пропуская через себя ток, пропорциональный напряжению на нагрузке. Он может вести себя подобно конденсатору (который блокирует постоянный ток, но пропускает переменный ток) или катушке индуктивности (которая обладает характеристиками, обратными конденсатору: пропускает постоянный ток, но оказывает сопротивление переменному току высокой частоты). Вообще говоря, нагрузка может представлять собой то или иное сочетание трех указанных видов сопротивления с разными весовыми коэффициентами – одним словом, выбирать было из чего.

Моделируя десятки разных вариантов на компьютере, исследователи определили характеристики устойчивости синхронизированного состояния[164] и выяснили, какие нагрузки лучше всего синхронизируют такой массив. По ходу дела они натолкнулись на факт, который изначально не являлся предметом их исследований; этот факт невозможно было не заметить. Когда такие массивы не были синхронизированы, они обычно упорядочивали свое поведение несколько иначе: все переходы осциллировали с одним и тем же периодом, но при этом были предельно рассинхронизированы между собой – так, словно они не хотели иметь ничего общего друг с другом. Исследователи назвали этот необычный режим организации состоянием антифазы; впоследствии для него было придумано другое название: разнесенное состояние (splay state).

В случае двух переходов это разнесенное состояние похоже на то, что наблюдал Гюйгенс, когда его часы пребывали во «взаимной симпатии»: маятники раскачивались с одной и той же частотой, но разность их фаз составляла половину цикла. Когда один маятник говорил тик, другой говорил так. В случае, когда количество переходов больше двух, разнесенное состояние делит цикл на равные части[165]. В случае 10 переходов они будут совершать идентичные движения, разнесенные между собой на десятую долю цикла. Все они движутся одинаково: одинаково совершают колебательные движения, но с определенным сдвигом по фазе друг относительно друга. Так и тянет представить это групповое поведение как изысканную хореографию: по массиву пробегает одна волна за другой. Однако такая аналогия вводила бы нас в заблуждение. Эта «волна» вовсе не обязательно пробегает строго последовательно по всему массиву переходов: они могут совершать свои «движения» в любом порядке. Если бы вместо электрических колебаний речь шла о механических колебаниях, то разнесенное состояние напоминало бы шеренгу танцующих роботов, причем все они исполняют одну и ту же последовательность колебательных движений, но упорядоченных в пространстве случайным образом: один робот совершает какое-то определенное движение, затем в дальнем конце шеренги другой робот совершает то же самое движение, затем в каком-то другом месте шеренги третий робот выполняет то же самое движение и т. д. Разрешены любые комбинации. Роботы могут танцевать в любом порядке, причем каждый из этих вариантов является допустимым разнесенным состоянием. Эти варианты отличаются друг от друга лишь упорядоченностью в пространстве, но не совершаемыми движениями или интервалами между действиями.

Чем больше массив, тем больше количество возможных перестановок, причем это количество растет очень быстро – даже быстрее, чем при нарастании по экспоненциальному закону. В случае 5 переходов существует 24 разнесенных состояния. В случае 10 переходов – 362 880 разнесенных состояний. Визенфельд полагал, что это лавинообразное нарастание может служить основой для разработки многообещающей архитектуры оперативной памяти для будущего компьютера Джозефсона. Каждая память может храниться как особое разнесенное состояние. Вместо статического сочетания «нулей» и «единиц» память кодировалась бы как некая динамическая картина, хоровод электрических состояний в массиве. (Специалисты по нейронным сетям полагают, что примерно так функционирует наша память на запахи; в этом случае осцилляторами являются нейроны в обонятельной луковице головного мозга, а разные шаблоны возбуждения кодируют разные запахи.)

Используя буквально несколько переходов Джозефсона, вы можете создать гигантскую, сколь угодно большую память. Есть лишь одна проблема: чтобы такая схема заработала, каждое состояние должно быть устойчивым, чтобы исключить влияние случайных шумов в электронных схемах. Таким образом, главный вопрос заключается в том, устойчивы ли разнесенные состояния? И как эта устойчивость зависит от нагрузки? В то время Визенфельду не удалось решить эту задачу математически. Более того, он осознал, что ему все еще не хватает глобального понимания. Какие еще факторы, помимо синхронизированных состояний и разнесенных состояний, могут оказывать влияние на соответствующие процессы? И каково совместное влияние всех этих факторов? Визенфельд поставил перед собой амбициозную цель: уяснить все возможные виды коллективного поведения для любого количества переходов, соединенных последовательно – и параллельно любому виду нагрузки.

Когда я познакомился с Визенфельдом в 1990 г. на одной из конференций в Техасе, между нами сразу же установилось полное взаимопонимание. Мы были людьми примерно одинакового возраста, в наших биографиях было много общего, у нас были примерно одинаковые научные интересы. К тому же оказалось, что вместе мы много смеемся. После того как он рассказал мне о своем видении проблемы массивов Джозефсона, я полагал, что нам было бы интересно работать над этой проблемой вместе. Курт, который, возможно, чувствовал свою личную ответственность за то, что увлек меня этой работой, напомнил мне о ее возможных технологических применениях (это нужно было знать на тот случай, если кто-нибудь спросит у меня, почему я выбрал именно это направление исследований, а не какое-то другое). Но, честно говоря, технологические применения не были реальной причиной того, почему эти переходы так интересовали меня и Курта. Главной причиной было чистое любопытство, а также предвкушаемое нами удовольствие от создания математического описания восхитительной системы связанных осцилляторов.

Особенно заманчивыми казались нам сами уравнения. Каждый переход был связан со всеми остальными переходами, причем все эти связи были идентичны. Несмотря на то что физически они были соединены между собой последовательно, подобно звеньям длинной цепи, уравнения сделали их похожими на систему, все элементы которой соединены между собой по принципу «каждый с каждым». Это удивило и восхитило меня. Я был уже знаком с этим странным сверхсимметричным видом соединения по моей предыдущей работе над моделью клеток сердца, предложенной Пескином, а также моделями биологических осцилляторов Уинфри и Курамото. Тогда соединение по принципу «каждый с каждым» было выбрано нами исключительно из соображений целесообразности. Никто не знал, как в действительности должны выглядеть уравнения, поэтому нам представлялось вполне естественным начать с простейшего случая. Разумеется, это была, так сказать, карикатура: реальные клетки сердца и светлячки взаимодействуют сильнее со своими соседями, чем с теми, кто находится вдалеке.

Поэтому когда точно такое же соединение по принципу «каждый с каждым» появилось в уравнениях, описывающих массив Джозефсона, я понимающе ухмыльнулся. Вот она, стандартная аппроксимация. «Нет-нет, – сказал мне Курт, – именно так все обстоит в действительности: в данном случае соединение по принципу “каждый с каждым” является не аппроксимацией, а реальностью». Такой принцип соединения проистекает непосредственно из уравнений цепи[166] и является следствием того факта, что в случае, когда переходы соединены между собой последовательно, через каждый из них протекает одинаковый ток, подобно ведрам воды, которые передают по цепочке люди на пожаре. Он обещал отправить мне по завершении конференции подробное письмо с описанием процессов, происходящих в такой цепи.

Еще до того как я вскрыл конверт, по почерку, каким был написан мой адрес на конверте, я понял, что работа с Куртом доставит мне подлинное удовольствие. Курт отличался безупречным каллиграфическим почерком: каждая буковка выглядела аккуратно и даже элегантно, точно по своим очертаниям и в то же время прихотливо. Принимая в течение многих лет экзамены у аспирантов, я научился делать определенные выводы о характере человека на основе особенностей его почерка и, должен сказать, что мой метод анализа почерка, пусть и непрофессиональный, ни разу не подвел меня: в тех случаях, когда аспирант выводил маленькие аккуратные буковки, что-то наподобие печатного шрифта, я почти не сомневался в высоком уровне его знаний. Это правило, между прочим, ничего не говорит о корявом почерке. Знания аспиранта, который царапает свои ответы как курица лапой, могут быть либо весьма посредственными, либо блестящими, либо какими угодно в этом диапазоне. Но каллиграфический почерк… Нет, такой почерк – всегда хороший признак.

Курт предложил начать с самого простого, идеализированного варианта: двух идентичных переходов Джозефсона, соединенных последовательно и управляемых постоянным током. Допустим, нагрузкой является резистор – опять-таки, самый простой вариант, – а вместо обычных трех каналов, по которым проходит ток в каждом из переходов Джозефсона, действуют лишь два канала: один для сверхтока, а другой для обычного тока. (В случае определенных видов переходов третьим каналом – по которому проходит ток смещения – можно пренебречь, что будет вполне допустимой аппроксимацией.)

Преимущество этих упрощений заключалось в том, что это позволяло нам визуализировать динамику системы, создавая обычные двумерные представления. В любой данный момент каждый переход характеризовался вполне определенной фазой – точно так же, как маятник, сфотографированный в какой-то момент времени, находится под определенным углом к вертикали. Представляя в графическом виде одну фазу по горизонтальной оси, а другую – по вертикальной, мы можем изобразить все возможные сочетания в виде соответствующих точек в неком квадрате, стороны которого соответствуют 360 градусам возможных фаз. Этот квадрат называется «пространством состояний» системы. Он обладает замечательным геометрическим свойством, навевающем воспоминания о старых видеоиграх, в которых космический корабль, уходящий за правый край экрана, чудесным образом появляется из-за левой границы, а космический корабль, ударяющийся о нижний край экрана, возникает наверху. Пространство состояний для этого массива Джозефсона должно было обладать таким же свойством, поскольку фаза, составляющая 360 градусов, физически неотличима от фазы, равной 0 градусов (точно так же как маятник, свисающий вертикально вниз, будет все так же свисать вертикально вниз, если повернуть его вокруг оси на 360 градусов). Поскольку левый и правый края квадрата соответствуют одному и тому же физическому состоянию, математики представляют их как полностью слившиеся в одну линию, как если бы вы свернули лист бумаги в цилиндр, соединив между собой его края. Кроме того, верхний и нижний края квадрата также соответствуют одному и тому же физическому состоянию, поэтому их также следует соединить между собой, а это означает, что верхний и нижний края нашего цилиндра также нужно соединить между собой, в результате чего получится что-то похожее на жареный пончик, поверхность которого представляет собой форму, называемую тором.

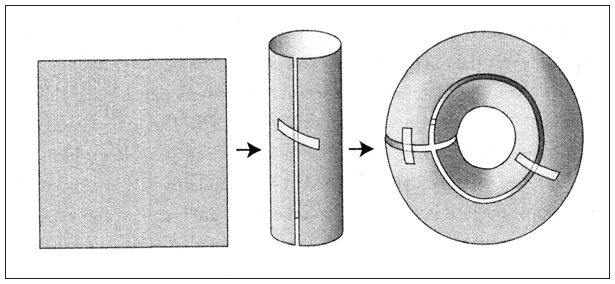
Таким образом, мы приходим к выводу, что пространство состояний для этого простейшего из массивов Джозефсона эквивалентно поверхности тора. Каждая точка на поверхности такого тора соответствует определенному электрическому состоянию массива, и наоборот. По мере того как с течением времени массив переходит из одного состояния в другое, точка, соответствующая электрическому состоянию массива, плавно перемещается по поверхности тора, подобно тому как увлекается плавным течением ручейка пылинка, случайно оказавшаяся на его поверхности. Картина течения этого воображаемого ручейка – со всеми его изгибами и завихрениями, его заводями и участками с ускоряющимся течением – учитывается в уравнениях цепи для нашего массива. Исходя из текущих значений фаз, эти уравнения определяют, как изменятся фазы в следующий момент времени.

Эти уравнения относятся к классу нелинейных уравнений, поэтому мы, конечно, не могли надеяться на то, что нам удастся найти для них однозначное и исчерпывающее решение, но мы полагали, что сможем выяснить качественные характеристики этого потока в целом. Например, точки стагнации (места на поверхности тора, где наша воображаемая пылинка застревает) должны соответствовать состояниям электрического равновесия для массива, когда все токи и напряжения не изменяются во времени. Устойчивость таких состояний можно оценить, вообразив, как наша пылинка могла бы покинуть такое состояние: если она всегда возвращается в него, как если бы ее засасывало в водосток, то такое состояние равновесия является устойчивым. Можно также предположить, что картина потока содержит замкнутый контур, маленький водоворот, в котором наша пылинка может кружиться до бесконечности, каждый раз по истечении определенного времени возвращаясь в свою исходную позицию. Такой контур должен означать некую форму периодического, повторяющегося поведения – электрическую осцилляцию в массиве. Мы с Куртом были уверены, что такие контуры обязательно должны иметь место, но нам не было ничего известно об их устойчивости – о том, всасывают ли они в себя соседние состояния.

Простейшим контуром является синхронная осцилляция, при которой фазы обоих переходов все время остаются равными. Соответствующая траектория пролегает вдоль главной диагонали квадрата. Она начинается в нижнем левом углу, затем движется на северо-восток, пока не достигнет верхнего правого угла, после чего она мгновенно возвращается в нижний левый угол (поскольку 360 градусов и 0 градусов соответствуют одной и той же фазе). Если рассматривать такую траекторию на квадрате, то получается, что она все время перепрыгивает из одного угла в другой, но если ее рассматривать на поверхности тора – которая представляет собой истинное пространство состояний для нашей системы, – то никаких перепрыгиваний не наблюдается. Переход оказывается плавным и незаметным.

Когда мы проанализировали картину этого потока в целом, мы были потрясены, обнаружив, что каждая другая траектория повторяет себя подобным образом. Каждое решение является периодическим. Если же вглядеться в эту картину пристальнее, то ничего особенно удивительного в обнаруженном нами факте нет. Качающийся маятник все время повторяет свое поведение, по крайней мере в простейшем, идеализированном случае, когда в его подшипниках отсутствует сила трения и когда отсутствует сопротивление воздуха. В этом случае не имеет значения, инициируете ли вы процесс колебаний маятника с большой или с малой дуги – в любом случае колебания будут оставаться неизменными и повторяться до бесконечности. То же самое относится ко всем другим видам «консервативных» механических систем, гипотетических идеализированных случаев, где отсутствуют какие бы то ни было формы трения и рассеяния механической энергии, а вся эта энергия полностью сохраняется («консервируется»), не превращаясь в тепло. Однако именно по этой причине периодическое поведение массива Джозефсона оказалось для нас столь неожиданным. Этот массив был нагружен трением. С электрической точки зрения, трение – это сопротивление. Сами переходы Джозефсона заключают в себе сопротивление (соответствующее пути, по которому проходит обычный ток), а нагрузкой цепи служил обычный резистор. Тем не менее этот массив воплощал в себе консервативную систему.

Мы с Куртом хотели понять, является ли столь парадоксальное поведение результатом изучения нами лишь двух переходов. Возможно, когда мы приступим к изучению большего числа переходов, система, так сказать, расправит свои крылья и продемонстрирует более представительный диапазон поведения. Я располагал рядом старых компьютерных программ, которыми пользовался при выполнении своей предыдущей работы по биологическим осцилляторам для имитации моделей Уинфри и Курамото, с сотнями цветных точек, бегущих по окружности, а также компьютерной программой для модели клеток сердца, разработанной Пескином; напомню, что тогда нам здорово помогло стробирование системы каждый раз, когда срабатывал один из ее осцилляторов. Все эти программы можно было легко адаптировать к уравнениям, описывающим поведение массива Джозефсона. После того как Курт вернулся к работе в Технологическом институте штата Джорджия, а я – в МТИ, имело смысл разделить наши усилия. Курт вместе со своим аспирантом по имени Куок Цанг занялся математическим анализом в случае, когда число переходов больше двух, а я приступил к компьютерному моделированию[167].

Для начала мы решили рассмотреть случай с десятью переходами. Такое количество переходов представлялось нам вполне обозримым, однако визуализировать случай со столь большим количеством переходов было очень непростым делом: вместо потока на квадрате или на поверхности тора траектории теперь пролегали в 10-мерном пространстве. Мои компьютерные программы неустрашимо ринулись в бой, продираясь сквозь нелинейные уравнения для 10-мерного пространства, продвигаясь к цели буквально крошечными шагами и отображая изменяющиеся фазы переходов в виде 10 точек, бегущих по окружности. Полученные изображения потрясли меня своей запутанностью и невразумительностью. Точки кружились и завихрялись, оставляя ошеломительное впечатление бесконечного хоровода, на основании которого, однако, невозможно было прийти к какому-то определенному заключению. Особенно трудно было проследить какие-либо постепенные изменения в относительном позиционировании. Немного легче стало после того, как я решил прибегнуть к испытанному приему со стробированием. Когда какой-то заранее выбранный переход достигал определенной фазы, происходила воображаемая вспышка, которая высвечивала фазы остальных девяти переходов. Это, конечно, помогло справиться с кружением огромного количества точек, однако оставались 9 точек, которые нужно было отслеживать одновременно. Необходимость отслеживания 9 точек означала необходимость визуализировать 9-мерное пространство.

Человеческий мозг не в состоянии легко визуализировать более трех измерений, а плоский экран компьютера вообще ограничивал картинку лишь двумя измерениями. Мне нужно было каким-то образом расширить свое сознание, попытаться представить, что происходит в этом странном 9-мерном мире. Немного поэкспериментировав, я остановился на мультипанельном формате, характерном для фильмов 1960-х годов, где на разных участках экрана («панелях») демонстрировались изображения разных актеров, причем каждому актеру отводился свой участок экрана. На одной панели отображалась фаза перехода № 2 в функции фазы перехода № 3, причем на одной оси были представлены значения фазы перехода № 2, а на другой – значения фазы перехода № 3. На других панелях отображались аналогичные зависимости между фазами переходов 3 и 4, 5 и 6 и т. д. Переход № 1 предназначался для запуска строба: когда он пересекал некую исходную линию (определенная фаза в его цикле), компьютер отображал соответствующую точку на каждой панели, представляя одновременные фазы в данный момент. В результате компьютерный экран заполняли панели, регулярно обновляемые после каждой стробоскопической вспышки.

Прежде чем взглянуть на систему из десяти переходов этими новыми теоретическими глазами, мне нужно было подготовиться к тому, что я мог увидеть. В наихудшем случае, если решения соответствующих нелинейных уравнений окажутся невероятно сложными, точки на каждой панели будут появляться то здесь, то там, постепенно заполняя собою некое аморфное тело. Если они будут заключать в себе некое подобие структуры, то это тело может быть похоже на кружево, испещренное бороздками. Или, если все окажется таким же на удивление простым, как в случае с двумя переходами, каждая очередная точка будет долбить в одно и то же место экрана (может, даже просверлит в нем дырку), никогда не покидая пределов пиксела, в котором она изначально появилась. Это беспрестанное повторение сигнализировало бы о том, что все траектории по-прежнему являются периодическими (поскольку в случае периодического решения каждый раз, когда переход № 1, пересекая исходную линию, запускает вспышку, переходы № 2 и № 3 всегда оказываются на своих местах – и так на любой другой панели).

Я включил компьютер и уставился на экран. Спустя какое-то время на каждой из панелей одновременно появилось по одной точке; это означало, что переход № 1 завершил один «круг» и зажег свой строб. Затем еще один круг, и еще один. На каждой из панелей точки «приземлялись» вблизи мест, где появилась первая точка, но не строго поверх первой точки. Что ж, это уже интересно! Эти неточные попадания означали, что траектории для 10 переходов не являются периодическими, а это, в свою очередь, подтверждало наши подозрения о том, что случай с двумя переходами является особым случаем, который не может служить надежным указанием на то, чего нам следует ожидать в случае большего количества переходов.

В ходе дальнейшего моделирования ситуации с 10 переходами начала вырисовываться несколько иная картина. Точки начали складываться в некую кривую, а вовсе не в ожидаемое мною аморфное тело, причем их движение казалось очень тщательно выверенным, прочерчивая траекторию, тонкую, как лезвие бритвы, удлиняя ее и заполняя в ней пустоты. Все панели показывали разные версии одной и той же базовой структуры: контур с несколько искаженной треугольной формой и скругленными углами. Я засомневался, не выбрал ли я ненароком слишком уж нехарактерную исходную точку. Поэтому я испытал много разных начальных условий. Когда я увидел результаты, моему удивлению не было границ. Каждая исходная точка приводила к появлению ее собственного треугольника со скругленными углами, причем все отдельные треугольники точно укладывались друг в друга, подобно русской матрешке.

Это была поистине невероятная структура. Она означала, что в уравнениях заключена некая тайная симметрия, скрытая регулярность, которая должна быть причиной этого порядка. Мне еще никогда не приходилось видеть чего-либо подобного. Каждая траектория предоставляла для исследования невообразимо обширный, 10-мерный ландшафт, по которому можно было перемещаться вверх и вниз, влево и вправо, а также еще в семи измерениях, для обозначения которых нам даже не хватает слов, но которые, тем не менее, существовали. Это было так же невероятно, как ходить до бесконечности по натянутому канату, никогда не рискуя упасть. Было что-то такое, что сводило эти решения к некоему срезу всех возможностей. Я мог сколь угодно наращивать количество переходов в массиве – 20, 50, 100 – это не имело никакого значения. В любом случае получалась одна и та же картина русской матрешки: вложенные друг в друга треугольники. Когда я сообщил Курту эту новость, он был изумлен не меньше моего. Либо компьютер нехорошо пошутил над нами, либо мы столкнулись с беспрецедентной ситуацией в математике массивов Джозефсона.

В течение следующих четырех лет многие из нас буквально помешались на этих чудесах. Курт вместе со своим аспирантом Стивом Николсом выполнили компьютерное моделирование более широкого класса массивов, обнаруживая каждый раз одни и те же признаки удивительного порядка. Джим Свифт, математик из университета Северной Аризоны и приятель Курта по аспирантуре, придумал весьма остроумный способ аппроксимации уравнений[168], которые описывали динамику таким массивов, заменив их так называемыми усредненными уравнениями, которые было гораздо легче анализировать, но в которых, тем не менее, сохранялась суть исходных уравнений. (Подобно всем любителям решать загадки, математики зачастую пользуются аппроксимациями, когда рассматриваемая ими задача кажется чересчур сложной, чтобы ее можно было решить «в лоб», – по крайней мере на начальном этапе.) Упростив решение нашей задачи, Джим обеспечил возможность ее математического анализа. Следуя его примеру, мой аспирант Синья Ватанабе обнаружил признаки структуры «русской матрешки» в решениях усредненных уравнений Джима[169]; затем, проявив свое аналитическое мастерство, он смог доказать, что примерно такая же структура скрывается в исходных, не усредненных уравнениях цепи. Венцом всей этой истории стало открытие новой «интегрируемой системы», что является большой редкостью в математике. У нее нет каких-либо конкретных применений – по крайней мере из того, что нам известно на сегодня. Это открытие Ватанабе скорее похоже на находку какой-то красивой раковины на берегу моря.

Одной из самых замечательных особенностей исследований, проводимых исключительно из любопытства, – помимо, конечно, удовольствия, которое они доставляют самому исследователю, – является то, что нередко они приводят к неожиданным побочным результатам. Методы, разработанные Свифтом и Ватанабе, позволили нам впервые исследовать динамику массивов Джозефсона в более реалистичном случае, когда переходы не идентичны. Инженерам никогда не удавалось проанализировать неупорядоченные массивы, хотя им было хорошо известно о том, что электрические характеристики реальных переходов всегда отличаются друг от друга хотя бы на несколько процентов и что современные технологии производства переходов не позволяют обеспечить их полную идентичность. Такая вариабельность переходов ограничивает возможность их использования в массивах, поскольку она препятствует когерентному функционированию, которая является необходимым условием нормальной работы массивов Джозефсона. Когда такими массивами управляют внешние токи, поведение эих массивов отличается непостоянством: при токах ниже определенного порога они остаются некогерентными (все переходы осциллируют с произвольными фазами, что приводит к деструктивному взаимовлиянию напряжений на переходах и их взаимной компенсации), но после превышения этого порога массив самопроизвольно синхронизируется. Пытаясь уяснить такое поведение, мы с Куртом и его другом Пьером Коле воспользовались методом усреднения, предложенным Джимом, чтобы привести наши уравнения к более приемлемой для анализа форме.

Именно здесь нам на помощь пришла модель Курамото[170], ключ к синхронизму. До того времени модель Курамото считалась не чем иным, как удобной абстракцией, простейшим способом понимания того, как – и при каких условиях – группы несхожих между собой осцилляторов могут самопроизвольно синхронизироваться. Модель Курамото была исключительно плодом воображения, придуманным для использования в качестве весьма приблизительной модели биологических осцилляторов: сверчков, светлячков, клеток-ритмоводителей сердечного ритма. Теперь нам предстояло использовать ее для анализа динамики сверхпроводящих переходов Джозефсона. Это напомнило мне об удивительном чувстве, о котором в свое время говорил Эйнштейн: о чувстве, которое испытывает ученый, обнаружив скрытое единство явлений, которые прежде казались никак не связанными между собой.

Вскоре после того как мы опубликовали эти результаты, я получил из Киото (Япония) письмо, написанное красивым почерком. «Я испытал удивление и подлинное восхищение, – писал мне Йосики Курамото. – Я даже не мечтал о том, чтобы моя простая модель могла пригодиться для анализа реальных физических систем».

Модель Курамото была тем решением, которое терпеливо ожидало появления задачи, подходящей для себя. Она никогда не задумывалась своим создателем как буквальное описание чего бы то ни было. Она лишь представляла собой идеализированную модель, предназначенную для исследования рождения спонтанного порядка в его простейшей форме. Тем не менее обнаруженная связь ее с массивами Джозефсона тотчас же объяснила, почему эти приборы должны синхронизироваться резко, мгновенно. Этот фазовый переход был, по сути, тем же фазовым переходом, который открыл Уинфри в своей модели биологических осцилляторов и который впоследствии был столь элегантно формализован Курамото в его модели, поддающейся решению. Специалисты по переходам Джозефсона наблюдали этот переход еще раньше, в ходе компьютерного моделирования, выполнявшегося ими, однако не располагая теоретической основой для его понимания, они просто не обращали внимания на него (это еще раз напоминает нам известную истину: никогда не следует доверять какому-либо факту до тех пор, пока этот факт не будет подтвержден теорией).

После 1996 г. модель Курамото применялась для исследования других физических объектов, начиная с массивов связанных лазеров[171] и заканчивая гипотетическими осцилляциями легчайших субатомных частиц, называемых нейтрино[172]. Возможно, мы улавливаем первые признаки глубокого единства в природе синхронизма. Найдутся ли какие-либо практические применения этого единства, покажет будущее. Учитывая то, сколь многие болезни человека связаны с синхронизмом и его нарушениями (эпилепсия, сердечная аритмия, хроническая бессонница) и сколь многие устройства основаны на использовании синхронизма (массивы Джозефсона и массивы связанных лазеров, электроэнергетические системы, глобальная система навигации и определения местоположения), мы можем с уверенностью утверждать, что углубленное понимание спонтанного синхронизма обязательно приведет нас к появлению его практических применений.

Широкое использование модели Курамото поднимает вопрос о причинах вездесущести этой конкретной математической структуры. По правде говоря, она, наверное, вовсе не вездесуща. Я уделил ей так много внимания лишь потому, что она является, пожалуй, единственным случаем спонтанного синхронизма, который мы понимаем достаточно хорошо. Руководствуясь теоретическими положениями, можно показать, что модель Курамото применима лишь при выполнении четырех особых условий; в противном случае эта модель неприменима. Во-первых, рассматриваемая система должна состоять из огромного количества компонентов, каждый из которых является самоподдерживающимся осциллятором.

Это само по себе является сильным ограничением. Отдельным элементам должна быть присуща чрезвычайно простая динамика: чистая ритмичность на протяжении стандартного цикла, без хаоса, турбулентности и каких-либо осложнений – просто повторяющееся движение. Во-вторых, осцилляторы должны быть слабо связанными – в том смысле, что состояние каждого из них можно охарактеризовать только его фазой. Если же связь между осцилляторами настолько сильна, что способна существенно исказить амплитуду осциллятора, то модель Курамото неприменима. Третье условие накладывает наиболее сильные ограничения: каждый из осцилляторов должен быть связан в одинаковой степени со всеми остальными. На практике лишь очень немногие системы удовлетворяют этому условию. Вообще говоря, осциллятор взаимодействует сильнее со своими соседями в пространстве (или с совокупностью виртуальных соседей, определяемой некоторой сетью взаимного влияния). Наконец, осцилляторы должны быть практически идентичны, а величина дисперсии в их свойствах должна быть соизмерима со слабостью связи между ними.

С учетом всех этих условий динамика модели Курамото и родственных ей моделей должна становиться для вас самоочевидной. Тем не менее внезапное возникновение синхронизма по-прежнему оказывается для нас неожиданностью. Даже после того как синхронизм появляется, наше понимание его (и особенно понимание того, почему он возникает практически одномоментно и самопроизвольно) оказывается совершенно недостаточным. Последней иллюстрацией этого факта является фиаско лондонского моста Millenium Bridge.

Millenium Bridge должен был стать гордостью Лондона[173]. Этот элегантный авангардистский пешеходный мост, строительство которого обошлось лондонской казне более чем в 27 миллионов долларов, был первым за столетие новым мостом через Темзу в Лондоне. Он связывал лондонский район Сити и собор Св. Павла, расположенный на северном берегу Темзы, с музеем современного искусства Tate Modern, расположенным на южном берегу. Этот мост отличался радикальностью своей конструкции: самый плоский в мире висячий мост, волнистая лента длиной 320 метров с низкорасположенными консольными балками и тонкими стальными тросами, протянутыми через реку. Концепция такого моста стала плодом необычного сотрудничества между строительной компанией Ove Arup, архитектором лордом Норманом Фостером и скульптором сэром Энтони Каро. «Луч света, – так окрестил этот мост лорд Фостер, находясь под впечатлением его ночного вида, когда сооружение подсветилось многочисленными электрическими фонарями. – Нечто подобное, то есть конструкцию, создающую иллюзию свободного парения в воздухе, мы и намеревались создать»[174]. Хотя за строительство моста и его надежность отвечали инженеры компании Ove Arup, лорд Фостер и сэр Энтони были, по-видимому, также непрочь искупаться в лучах славы. Как бы то ни было, во время телетрансляции торжественного открытия моста, в котором участвовала королева, их лица сияли от удовольствия.

Открытие моста для публики состоялось в субботу, 10 июня 2000 г. Как только полиция разрешила, сотни возбужденных лондонцев ринулись на мост с обоих его концов. Однако буквально через несколько минут мост начал угрожающе раскачиваться из стороны в сторону; 690 тонн стали и алюминия выписывали в воздухе S-образные кривые, подобно извивающейся змее. Испуганные пешеходы судорожно цеплялись за перила, пытаясь удержаться на ногах, однако мост раскачивался все сильнее и сильнее. В конце концов амплитуда достигла 20 сантиметров.

Роджер Ридсдилл-Смит, один из молодых инженеров компании Ove Arup, который предложил эту новаторскую конструкцию, растерянно наблюдал за происходящим по ту сторону кордона, образованного полицейскими. Нет, такого не должно было случиться. Мысли вихрем проносились у него в голове. Компьютерное моделирование, оценки надежности и эксперименты в аэродинамической трубе не предсказывали ничего подобного. Надежность моста не вызывала у него сомнений. Мост Millenium Bridge не должен был разрушиться, подобно мосту Tacoma Narrows Bridge, печально известной «Галопирующей Герти», предсмертная агония которой запечатлена на старых кинопленках.[175] На этих записях видно, как судорожно изгибается мост под напором ветра, разрушаясь под воздействием торсионных колебаний. Тем не менее что-то заставляло Millenium Bridge резонировать. Полиция перекрыла доступ на мост, но он продолжал раскачиваться. Уже в понедельник, 12 июня, то есть через два дня после открытия, растерянные и сконфуженные городские власти были вынуждены закрыть мост Millenium Bridge.

Критики первоначального проекта полагали, что «Луч света» настигло заслуженное возмездие. Лорд Фостер уже не рассчитывал на благодарность со стороны лондонцев: осаждаемый журналистами, он выдавил из себя лишь несколько нелестных слов о строителях моста, с которыми ему пришлось сотрудничать. Строительная компания Ove Arup сразу же приступила к тестированию вибрационных характеристик моста в надежде понять, какая ошибка была допущена ими[176]. Они прикрепили к мосту огромные вибромашины и начали систематические испытания на разных частотах вибрации. Когда к мосту приложили горизонтальные вибрации с частотой, равной примерно одному циклу в секунду, он начал выписывать такие же S-образные кривые, какие наблюдались в день открытия.

Это было ключом к разгадке. Один цикл в секунду – это половинная частота ходьбы человека в обычном темпе. Проектировщикам моста известно, что обычный темп ходьбы человека – это примерно два шага в секунду, но основной эффект этих повторяющихся шагов заключается в создании вертикального, а не бокового усилия, поэтому ходьба не может быть причиной поперечных раскачивания моста. Внезапно инженеров осенила догадка: люди действительно с каждым шагом создают небольшое боковое усилие: когда вы ставите на землю правую ногу, вы отталкиваетесь по-одному, а когда ставите на землю левую ногу, вы отталкиваетесь по-другому. Эти попеременные боковые усилия создают колебания, частота которых примерно равняется половинной частоте ходьбы человека, то есть одному циклу в секунду, а не двум. Никто даже не задумывался над этим фактом: это не предусматривалось стандартными инструкциями для проектировщиков мостов в Великобритании. Как бы то ни было, эти боковые усилия невелики, а поскольку люди, передвигающиеся по мосту, как правило, не шагают в ногу, все боковые усилия, направленные влево и вправо, возникают в произвольные моменты времени и, следовательно, компенсируют друг друга. Но если по какой-то причине люди начнут шагать синхронно, все боковые усилия будут суммироваться и концентрироваться. Это, конечно же, может вызвать проблемы.

Инженеры еще раз просмотрели видеозапись телевизионного репортажа с открытия моста и увидели, что произошло именно то, что и должно было случиться. Когда мост начал раскачиваться, пешеходы инстинктивно скорректировали темп своей ходьбы, подсознательно синхронизировав его с ритмом раскачивания моста. Это лишь усилило вибрацию, что, в свою очередь, привело к тому, что еще большее число людей начало терять равновесие и дружно смещаться то в левую, то в правую сторону, обеспечивая таким образом еще больший взаимный синхронизм и тем самым еще больше усиливая вибрацию. Это была своего рода цепная реакция – положительная обратная связь между людьми и мостом. Наступление такой цепной реакции, которая привела к опасному раскачиванию моста Millenium Bridge, никто из проектировщиков не предвидел.

Этот вид резонансного эффекта отличается от другого хорошо известного резонансного эффекта, наличие которого заставляет солдат, вступая на мост, переходить со строевого шага на обычный, чтобы избежать создания в мосту опасных вибраций. Солдаты, проходя по мосту строевым шагом, действуют синхронно, тогда как пешеходы шагают по мосту вразнобой; во всяком случае, у проектировщиков моста не было никаких оснований предполагать, что пешеходы спонтанно начнут шагать по мосту в ногу. Они, конечно, учитывали возможность того, что какая-нибудь группа вандалов может пройти по мосту строевым шагом, и предусмотрели на этот случай определенный запас прочности, но им никогда не приходило в голову, что толпа из 2000 вполне благонамеренных пешеходов может по чистой случайности синхронизировать свое продвижение по мосту.

До сих пор неясно, что именно инициировало синхронизм в день открытия моста. Скорее всего, ядро синхронизма возникло случайно: как только толпа оказывается достаточно большой, всегда существует вероятность того, что на какой-то стадии достаточное число людей совершенно случайно начнут шагать синхронно, будет превышен определенный критический порог и мост начнет слегка раскачиваться. Как только это случится, в действие вступит эффект обратной связи, который лишь усилит раскачивание.

Дальнейшие исследования, выполненные инженерами компании Ove Arup, показали, что цепная реакция такого рода возможна лишь в случае достаточно длинного, гибкого и заполненного людьми моста – изменчивое сочетание ингредиентов, которое сложилось в тот день на Millenium Bridge. В частности, инженеры пришли к выводу, что никаких поводов для беспокойства нет, если количество людей на мосту не превышает указанного порогового значения. Так не бывает, чтобы мост слегка покачивался в случае небольшого количества людей, а по мере увеличения количества людей постепенно наращивал амплитуду своего раскачивания. Мост либо вообще не раскачивается, либо, как только будет превышен критический порог, он начинает раскачиваться угрожающе и без какого-либо предупреждения. Подобно соломинке, которая ломает хребет верблюда, начало опасного раскачивания моста представляет собой нелинейное явление.

Вообще говоря, во многом это похоже на фазовый переход, предсказанный моделями Уинфри и Курамото. Как следует из соответствующих теоретических представлений, осцилляторы (в данном случае – шаги пешеходов по мосту) некогерентны, если критический порог не превышен. Создаваемые ими усилия взаимно компенсируются. Они остаются некогерентными, даже когда связь между ними усиливается: когерентность не нарастает постепенно. Затем, внезапно, как только сила связи превысит определенное пороговое значение (поскольку на мосту находится количество людей, способное раскачать его в достаточной степени), синхронизм наступает практически одномоментно.

Здесь можно заметить еще один аспект концептуального единства. Мост Millenium Bridge представлял собой случай синхронизма, наведенного слабой связью через некого посредника. Эта тема, пусть и в неявном виде, проходит сквозной нитью через несколько последних глав. Взаимодействия пешеходов опосредовались вибрациями, которые они наводили в мосту, примерно так же, как маятники Гюйгенса чувствовали друг друга, производя вибрации в доске, с которой они свисали. В случае сверхпроводимости куперовские пары образуются потому, что электроны несколько деформируют пространственную решетку атомов; эта деформация создает между ними слабое притяжение точно так же, как шар для игры в боулинг, катящийся по матрацу, наполненному водой, увлекает за собой, в свой «кильватер», другой такой же шар. Такой же механизм действует даже в массиве переходов Джозефсона, соединенных последовательно друг с другом: переходы взаимодействуют между собой только из-за электрических осцилляций, которые они наводят в нагрузке. Отдельные осцилляторы во всех четырех случаях являются совершенно разными – электроны, маятники, высокотехнологичные приборы, люди, – однако механизм синхронизации во всех случаях остается, по сути, одним и тем же.

Основной момент этого объяснения был подтвержден инженерами компании Ove Arup после нескольких месяцев тщательного тестирования, в котором не только были задействованы огромные установки по созданию механических вибраций, но и проводились управляемые эксперименты с людьми, переходящими другие мосты, а также лабораторные исследования отдельных людей, пытающихся передвигаться, не теряя равновесия, по шатающейся опоре. Самое удивительное, однако, заключается в том, что спустя лишь два дня после закрытия моста Millenium Bridge и еще до начала каких-либо исследований, призванных установить причину неожиданного поведения этого моста, один из читателей лондонской газеты Guardian успел найти правильное объяснение. Четырнадцатого июня 2000 г. в редакцию газеты пришло следующее письмо.