Книга: Земля и космос. От реальности к гипотезе
Глава 8 Люксонная стена
| <<< Назад Глава 7 Человек, который «взмассил» Землю |
Вперед >>> Глава 9 Играя в игры |
Глава 8
Люксонная стена
Как вы думаете, мои научные очерки появлялись в «Тайм»? (Давайте зададим этот вопрос, почему бы нам его не задать? А между тем это так, статья, о которой идет речь, появилась несколько месяцев назад, она называлась «Невозможно, и это все».
А касается статья невозможности достижения скорости света и превышения этой скорости. После того как статья была опубликована, появилось очень много разговоров о частицах, которые двигались быстрее скорости света, и на их фоне я выглядел занудой, который не признает развития физики, преодолевшей рамки старого мышления. Что еще хуже, в ней цитировался мой старый друг Артур Кларк (упомянул об это лишь случайно. — Примеч. авт.), и его рассуждения имели заголовок «Возможно, это все», что создавало впечатление, будто Артур смотрит вперед намного дальше, чем я.
К счастью, я настолько терпим, что меня не волнуют подобные вещи, и я просто выбросил это из головы. Когда я в следующий раз встретил Артура, мы по-прежнему оставались друзьями — если не считать легкого удара в челюсть, который он получил от меня.
В любом случае я не зануда, и мне не нужно прилагать слишком много усилий, чтобы это доказать.
Давайте начнем с уравнения, которое впервые было выведено голландским физиком Хендриком Антоном Лоренцем в 1890-х годах. Лоренц думал, что уравнение применимо только к электрически заряженным телам, но Эйнштейн позднее ввел его в теорию относительности, показав, что оно применимо ко всем телам, вне зависимости от того, несут они электрический заряд или нет.
Я не буду представлять уравнение Лоренца в его обычной форме, а покажу несколько видоизмененным. Моя версия этого уравнения следующая:
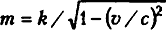
В этом уравнении m представляет массу тела, v — скорость, с которой тело движется относительно наблюдателя, с — скорость света в вакууме, a k — некоторое значение, постоянное для рассматриваемого тела.
Далее предположим, что тело движется с одной десятой скорости света. Это означает, что v = 0,1с. В этом случае дискриминатор дроби с правой части уравнения 1 становится:
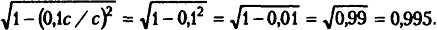
Уравнение 1, таким образом, после преобразования выглядит так:
m = k/0,995 = 1,005k.
Мы можем применить это же уравнение к разным, постепенно возрастающим скоростям, скажем, к скоростям 0,2с, 0,3с, 0,4с и так далее. Я не буду утомлять вас вычислениями и сразу представлю конечный результат:
Скорость / Масса
0,1с / 1,005k
0,2с / 1,03k
0,3с / 1,05k
0,4с / 1,09k
0,5с / 1,15k
0,6с / 1,24k
0,7с / 1,41k
0,8с / 1,67k
0,9с / 2,29k
Как видите, из уравнения Лоренца, если оно верно, должно следовать, что масса любого объекта постоянно возрастает при увеличении скорости. Когда было сделано впервые такое предположение, оно казалось противоречащим здравому смыслу, потому что подобного изменения массы до сих пор найти не удавалось.
Причина этого состоит в том, что значение с очень велико по земным меркам — 186 281 миль/с. Со скоростью одной десятой скорости света масса любого объекта возрастает на 0,5 % массы объекта, движущегося со скоростью 60 миль/ч — и это увеличение в принципе может быть определено. Однако скорость «всего» в одну десятую скорости света (0,1с) составляет целых 18 628 миль/с, или 67 миль/ч. Другими словами, чтобы произвести измерения массы, скорости должны быть такими, которые были еще неизвестны ученым 1890-х.
Однако всего через несколько лет были найдены субатомные частицы, вылетающие из радиоактивного атомного ядра со скоростью, очень близкой к скорости света. Их массы могли быть измерены довольно точно при различных скоростях, и уравнение Лоренца получило бы еще одно подтверждение своей верности. Но и до этого момента не было найдено ни одного нарушения уравнения Лоренца для любого тела, двигающегося с измеряемой скоростью.
Таким образом, мы должны принять уравнение Лоренца как верное представление описанной нами грани Вселенной — по крайней мере до следующего замечания.
Приняв уравнение Лоренца, зададим себе несколько вопросов. Первый: что представляет собой k?
Чтобы ответить на этот вопрос, рассмотрим какое-либо тело, имеющее массу, покоящимся относительно наблюдателя. В этом случае его скорость равна нулю, и поскольку v = 0, тогда v/c = 0 и (v/c)2 = 0. Более того,
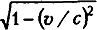
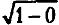
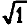
Это означает, что для какого-либо тела, покоящегося относительно наблюдателя, уравнение Лоренца приобретает вид m = k/1 = k. Из этого мы можем заключить, что k — это масса тела в покое относительно наблюдателя. Ее обычно называют массой покоя и обозначают m0. Уравнение Лоренца записывают следующим образом:
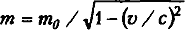
Следующий вопрос: что произойдет, если объект движется со скоростью большей, чем самая высокая скорость, представленная выше в таблице. Предположим, что объект движется со скоростью 1,0с относительно наблюдателя; другими словами, он движется со скоростью света.
В этом случае выражение под корнем уравнения Лоренца выглядит так:
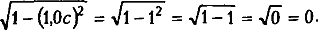
Это означает, что для тела, движущегося со скоростью света, уравнение Лоренца приобретает вид: m = m0/0, а из основ математики мы знаем, что делить на ноль нельзя. Математически уравнение Лоренца становится бессмысленным для тела, имеющего массу и движущегося со скоростью света.
Хорошо, тогда давайте возьмем другую скорость.
Пусть скорость из уравнения 2 будет больше 0,9с — при этом выражение под корнем начнет быстро приближаться к нулю, а значение m — стремительно возрастать. Это происходит независимо от значения m0. (Постарайтесь сами рассчитать m для значений скорости 0,99, 0,999 и 0,9999 и так далее, насколько у вас хватит терпения.)
На языке математики мы можем сказать, что в уравнении с = а/b (где а больше, чем 0) при приближении b к нулю с увеличивается беспредельно, то есть это можно записать так: а/0 = ?, где ? представляет собой неограниченное возрастание, или бесконечность.
Тогда мы можем сказать, что для любого объекта, имеющего массу (какой бы малой она ни была), эта масса приобретает бесконечные значения, когда его скорость приближается к скорости света относительно наблюдателя.
Это означает, что тело не может в действительности достичь скорости света (хотя оно может бесконечно стремиться к этому значению) и определенно не может ее превзойти. Вы можете аргументировать это следующим образом.
Единственный известный нам метод заставить какой-либо объект двигаться с большей величиной, чем скорость света, — это приложить к нему силу, которая бы произвела это ускорение (см. главу 6). Однако чем больше масса, тем меньше ускорение, произведенное данной силой, и, таким образом, когда масса приближается к бесконечным величинам, ускорение, каким бы большим поначалу оно ни было, будет стремиться к нулю. Следовательно, ни один объект не может двигаться быстрее, чем скорость, при которой масса становится бесконечной.
Второй аргумент таков. Движущееся тело имеет кинетическую энергию, которую мы можем считать равной mv2/2, где m — масса, a v — скорость. Если к телу прикладывается сила таким образом, что кинетическая энергия возрастает, эта энергия может увеличиться потому, что увеличивается v, или потому, что увеличивается m, или же из-за одновременного увеличения как v, так и m. При обычных скоростях все изменения происходят только со скоростью, так что мы можем предположить (хотя это предположение неверное), что масса остается постоянной при всех обстоятельствах.
Однако на самом деле как скорость, так и масса возрастают в результате приложения силы, но изменение массы столь незначительно при обычных скоростях, что измерения незаметны. Однако когда скорость относительно наблюдателя возрастает, то все больше энергии будет затрачиваться на увеличение массы и меньше — на возрастание скорости. Ко времени, когда скорость окажется очень близкой к скорости света, фактически вся энергия будет затрачиваться на увеличение массы, и ничего не будет оставаться на увеличение скорости. Это приведет к тому, что скорость света никогда не будет достигнута.
И не спрашивайте почему. Так устроен мир.
Однако я надеюсь, вы заметили, что, рассказывая о бесконечном возрастании массы при скорости света, я был вынужден утверждать: «Это правда независимо от значения m0 — важно лишь то, что оно отлично от нуля».
Конечно, все частицы, из которых мы состоим, — протоны, электроны, нейтроны, мезоны, гипероны и так далее, — имеют массу покоя больше нуля, так что эта оговорка не кажется очень ограничивающей. В самом деле, люди обычно говорят: «Невозможно достичь или превысить скорость света», не уточняя, что они имеют в виду объекты, имеющие массу покоя большую, чем ноль, поскольку они считают, что такими являются все объекты.
Я не уточнял это в статье «Невозможно, и это все», что и дало возможность посчитать меня занудой. Если мы примем во внимание это ограничение, тогда все, что я сказал, примет законченный вид.
А теперь продолжим и рассмотрим тела с массами m0, не отличными от нуля.
Возьмем, к примеру, фотон, частицу электромагнитного излучения — видимый свет, микроволны, гамма-лучи и так далее.
Что мы знаем о фотонах? В первую очередь то, что фотон всегда имеет конечную энергию, так что значение этой энергии находится где-то между 0 и ?. Энергия, как показал Эйнштейн, эквивалентна массе, согласно уравнению, которое он записал в следующем виде: e = mc2. Это означает, что масса любого фотона может быть вычислена при помощи этого уравнения и иметь величину от 0 и до ?.
Мы также знаем о фотонах, что они движутся (относительно любого наблюдателя) со скоростью света. В самом деле, свет имеет эту скорость потому, что он «состоит» из фотонов.
Теперь, когда нам известны эти две вещи, преобразуем уравнение 2:
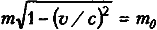
Для фотонов v = с, и теперь уравнение 3 приобретает вид:
m(0) = m0 (уравнение 4).
Если бы фотон был обыкновенным, имеющим массу объектом и перемещался бы со скоростью света, его масса (m) была бы бесконечной. Уравнение 4 тогда бы приобрело вид ? ? (0) = m0, а подобное уравнение в математике недопустимо.
Фотон, однако, может приобрести значение для m от 0 до ? (хотя он и перемещается со скоростью света), но для любого значения m между 0 и ? значение m0 в уравнении 4 равно 0.
Это означает, что для фотонов масса покоя (m0) равна нулю. Если масса покоя равна нулю, значит, объект может двигаться со скоростью света.
(Это дает ответ на вопрос, который постоянно мне задают корреспонденты, считая, что они нашли противоречие в логике Эйнштейна. Вопрос звучит так: «Если что-либо, двигающееся со скоростью света, имеет бесконечную массу, как могут фотоны не иметь бесконечную массу?» Ответ заключается в том, что следует различать частицы, чья масса покоя равна 0, и частицы, у которых масса покоя больше 0. К сожалению, корреспонденты будут задавать свой вопрос вне зависимости от того, как часто я буду им это объяснять.)
Но пойдем дальше. Предположим, что фотон движется со скоростью, меньшей скорости света. В этом случае величина под квадратным корнем в уравнении 3 станет больше нуля — и к тому же будет умножена на массу m, величина которой больше нуля. Если два значения, каждое из которых больше нуля, умножить, тогда результат (в данном случае m0) должен быть больше нуля.
Это означает, что, если фотон движется со скоростью, меньшей скорости света (не важно, насколько меньшей), его масса покоя не может быть равной нулю. То же самое будет справедливо по отношению к фотону, двигающемуся со скоростью, большей скорости света. (В дальнейшем мы увидим, что с уравнением на скоростях, больших скорости света, происходят довольно забавные вещи — но при всем этом следует помнить, что масса покоя в этом случае уже не может быть равна нулю.)
Физики настаивают на том, что масса покоя должна быть постоянной для любого данного тела, поскольку все феномены, которые они измеряют, имеют смысл только в этом случае. Для того чтобы масса покоя фотона оставалась постоянной, фотон всегда должен двигаться со скоростью света, и ни на йоту больше или меньше — конечно, при условии движения сквозь вакуум.
Когда фотон возникает, он немедленно, без какой-либо задержки во времени, начинает двигаться прочь из точки происхождения со скоростью 186 281 миль/с. Это может звучать парадоксально, поскольку подразумевает бесконечное ускорение и, таким образом, бесконечную силу — но стоп…
Второй закон Ньютона, связывающий силу, массу и ускорение, применим только к телам с массой покоя больше нуля. Он действительно неприменим к телам, чья масса покоя равна нулю.
Таким образом, если энергия вливается в обыкновенное тело при обыкновенных условиях, его скорость возрастает; если энергия вычитается, его скорость уменьшается. Если энергия вливается в фотон, его частота (и масса) увеличивается, но скорость остается неизменной; если энергия вычитается, его частота (и масса) уменьшается, но скорость также остается неизменной.
Но если все это так, то кажется лишенным здравого смысла говорить о «массе покоя» в связи с фотонами, поскольку это подразумевает, что фотон имеет в покое массу, а фотон никогда не может быть в покое.
Альтернативный термин был предложен О. М. Биланюком и И. К. Г. Сударшаном. Этот термин — «собственная масса». Собственная масса объекта — это постоянное значение массы, которая неотъемлемо свойственна телу и не зависит от скорости. В случае с обыкновенными телами эта свойственная телу масса равна той, которая может быть измерена у данного тела в состоянии покоя. Но в случае с фотоном таких прямых измерений сделать невозможно, и потому приходится определять его массу путем размышлений.
Фотон не единственное тело, которое может и должно двигаться со скоростью света. Любое тело с собственной массой, равной нулю, может и должно так вести себя. Вдобавок к фотонам существует не менее пяти различных видов частиц, у которых, как полагают, собственная масса равна нулю.
Одна из них — гипотетический гравитон — источник силы гравитации. Существование гравитона, похоже, в 1969 году было подтверждено окончательно.
Другие четыре частицы — это различные нейтрино: 1) само нейтрино, 2) антинейтрино, 3) мюон-нейтрино и 4) мюон-антинейтрино.
Гравитон и все нейтрино могут и должны передвигаться со скоростью света. О. М. Биланюком и И. К. Г. Сударшаном было высказано предложение, что все частицы, двигающиеся со скоростью света, должны быть объединены вместе в группу «люксонов» (от греческого слова, обозначающего «свет»).
Все частицы с собственной массой больше нуля, которые, таким образом, не могут достичь скорости света и потому должны всегда двигаться с меньшими скоростями, собраны вместе в класс «тардионов». Позднее появилось выражение «subluminal», «досветовые», для обозначения скоростей тардионов.
Но представим себе то, что невозможно представить, и рассмотрим частицы, которые могут двигаться со сверхсветовыми скоростями. Впервые в строгом соответствии с релятивистскими принципами (не как простое рассуждение в стиле научной фантастики) это предположение было рассмотрено Биланюком, Сударшаном и Дешпанде в 1962 году — и их работы оставались в центре внимания до того, как Жирар Файнберг в 1967 году опубликовал похожие рассуждения (именно работа Файнберга вызвала дискуссию в «Тайм»).
Предположим, что частица движется со скоростью 2с, то есть вдвое большей скорости света. В этом случае v/c станет 2с/с, или 2, а (v/c)2 будет 4. Выражение
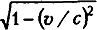
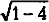
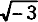
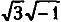
Поскольку
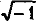
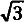
1,73mi = m0 (уравнение 5).
Выражение, которое содержит i (то есть
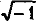
Легко видеть из взятых наугад примеров, что для любого предмета, двигающегося при сверхсветовых скоростях, собственной массой является мнимая величина.
Мнимая масса не имеет никакого физического значения в нашей «досветовой» вселенной, и потому долгое время было принято сразу просто отмахиваться от сверхсветовых скоростей, поскольку не может быть мнимой массы. Я сам это говорил в свое время.
Но на самом ли деле мнимая масса не имеет никакого значения? Или, может, произведение mi — это просто математическое выражение некоторого набора правил, к которому мы еще не привыкли, — но правил, которые все же подчиняются диктату специальной теории относительности Эйнштейна?
К примеру, мы знаем, что в баскетболе, американском футболе, футболе, хоккее и так далее победителем считается тот — или та команда, — кто имеет больше очков. Но разве это значит, что нет игр, где победитель имеет меньше очков? К примеру, гольф? Главное в любой игре — мастерство; выигрывает тот, кто справляется с более трудными задачами; если о мастерстве, как правило, говорит больший счет, то в гольфе — меньший.
Для того чтобы соблюдались правила специальной теории относительности, любой объект с «мнимой» массой покоя должен вести себя таким образом, который кажется парадоксальным тем, кто привык иметь дело с объектами с реальной массой покоя.
В этом случае если какой-нибудь объект с мнимой массой покоя увеличивает свою энергию, его скорость уменьшается, если уменьшает энергию, то его масса увеличивается. Другими словами, любой объект с мнимой массой покоя замедляется, когда к нему прикладывается сила, и ускоряется, когда встречает сопротивление.
Более того, когда такие частицы получают энергию и замедляются, они никогда не могут замедлиться до скорости света. Близ скорости света их скорость становится бесконечной. Однако когда их энергия уменьшается до нуля, их скорость возрастает беспредельно. Любое тело с мнимой массой покоя, которое имеет нулевую энергию, будет иметь неограниченную скорость. Такие частицы всегда движутся быстрее света, и Файнберг предложил называть их «тахионами» (от греческого слова, означающего «быстрый»).
Хорошо, тогда вселенная из тардионов состоит из частиц, движущихся со скоростями, меньшими скорости света. Вселенная из тахионов состоит из частиц, что движутся быстрее скорости света — от с для бесконечной энергии до ? для нулевой энергии. Между этими двумя вселенными находится люксонная вселенная, со скоростями с — не больше и не меньше при любой энергии.
Мы видим, что вся Вселенная как бы разделена на два отделения непроницаемой стеной. С одной стороны — тардионная вселенная, с другой — тахионная, а между ними бесконечно тонкая, но очень жесткая люксонная стена.
В тардионной вселенной большинство объектов имеют малую кинетическую энергию. Те объекты, которые имеют большие скорости (такие, как космические частицы), обладают очень малой массой. Объекты с большими массами (такие, как у звезды) имеют очень маленькую скорость.
То же самое, похоже, справедливо и по отношению к тахионной вселенной. Объекты с относительно малыми скоростями (всего немного большими скорости света) и, таким образом, обладающие большими энергиями, должны иметь малую массу и не очень отличаться от частиц космических лучей. Объекты с большими массами имеют малую кинетическую энергию и, таким образом, очень большие скорости. Звезда из тахионов, к примеру, должна передвигаться со скоростями, в триллионы раз превышающими скорость света. Но это означает, что масса звезды будет распределена по большим пространствам на протяжении очень малого времени, так что очень малая ее часть будет представлена в любом месте в данный промежуток времени.
Обе вселенные могут встретиться и стать различимыми только в одном месте — у люксонной стены (обе вселенные имеют в своем составе протоны, нейтроны и гравитоны).
Если у тахионов достаточно энергии, они двигаются медленно; может оказаться так, что энергии у них столь много, а движутся они в одном месте столь долго, что могут произвести распознаваемый выброс фотонов. Ученые ищут эти выбросы, но вероятность того, что прибор окажется в нужном месте, когда этот выброс (по всей вероятности, не частый) произойдет, судя по всему, равен одной миллиардной, если не еще меньше.
Конечно, у нас может возникнуть мысль: может, нет вообще возможности пробить люксонную стену каким-то другим путем, чем ускоряясь около нее? Но это невозможно. Могут ли тардионы как-то превратиться в тахионы (возможно, при помощи фотонов), столкнуться с фотонами, так чтобы одна из частиц внезапно оказалась по другую сторону стены, не проходя сквозь нее? (Точно так, как можно объединять тардионы для получения фотонов и внезапно получать объекты, которые движутся со скоростью света без чьего-либо ускорения.)
Преобразование в тахионы было бы равнозначно переходу в «гиперпространство», концепция которого очень мила писателям научной фантастики. В тахионной вселенной космический корабль с энергией, необходимой для движения на скорости, много меньшей скорости света, внезапно обнаружит, что он, затрачивая все ту же самую энергию, летит на скорости, во много раз большей скорости света. Он сможет добраться до отдаленной галактики, скажем, в три секунды, затем перейти обратно в тардионный вид и снова появиться в нашей вселенной. Это дало бы возможность «перепрыгнуть» к звездам, о чем я всегда говорю в своих повестях.
Однако в связи с этим у меня есть идея, которая для меня является совершенно новой. Она не основывается на каком-либо законе физики — я нашел ее чисто интуитивно. Она возникла только потому, что я убежден, что первостепенной характеристикой вселенной является ее симметрия и что первостепенным принципом является мерзкая доктрина: «Ты не можешь победить!»
Думаю, что каждая вселенная представляется себе тардионной вселенной, а на другие смотрит как на тахионную, так что наблюдателю из «ниоткуда» (к примеру, сидящему на вершине люксонной стены) покажется, что люксонная стена разделяет мир на две одинаковые части.
Если нам удастся перенести космический корабль в тахионную вселенную, мы обнаружим себя (я интуитивно это чувствую) все еще двигающимися, по нашим приборам, на досветовых скоростях, а вселенную, которую мы покинули, мы будем считать сверхсветовой.
И если это так, то, куда бы мы ни отправились, что бы мы ни использовали, тахионы или что-то еще, достижение скорости света и переход через нее останется невозможным — вот и все.
| <<< Назад Глава 7 Человек, который «взмассил» Землю |
Вперед >>> Глава 9 Играя в игры |
- Глава 8 Люксонная стена
- Межклеточное вещество
- 04. На что влияет нагрев планет звездами, звезд Ядрами Галактик, Ядер Галактик Ядрами Сверхгалактик
- Список литературы
- Разные человечества
- Красные тучи, закрывающие солнце
- Московская белая
- Муравей, семья, колония
- Примерные рационы для котят от месяца до пяти и старше
- Голосеменные растения завоевывают мир
- Пароль скрещенных антенн
- Позор страны
