Книга: О времени, пространстве и других вещах

Глава 7 Давайте побродим… посмотрим…

Глава 7

Давайте побродим… посмотрим…

В книгах по астрономии (а я их видел, поверьте, немало) обязательно содержится таблица, где перечислены планеты Солнечной системы с указанием диаметра, расстояния от Солнца, времени оборота, альбедо, плотности, числа спутников и т. д.

Я очень люблю числа и отношусь к ним с большим уважением, поэтому всегда с жадностью набрасываюсь на такие таблицы в надежде обнаружить новую информацию. И иногда получаю награду в виде данных о температуре на поверхности, орбитальной скорости и т. д. Однако информации всегда оказывается мало.

Поэтому всякий раз, когда мой мозг начинает настойчиво требовать очередную порцию пищи для размышлений, я даю ему информацию, которой в данный момент располагаю, затем посвящая долгие часы досуга выводам, предположениям и формулировке всевозможных гипотез. (По крайней мере, я занимался этим в те далекие времена, когда еще имел досуг.)

В общем, я и теперь этим занимаюсь, только облекаю результаты своих размышлений в форму очерков и статей. Если хотите, присоединяйтесь ко мне: мы вместе побродим, оглядимся по сторонам и посмотрим, что получится.

Давайте начнем так…

Если верить Ньютону, каждый объект во Вселенной притягивает другой объект с силой (f), пропорциональной произведению масс этих объектов (m₁ и m₂), деленной на квадрат расстояния между их центрами (d). Чтобы получить равенство, умножаем результат на гравитационную постоянную (g).

Это означает, что существует притяжение между Землей и Солнцем, между Землей и Луной, а также между Землей и всеми планетами, спутниками, метеоритами и каждой песчинкой космической пыли во Вселенной.

К счастью, Солнце так огромно по сравнению со всеми остальными объектами Солнечной системы, что при расчете орбиты Земли или любой другой планеты делается допущение (если рассматриваются только Солнце и конкретная планета), что они одни во Вселенной. Влияние остальных небесных тел может быть подсчитано позже.

Так же можно рассчитать орбиту спутника, предположив, что он и его основная планета одни во Вселенной.

Здесь есть кое-что, на мой взгляд, чрезвычайно интересное. Если Солнце многократно массивнее любой планеты, разве оно не должно оказывать влияние и на спутники, даже находясь на значительно большем расстоянии, чем его родная планета? Если так, каким образом можно оценить это влияние?

Представим себе этот процесс в виде перетягивания каната, на одном конце которого находится спутник со своей планетой, а на другом — Солнце. Как поведет себя Солнце в этом соревновании?

Думаю, что астрономы все это давно подсчитали, однако я ни разу не видел результатов этих расчетов в литературе, поэтому решил выполнить их сам.

Вот что можно сделать. Давайте обозначим массу спутника m, массу его планеты (вокруг которой он вращается) m_р, массу Солнца — ms. Расстояние от спутника до планеты у нас будет d_р, а расстояние от спутника до Солнца — ds. Гравитационная сила, действующая между спутником и планетой, — fp, а между спутником и Солнцем — fs. Вот и все. Обещаю, больше вы не увидите никаких новых обозначений, по крайней мере в этой главе.

Из формулы 1 видно, что сила притяжения между спутником и планетой:

а между тем же спутником и Солнцем:

Нам интересно узнать, насколько гравитационная сила, действующая между спутником и планетой, сравнима с аналогичной силой, действующей между спутником и Солнцем. Иными словами, чрезвычайно любопытно вычислить отношение fp/fs, которое можно назвать «коэффициентом перетягивания каната». Чтобы его получить, следует разделить формулу 2 на формулу 3. Результат приведен в формуле 4:

При делении формула несколько упростилась. Во-первых, исчезла гравитационная постоянная, и нам не придется иметь дело с малыми числами и неудобными размерностями. С другой стороны, сократилась масса спутника (иными словами, для получения «коэффициента перетянутого каната» не имеет значения размер спутника).

В формуле остались отношение массы планеты к массе Солнца, а также квадрат отношения расстояния от спутника до Солнца к расстоянию от спутника до планеты.

Спутники имеют только шесть планет. Это Нептун, Уран, Сатурн, Юпитер, Марс и Земля (в порядке убывания расстояния от Солнца).

Произведя подсчет отношения масс, получим следующие результаты:

Как видите, отношение масс явно в пользу Солнца. Даже Юпитер — самая тяжелая из планет — не дотянул до ¹/₁₀₀₀ массы Солнца. В действительности суммарная масса всех планет (с учетом спутников, астероидов, комет и метеоритов) составляет не более ¹/₇₅₀ массы Солнца.

Пока у Солнца имеются все шансы выиграть соревнования по перетягиванию каната.

Однако нам следует рассмотреть и отношение расстояний, а здесь все говорит в пользу планеты, потому что любой спутник располагается ближе к своей родной планете, чем к Солнцу. Тем более, что это отношение расстояний следует еще возвести в квадрат. После этого уже можно почти не сомневаться, что Солнце не перетянет канат. Но все-таки проверим.

Начнем с Нептуна. Он имеет два спутника — Тритон и Нереиду. Среднее расстояние каждого из них от Солнца примерно такое же, как среднее расстояние Нептуна от Солнца, — 2 797 000 000 миль. Среднее расстояние Тритона от Нептуна — 220 000 миль, а среднее расстояние Нереиды от Нептуна — 3 460 000 миль.

Разделив расстояние от Солнца на расстояние от Нептуна до каждого спутника и возведя результат в квадрат, получим 162 000 000 для Тритона и 655 000 для Нереиды. Умножив каждое из этих чисел на отношение масс Нептуна и Солнца, получим следующие коэффициенты:

Таким образом, условия, в которых существуют спутники, очень различны. Гравитационное влияние Нептуна на свой ближайший спутник — Тритон — намного больше, чем влияние на него Солнца. Нептун схватил Тритон весьма уверенно. Притяжение Нептуном своего внешнего спутника — Нереиды — является значительным, но не подавляющим по сравнению с Солнцем. К тому же Нереида имеет эксцентричную орбиту, и более эксцентричной орбиты нет ни у одного спутника в Солнечной системе. В одном ее конце Нереида приближается к Нептуну на 800 000 миль, в другом удаляется более чем на 6 000 000 миль. В точке наибольшего удаления от планеты «коэффициент перетягиваемого каната» имеет необыкновенно низкую величину — всего лишь 11!

По многим причинам (одной из которых является эксцентричность ее орбиты) астрономы обычно считают, что Нереида является не настоящим спутником Нептуна, а малой планетой, случайно попавшей в его гравитационное поле.

То, что Нептун так слабо держит Нереиду, казалось бы, подтверждает это. Действительно, объединение Нептуна и Нереиды вполне может быть временным явлением. Возможно, что эффект солнечного тяготения когда-нибудь вырвет спутник из объятий Нептуна. Зато Тритон никогда не покинет своего отца, конечно, если не произойдет катастрофы вселенского масштаба.

Я не стану приводить в этой книге подробные вычисления для всех спутников Солнечной системы. Поверьте, что я их выполнил, и теперь кратко познакомлю вас с основными результатами. Уран, например, имеет пять спутников, все они вращаются в плоскости экватора планеты, и астрономы не сомневаются, что все пять — настоящие спутники. Это Миранда, Ариель, Умбриель, Титания и Оберон.

«Коэффициенты перетягиваемого каната» для этих спутников следующие:

Другими словами, все они находятся в крепких объятиях Урана.

Теперь мы перейдем к Сатурну, имеющему девять спутников: Мимас, Энселад, Тефия, Диона, Рея, Титан, Гиперион, Япет и Феба. Восемь из них, расположенные ближе к планете, вращаются в плоскости экватора Сатурна и считаются его настоящими спутниками. Девятый, Феба, имеет наклонную орбиту и, судя по всему, является захваченным гравитационным полем астероидом.

«Коэффициент перетягиваемого каната» для этих спутников следующий:

Обратите внимание на низкое значение коэффициента для Фебы.

Юпитер имеет двенадцать спутников. Я рассмотрю их в два этапа. Первые пять — Амалфея, Ио, Европа, Ганимед и Каллисто — вращаются в плоскости экватора планеты и считаются настоящими спутниками. Искомый коэффициент для них:

Иными словами, Юпитер держит их крепко.

Однако у планеты имеется еще семь спутников, не имеющих официальных названий (см. главу 5), которые известны под номерами, обозначенными римскими цифрами (от VI до XII). Они присваивались по мере их открытия. Если расположить эти спутники в порядке возрастания расстояния от планеты, получится следующий ряд: VI, X, VII, XII, XI, VIII, IX. Все они малы, имеют эксцентрические орбиты и вращаются в плоскостях, наклоненных под разными углами к плоскости экватора Юпитера. Астрономы считают их захваченными астероидами. (Юпитер намного больше других планет и располагается ближе к поясу астероидов, поэтому вряд ли стоит удивляться, что он сумел захватить семь из них.)

Последнее подтверждает и низкое значение рассматриваемого коэффициента.

Юпитер явно не стремится удержать свои внешние спутники во что бы то ни стало.

У Марса два спутника — Фобос и Деймос оба имеют небольшие размеры и располагаются очень близко к планете. Они вращаются в плоскости марсианского экватора и являются настоящими спутниками. «Коэффициент каната» для них имеет следующие значения:

Таким образом я выполнил расчеты для 30 спутников, из которых 21 считается настоящим, а 9 рассматриваются как захваченные астероиды. Я пока ничего не говорю о 31-м спутнике, которым является наша Луна, но обязательно вернусь к этому вопросу. Подведем итоги.

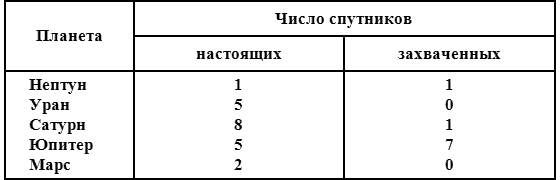
Маловероятно, что будут еще обнаружены настоящие спутники (хотя кто знает: Миранда была открыта в 1948 году), но что касается захваченных астероидов, они могут появляться в неограниченном количестве.

Давайте проанализируем величины «коэффициента каната» спутников. Среди настоящих спутников наиболее низок он у Деймоса — 32. С другой стороны, среди девяти спутников, считающихся захваченными астероидами, самый высокий коэффициент у Нереиды — 34.

Будем считать цифру 30 минимальным значением для настоящего спутника. Тогда все спутники, имеющие меньшие значения коэффициента, вероятнее всего, являются захваченными астероидами и могут быть временными членами семьи планет.

Зная массу планеты и ее расстояние от Солнца, можно подсчитать расстояние от центра планеты, на котором будет действовать этот коэффициент. Для этой цели воспользуемся формулой 4, приняв отношение fp/fs равным 30. Подставив известные величины mp, ms и ds, вычислим dp. Получим максимальное расстояние, на котором можно обнаружить настоящий спутник. Единственная планета, для которой нельзя выполнить такие вычисления, — Плутон, масса которой не определена. Ну и что? Пропустим Плутон!

Также мы можем установить минимальное расстояние, на котором еще можно обнаружить настоящий спутник. Доказано, что если спутник подойдет к планете ближе некоторого минимального расстояния, то не сохранит устойчивость на орбите. Это расстояние называется «пределом Роша» по имени французского астронома Э. Роша, подсчитавшего его в 1849 году. Предел Роша — это расстояние от центра планеты, равное 2,44 ее радиуса.

Я выполнил расчеты для четырех внешних планет и свел результаты в таблицу.

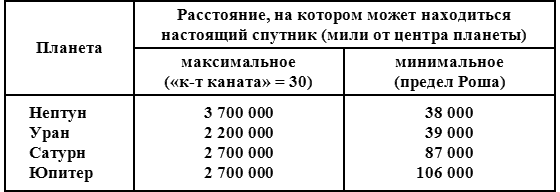
Как видите, каждая из этих планет, имеющих большую массу и расположенных на значительном удалении от Солнца, имеет достаточно свободного пространства для сложной системы спутников. Поэтому на эти четыре планеты и приходится подавляющее большинство спутников — 21.

Сатурн удерживает около себя кольцевую систему, которая нарушает границу предела Роша. Край кольцевой системы находится в 85 000 миль от центра планеты. Очевидно, вещество колец вполне могло стать спутником, если бы не находилось так близко к планете.

Мы видим только планеты нашей Солнечной системы. В связи со спутниками есть смысл говорить только о четырех самых крупных планетах.

Из них Сатурн имеет систему колец, а Юпитер ею едва не обзавелся. Самый близкий к планете спутник, Амалфея, расположен в 110 000 милях от ее центра, а предел Роша составляет 106 000 миль. Всего несколько тысяч миль — и у Юпитера тоже появились бы кольца. Мне представляется, что когда мы начнем изучать другие звездные системы, то непременно обнаружим, что больше половины больших планет будут обладать кольцами, как Сатурн.

Теперь давайте попробуем выполнить аналогичные расчеты для внутренних планет. Поскольку все они обладают гораздо меньшими габаритами и расположены намного ближе к Солнцу — своему основному сопернику, можно предположить, что диапазон расстояний, доступных для движения спутников, будет более ограниченным. И это действительно так и есть. Я выполнил соответствующие расчеты и свел их в таблицу.

Таким образом, вы можете сами убедиться, что если вокруг внешних планет спутники могут вращаться в диапазоне двух миллионов миль и больше, то у внутренних планет пространство для них куда более ограниченно. Марс и Венера приберегли для них лишь по 10 000 миль, у Земли спутники могут чувствовать себя более вольготно: на расстоянии до 20 000 миль.

Меркурий представляется наиболее интересным случаем. Максимальное расстояние, на котором может оказаться естественный спутник, в условиях неравного состязания с находящимся поблизости с Солнцем, уже попадает в границы предела Роша. Из этого следует, что Меркурий не может иметь естественных спутников.

Эта планета действительно не имеет спутников, но, насколько я знаю, никто это не потрудился объяснить. Этот факт принимается как эмпирический. Если кто-то из моих великодушных читателей, обладающих более обширными знаниями в области астрономии, укажет на мои ошибки, я отнесусь к этому с философским смирением. В конце концов, я не профессионал и занимаюсь исследованиями и расчетами ради собственного удовольствия.

У Венеры, Земли и Марса все-таки есть немного места для спутников. Правда, его очень мало и шансы собрать достаточно вещества даже для маленького спутника невелики.

Так случилось, что ни у Венеры, ни у Земли в обозначенных границах спутников нет, а у Марса их два, но оба имеют такие маленькие размеры (один в диаметре 12 миль, другой — 6), что их и спутниками можно назвать с большой натяжкой.

С чувством глубокого удовлетворения могу отметить, что все мои соображения, приведенные выше, блестяще подтверждаются на практике существующими спутниковыми системами различных планет. И мне немного стыдно, что до сей поры я обходил молчанием одну небольшую деталь, можно сказать, крошечный пустячок…

Какое место в выстроенной мной стройной, изящной системе занимает наша Луна?

Если следовать моим выводам, — а мне они очень нравятся, чтобы легко от них отказаться, — она слишком далеко от Земли, чтобы быть ее настоящим спутником. Но она слишком велика, чтобы быть захваченной гравитационным полем Земли. Шансы на это представляются ничтожными.

Существуют теории, что когда-то Луна находилась намного ближе к Земле (в границах, отведенных мною для настоящих спутников), но постепенно удалилась. У меня на это есть возражение. Если Луна когда-то была настоящим спутником, первоначально кружившим вокруг Земли на расстоянии, к примеру, 20 000 миль, она почти наверняка вращалась бы в плоскости земного экватора. Однако она этого не делает!

Тогда возникает закономерный вопрос: если Луна не является ни настоящим спутником, ни захваченным, что же это такое? Вероятно, вы удивитесь, но ответ у меня есть. Для наглядности давайте вернемся к моим вычислениям «коэффициента перетягивания каната». Для одного спутника я этот коэффициент не вычислил. Давайте сделаем это сейчас.

Среднее расстояние от Земли до Луны — 237 000 миль, а среднее расстояние от Луны до Солнца — 93 000 000 миль. Отношение расстояний — 392. Если это число возвести в квадрат, получится 154 000. Отношение массы Земли к массе Солнца было приведено ранее в этой главе и составляет 0,0000030. Умножив это число на 154 000, получим искомый коэффициент — 0,46.

Иными словами, Луна занимает среди остальных спутников Солнечной системы совершенно особое положение. Она уникальна тем, что ее родная планета — Земля — проиграла соревнование с Солнцем по «перетягиванию каната». Солнце притягивает Луну в два раза сильнее, чем Земля.

Таким образом, мы можем рассматривать Луну не как настоящий или захваченный в гравитационное поле спутник, а как самостоятельную планету, которая движется вокруг Солнца «в ногу» с Землей. Если вы изобразите в масштабе орбиты Земли и Луны вокруг Солнца, то увидите, что лунная орбита постоянно вогнута в сторону Солнца. Она всегда «падает» к Солнцу. Все остальные спутники, причем без единого исключения, «падают» в противоположную сторону.

Не забывайте, что Луна вращается вокруг Земли вовсе не в плоскости земного экватора, как этого следовало ожидать от спутника. Плоскость ее орбиты подходит достаточно близко к эклиптике, то есть к плоскости, в которой планеты обычно вращаются вокруг Солнца. Именно так и должна вести себя планета!

Представляется возможным, что существует некое промежуточное состояние между тяжелой планетой, расположенной далеко от Солнца и представляющей собой ядро с многочисленными спутниками вокруг, и маленькой планетой недалеко от Солнца, которая также является ядром но уже без спутников. Разве не могут создаться условия, при которых произойдет сгущение вещества, и из двух ядер образуется, так сказать, двойная планета?

Возможно, Земля лишь подошла к границе допустимой массы и расстояния, она оказалась немного меньше и чуть ближе, чем нужно. Быть может, если бы мы были немного иначе расположены, две половинки двойной планеты оказались бы больше похожи? На обеих могла быть атмосфера, океаны, а главное — жизнь. Нельзя исключить, что в иных звездных системах двойные планеты — обычное дело.

Как стыдно, если мы прозевали такое…

А быть может (кто знает), какое счастье!