Книга: О времени, пространстве и других вещах

Глава 12 Ничего считается

<<< Назад Глава 11 Забудьте об этом!

Вперед >>> Глава 13 Буквой с обозначается скорость света в пустоте

Глава 12

Ничего считается

В предыдущей главе я говорил о разных вещах, в том числе о римских числительных. Процесс их устаревания длился пять веков, однако даже сейчас они представляют определенный интерес для пытливого, ищущего ума.

По-моему, это происходит оттого, что они добавляют знающему их человеку некую толику самоуважения. Идет, к примеру, некто мимо столба, на котором написано: «Возведен в MCMXVIII». «Ах вот как, — восклицает сей образованный индивид, значит, его построили в 1918 году!» И получает повод проникнуться уважением к самому себе.

Понятие о числах и действиях с ними возникло еще в доисторические времена. Думаю, сейчас на нашей планете уже не осталось племен, даже находящихся на примитивном уровне развития, которые не имели бы представления о числах.

После возникновения письменности — а именно это событие находится на границе между «доисторическими временами» и древностью — возникла необходимость сделать следующий шаг — записать числа. Конечно, совсем не трудно записать числа при помощи букв как любое слово. В английском языке число пальцев на одной руке выражается словом «five» (пять), а на всех четырех конечностях словом «twenty» (двадцать).

Еще в далекой древности королевские сборщики налогов, летописцы, переписчики заметили, что числа — это не простые слова, они располагаются в строго определенном порядке. Поэтому следовало придумать для их обозначения особые знаки.

Если, к примеру, обозначить число 1 — ?, 2 — ??, 3 — ??? и т. д., весь ряд может быть выражен символически без особого труда. Легко можно убедиться, что символ ??????????????????????? обозначает 23. Более того, этот символ универсален и обозначает 23 на любом языке.

Однако прочитать слишком много значков в непрерывном ряду не всегда легко. Поэтому представляется логичным разбить такой ряд на небольшие группы. Поскольку мы привыкли для подсчета пользоваться пальцами руки, вполне можно разбить ряд знаков на группы по пять единиц. Тогда число 23 будет выглядеть следующим образом: ????? ????? ????? ????? ???. Если мы уже находимся на более высоком уровне развития и можем использовать для счета пальцы обеих рук, то же самое можно выразить так: ?????????? ?????????? ???. Если привлечь к работе и пальцы ног, можно разбивать значки в группы по двадцать.

Эти три метода разбивки ряда символов на более мелкие группы, с которыми легче обращаться, оставили свой след во всех числовых системах, которыми пользуется человечество. Наибольшее распространение получила разбивка на группы по 10. Двадцать символов в одной группе — очень много для восприятия, а пять — с увеличением числа получается слишком много групп. Таким образом, десять — удачный компромисс.

Следующий логичный шаг — обозначить группу из 10 символов особым знаком. Нет никакого резона всякий раз выписывать ??????????, если вместо этого можно использовать всего один значок, к примеру ?. В таком случае 23 будет записано следующим образом: ? ? ???.

Если вы начали двигаться в этом направлении, следующие шаги совершенно очевидны. С течением времени десять групп по десять (100) обозначаются другим знаком, например +. 10 сотен (тысячи) станут = и т. д. Тогда число 4675 может быть записано следующим образом:

= = = = + + + + + + ? ? ? ? ? ? ? ?????

Или так (для облегчения зрительного восприятия):

= = + + + ? ? ? ???.

?

= = + + + ? ? ? ??.

Между прочим, древние вавилоняне применяли именно такую систему, используя для этого клинопись.

Греки на ранних этапах развития тоже использовали подобную систему, но позже более популярным стал другой метод — с использованием букв алфавита.

Представляется естественным соотнести алфавит и числовой ряд. На первый взгляд они созданы именно для этого! Ряд «А, В, С, D, E…» идет так же гладко и стройно, как «1, 2, 3, 4, 5…»; кажется легким заменить один другим. Если мы используем недифференцированные символы, такие, как ??????? для «семи», все компоненты символа идентичны и должны быть записаны без исключения, если символ предназначен для обозначения числа 7, и ничего другого. С другой стороны, если «ABCDEFG» тоже обозначает 7 (посчитайте буквы и убедитесь), тогда, поскольку все символы различны, записать следует только последний. G — седьмая буква алфавита и обозначает цифру 7. Запомнить несложно. В этом случае работу символа, состоящего из семи компонентов, выполняет однокомпонентный символ. Кроме того, ?????? (шесть) на первый взгляд очень похоже на ??????? (семь), а буквы F (шесть) и G (семь) совершенно не похожи.

Греки, как вы понимаете, использовали свой алфавит. Но я для наглядности буду пользоваться нашими, значительно более знакомыми буквами. А = 1, В = 2, С = 3, D = 4, E = 5, F = 6, G = 7, H = 8, I = 9, J = 10.

Можно пойти далее и сказать, что K = 11, но тогда нашего алфавита хватит только на 26 цифр. Греки сделали лучше. Они воспользовались методом вавилонян разбивки на группы по десять. Если J = 10, это означает не только 10 предметов, но также одну группу из 10 предметов. Тогда можно использовать следующие буквы для обозначения десятков.

Иначе говоря, J = 10, K = 20, L = 30, M = 40, N = 50, O = 60, P = 70, Q = 80, R = 90. Далее можно продолжать с сотнями: S = 100, T = 200, U = 300, V = 400, W = 500, X = 600, Y = 700, Z = 800. Конечно, удобнее было бы продолжать до 900, но закончились буквы. Однако в старомодных алфавитах в конце иногда ставили значок &, поэтому мы имеем право довести дело до логического завершения и обозначить & = 900.

Таким образом, первые девять букв представляют собой единицы от 1 до 9, вторые — десятки, также от 1 до 9, третьи — сотни, и тоже от одной до девяти. (Раньше в греческом алфавите были только 24 буквы, а требовалось 27, поэтому для обозначения всех цифр греки добавили три устаревшие буквы.)

Такая система имела как преимущества, так и недостатки в сравнении с вавилонской системой. Основное преимущество заключалось в том, что любое число до 1000 выражалось тремя символами. К примеру, в соответствии с только что описанной мною системой 675 = XPE, а 816 = ZJF.

Ее существенный недостаток заключается в том, что для изображения чисел до 1000 следует запомнить и никогда не путать все 27 символов, а вавилоняне использовали для этого всего три символа.

К тому же греческая система прекращала свое действие, когда заканчивались буквы алфавита. Самое большое число, которое можно записать таким образом, — 999 = &RI. Далее необходимо вводить новые обозначения для групп тысяч, десятков тысяч и т. д.

Недостатком греческой системы являлось то, что одни и те же символы использовались для обозначения слов и чисел. Вполне можно что-то и перепутать. Между прочим, в греко-римские времена евреи приняли греческую систему представления цифр, но с использованием иудейского алфавита и сразу столкнулись с немалыми трудностями. Число 15 они записывали как «десять-пять». Но это же самое слово «десять-пять» у иудеев являлось именем Господа, которое нельзя было произносить всуе. Поэтому иудеям, чтобы не богохульствовать, пришлось ввести вместо «десять-пять» «девять-шесть».

Хуже того, слова в греко-иудейской системе выглядели как цифры. Например, используя наш алфавит, буквами WRA обозначается число 591. В алфавитной системе обычно все равно, в каком порядке располагать символы (хотя, как мы убедимся, это неприменимо к римским цифрам, которые также являются алфавитными), и WAR также означает 591. Согласитесь, легко поверить, что в этом числе есть что-то угрожающее, даже смертельно опасное.

Иудеи, самым внимательным образом изучавшие каждый слог в Библии, стараясь воспроизвести каждое Божье слово с максимальной точностью и должным почтением, умудрялись видеть числа во всех словах. Этим объясняется возникновение во времена Нового Завета целой мистической системы, которая строится на взаимосвязи слов и чисел в Библии. Именно тогда иудеи вплотную приблизились к математике. Они назвали свою систему gematria, что является искажением греческого geometria. Мы называем это науку нумерологией.

Даже в наше время кое-кто присваивает числовые обозначения буквам и таким образом решает, какие имена являются счастливыми, а какие — нет; кто на ком должен жениться и т. д. У меня такие псевдонаучные старания вызывают только улыбку.

Часть gematria нашла отражение и в более поздней истории. Я имею в виду последнюю книгу Нового Завета «Откровение Иоанна Богослова», написанную в мистической манере и представляющую сложность для литературного понимания. Мне кажется, что причина отсутствия ясности вполне очевидна. Автор «Откровения» разоблачает римское правительство и поэтому справедливо опасается гонений, если его произведение будет очевидным. Поэтому он предпринял попытку писать так, чтобы его поняла та часть читателей, к которой он обращался, а для римских властей его труд остался бы бессмыслицей.

В 13-й главе он повествует о «звере с семью головами и девятью рогами», а в 18-м стихе утверждает: «Здесь мудрость. Кто имеет ум, тот сочти число зверя, ибо это число человеческое; число его шестьсот шестьдесят шесть».

Совершенно очевидно, что автор не собирался таким образом придать святость псевдонауке gematria. Он имел в виду вполне конкретную личность. Насколько известно, «Откровение» было написано вскоре после первых гонений на христиан под предводительством Нерона. Если имя Нерона (Нерон Цезарь) записать в принятой у иудеев системе, то цифры, представленные буквами, действительно составляют 666 — «число зверя».

Разумеется, возможны и другие толкования. Если рассматривать «Откровение» как труд, имеющий значение не только для эпохи, когда он был написан, но и для грядущих времен, все сказанное может относиться и к некоему антихристу будущего. По этой причине многие поколения людей делали попытки (и продолжают этим заниматься) показать, что, если написать на определенном языке имя, а затем присвоить буквам цифровые обозначения, после чего произвести некоторые манипуляции и подсчитать сумму, можно получить «число зверя».

Христиане применяли это правило к Нерону; иудеи веком позже могли сделать то же самое по отношению к Гадриану. Спустя пять веков то же правило было применено к Мохаммеду. Во времена Реформации католики подсчитали, что «число зверя» дает имя Мартина Лютера, а протестанты, чтобы не остаться в долгу, быстро пришли к этому выводу в отношении сразу нескольких пап.

Несколько позже, когда религиозные столкновения сменились межнациональными, оказалось, что носителями «числа зверя» являются Наполеон Бонапарт и Вильгельм II. Более того, мне потребовалось всего несколько минут работы с собственной алфавитно-цифровой системой, чтобы показать: «Herr Adolif Hitler» также имеет число зверя. (Для этого потребовалось всего-навсего добавить дополнительное «і» в имя.)

Римская система цифровых символов имеет ряд сходств как с греческой, так и с вавилонской системой. Римляне, как и греки, использовали для обозначения цифр буквы алфавита. Однако они взяли не все буквы по порядку, а только несколько, повторяя их по мере необходимости, как и вавилоняне. Однако, в отличие от жителей Древнего Вавилона, римляне использовали новый символ не для каждого десятка, а для пятерки (что, естественно, более примитивно).

Итак, начнем: символ для цифры 1 — I, 2 = II, 3 = III, 4 = ІІІІ. 5 — это уже не ІІІІІ, а V. На протяжении веков ученые (и не только) развлекались, пытаясь придумать причину, по которой были выбраны конкретные буквы для обозначения цифр, но так и не сумели это сделать. Скорее всего, такой причины попросту не существует. Выбор, очевидно, был случайным, и буквы могли быть другими. Принято думать, что I символизирует вытянутый палец, а V — ладонь, где одна ветвь буквы — большой палец, а вторая все остальные пальцы. 6 = VI, 7 = VII, 8 = VIII, 9 = VIIII.

10 = X. Принято считать, что это символ скрещенных рук. 23 = XXIII, 47 = XXXXVII и т. д.

Для 50 был принят символ L, для 100 — С, для 500 — D, 1000 = M. Причем C и M запоминаются просто. C — первая буква слова centum (сто), а M — первая буква слова mille (тысяча). Последнее вызывает обоснованные подозрения. Являясь первыми буквами соответствующих слов, они могли вытеснить первоначально принятые для их обозначения символы. К примеру, альтернативным символом для 1000 мог быть символ (I), для 500 — правая половина этого знака, впоследствии преобразованная в D. Что же касается L = 50, я понятия не имею, почему его начали использовать.

Теперь мы можем записать римскими цифрами 1964. Это будет выглядеть следующим образом: MDCCCCLXIIII.

Несомненным преимуществом этой системы записи цифр является тот факт, что порядок расположения символов не имеет никакого значения. Если, к примеру, мне придет в голову написать это же число следующим образом: CDCLIIMXCICI, оно все равно будет обозначать 1964. Хотя, я думаю, этого никто не стал бы делать. Если буквы расположены в порядке уменьшения значения цифры (как я сделал это в первый раз), их значительно легче воспринимать и складывать. Поэтому обычно применяется именно такой порядок (за исключением особых случаев).

Когда порядок записи буквенных символов в римских числительных установлен, можно позволить себе некоторые отклонения, если они приведут к каким то упрощениям. Например, мы можем решить, что, если символ с меньшим значением следует за символом, имеющим большее значение, они складываются, если же символ, имеющий меньшее значение, предшествует символу, имеющему большее значение, первое число следует вычесть из второго. Таким образом, VI = 5 + 1, а IV = 5–1. (Вы можете сказать, что тогда IIV — это 3, но дело в том, что удобнее вычитать только одну цифру.) Точно так же LX = 60, a XL = 40, CX = 110, а XC = 90, MC = 1100, а CM = 900.

Значение изложенного выше «принципа вычитания» заключается в следующем: два символа могут выполнить работу пяти. Зачем писать VIIII, если можно ограничиться IX, или DCCCC, если хватит CM? Теперь можно записать 1964 в виде MCMLXIV (семь символов) вместо приведенного ранее числа MDCCCCLXIIII (двенадцать символов). Но теперь порядок записи буквенных символов приобрел значение. Их больше нельзя переставлять. К примеру, MMCLXVI (те же самые семь символов, но в другом порядке) — это уже 2166.

В древности «принципом вычитания» пользовались эпизодически; окончательно он был принят только в Средние века. Могу предложить забавное объяснение причин столь длительной задержки. Это связано с написанием цифры IV (четыре). Эти же символы являются первыми в имени главного римского божества IVPITER. Вполне вероятно, римляне не желали оскорблять своего бога частым употреблением начальных букв его имени. Даже сегодня на циферблатах часов, где использованы римские цифры, вместо IV обычно указывается IIII. И это вовсе не потому, что изготовители часов не приемлют «принципа вычитания»; ведь цифра 9 всегда обозначается IX, а не VIIII.

Используя приведенные выше символы, мы можем довести счет до 4999. Это число будет выглядеть следующим образом: MMMMDCCCCLXXXXVIIII, или, используя принцип вычитания, MMMMCMXCIX. Вы можете предположить, что 5000 = MMMMM, но это не совсем так. Строго говоря, в римской системе символы никогда не повторялись более четырех раз. Для этого всякий раз вводился новый символ: ІІІІІ = V, XXXXX = L, CCCCC = D. Но чему тогда равно MMMMM?

Для 5000 не ввели специальной буквы. В древности в повседневной жизни в таких больших числах просто не было необходимости. Если же ученые или сборщики налогов и умели обращаться с подобными величинами, они не передавали свои навыки простым людям.

Один из способов преодолеть барьер 5000 — использовать черту над буквой для обозначения тысяч. Таким образом, V — это уже не 5, а 5000. Другой способ написания больших чисел — вернуться к примитивному символу I и, добавляя вокруг него круглые скобки, увеличивать число нулей. ((I)) = 10 000, а (((I))) = 100 000. Так же как 500 = I) или D, 5000 = I)), 50 000 = I))).

Как и римляне, греки для обозначения тысяч использовали специальные отметки. Греки даже пошли дальше, введя особые отметки для десятков тысяч и миллионов (по крайней мере, это сделали некоторые греческие писатели). Тот факт, что римляне не довели дело до логического завершения, не является удивительным. Римляне гордились тем, что не являются высокими интеллектуалами. Однако тот факт, что греки здесь тоже оказались не на высоте, удивляет меня безмерно.

Предположим, что вместо введения специальных значков только для больших чисел было решено использовать специальные знаки для всех групп, начиная с единиц. Если придерживаться системы, изложенной мною в начале настоящей главы, где ? обозначает единицы, ? это десятки, + сотни, а = тысячи, тогда можно обойтись одним набором из девяти символов. Мы сможем изображать каждую цифру под соответствующим значком, обозначающим тип группы: = + ? ?. Тогда число 2581 будет изображаться следующим образом (с использованием только букв от A до I и упомянутых выше значков):

= + ? ?

B E H A.

А 5555 будет записано так:

= + ? ?

E E E E.

Причем одинаковые символы E перепутать невозможно, так как один из них обозначает 5, другой — 50, третий — 500, а четвертый — 5000. Используя дополнительные обозначения для 10 000, 100 000, миллионов и т. д., можно записать любую цифру, как бы велика она ни была.

Правда, не думаю, чтобы такая система могла завоевать популярность. Даже если бы какой-нибудь грек придумал нечто подобное, ему наверняка бы не понравилась необходимость аккуратно выписывать эти маленькие значки. Во времена ручного переписывания документов лишние знаки означали дополнительный труд, и писцы наверняка воспротивились бы такой безрадостной перспективе.

Кто-то может решить, что дополнительные обозначения вообще не нужны. В конце концов, соответствующие группы можно записывать справа налево в порядке возрастания величины. Единицы расположатся в крайнем правом ряду, левее будут находиться десятки, дальше сотни и т. д. В таком случае BEHA = 2581, а EEEE = 5555 и без дополнительных значков сверху.

Совершенно верно. Тут возможна другая сложность. А если в каком-то числе не будет группы десятков или единиц? Как быть, к примеру, с числом 10 или 101? Первое состоит из одной группы десятков без единиц, а второе — из групп сотен и единиц, но без десятков. Если использовать принятые обозначения, числа можно записать следующим образом:

и
, только теперь без маленьких значков над буквами обойтись нельзя. Если попробовать, сразу станет ясно, что невозможно отличить A, обозначающую 1, от A, обозначающей 10, или AA = 101 от AA = 11 или AA = 110.

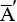
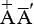
Можно попробовать оставить пробел, обозначив 101 как A A. Но в эпоху ручного переписывания пробел наверняка очень быстро потерялся бы, превратив число в AA. Не менее вероятен и обратный процесс — трансформации AA в A A. И как обозначить пробел в конце числа? Я уверен, если греки и думали о чем-то подобном, то пришли к выводу, что пробелы между символами в числах сделают упрощение практически неприменимым. Они решили бы, что проще обозначить J = 10, a SA = 101; что же касается маленьких значков, ну их к Гадесу!

Никто из греков, даже сам великий Архимед, не подумал, что не обязательно вводить в символ пробелы. Их легко можно заполнить каким-нибудь ничего не значащим символом. Например, поставим вместо пробела значок $. Тогда число 101 можно записать в виде

. Если мы так и поступим, пробелов не будет, да и в значках над буквой больше нет необходимости. Теперь 1 — это A, 10 — A$, 100 — A$$ и т. д. Любое число, как бы велико оно ни было, может быть записано с помощью девяти букв и одного символа, ничего не обозначающего.

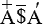
Казалось бы, что может быть проще? После того, как это придумано!

И тем не менее человечеству потребовалось больше пяти тысячелетий, считая от появления первых обозначений чисел, чтобы додуматься до введения в практику символа пустоты. К сожалению, имя гения, которому принадлежит эта величайшая заслуга, осталось неизвестным человечеству. Мы только знаем, что он был индусом и жил не позднее IX века.

Индусы назвали новый символ sunya, что означает «пустой». Этот символ вскоре был принят арабами, назвавшими его sifr. Это слово тоже обозначает «пустой», но уже на арабском языке. Позже оно было преобразовано в современные термины cipher (ноль), а потом через zefirum в zero.

Новая система, названная арабской (поскольку европейцы узнали ее от арабов), очень медленно добралась до стран Запада и вытеснила римскую.

Арабские числительные возникли в тех краях, где никогда не использовали латинский алфавит, поэтому форма цифр ничем не напоминала буквы римского алфавита. С их появлением была устранена путаница между словами и цифрами, а получившая широкое распространение gematria постепенно утратила свое значение и перестала занимать умы широких масс.

Арабские цифры, которыми все мы сегодня пользуемся, — это 1, 2, 3, 4, 5, 6, 7, 8, 9 и конечно же 0. Мы привыкли к этим цифрам и, пожалуй, даже не осознаем, насколько полно. К примеру, если в настоящей главе вам что-то показалось странным или сомнительным, то, возможно, оттого, что я в ней намеренно не приводил ни одного арабского числительного.

Мы все знаем, насколько появление арабских цифр упростило арифметические вычисления. Они избавили людей от множества ненужных забот, в основном благодаря присутствию зеро, которое является воистину бесценным. Необыкновенная важность зеро нашла свое отражение и в английском языке. Ведение арифметических подсчетов носит слегка устаревшее название ciphering (cipher — ноль), а процесс расшифровки какого-либо кода — deciphering.

Теперь, если вы вернетесь к названию этой главы, то поймете, что его следует понимать буквально. Ничего считается! И появление специального символа для обозначения ничего является величайшим открытием человечества.

<<< Назад Глава 11 Забудьте об этом!

Вперед >>> Глава 13 Буквой с обозначается скорость света в пустоте