Книга: Вселенная

Глава 10 Обновление базы знаний

Глава 10

Обновление базы знаний

Признав, что каждый из нас ориентируется на богатый набор априорных субъективных вероятностей, важно уточнять эти вероятности по мере поступления новой информации. Для этого нужно дать более строгую формулировку теоремы Байеса.

Вернёмся к нашей дружеской партии в покер. Мы знаем, какие карты у нас на руках, но не знаем карт оппонента. Таким образом, мы оказываемся в ситуации, когда возможны самые разные «посылки» (гипотезы об истинности чего-либо), и при этом имеем исчерпывающий список всех возможных посылок. В данном случае посылки соответствуют всем различным картам, которые могут прийти нашему сопернику в исходной покерной раздаче (ничего, пара, что-то лучше пары). Иными словами, они годятся в качестве возможных интерпретаций любых утверждений нашего друга (утверждение истинно; он искренне считает его истинным, но оно ошибочно; утверждение ложно). Также имеем здесь набор конкурирующих онтологий (натурализм, вера в сверхъестественное, нечто более экзотическое).

Каждой рассматриваемой посылке мы присваиваем априорную субъективную вероятность. Для наглядности представим субъективные вероятности, разложив песчинки по баночкам. Каждая баночка соответствует определённой посылке, а число песчинок в баночке пропорционально субъективной вероятности, присваиваемой данной посылке. Субъективная вероятность суждения X — это просто доля общего числа песчинок, соответствующая числу песчинок, оказавшихся в баночке X:

Назовём это «правилом песчинок».

Теорема Байеса указывает, как уточнять такие вероятности по мере поступления новой информации. Допустим, мы получили информацию в виде каких-то данных — например, узнали, сколько карт набрал соперник. Тогда из каждой баночки мы удаляем некоторое количество песка, соответствующее вероятности того, что мы не получили бы этой информации, окажись соответствующая посылка верной. Если мы считаем, что соперник заменит ровно одну карту всего в 10% случаев, если у него есть пара, то, как только он заменит одну карту, мы удаляем 90% песчинок из банки, на которой написано «пара». Затем проделываем аналогичную вещь со всеми остальными банками. В результате наше правило песчинок вновь подтверждается: субъективная вероятность посылки X равна числу песчинок в баночке X, делённому на общее число песчинок во всех баночках.

В ходе этой процедуры априорные субъективные вероятности перевзвешиваются и дают в итоге апостериорные субъективные вероятности. Можно начать с ситуации, когда в нескольких баночках содержится примерно поровну песчинок — это означает, что субъективные вероятности равны. Но затем мы получаем новую информацию, которая будет вероятна при одних посылках и маловероятна при других. Мы убираем совсем немного песка из тех баночек, для которых эта информация была вероятна, и много песка из тех, для которых маловероятна. Получается, что в баночках, которым соответствует наибольшая степень вероятности, скапливается больше песка — их апостериорная субъективная вероятность оказывается выше. Разумеется, если наша априорная субъективная вероятность для одной из посылок была гораздо выше, чем для альтернативных версий, то нам придётся удалить из «её» баночки очень большое количество песка (собрать много данных, кажущихся маловероятными при данной посылке), чтобы присущая данной посылке субъективная вероятность стала небольшой. Когда априорные показатели очень низки или очень высоки, нам понадобятся нетривиальные данные, чтобы эти субъективные вероятности изменились.

* * *

Рассмотрим другой пример: вы, старшеклассник, влюбились в девушку и хотите пригласить её на выпускной бал. Вопрос: она согласится или откажет? Итак, есть две разные посылки: «да» (она пойдёт с вами на выпускной бал) или «нет» (откажет), причём для каждой посылки есть субъективная априорная вероятность. Будем оптимистичны и присвоим субъективную вероятность 0,6 положительному ответу и 0,4 отрицательному (разумеется, общая субъективная вероятность всегда должна давать в сумме единицу). Ставим две баночки, в одну насыпаем 60 песчинок («да»), в другую — 40 («нет»). Общее число песчинок не имеет значения — важны лишь относительные пропорции.

Далее мы собираем информацию и на её основании уточняем априорные вероятности. Вы стоите у шкафчика с одеждой, а мимо по коридору идёт ваша пассия. Она с вами поздоровается или просто пройдёт мимо? Это зависит от её отношения к вам: гораздо вероятнее, что она остановится и поприветствует вас, если также склонна составить вам компанию на выпускной. Вы недурно разбираетесь в человеческих взаимоотношениях и понимаете, что, если верна посылка «да», девушка остановится и поприветствует вас в 75% случаев, а в 25% случаев просто пройдёт мимо (может быть, она просто не в духе). Однако, если верна посылка «нет», ситуация уже не столь радужная: в 30% случаев девушка скажет «привет», а в 70% случаев пройдёт мимо. Таковы шансы на получение различной информации при верности тех или иных посылок. Давайте соберём данные и уточним наши априорные субъективные вероятности!

Допустим, к вашей радости, пассия останавливается и говорит: «Привет!». Каковы шансы, что она примет приглашение на выпускной бал? Преподобный Байес предписывает нам убрать 25% песчинок из банки «да» и 75% песчинок из банки «нет» (в обоих случаях это соответствует доле случаев, в которых наблюдаемый результат не состоялся бы). У нас осталось 60 ? 0,75 = 45 песчинок в баночке «да» и 40 ? 0,30 = 12 песчинок в баночке «нет». Согласно вышеприведённому правилу песчинок, уточнённая субъективная вероятность для «да» — это число песчинок в баночке «да» (45), делённое на общее число песчинок в обеих баночках (45 + 12 = 57). Получается 0,79.

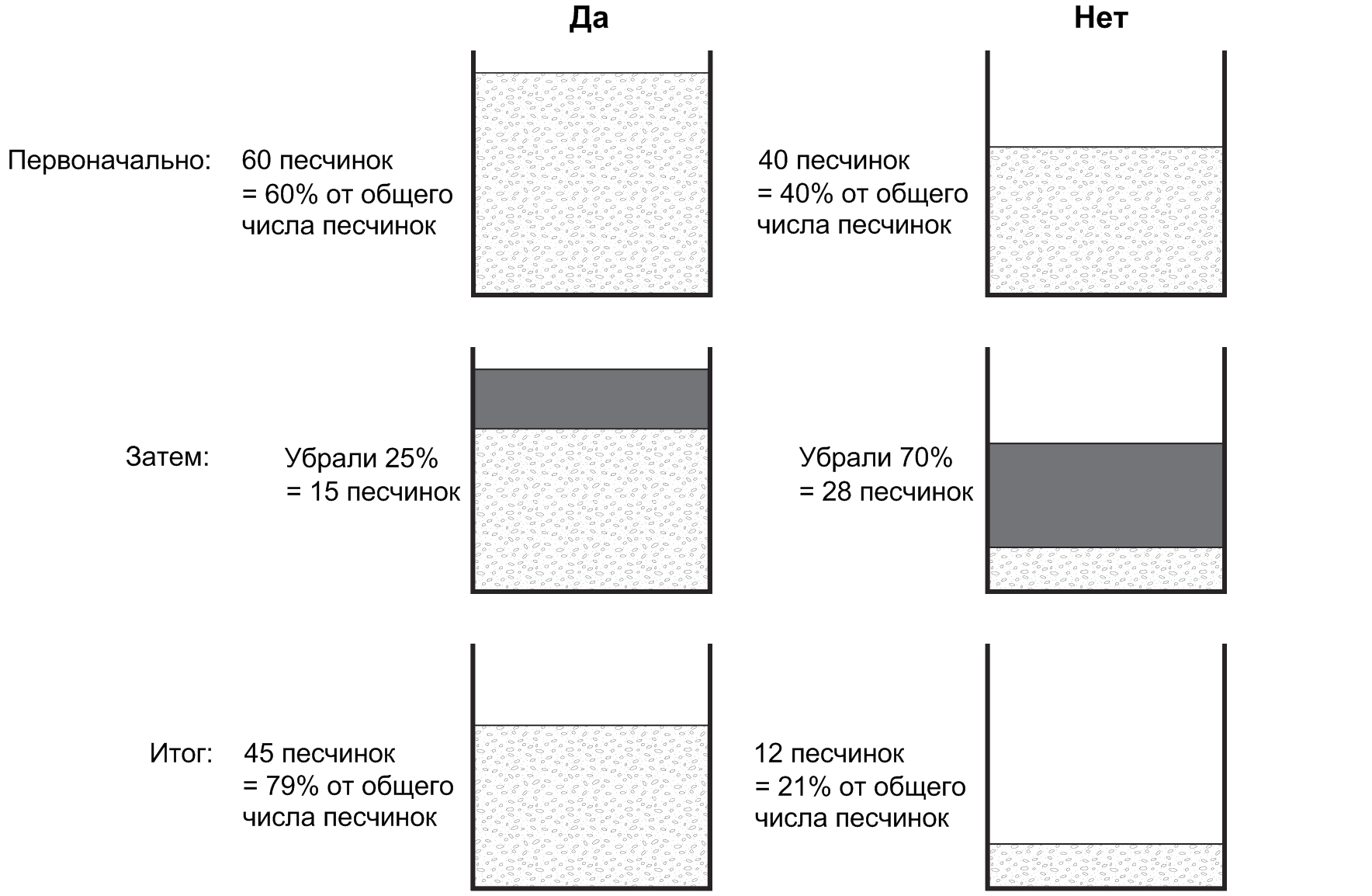
Неплохо! Субъективная вероятность положительного ответа на приглашение повысилась с 60% (априорная) до 79% (апостериорная), притом что девушка просто остановилась и поздоровалась с вами! Думаю, уже надо костюмчиком озаботиться.

Однако постарайтесь уловить под грузом математических деталей основной посыл. В байесовской философии любая посылка (суждение) о мире, которая может быть истинной или ложной, получает априорную субъективную вероятность. Каждая такая посылка также сопровождается набором объективных вероятностей: шансов на истинность различных иных фактов при условии истинности данной посылки. Всякий раз, получая новую информацию, мы корректируем степень уверенности, умножая исходную субъективную вероятность на соответствующую объективную вероятность сделать такое наблюдение при условии истинности каждой из посылок. В виде формулы это выглядит следующим образом:

Это суть теоремы Байеса. Символ «?» означает «пропорционально». Он просто напоминает: нужно удостовериться в том, что все значения субъективной вероятности в сумме должны давать единицу.

* * *

В некоторых случаях кажется естественным задавать числовые значения субъективной вероятности: например, если речь идёт о покерных раздачах или подбрасывании монетки, где можно запросто подсчитать все возможности. Кроме того, о «вероятности» часто говорят, рассуждая о будущих событиях: «Вероятность того, что залётный астероид врежется в Землю и вызовет массовое вымирание, составляет менее одного процента».

Однако байесовский подход более универсален. Он напоминает о том, что мы присваиваем значения субъективной вероятности и корректируем их, обдумывая любое фактическое предположение о мире, которое может оказаться истинным или ложным. Есть ли Бог? Можно ли объяснить опыт наших внутренних переживаний в чисто физических терминах? Существуют ли объективные стандарты «правильного» или «неправильного»? Все возможные ответы на такие вопросы — это посылки, причём любому из них каждый человек присваивает ту или иную субъективную вероятность (хотя может этого и не признавать), которую корректирует по мере поступления новой информации (хотя может делать это и неправильно).

Теорема Байеса позволяет количественно оценить нашу степень уверенности в чём-либо, но также помогает не забыть, каким вообще механизмам подчиняется вера. Размышляя об априорных субъективных вероятностях таким образом, можно извлечь ряд полезных уроков.

О важности предшествующих убеждений. Пытаясь понять, какие представления о мире истинны, каждый начинает эту игру, имея определённые собственные представления о том, какие предположения вполне убедительны, а какие — относительно маловероятны. Это не досадная ошибка, которую нам следовало бы исправить; это абсолютно необходимый элемент рассуждений, когда мы располагаем неполной информацией. Когда же речь заходит о понимании фундаментального устройства реальности, полной информацией не обладает никто.

Априорные субъективные вероятности — отправная точка для дальнейшего анализа, и сложно сказать, какие из них «верны», а какие «ошибочны». Однако в данном случае следует упомянуть несколько удобных железных правил. Пожалуй, наиболее очевидное таково: сравнительно простые теории должны получать более высокую априорную субъективную вероятность, чем более сложные. Это не означает, что более простые теории всегда верны; однако, если простая теория ложна, мы узнаем об этом, собрав информацию. Как выразился Альберт Эйнштейн, «пусть это будет просто, просто как только можно, но не проще».

Иногда о простоте легко судить, порой — не очень. Сравним три конкурирующие теории. Согласно первой, движение планет и спутников в Солнечной системе подчиняется, как минимум с очень хорошим приближением, ньютоновской теории тяготения и движения. Вторая теория утверждает, что ньютоновская физика вообще не работает, но к каждому небесному телу приставлен ангел и эти ангелы ведут планеты и спутники по орбитам, причём эти траектории совершенно случайно совпадают с теми, что вычислил бы Ньютон.

Большинству из нас, вероятно, покажется, что первая теория проще второй — она даёт те же результаты, но без привлечения столь неопределённых сущностей, как ангелы. Однако есть и третья теория: ньютоновское тяготение определяет движение всех тел в Солнечной системе, кроме Луны, которую направляет ангел, и этот ангел просто старательно следует траектории, которую предсказывает теория Ньютона. Вполне бесспорно, что, независимо от вашего мнения о первых двух теориях, третья определённо сложнее первых двух. В ней задействованы все механизмы первой и второй теории, а её эмпирические прогнозы на практике ничуть не лучше. Следовательно, мы вправе присвоить ей очень низкую априорную субъективную вероятность. (Этот пример кажется несерьёзным, но аналогичные ходы постоянно применяются в рассуждениях о развитии биологической эволюции или о природе сознания.)

Некоторым не нравится байесовский акцент на априорном, поскольку априорное скорее субъективно, чем объективно. Да, так и есть. Ничего не поделаешь — нужно же с чего-то начинать. С другой стороны, в идеале можно объективно определить вероятность того или иного наблюдения. Если у вас есть определённая теория об устройстве мира, причём эта теория точна и хорошо проработана, вы можете с уверенностью сказать, каковы шансы наблюдения тех или иных данных при условии, что ваша теория верна. На практике мы часто затрудняемся оценить теории, которые проработаны не столь строго. (Посылка «Сознание выходит за рамки физической природы» разумна, однако она слишком расплывчатая, чтобы делать на её основании количественные прогнозы.) Тем не менее наша задача — попытаться определить посылки максимально точно, настолько, чтобы их можно было использовать для объективной оценки вероятности различных наблюдений.

Любой имеет право на априорные предположения, но объективная вероятность личной не бывает.

Факты должны помогать прийти к консенсусу. Просматривается проблема: а вдруг многим людям вообще будет сложно прийти к согласию из-за априорных убеждений? Если идея «Бог создал Вселенную» для меня обладает субъективной вероятностью 0,000001, а для вас — 0,999999, то, чтобы изменить точку зрения, любому из нас потребуется серьёзно её откорректировать на основе наблюдений.

На практике это реальная проблема. У людей есть такие убеждения, которые просто никогда не меняются, — на байесовском языке можно сказать, что им соответствует априорная вероятность 0 или 1. Это очень плохо, и в реальном мире мы должны научиться как-то справляться с этой проблемой.

Тем не менее, в принципе, все мы стараемся быть честными и недогматичными, готовы менять мнение с учётом новой информации — в конце концов всегда побеждают факты. Можно присвоить какой-либо идее очень высокую априорную субъективную вероятность, но, если эта идея предполагает, что определённый результат будет возникать всего в одном проценте случаев, а он всё возникает и возникает, честная корректировка по Байесу в итоге вынудит вас присвоить этой идее очень низкую апостериорную вероятность. Например, вы можете задать очень высокую априорную субъективную вероятность для тезиса «если буду пить кофе, то смогу предсказывать будущее». Затем вы пьёте кофе, делаете те или иные предсказания, убеждаетесь, что они не выполняются, и вносите необходимую корректировку. Если делать это достаточно долго, то ваше априорное суждение рухнет под напором фактов. Это называется «изменить мнение», это хорошо. Более того, поскольку объективная вероятность считается объективной, чем больше данных мы собираем, тем ближе каждый из нас подходит к одному и тому же набору окончательных убеждений о мире.

Предполагается, что этот механизм должен работать именно так. От каждого зависит, насколько добросовестно его придерживаться.

Факты в пользу одного из вариантов автоматически заставляют усомниться в других. Допустим, мы сравниваем две посылки, X и Y, и наблюдаем результат, который с вероятностью 90% происходит в случае X и с вероятностью 99% в случае Y. Согласно теореме Байеса, при получении такой информации априорная субъективная вероятность посылки X будет уменьшаться.

Это может показаться нелогичным. В конце концов, если посылка X верна, то у нас 90-процентные шансы получить искомый результат — как такое наблюдение может свидетельствовать против этой посылки? Ответ таков: при другой теории данный результат даже ещё более вероятен. Возможно, изменение априорных субъективных вероятностей будет и невелико, но оно всегда будет. Итак, если вы нашли объяснение какому-либо событию в рамках определённой теории, отсюда ещё не следует, что это событие не понижает субъективной вероятности данной теории. Верно и обратное: если то или иное наблюдение подкрепляет определённую теорию, но мы получили противоположное наблюдение, то результат неизбежно понизит субъективную вероятность данной теории.

Рассмотрим две теории: Бог есть (теизм) и Бога нет (атеизм). При этом допустим, что мы живём в таком мире, где религиозные тексты различных культур в глобальном масштабе и на протяжении истории полностью согласуются друг с другом. По существу, в них излагаются одни и те же сюжеты и проповедуются общие идеи, хотя авторы этих текстов никоим образом не могли контактировать друг с другом.

Разумеется, любой сочтёт, что это доказательство в пользу теизма. Конечно, такую общую непротиворечивость можно каким-то затейливым образом объяснить и в рамках атеизма: может быть, у людей есть общий стимул рассказывать одни и те же истории и это свойство мы приобрели в ходе эволюции. Однако мы не можем отрицать, что теизм даёт более простое объяснение: Бог ниспослал своё откровение множеству разных народов.

Если это истинно, то на уровне чистой логики верно и то, что противоречивость священных текстов — это факт, свидетельствующий против теизма. Если данные D повышают для нас субъективную вероятность теории X, то данные «не D» обязательно её снижают. Возможно, такую противоречивость будет несложно объяснить, и не о отказываясь от истинности теизма: может быть, у Бога есть любимчики или же не все слушали внимательно. Это эпизод оценки вероятностей, но качественного результата он не меняет. Если мы будем честны, то уровень субъективной вероятности теории всегда должен снижаться, если мы получаем наблюдения, которые лучше согласуются с другими теориями. Возможно, изменение будет невелико, но оно будет.

Все факты важны. Легко притворяться грамотным байезианцем, а на деле жульничать, учитывая не все факты, а лишь некоторые.

Друг вам признаётся, что верит в лох-несское чудовище. Он говорит: «Есть снимки — это серьёзные доказательства». Разумеется, вы должны признать, что вероятность получения таких снимков гораздо выше, если Несси существует, чем если её нет.

Да, но это ещё не всё. Во-первых, априорная вероятность существования монстра в далёком шотландском озере должна быть очень мала. Однако если вы получите достаточно убедительные доказательства, то это мнение придётся пересмотреть. Но несколько некачественных фотоснимков — ещё не все факты. Мы также должны учитывать и все попытки отыскать чудовище в озере Лох-Несс, которые оказались тщетными. Что уж говорить о том, что первая знаменитая фотография Несси в итоге была признана мистификацией. Мы не можем выбирать удобные факты и учитывать только их — все релевантные данные нужно принимать во внимание.

Теорема Байеса — одно из озарений, позволяющих нам полностью изменить образ жизни. Каждый из нас имеет массу разнообразных убеждений, соответствующих всевозможным посылкам или противоречащих им. Байес учит нас: 1) никогда не присваивать любому такому убеждению абсолютную истинность; 2) всегда быть готовым откорректировать субъективную вероятность, если выяснятся новые факты и 3) понимать, как именно такие факты изменяют имеющиеся значения субъективной вероятности. Это карта, позволяющая нам всё ближе и ближе подбираться к истине.