Книга: Серебристые облака и их наблюдение

§ 15. Определение высот серебристых облаков

§ 15. Определение высот серебристых облаков

Определить высоты серебристых облаков можно из одновременных (корреспондирующих) фотографий, полученных с двух концов базиса, длина и ориентировка которого известны. Существует несколько способов определения высот серебристых облаков. Мы здесь изложим сравнительно простой способ, предложенный М. А. Дирикисом и Ю. Л. Францманом.

Введем прямоугольную геоцентрическую систему координат с началом в центре Земли. Ось X направим к точке пересечения экватора с начальным (гринвичским) меридианом, ось Y — к точке экватора с восточной долготой 90°, ось Z — к северному полюсу Земли.

Далее введем две топоцентрическне системы координат с началом в каждом из двух пунктов наблюдений. Оси расположим параллельно осям основной геоцентрической системы.

Определенные путем измерения на фотографиях горизонтальные координаты точки облака h, А переводим в экваториальные координаты t, ? по известным формулам

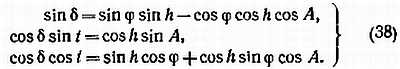
В формулах (38) ? — широта пункта наблюдения, ? — склонение, t — часовой угол данной точки облака. Далее для сокращения записи там, где формулы одинаковы для обоих пунктов, мы будем писать индекс i (i = 1, 2). Топоцентрические координаты точки С облака будут равны

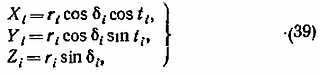
где r_i — расстояния до точки С от обоих наблюдательных пунктов по прямой (по лучу зрения). Введем обозначения (для краткости)

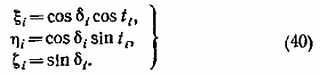
Тогда получим следующую систему из шести уравнений пятью неизвестными — геоцентрическими координатами точки С (Х_с, Y_c, Z_c) и расстояниями r₁, r₂:

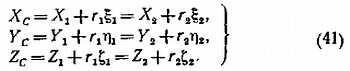
Эту систему можно решить методом наименьших квадратов, изложенным в Постоянной части «Астрономического календаря» (7-е изд. — М.: Наука, 1981, с. 521–532). Для тех, кто не знаком с этим методом, можно рекомендовать следующий порядок вычислений.

Отвлечемся на время от левых равенств в системе (41) и от величин Х_с, Y_c, Z_c. Тогда у нас останутся три условных уравнения с двумя неизвестными r₁, r₂. Их решение по методу наименьших квадратов дает

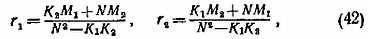
где введены обозначения

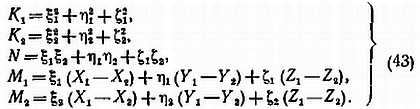
Подставляя r₁, r₂ в уравнения (41), получим значения Х_с, Y_c,Z_c. Из двух значений каждой из этих величин (по i = 1 и i = 2) берем среднее. Затем находим радиус-вектор точки С относительно центра Земли р_с,

p_c = ?(Х²_с + Y²_c + Z²_c), (44)

и наконец, высоту точки С серебристого облака

H = p_c — R, (45)

где R — радиус Земли на широте проекции серебристого облака, которую можно найти по формуле

?' = arcsin (Z_c/p_c); (46)

аналогично долгота проекции точки С равна

? = arctg (Y_x/X_c). (47)

Значения R для данной широты ? приведены в Приложении 4. Там же даны поправки для перевода геоцентрической широты ?' (получаемой из формулы (46)) в географическую широту ?. В среднем для зоны появлений серебристых облаков ? — ?' = 10'.

Таким образом, определение высот серебристых облаков методом Дирикиса-Францмана — операция несложная, но требует выполнения многих измерений и вычислений. Лучше всего эти расчеты производить на ЭВМ. Те кружки или группы наблюдателей серебристых облаков, которые имеют такую возможность (используя ЭВМ астрономических или иных научных учреждений, шефствующих предприятий и т. д.), должны составить программу и заложить в нее результаты измерений по всем фотографиям, полученным с двух пунктов. Формулы элементарны, и поэтому любая ЭВМ выдаст результаты за очень короткий срок.

Тем, кто не имеет такой возможности, придется считать на микрокалькуляторах или с помощью таблиц, что тоже не представляет принципиальных трудностей. Придется, правда, потрудиться, но зато наблюдатели и вычислители будут вознаграждены интересными и ценными результатами, которые они получат.