Книга: Серебристые облака и их наблюдение

$ 14. Развертка полей серебристых облаков на земную поверхность и определение их движений

$ 14. Развертка полей серебристых облаков на земную поверхность и определение их движений

Получить хорошие фотографии или кинокадры серебристых облаков — это только полдела. Дальше нужно их обработать, чтобы получить те или иные научные результаты, в зависимости от поставленной задачи. Об этом уже говорилось в § 10.

Здесь мы опишем простую методику перехода от фотографии, представляющей собой изображение серебристых облаков в проекции на небесную сферу, к схеме пространственного расположения этих образований в проекции на земную поверхность. Такая операция называется развертыванием, а ее результат — разверткой.

Для успешного решения этой задачи необходимо знать следующие величины:

1) Фокусное расстояние фотокамеры; как правило, оно слегка отличается от указанного на оправе объектива; однако в первом приближении можно использовать номинальное значение F.

2) Положение центра снимка и его горизонтальные координаты.

3) Положение линии горизонта на снимке.

4) Географические координаты наблюдательного пункта.

Рассмотрим простой способ определения координат центра снимка. Для его обозначения на снимке проводим простым карандашом по эмульсии негатива близ его центра отрезки диагоналей, пересечение которых и обозначит центр снимка. Для удобства делаем в этом месте легкий накол иголкой.

Для определения координат этого центра, азимута A₀ и высоты h₀, необходимо иметь на снимке несколько точек с известными координатами A, h. Это могут быть городские сооружения (вершина шпиля башни, заводской трубы и т. д.) или специально установленные столбы с лампочками наверху, о которых уже говорилось. Не рекомендуется выбирать в качестве ориентиров верхушки деревьев или тонкие приемные телеантенны, так как они могут раскачиваться ветром. Координаты выбранных ориентиров определяются с помощью теодолита.

В качестве опорных точек можно использовать и звезды, для которых по известному моменту съемки и экваториальным координатам вычисляются горизонтальные координаты А, h. Как это делать, рассказано в Постоянной части «Астрономического календаря» и в учебниках общей астрономии для вузов. В значения высоты звезд вводятся поправки за рефракцию.

Если аппарат имеет наклон оптической оси к плоскости горизонта на угол ? (? ~= 10°), то целесообразно ввести вспомогательную систему сферических координат, наклоненную на угол ? к горизонтальной системе (рис. 40).

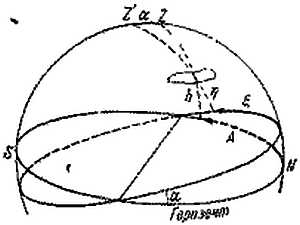
Рис. 40. Вспомогательная система сферических координат ?, ?.

Роль «азимута» будет играть угол ? роль «высоты» — угол ?. На снимке мы с помощью прямоугольной прозрачной палетки или измерительного прибора измеряем прямоугольные координаты деталей х, y отсчитываемые от найденного нами центра снимка. Если координаты приходится отсчитывать от другого начала (обозначим их х', у'), то нужные нам координаты х, у мы найдем по формулам

x = х' + х_c, у = у' — у_c, (23)

где x_c, у_с — координаты центра снимка в той же системе.

Далее по значениям х, y находим сферические координаты ?, ? по формулам

tg ? = x/F, (24)

tg ? = (y/F)?(cos ?), (25)

При этом мы полагаем, что координаты центра снимка ?₀— 0, ?₀ = 0, и учитываем знаки каждой координаты, считая их положительными вверх и вправо от центра. Найдя для каждого ориентира значения ?, ?, вычисляем разности А — А₀ по формуле

sin (А — А₀) = (cos ??sin ?)/cos h, (26)

Значения A, h нам известны из прямых измерений теодолитом (а для звезд из вычислений). Точки, для которых А — А₀ > 10° и h — h₀ > 10°, отбрасываем, для остальных по А — А₀ и известным А находим A₀ и из полученных значений (которые должны слабо отличаться друг от друга) находим среднее. Это и будет азимут центра снимка. Его высота h₀ находится по формуле

h₀ = (h — ?)/cos (A — A₀), (27)

Значения h₀, полученные по разным ориентирам, тоже усредняем. Отдельные значения h₀ должны отличаться друг от друга не более чем на 2–3'. Если получатся более сильные расхождения, значит, допущены ошибки в измерениях или вычислениях, и их надо проверить.

До сих пор мы предполагали, что изображение линии горизонта на снимке параллельно нижней стороне кадра. Однако если мы применяем три аппарата для панорамной съемки, как показано на рис. 37, для двух крайних аппаратов это условие выполнено не будет. Поэтому приведем формулы, с помощью которых можно построить изображение линии горизонта в этом случае.

Уравнение этой линии в прямоугольных координатах имеет вид[7])

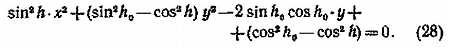
Поскольку Нам известно h₀ и для каждого ориентира его высота h, мы можем решить квадратное уравнение (28) относительно у (х берем из измерении) для каждого ориентира.

Откладывая затем отрезки, равные у, вниз от точки ориентира, получим ряд точек горизонта, которые должны лечь на дугу малой кривизны, близкую к прямой линии.

Однако полученная линия горизонта — лишь первое приближение, поскольку координаты х, использованные нами в уравнении (28), измерены в системе, слегка повернутой относительно проекции линии горизонта. Выйти из положения можно двумя способами. Во-первых, можно заново измерить значения х, у, сориентировав ось х палетки или измерительного прибора параллельно найденной в первом приближении линии горизонта, и затем повторить расчет по формуле (28). Мы получим новую линию горизонта, которая должна пройти близко от первой или даже может совпасть с ней.

Второй способ состоит в том, что измеряется угол поворота ? найденной в первом приближении линии горизонта относительно оси, проходящей параллельно нижней стороне кадра. Новые координаты х, у выразятся тогда через старые х', у' формулами

x = x'?cos ? + y'?sin ?,

y = — x'?sin ? + y'?cos ?, (29)

причем угол ? считается положительным, если поворот осей координат происходит против часовой стрелки, и отрицательным, если по часовой стрелке. После этого по значениям х, у вновь находим линию горизонта.

Оба способа целесообразно применять параллельно, для взаимного контроля. Подчеркиваем, что все эти расчеты, измерения и построения нужно делать не для каждого кадра, а лишь один раз для данной ориентации аппарата. Поэтому целесообразно заранее позаботиться о фиксации положения как аппаратов на установочной доске, так и самой доски на столбе (столе). Этим мы намного облегчим себе работу по обработке фотографий.

Необходимо еще раз подчеркнуть необходимости производить математическую обработку фотографий серебристых облаков, без которой они превратятся в красивые, но почти бесполезные картинки. Не надо бояться вычислений. Напротив, надо научиться быстро и правильно вычислять и, что не менее важно, правильно и аккуратно записывать результаты вычислений. Ни в коем случае нельзя вычислять на клочках бумаги, а тем более — выбрасывать потом эти листки. Все вычисления надо вести в специальной тетради, причем записываются не только окончательные, но и все промежуточные результаты вычислений. Формулы, по которым ведутся вычисления, выписываются сверху, после чего все обозначения, к числа располагаются столбиками. Арифметические знаки действий (плюс, минус и др.), а также знак равенства не пишутся. Перед отрицательными величинами ставится знак минус. Приведем пример расположения вычислений (табл. 2).

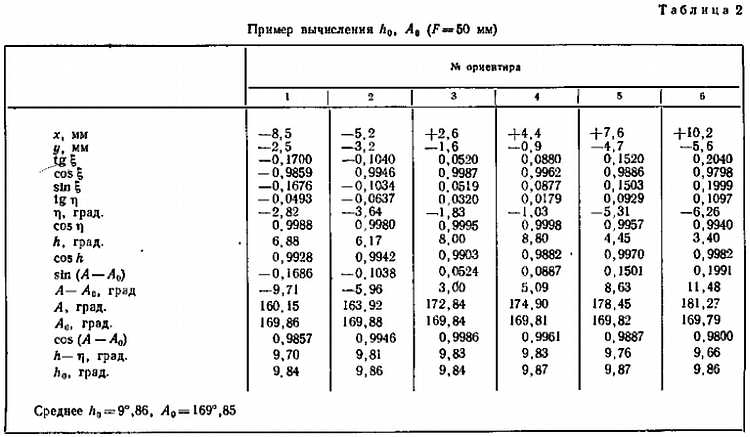
Хотя согласно правилам, изложенным выше, данные по ориентиру № 6 следует исключить из обработки, так как (А — А₀) > 10°, этот ориентир дает значение h₀ в хорошем согласии с остальными и лишь А₀ для него «отскакивает» на 0°,06, т. е. на 3',6 от среднего значения.

Сейчас в продаже имеются микрокалькуляторы «Электроника», доступные по цене и позволяющие быстро вычислять логарифмы, тригонометрические и обратные тригонометрические функции. При использовании микрокалькуляторов надо иметь в виду, что и в работе с ними может быть допущена ошибка (как вычислителем — например, нажал не на ту кнопку, так и самим прибором), поэтому рекомендуется каждый расчет проводить дважды; лучше всего, если это делают разные вычислители (это называется вычислением «в две руки»). При наличии расхождений производится третий расчет. Если расчеты производятся с помощью таблиц и арифмометра (когда нет калькулятора), это тем более необходимо.

Итак, все необходимые величины нам известны, и можно приступить к операции развертывания фотографии.

Для измерения координат серебристых облаков на снимках удобнее всего приготовить специальную палетку. Если фотографирование ведется с малоформатной камерой типа «Зенит», измерять самый кадр неудобно, и нужно воспользоваться фотоувеличителем. Заложив кадр в фотоувеличитель, кладем на столик лист бумаги и подбираем масштаб увеличения, который в дальнейшем будем использовать при обработке всех снимков. Под этот масштаб мы и рассчитаем палетку.

Эффективное фокусное расстояние F', соответствующее масштабу увеличенного изображения, равно

F' = F?(L/l), (30)

где F — фокусное расстояние объектива камеры, L и l — длины одних и тех же отрезков на увеличенном и оригинальном изображениях (это может быть любая из сторон кадра или его диагональ).

Формулы для расчета прямоугольных координат узловых точек палетки имеют вид

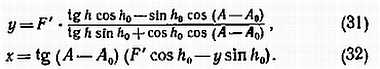
Задавая значения h, А через градус и зная F', h₀, A_0, мы без труда найдем х, у для значений h, А — А₀, соответствующих целым градусам. Нанеся по значениям х, у точки на лист бумаги, соединим их отрезками прямых (из-за малой кривизны дуг нет надобности пользоваться лекалом). Пример такой палетки для F' = 250 мм и h₀ = 6°07? представлен на рис. 41.

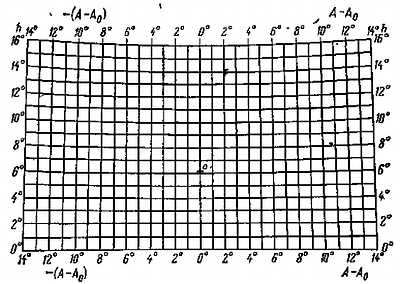
Рис. 41. Палетка для измерения координат серебристых облаков для F' = 250 мм и h₀ = 6°07?

Теперь мы можем начать измерения. Накладываем палетку на изображение поля серебристых облаков так, чтобы линия горизонта и оптический центр, наколотый иголкой, на изображении совпали с соответствующей линией и точкой на палетке (рис. 42).

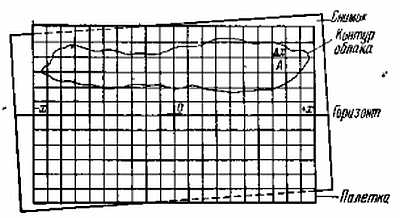
Рис. 42. Наложение палетки на снимок серебристых облаков.

Затем измеряем координаты h, А — A₀ (которые потом переводим в h, А) тех точек поля серебристых облаков, которые мы хотим отобразить на земную поверхность.

Расстояние S от точки наблюдения до проекции точки серебристого облака с учетом рефракции можно вычислить по следующей формуле, выведенной М. И. Буровым:

S = 7429?(-tg h + ?(tg²h + 0,0221)), (33)

где S — расстояние в километрах. Еще проще определить это расстояние с помощью номограммы, изображенной на рис. 43.

Рис. 43. Номограмма для определения расстояний.

Значения S приведены также в Приложении 3 в конце книги.

Определив S, берем хорошую географическую карту, помечаем на ней пункт наблюдений и откладываем от него расстояние S каждой точки поля серебристых облаков в направлении, соответствующем ее азимуту А (при этом надо помнить, что азимут 180° соответствует направлению на север). Мы получим проекции этих точек на земную поверхность. По отдельным точкам можно восстановить очертания всего облачного поля. Для удобства следует изготовить отпечаток снимка, зеркальный относительно линии горизонта: на этом отпечатке верх и низ поменяются местами, а левая и правая стороны останутся соответственно слева и справа. Такой отпечаток будет передавать общую конфигурацию облачного поля, но с перспективными искажениями. Напомним, что верхние части поля расположены ближе к нам, чем нижние, поэтому мы и рекомендуем изготовить такой зеркальный отпечаток. Кроме того, на нем будет наглядно видна волновая структура облаков (см. рис. 12).

Нанеся на карту положения тех или иных деталей по нескольким последовательным снимкам, измеряем затем по карте их смещения между двумя соседними положениями. Поделив эти смещения на интервалы времени между снимками, получим значения скоростей движения этих деталей.

Впрочем, производить измерения по карте не обязательно — необходимые нам смещения можно вычислить. Пункт наблюдения и оба положения проекции детали серебристого облака образуют сферический треугольник на поверхности земного шара (рис. 44), в котором мы без труда находим две стороны s₁, s₂ (угол между^ними ? = А₁ — А₂ нам известен), зная расстояния S₁, S₂:

s_1,2 = (180/?)?(S_1,2/R). (34)

Здесь R = 6389 км — радиус кривизны земной поверхности в широтном поясе, где наблюдаются серебристые облака. Третью сторону треугольника ? найдем по формулам

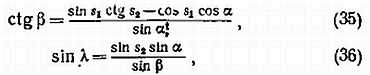
где ? — вспомогательный угол, противолежащий стороне s₂.

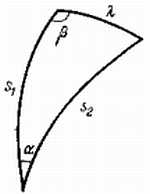
Рис. 44. Сферический треугольник на поверхности Земли (к определению смещения серебристых облаков).

От величины ? — дуги смещения в градусах — делаем переход к смещению L в километрах по формуле

L = (???/180)?R. (37)

Поделив L на интервал времени t, получим скорость движения данной детали серебристого облака. Скорости надо свести в таблицу для данной ночи, и если они мало отличаются друг от друга, найти среднюю скорость. Потом надо сопоставить между собой скорости движения для разных ночей, построить график распределения по скоростям.