Книга: Солнечная система (Астрономия и астрофизика)

Импульсные перелеты

Итак, у нас в запасе внушительный набор орбит, по которым можно двигаться долго-долго, не затрачивая ни малейших усилий. Но как попасть туда? Будем считать, что мы уже вышли в космос на круговую орбиту искусственного спутника Земли. А теперь нам надо перейти на более высокую орбиту. Тоже круговую и лежащую в той же плоскости. Имея супер-ракету, можно перелететь с орбиты на орбиту множеством способов. Но современные ракеты пока не позволяют развивать скорости в сотни километров в секунду, так что не все способы реализуемы. А поскольку каждый лишний грамм груза на борту — все равно что кирпич в рюкзаке у туриста, из возможных способов следует выбрать оптимальный, т.е. требующий минимального количества топлива.

Реактивные двигатели работают без перерыва несколько минут, тогда как перелеты длятся часы, а межпланетные — месяцы и годы. Так что можно считать без большой ошибки, что космический корабль практически мгновенно получает добавку скорости (как говорят, к аппарату прикладывается импульс скорости). Чтобы уйти с орбиты старта, нужен по крайней мере один импульс ?₁. Чтобы остаться на орбите финиша — еще один ?₂. Так называемая характеристическая скорость ?₁+?₂, а с ней и расход топлива, будут минимальными, если импульсы прикладывать по касательным (рис.12). Это было доказано еще в 1920-е гг. В. Гоманом в Германии и Ф.А. Цандером у нас.

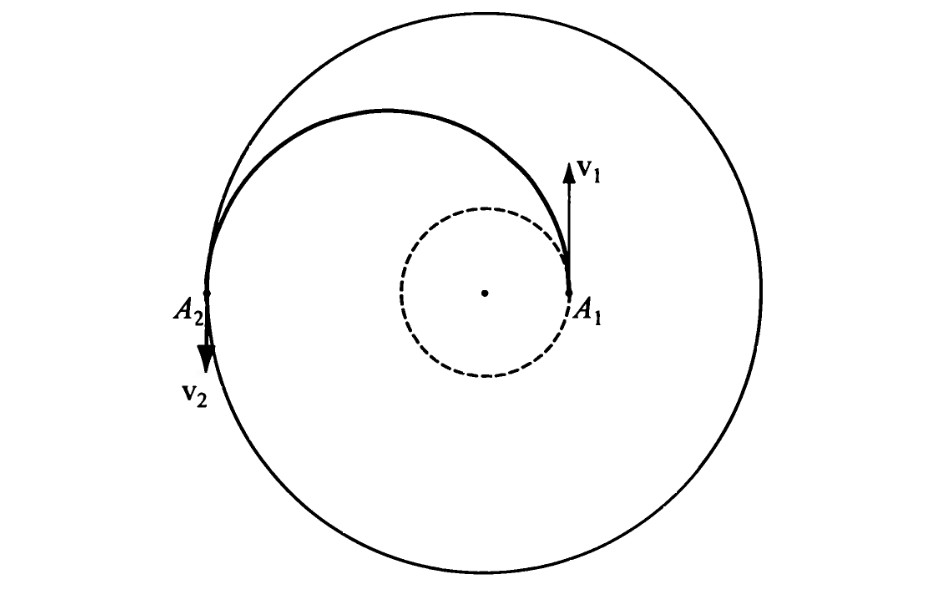
Рис.12

В космосе все движения обратимы. Точнее, если все скорости всех тел изменить на противоположные, то они будут двигаться по тем же орбитам, но в противоположную сторону. В частности, если все стрелки на рис.12 перевернуть, то получим тоже допустимые движения. Это значит, что оптимальный перелет с высокой на низкую орбиту — тот же эллипс Гомана-Цандера с теми же импульсами ?₂ и ?₁, но на этот раз не разгонными, а тормозными, в результате чего в дальнейшем можно ограничиться перелетами на более высокие орбиты.

Отнюдь не всегда начальная и конечная орбиты лежат в одной плоскости. Существенное изменение плоскости орбиты — задача, непосильная для современных ракет (опять космический парадокс: автомобилю трудно забираться на гору, но ничего не стоит свернуть направо). Действительно, чтобы повернуть плоскость орбиты на 60°, по правилу векторного сложения скоростей требуется импульс, равный скорости движения КА, т.е. 8 км/с для низких спутников Земли.

Но задача о стыковке двух ИСЗ решается и для совсем разных орбитальных плоскостей, лишь бы совпадали их наклоны к экватору. Действительно, плоскости орбит близкого и далекого ИСЗ из-за влияния сжатия Земли вращаются вокруг полярной оси и притом с разными угловыми скоростями. Достаточно выждать неделю-другую, пока плоскости орбит не совпадут, тогда и надо включать двигатели по описанной схеме.

Вернемся к задаче перелета между компланарными круговыми орбитами. А что, если не ограничиваться двумя импульсами? Как показал в тридцатых годах А.А. Штернфельд (родившийся в Польше, работавший сначала во Франции, затем в СССР), решение в этом случае зависит от отношения ? радиусов внешней и внутренней окружностей. Если 1<??11,9, то полуэллипс остается оптимальной траекторией. Если ??15,6, то более экономичен трехимпульсный перелет, осуществляемый по схеме типа Петербург-Одесса через Владивосток (рис.13). В точке А₁ дается разгонный импульс ?₁, больший, чем нужно для выхода на эллипс Гомана-Цандера, но меньший, чем нужно для ухода на бесконечность. В результате получим полуэллипс А₁А₂, заходящий за орбиту цели. В его апоцентре А₂ снова прикладывается разгонный импульс ?₂, обеспечивающий полет по полуэллипсу А₂А₃, касательному к орбите цели. В точке А₃ дается уже тормозной импульс ?₃, переводящий космический аппарат на круговую орбиту. И что удивительно: чем дальше расположена точка тем меньше характеристическая скорость ?₁+?₂+?₃. А оптимального перелета нет! Он существует лишь как некая абстракция: надо уйти в «бесконечность», приложить там «нулевой» импульс и вернуться в точку А₃.

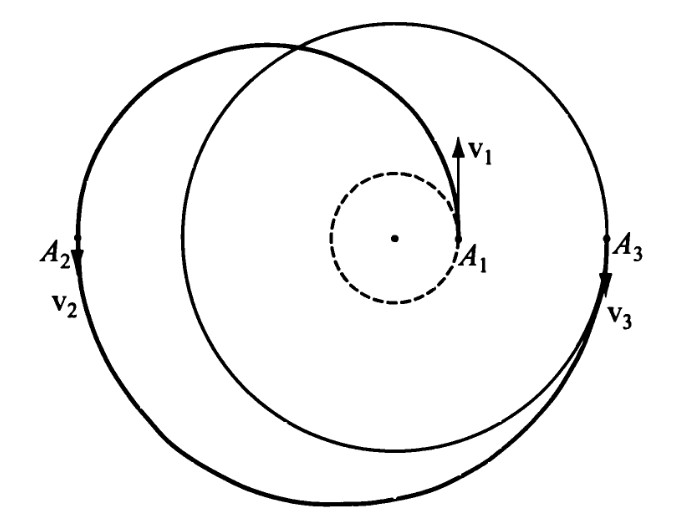
Рис.13

Если 11,9<?<15,6, то трехимпульсный переход по-прежнему экономичнее двухимпульсного, но только для достаточно удаленного расположения точки А₂. Если запретить далеко отрываться от родной Земли, то перелет Гомана-Цандера может все же оказаться оптимальным.

Перелеты Штернфельда — еще и средство изменения плоскости орбиты. Если точка А₂ расположена очень далеко, то импульс скорости ?₂ там очень мал. Его можно направить в любом направлении, затрачивая дополнительно совсем мало топлива, и получить орбиту желаемого наклона.

Покинем теперь околоземное пространство и устремимся к другим планетам. Как ни удивительно, ничего нового изобретать не придется. Достаточно в наших рассуждениях заменить Землю Солнцем, орбиту старта — орбитой Земли и орбиту финиша — орбитой планеты-цели. Правда, около самих планет надо учитывать их притяжение. Но зона, в которой это притяжение существенно (так называемая сфера влияния планеты), очень мала по сравнению с межпланетными расстояниями. Как применяется описанная теория в космонавтике? Почти каждая траектория перелета КА на околоземных орбитах или полет к Луне, Венере, Марсу представляет собой сокращенный эллипс Гомана-Цандера. Слово «сокращенный» означает, что радиус-вектор, соединяющий центральное тело и КА, поворачивается на угол, несколько меньший 180°. Так что траектория КА близка к оптимальной, но отличается от нее, причем почти всегда в одну сторону. Объясняется это тем, что мы учитывали до сих пор лишь один фактор — расход топлива. Но время перелета также играет не последнюю роль. Чем оно короче, тем лучше: меньше нужно запасать энергии для работы приборов, меньше вероятность выхода приборов из строя. А уж для пилотируемых полетов роль времени не нуждается в пояснении. Далее требуется уменьшить чувствительность к неизбежным неточностям при выведении на орбиту. А эллипс Гомана-Цандера к ним очень чуток. Немного не добрал скорость — и уже недолет. Все это и заставляет сокращать переходную орбиту.

А где же перелеты Штернфельда? В межпланетных полетах они вряд ли будут применяться. Они выгоднее двухимпульсных лишь для достижения Урана, Нептуна, Плутона и …Солнца. Но и прямой-то полет к внешним планетам требует десятков лет. А уж трехимпульсный перелет с вылетом из Солнечной системы займет сотни и тысячи лет. Недопустимо затянется и полет к Солнцу. Но не надо отчаиваться — мы расскажем о других путях достижения этой цели.

Радиус лунной орбиты содержит 60 радиусов Земли, так что ? значительно превышает предел 15,6. Полет к Луне через залунные области даст экономию около 8% топлива. Пока такая схема перелета не применялась: ведь время в пути — несколько месяцев вместо нескольких дней прямого полета. Но не исключено, что при освоении Луны для товарных ракетных поездов будет использоваться именно траектория Штернфельда. Сегодня же по подобным траекториям часто выводят на орбиту 24-часовые ИСЗ: это оптимальный способ получить высокую орбиту нулевого наклона при запуске с космодрома с широтой, превышающей 40°. Отметим очередной космический парадокс: легче вывести КА на орбиту Луны, чем на орбиту 24-часового ИСЗ, в 9 раз более близкую.