Книга: Солнечная система (Астрономия и астрофизика)

Движение ИСЗ

Как рассчитывают трассы небесных тел в сложных гравитационных полях? Простых формул, подобных выведенным Кеплером и Ньютоном для описания движения частицы вокруг шара, для сложных полей не существует. Более того, за редчайшими исключениями вообще не существует абсолютно точных формул. Это следствие реальной сложности движений. Какими же средствами располагает современная наука? В самых общих чертах их можно разделить на две группы.

1. Аналитические методы. С их помощью сложное движение можно представить как наложение бесконечного числа простых движений. До предела упрощенный пример — знакомая по школьным учебникам формула суммы бесконечного числа членов геометрической прогрессии

1/x=1+(1-x)+(1-x)²+(1-x)³+…     (9)

Предположим, что марсиане умеют складывать, вычитать и умножать числа, представленные десятичными дробями, и знают, что есть и обратное умножению действие — деление, но делить не научились. Так вот, левую часть (9) марсиане смогут вычислить, складывая большое количество чисел из правой части, а каждое из них получается умножением (1—х) самого на себя. Уже на этом простейшем примере видны две особенности аналитического подхода.

Во-первых, для получения точного ответа нужно проделать бесконечно много операций, что невозможно. Но для достижения заданной точности нужно произвести уже конечное число операций. Последнее тем больше, чем выше требования к точности. Пусть, например, х=1,1. Чтобы ошибка (9) составила не больше 0,01, следует взять два слагаемых справа; четыре слагаемых гарантируют погрешность менее 0,0001.

Во-вторых, формулы аналитического метода работают не для одного какого-то набора значений переменных величин, а для любых их значений из некоторой области. Так, равенство (9) можно применять не только при х=1,1, а для всех значений х от нуля до двух. Но для х=—1,5 формула (9) не годится и приходится прибегать к другим соотношениям. Напимер, для —2<х<0 можно применить формулу 1/х=—[1+(1+х)+(1+х)²+(1+х)³+…]. В небесной механике орбиты разного типа также описываются разным набором аналитических формул.

2. Численные методы представляют собой вычисление положения и скорости частицы в последовательные моменты, разделенные небольшими промежутками времени, по соответствующим значениям этих величин и действующих сил в предшествующие моменты. Такой путь прост и универсален. Большое количество вычислений в век электроники — недостаток не самый важный. Хуже, что получается лишь одна траектория и даже для соседней все вычисления приходится выполнять с самого начала.

На практике нередко комбинируют аналитический и численный методы, что привело к впечатляющим успехам в описании движения планет, их спутников, комет, астероидов. Но мы нарушим исторический порядок, обратившись сначала к искусственным небесным телам. ИСЗ ближе к нам и двигаются сравнительно просто. Естественно переходить от простого к сложному.

Свой виток вокруг планеты спутник проходит почти точно по эллипсу, но виток не замкнется. Следующий оборот будет отличаться от предыдущего примерно на 1/300, так как настолько притяжение Земли вблизи ее поверхности отличается от притяжения шара. За триста оборотов (примерно месяц для близких ИСЗ) орбита может измениться до неузнаваемости. Меняется не все. Истинное движение мало (в пределах 10км) отклоняется от движения по некоторому опорному эллипсу. Опорный эллипс имеет фиксированные размер, форму и наклон к плоскости экватора, но вращается вокруг двух осей одновременно. Во-первых, линия апсид (соединяющая перигей и апогей) поворачивается в плоскости эллипса с угловой скоростью ?₁. Во-вторых, сама эта плоскость поворачивается вокруг полярной оси с угловой скоростью ?₂. В терминах небесной механики перицентр испытывает вековое возмущение со скоростью ?₁ а восходящий узел орбиты на экваторе — вековое возмущение со скоростью ?₂. В результате траектория типичного ИСЗ приобретает вид запутанного клубка, изображенного на рис.8. Описанные свойства надо учитывать при проектировании, чтобы спутник с успехом выполнял свою работу.

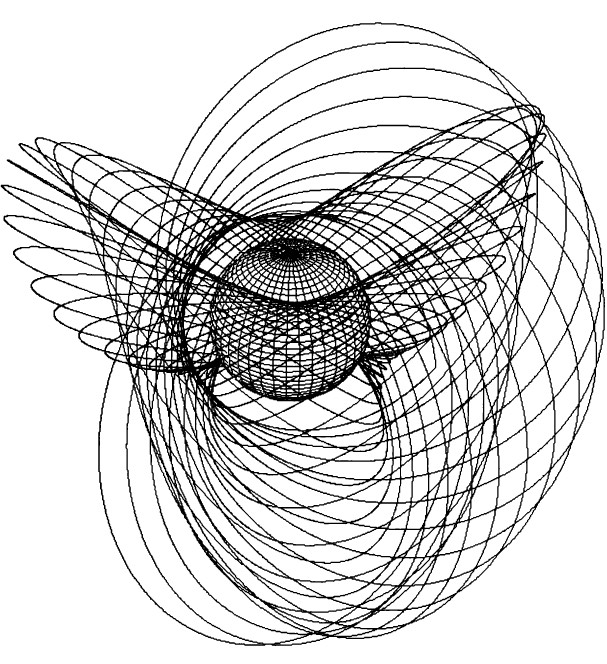
Рис.8

Возьмем для примера ИСЗ «Молния». Его основное назначение — осуществлять связь между западом и востоком России и СНГ. Следовательно, орбита должна быть достаточно высокой, чтобы сверху была видна значительная часть территории. Связь подчиняется суточному ритму (скажем, телепередача «Время» транслируется в одно и то же время в каждой зоне вещания), так что период ИСЗ обязан укладываться в сутках целое число раз. С учетом предыдущего условия получаем для периода одно из трех значений: 6, 8, 12 часов (особый случай 24 часов надо рассматривать отдельно). Наклон i плоскости орбиты к экватору должен лежать в пределах 40°?80° для покрытия широтной зоны, в которой расположен СНГ. Эксцентриситет следует взять близким к единице и направить апогей в Северное полушарие, тогда спутник будет почти все время в рабочей зоне, быстро пролетая Южное полушарие (вспомните о скоростях в разных точках эллипса). В результате отпадают периоды в 6 и 8 часов, так как для них эксцентриситет нельзя сделать большим, ведь внутри эллипса должна еще поместиться Земля с ее атмосферой. Остается период в 12 час.

Пока мы ограничивались рамками задачи одного притягивающего центра. Но «Молния» рассчитана на долгие годы работы, и выбранная орбита должна быть устойчивой на многих тысячах витков. Поэтому необходим учет несферичности Земли, что ставит под сомнение весь проект. Вращение линии апсид с угловой скоростью ?₁ через 180°/?₁ суток (если ?₁ измерять в градусах за сутки) повернет апогей в Южное полушарие, и наша «Молния» станет обслуживать Австралию. Однако величина ?₁, как показывают расчеты, содержит множитель (4—5sin²i) и обращается в нуль при i=63,4°. Такой наклон нас вполне устраивает. Реальные «Молнии» двигаются по орбитам с близким к указанному наклоном. Орбита «Молнии» (рис.9.) отличается от изображенной на рис.8. тем, что все апогейные точки располагаются на окружности, имеющей широту около 63°.

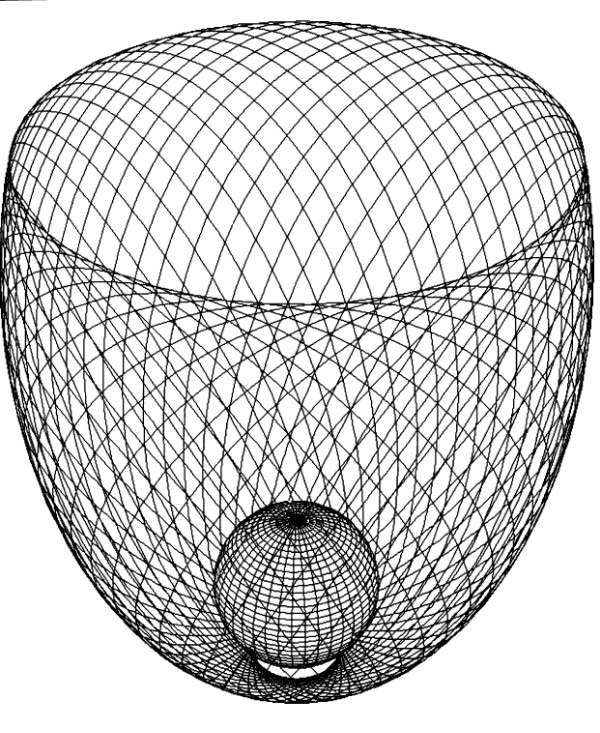
Рис.9

По рис.9 может показаться, что из-за вращения плоскости орбиты вокруг полярной оси территория России постепенно будет уплывать из-под орбиты «Молнии». Это, конечно, не так. На рисунке, в отличие от кино, не изобразить вращения планеты. Земля вертится, делая один оборот в то время, за которое спутник делает два оборота. Из двух витков «Молнии» лишь один — рабочий. Поэтому (хотя не только поэтому) надо иметь несколько таких спутников.

Обратимся к 24-часовым спутникам. Этот вариант активно используется в системах спутниковой связи многих стран — но только в круговом экваториальном варианте е?0, i?0. Для земного наблюдателя спутник на небе кажется неподвижным, «висящим» над одной и той же точкой земной поверхности. Влияние несферичности Земли, а также притяжение Луны и Солнца медленно уводит ИСЗ от «точки стояния», в результате чего приходится время от времени корректировать его орбиту.

Для спутников «Молния» выбраны орбиты, на которых ?₁=0. Активно используются в космонавтике и орбиты, на которых ?₂=0. Это полярные орбиты (i=90°), единственные, где спутник может быть виден в зените на полюсах.

Еще более интересен пример широко применяемых траекторий, для которых ?₂=0,986°/сут. Именно с такой угловой скоростью Земля обращается вокруг Солнца. Поэтому рассматриваемые орбиты называются солнечно-синхронными. Линия Солнце-Земля составляет с плоскостью орбиты постоянный угол. В частности, может совпадать с ней, вследствие чего спутник пролетает над каждым районом земной поверхности почти в одно и то же местное солнечное время. Это весьма удобно при сравнении фотоснимков, полученных в разные дни спутниками, исследующими Землю.