Книга: Солнечная система (Астрономия и астрофизика)

Пассивное движение в системе Земля-Луна

Пусть спутник Земли поднят так высоко, что может сближаться с Луной. В результате наложения земной и лунной гравитации разнообразие орбит становится поистине фантастическим. Никто пока не сумел перечислить все их типы. Рассмотрим один интересный класс замкнутых периодических орбит. Для простоты будем считать лунную орбиту окружностью.

Сначала надо ввести геоцентрическую систему отсчета, вращающуюся вместе с Луной. В этой системе Луна неподвижна, неподвижен и центр Земли, а сама Земля вращается с периодом в 24 ч. 50 мин. Этот период легко определит каждый из вас. В ясную лунную ночь отметьте положение тени какого-либо неподвижного предмета и засеките время. В следующую ясную ночь тень будет на том же месте через 24 ч. 50 мин. Введенная система отсчета кажется несколько искусственной. Но это не совсем справедливо. Такая система естественна для селенитов (воображаемых жителей Луны и будущих обитателей лунных баз). В их небе Солнце всходит и заходит. А Земля висит неподвижно, показывая одни и те же города каждые 24 ч. 50 мин. Здесь можно напомнить о том, что период вращения Земли вокруг оси равен 23 ч. 56 мин. Это звездные сутки. Для земного наблюдателя через это время каждая звезда возвращается на прежнее место, например, точно на небесный меридиан. Относительно Солнца период вращения Земли равен 24 ч. Это солнечные сутки. Наконец, относительно Луны — 24 ч. 50 мин. Этот период можно бы назвать лунными сутками Земли. Именно с таким периодом повторяются условия передач земных радиостанций для селенитов.

Периодические орбиты — это траектории, замыкающиеся в нашей вращающейся вместе с Луной системе отсчета после истечения некоторого периода Т. Простейшими периодическими орбитами будут положения равновесия. Ведь точечную траекторию можно считать периодической при произвольном периоде Т. Как показали Л. Эйлер и Ж. Лагранж, в нашей системе существует ровно пять положений равновесия, так называемых точек либрации L₁—L₅ (рис.10). Три из них, найденные Эйлером, лежат на прямой Земля-Луна. Одна из них, находящаяся между Землей и Луной точка либрации L₁, представляет и практический интерес. В будущем ее предполагается использовать как место перевалочной базы при освоении Луны. Точки либрации L₁, L₂, L₃ неустойчивы. Поэтому время от времени необходима незначительная коррекция космического аппарата (КА), находящегося в окрестности L₁, во избежание его ухода от L₁ на неприемлемое расстояние.

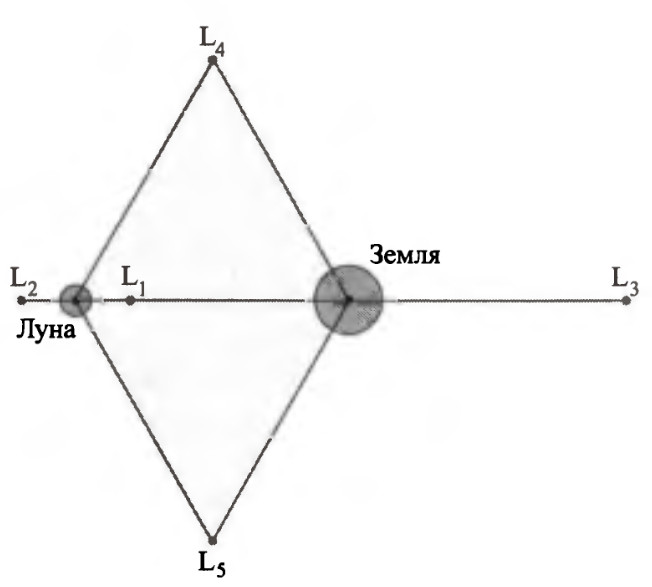
Рис.10

Не исключено и создание базы в одной из открытых Лагранжем точек L₄, L₅, лежащих в плоскости лунной орбиты и образующих вместе с Землей и Луной два равносторонних треугольника. Это тем заманчивее, что L₄ и L₅оказались устойчивыми, в отличие от L₁, L₂, L₃. Неучтенное притяжение Солнца все же может вывести КА из приемлемой окрестности L₄ или L₅. Так что коррекция орбиты может понадобиться и здесь, но гораздо реже.

Вокруг каждой из точек L₁—L₅ существуют и «настоящие» периодические орбиты. Траектории вокруг лежащей дальше Луны точки L₂, похожие на овал в плоскости, перпендикулярной прямой Земля-Луна, получили особое наименование гало-орбит. В будущем они сыграют важную роль в освоении Луны. На гало-орбитах разместятся спутники-ретрансляторы, позволяющие поддерживать радиосвязь между Землей и базой, расположенной на обратной стороне Луны.

На рис.11 изображена более замысловатая периодическая орбита, показывающая их богатое разнообразие. КА на такой орбите попеременно является то спутником Земли, то спутником Луны.

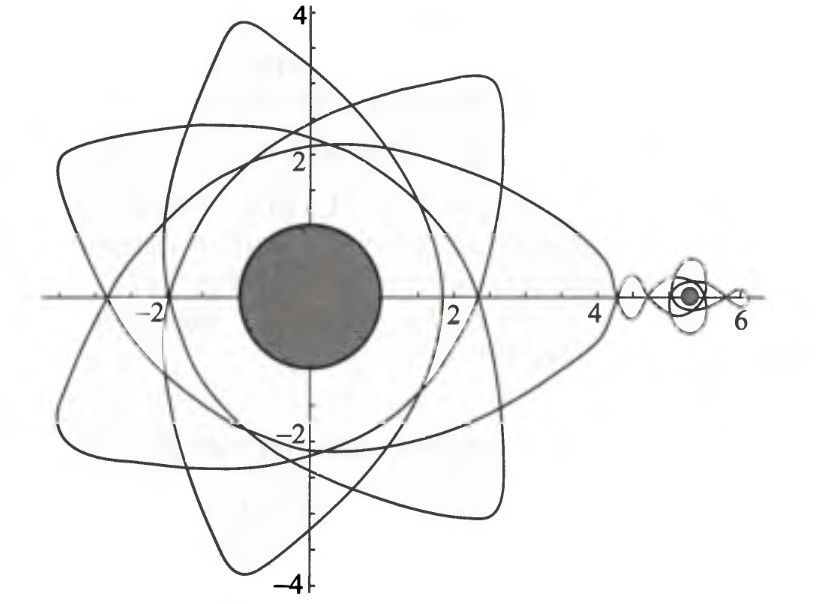
Рис.11

Задача о движении КА в гравитационном поле Земли и Солнца математически тождественна задаче о движении в поле Земли и Луны. Тут тоже существуют периодические орбиты и точки либрации. Более того, они уже используются на практике. Космический аппарат SOHO для исследования процессов на Солнце находится все время на гало-орбите вблизи точки L₁.

Решения задачи о движении объекта в окрестности двух массивных тел оказывается очень полезным, и не только в приложении к Солнечной системе: они используются и при изучении движения вещества в двойных звездных системах, и в звездных скоплениях, и в системах галактик. Но нужно помнить, что все эти полезные решения получены при определенных предположениях. Например, точки Лагранжа существуют в рамках ограниченной задачи: два тела имеют конечные массы (любые; обе массы могут быть даже равны друг другу), а третья бесконечно мала (у нас это космический аппарат). Движение в окрестности коллинеарных точек либрации L₁, L₂, L₃ всегда неустойчиво. Устойчивость движения в окрестности треугольных точек Лагранжа L₄, L₅ зависит от соотношения между массами основных тел. Обозначим массы основных тел через m₁?m₂. Введем безразмерный параметр µ, выражающий отношение этих масс:

µ=m₂/(m₁+m₂)

А.М. Ляпунов доказал, что движение в окрестности треугольных точек либрации устойчиво в первом приближении при 27µ(1—µ)<1, что равносильно условию

µ<µ₀=0,0385209.

Для системы Земля-Луна µ<(1/3)/µ₀, значит, треугольные точки либрации устойчивы (при отсутствии не учтенных в задаче возмущений!). А вот для системы Плутон-Харон µ>3,7µ0. Устойчивости нет. В системах двойных звезд, как правило, µ>µ₀ и движение неустойчиво.