Книга: Ритм Вселенной. Как из хаоса возникает порядок

Глава 7. Синхронизированный хаос

Глава 7. Синхронизированный хаос

Он не производил впечатления человека, совершившего революцию. Скромный мужчина невысокого роста, в возрасте примерно семидесяти лет и с несколько монотонной речью, Эд Лоренц не только внешностью, но и повадками был похож на типичного провинциала. Увидев его у стойки придорожного кафе где-нибудь в штате Мэн, вы наверняка приняли бы его за фермера. Я часто видел его во время обеда в кафетерии МТИ, что в Мемориале Пола Уолкера. Он входил в кафетерий своей слегка прихрамывающей походкой в сопровождении жены; они держали друг друга за руки, а в свободной руке у каждого из них была трость. Каждый год, когда я приступал к чтению студентам курса лекций по теории хаоса, мы проходили один и тот же ритуал; я настолько привык к нему, что в мельчайших подробностях рисовал его в своем воображении. Итак, я обязательно позвоню профессору Лоренцу и попрошу его прочитать моим студентам вступительную лекцию. Он, конечно же, изумится (между прочим, совершенно искренне) моему предложению и обязательно спросит: «О чем же я буду рассказывать им?» А я обязательно отвечу: «Надеюсь, вы не будете против рассказать им об уравнениях Лоренца?» Он уточнит: «О, вы имеете в виду эту маленькую модель?»[178] А затем – так же предсказуемо, как смена времен года – он появится в аудитории, охваченной благоговением, и расскажет студентам… Нет, вовсе не об уравнениях Лоренца, а о том, над чем он работает сейчас. В конце концов, не так уж важно, о чем именно он будет рассказывать. Присутствующие в аудитории собирались в ней хотя бы для того, чтобы взглянуть на творца современной теории хаоса[179].

«Эта маленькая модель», между прочим, совершила настоящий переворот в науке. В 1963 г., пытаясь уяснить непредсказуемость погоды, Лоренц составил систему из трех дифференциальных уравнений – нелинейных, но вовсе не таких ужасных на вид, какими они обычно бывают. Более того, математику или физику они могли показаться обманчиво простыми, похожими на стандартные примеры, которые можно найти в учебниках. Глядя на них, любой математик или физик мог подумать: «Пожалуй, я смог бы решить эту систему уравнений». Однако в том-то и дело, что не смог бы. Никто не смог бы. Решения уравнений Лоренца вели себя так, как не снилось ни одному математику. Его уравнения генерировали хаос: на первый взгляд, случайное, непредсказуемое поведение, управляемое неслучайными, детерминистскими законами.

Поначалу никто не обратил внимания на необычность уравнений Лоренца. Статья Лоренца «Детерминированный непериодический поток», затерявшаяся на страницах 130–141 журнала Journal of the Atmospheric Sciences, в течение первых десяти лет своего существования цитировалась примерно один раз за год. Но как только революция хаоса развернулась во всю свою мощь (а это случилось в 1970–1980-х годах), ссылки на «эту маленькую модель» посыпались как из рога изобилия.

Первая волна поднялась, когда некоторые ученые, представляющие разные области науки, пришли к пониманию того, что все они наблюдают проявления одного и того же таинственного феномена. Экологи обнаружили хаос в простой модели, описывающей динамику популяции диких животных. Вместо того чтобы выравниваться или циклически повторяться, моделируемая популяция неожиданно разрослась и неравномерно распалась на протяжении жизни буквально двух поколений, хотя в самой модели не было заложено ничего случайного. Астрономы были озадачены результатами измерений вращательного движения Гипериона[180], небольшой картофелеобразного спутника Сатурна: вместо того чтобы вращаться вокруг собственной оси, подобно большинству планет-спутников, он хаотично шатался и кувыркался, как пьяный. Физики отвлеклись на какое-то время от размышлений над кварками и черными дырами и решили уделить внимание более прозаическим феноменам, к которым они прежде относились как к досадным помехам: прерывистым пульсациям неустойчивых лазерных лучей, хаотическим колебаниям напряжения в некоторых электрических цепях и даже протекающим водопроводным кранам. Всем этим явлениям, как оказалось, предстояло играть роль символов хаоса. По иронии судьбы, ряду «чистых» математиков, начиная с Анри Пуанкаре, уже примерно 70 лет было известно о хаосе, но почти никому, кроме них самих, не был понятен ни их особый жаргон, ни их математические абстракции, поэтому их идеи оказывали лишь весьма незначительное влияние за пределами узкого круга посвященных.

Все перечисленное выше представляет собой типичные препятствия, возникающие на пути развития любой междисциплинарной науки. Большинство ученых чувствуют себя весьма комфортно в своих узких научных областях, отгородившись от своих интеллектуальных соседей языковыми барьерами, своими особыми научными пристрастиями и спецификой своей научной культуры. Однако все это не было присуще Лоренцу. По специальности он был метеорологом, однако его первой любовью была математика. Людей, подобных Лоренцу, можно найти в любой научной области; в своих научных сообществах такие люди кажутся белыми воронами. Все эти люди хорошо чувствуют динамику, поток, общую картину, скрытые закономерности и симметрии. Особенно притягателен для них самый темный и непознанный угол теоретической науки: царство нелинейных проблем.

Математик Станислав Улам однажды сказал, что назвать какую-либо проблему нелинейной – все равно что сходить в зоопарк и рассказать обо всех интересных животных, которых вы там увидели, за исключением слона. Тем самым Улам хотел подчеркнуть, что большинство животных не являются слонами, а большинство уравнений нелинейны. Линейные уравнения описывают простые, идеализированные ситуации, когда причины пропорциональны следствиям, а прилагаемые силы пропорциональны реакциям, то есть противодействиям. Если вы согнете стальной стержень не на один миллиметр, а на два, то сила, с которой он пытается распрямиться, окажется в два раза большей. Определение «линейное» означает именно эту пропорциональность: если вы изобразите график зависимости отклонения стержня от прилагаемой силы, то этот график будет представлять собой прямую линию. (В данном случае определение «линейное» не означает последовательное, когда мы имеем в виду пошаговое продвижение вперед или когда мы говорим о «линейном мышлении», под которым подразумевается однонаправленное мышление, также являющееся, в некотором роде, пошаговым мышлением. То есть речь идет о разном использовании одного и того же слова.)

Линейные уравнения поддаются решению в силу своей модульной структуры: их можно расчленить на составные части. Каждую такую часть можно анализировать и решать по отдельности, а в конце все отдельные ответы можно воссоединить – в буквальном смысле, снова сложить между собой – и получить таким образом правильный ответ для исходной задачи. В линейной системе целое в точности равняется сумме его составных частей.

Однако линейность зачастую является лишь аппроксимацией некой более сложной реальности. Большинство систем ведут себя линейно, лишь когда они близки к состоянию равновесия и лишь когда мы не оказываем на них слишком сильных воздействий. Инженер-строитель может предсказать, как будет раскачиваться многоэтажный дом под напором ветра, если сила ветра не окажется слишком большой. Электрические цепи ведут себя совершенно предсказуемо – пока в цепи не случится скачок напряжения или тока. Когда какая-либо система становится нелинейной, будучи выведена из своего обычного режима работы, она начинает вести себя непредсказуемо. В таком случае обычные, линейные уравнения, которыми описывается поведение системы, уже неприменимы.

Тем не менее у вас не должно сложиться впечатление, будто нелинейность сама по себе опасна или даже нежелательна. Более того, наша жизнь зависит от нелинейности. В любой ситуации, когда целое не равно сумме его составных частей, когда мы имеем дело с сотрудничеством или конкуренцией составных частей, а не просто с суммированием их влияний, можно быть уверенным, что мы имеем дело с проявлениями нелинейности. В биологии нелинейность наблюдается повсеместно. Наша нервная система состоит из нелинейных компонентов. Экология подчиняется нелинейным законам (в той мере, в какой они известны нам). Комбинированная терапия, которую применяют к больным СПИДом (так называемые лекарственные коктейли), эффективны именно в силу нелинейности иммунной реакции и динамики вирусной популяции: сочетание из трех лекарств оказывается гораздо более действенным, чем суммарное воздействие трех этих лекарств, если пациент принимает их по отдельности. Что же касается человеческой психологии, то она носит абсолютно нелинейный характер. Например, если вы прослушаете две свои любимые песни одновременно, то вряд ли вы получите двойное удовольствие.

Именно этот синергетический[181] характер нелинейных систем чрезвычайно затрудняет их анализ. Такие системы невозможно расчленить на составляющие, чтобы проанализировать их по отдельности. Их приходится анализировать в целом, как когерентный объект. Как указывалось выше, такая необходимость глобального мышления является самой серьезной проблемой в уяснении того, как большие системы осцилляторов могут самопроизвольно синхронизироваться. Вообще говоря, все, что касается самоорганизации, нелинейно в принципе. Поэтому изучение синхронизма всегда неразрывно связано с изучением нелинейности.

Именно синергетический характер нелинейных систем делает их столь богатыми. Каждая из крупных нерешенных проблем в науке, начиная с природы сознания и заканчивая раком и коллективным помешательством экономики, является нелинейной. На протяжении нескольких следующих столетий наука будет биться над решением нелинейных проблем. Начиная с 1960-х и 1970-х годов все первопроходцы синхронизма – я имею в виду таких ученых, как Винер, Уинфри, Курамото, Пескин и Джозефсон, – уже прокладывали путь к этой неизведанной научной вершине, пытаясь уяснить причины самопроизвольного возникновения порядка в системах, состоящих из огромного числа осцилляторов. С возникновением теории хаоса ряды этих первопроходцев пополнились целой армией новых энтузиастов, устремившихся к той же вершине, но выбравших для этого другой путь.

Нелинейные проблемы всегда были трудны для понимания. Именно поэтому успех Лоренца в решении проблемы хаоса так вдохновил ученых. Внезапно стало очевидно, что даже простейшие нелинейные системы могут демонстрировать очень сложное поведение – гораздо более сложное, чем можно было ожидать. Такой вывод мог бы показаться пессимистическим, однако он породил надежду, что какие-то, на первый взгляд случайные, явления могут таить в себе некие скрытые закономерности.

Затем настал черед второй волны теории хаоса, которая выявила, что сам по себе хаос, вопреки собственному названию, заключает в себе новый, замечательный вид порядка. Это выдающееся открытие совершил физик Митчел Фейгенбаум, который показал, что существуют определенные универсальные законы, управляющие переходом от регулярного поведения к хаотическому. Грубо говоря, совершенно разные системы могут абсолютно одинаково становиться хаотическими. Прогнозы, сделанные Фейгенбаумом, были вскоре подтверждены в результате экспериментов с электроными цепями, закручивающимися потоками, химическими реакциями, полупроводниками и сердечными клетками. Казалось, сбывается старая пифагорова мечта: окружающий нас мир состоит не из земли, воздуха, огня и воды, а из чисел. Законы Фейгенбаума вышли за рамки поверхностных различий между сердечными клетками и кремниевыми полупроводниками. Разные материалы – одни и те же законы хаоса. Вскоре ученым предстояло открыть другие универсальные законы. Казалось, выход из тупика найден.

Для науки о нелинейных процессах наступило время эйфории. Хаос… Это слово само по себе звучит таинственно. Кое-кто рекламировал эту область науки как третью великую революцию в физике XX столетия, наряду с теорией относительности и квантовой механикой. Впервые она позволила разгадать некоторые из загадок нелинейности и установила связи между областями, которые ранее считались не связанными между собой. Книга Джеймса Глейка Chaos, опубликованная в 1987 г. и ставшая бестселлером, познакомила широкие массы читателей с теорией хаоса и с биографиями таких колоритных личностей, как Лоренц и Фейгенбаум, научный гений и заядлый курильщик с бетховенской шевелюрой, предпочитающий прогуливаться улицами Лос-Аламоса глубокой ночью и пытающийся раскрыть тайну турбулентности. А когда Джефф Голдблюм сыграл роль специалиста по теории хаоса в «Парке юрского периода», затянутого в кожу и похожего на рок-звезду, хаос действительно наступил – особенно после того как он продемонстрировал эффект бабочки на руке Лоры Дем.

Эффект бабочки[182] стал самым известным символом этой новой науки – и это вполне объяснимо, поскольку он наиболее ярко демонстрирует сущность хаоса. Словосочетание «эффект бабочки» было заимствовано из заголовка статьи Лоренца, опубликованной в 1979 г. Статья называлась «Предсказуемость: может ли взмах крыльев бабочки в Бразилии вызвать торнадо в Техасе?». Идея заключается в том, что в любой хаотической системе даже небольшие возмущения нарастают с высокой скоростью, по экспоненциальному закону, что обусловливает невозможность долгосрочных прогнозов.

Печальный вывод из эффекта бабочки заключался в том, что две хаотические системы никогда не смогут синхронизироваться между собой (по крайней мере очень многие были склонны так думать). Даже если вы очень постараетесь одинаково запустить в действие эти две хаотические системы, их начальные состояния все равно будут различаться между собой, пусть и на бесконечно малую величину. В регулярных системах столь незначительная разница оставалась бы такой же незначительной в течение долгого времени, но в хаотической системе расхождение нарастает и запитывается от самого себя настолько быстро, что системы рассинхронизируются практически мгновенно. Казалось, что две самые актуальные отрасли науки о нелинейности – хаос и синхронизм – никогда не пересекутся между собой. Казалось, что они фундаментально несовместимы.

Утверждение о невозможности синхронизированного хаоса, каким бы убедительным оно ни казалось, в наши дни считается ошибочным. Хаос можно синхронизировать.

Это интереснейшее явление было открыто в начале 1990-х годов, что повлекло за собой изменение представлений о самом хаосе. Традиционно хаос рассматривался как досадная помеха, что-то такое, от чего нужно избавиться теми или иными способами. Позднее, на пике революции в науке, хаос стал знаменитой диковиной. Его повсеместность в природе получила признание; была выявлена его скрытая упорядоченность. Никто не знал, можно ли его приспособить для чего-либо, однако это было не так уж важно. Он был замечателен сам по себе. Теперь, с открытием синхронизированного хаоса, ситуация вновь поменялась. В одночасье хаос показал, что может быть полезен[183]. Физики и инженеры мечтали о способах, с помощью которых им удастся использовать его замечательные свойства на практике, например шифровать звонки по мобильному телефону и через другие беспроводные формы связи, чтобы посторонние лица не могли прослушивать их.

Открытие синхронизированного хаоса расширило также наше понимание самого синхронизма. В прошлом синхронизм всегда ассоциировался с ритмичностью. Эти две концепции настолько тесно связаны между собой, что можно легко упустить важную разницу между ними. Ритмичность означает, что нечто повтояет свое поведение через регулярные промежутки времени; синхронизм означает, что два процесса протекают одновременно. Путаница возникает потому, что многие синхронные явления не только синхронны, но и ритмичны. Синхронные светлячки не только мерцают в унисон – они мерцают периодически, через определенные интервалы времени. Клетки-ритмоводители сердца запускаются синхронно и с постоянной частотой. Луна поворачивается вокруг собственной оси один раз за то время, пока она совершает один полный оборот вокруг Земли; и ее вращение вокруг собственной оси, и ее вращение вокруг Земли следует циклам, которые регулярно повторяются.

Однако нам известно, что, по крайней мере в принципе, синхронизм может поддерживаться и в отсутствие периодичности. Вспомните о музыкантах в оркестре. Все скрипки вступают одновременно и все время поддерживают синхронизм своих действий. Однако исполняемая ими музыка вовсе не периодична: они не повторяют все время один и тот же музыкальный пассаж. Можно вспомнить и об участниках соревнований по фигурному катанию, в частности о выступлениях спортивных пар. Свои грациозные движения они совершают в тандеме, однако этим движениям отнюдь не присуща периодическая повторяемость.

Эти проявления синхронизма в отсутствие периодичности производят на нас сильное впечатление, они восхищают нас, иногда даже заставляют нас вскакивать с места. Складывается впечатление, что для этого необходимы ум и артистичность; именно поэтому открытие синхронизированного хаоса произвело на ученых столь ошеломляющее впечатление: оно продемонстрировало, что даже неодушевленные объекты способны обеспечить примитивную версию такого же «трюка». Чисто механические системы могут вести себя непредсказуемо, поддерживая в то же время идеальный синхронизм.

Чтобы понять, как работает синхронизированный хаос, нужно сначала уяснить, что представляет собою сам хаос. К сожалению, у многих из нас успели сложиться неправильные представления о хаосе. (Между прочим, это утверждение не относится к периодичности. Мы инстинктивно понимаем ее правильно. Все циклы вокруг нас – сокращения сердечной мышцы, тиканье настенных часов, смена времен года, нестерпимое бип-бип-бип грузовика, дающего задний ход – позволяют составить точное представление о подлинном значении периодичности в нашей жизни. Вы можете даже ощущать у себя внизу живота ритмичное буханье барабана, когда мимо вас марширует военный оркестр. Теперь нам нужно выработать у себя такое же внутреннее, инстинктивное ощущение хаоса.)

Частично эта путаница объясняется самим словом хаос. В обыденном смысле хаос означает совершенный беспорядок. Однако в техническом смысле хаос означает состояние, которое лишь кажется случайным, но на самом деле порождается неслучайными законами. Как таковой, хаос занимает некое промежуточное (и малоизученное) положение между порядком и беспорядком. Он кажется непредсказуемым лишь на первый взгляд, поскольку в действительности он содержит в себе зашифрованные закономерности и подчиняется жестким правилам. Он достаточно предсказуем на коротком отрезке времени, но непредсказуем на длительном. К тому же он никогда не повторяется: его поведение носит непериодический характер.

Например, хаос, описываемый уравнениями Лоренца, наглядно иллюстрируется хитроумным изобретением, странным и в то же время прекрасным – настольным водяным колесом[184], сконструированным Виллемом Малкусом, одним из бывших коллег Лоренца в МТИ. Оно предназначалось для использования в качестве учебного пособия, которое должно было дать студентам общее представление о хаосе в действии. Первоначальный вариант такого пособия, сконструированный Малкусом и его коллегой Лу Ховардом, представлял собой вращающийся деревянный диск, к ободу которого была прикреплена примерно дюжина протекающих бумажных стаканчиков (что-то наподобие кресел на «чертовом колесе»). Как рассказывал мне Малкус, этот прототип был довольно «топорной работой»: когда в стаканчики заливалась вода, чтобы привести все колесо в движение, вода просачивалась сквозь стаканчики и выливалась на стол и пол.

Малкус усовершенствовал свое водяное колесо. В результате усовершенствования оно превратилось в полностью автономный механизм.

Пластиковое колесо диаметром около одного фута вращается в плоскости, слегка наклоненной по отношению к горизонту (в отличие от обычного водяного колеса, которое вращается в вертикальной плоскости). При нажатии на переключатель вода автоматически подкачивается в подвесной коллектор (перфорированный рукав), а затем выпускается через десятки маленьких отверстий в раздельные камеры, расположенные по периметру колеса (аналог бумажных стаканчиков в первоначальной версии). В нижней части каждой такой камеры вода просачивается через микроканал и собирается в резервуаре, помещенном под колесом, откуда она закачивается обратно через упомянутые выше отверстия. Такая схема рециркуляции обеспечивает устойчивый приток воды.

При включении этого агрегата поначалу не происходит ничего примечательного. Колесо остается неподвижным. По мере заполнения камер вода издает приятные булькающие звуки; между тем вода из камер понемногу просачивается (правда, просачивание происходит медленнее, чем наполнение камер). Как только камеры оказываются заполненными до предела, колесо становится неустойчивым (верхняя часть перевешивает) и начинает качаться (поворачиваться) в одном направлении подобно маятнику, который был поднят вертикально вверх, а затем отпущен. Этот поворот приводит к тому, что под отверстиями коллектора оказывается новая совокупность камер, а камеры, заполненные водой, автоматически выводятся из-под отверстий коллектора. Вскоре у вас создается ощущение, что вы наблюдаете определеную закономерность: колесо постоянно поворачивается в одном направлении (например, против часовой стрелки). Однако через какое-то время эти повороты становятся все более замедленными (колесо словно из последних сил совершает свой очередной поворот), по мере того как колесо становится все более разбалансированным в результате несимметричного размещения воды по его периметру. Наконец, колесо, пытаясь совершить свой последний поворот, останавливается, после чего начинает двигаться в противоположном направлении, на сей раз поворачиваясь по часовой стрелке. Еще через какое-то время в поведении колеса вырисовывается определенная картина: бессистемная, случайная последовательность вращений то по часовой стрелке, то против, совершаемых в непредсказуемые моменты времени. Например, колесо может повернуться три раза по часовой стрелке, затем один раз против, затем четыре раза по часовой стрелке, после чего семь раз против часовой стрелки и т. д. Это движение никогда не затухает и никогда не повторяется.

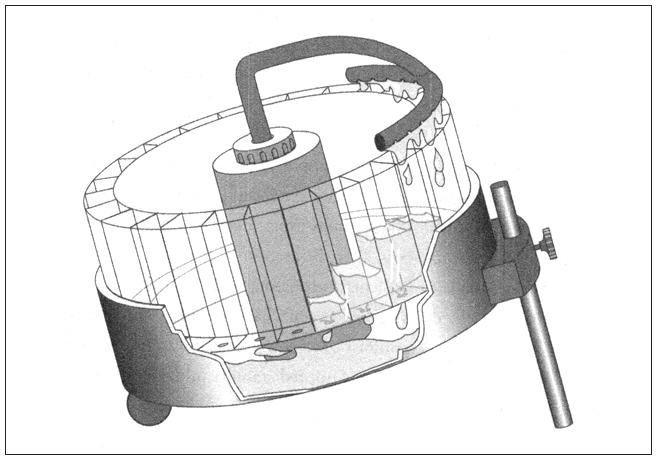
Самое удивительное здесь заключается в том, что вращение колеса носит совершенно случайный, непредсказуемый характер, несмотря на то что в самом механизме, который приводит в движение это колесо, нет ничего случайного и непредсказуемого. Вода подается в него с постоянной скоростью. Тем не менее складывается впечатление, будто колесо не может выбрать для себя какое-то определенное поведение, и поэтому начинает вести себя бессистемно. Более того, его поведение невозможно воспроизвести, повторить. Когда вы в следующий раз запустите это колесо, картина его вращений окажется другой. Как бы вы ни старались обеспечить неизменность исходных условий от одного запуска к другому, в лучшем случае колесо будет повторять картину своего поведения лишь в течение короткого времени, а затем станет отклоняться от нее все больше и больше, и в конечном счете у этой картины уже не останется ничего общего с предыдущим поведением колеса.

Разумеется, если бы вам удалось создать абсолютно идентичные начальные условия, то колесо в точности воспроизводило бы свое предыдущее поведение. В этом, собственно говоря, и заключается сущность детерминистского подхода: текущее состояние единственным образом определяет будущее состояние. Движением колеса управляют детерминированные уравнения – ньютоновские законы движения и законы механики жидкостей, – поэтому, в принципе, если вам известны вначале все переменные, вы можете предсказать будущее движение колеса. Сами по себе эти уравнения не содержат шума, элементов случайности или каких-либо других источников неопределенности. К тому же, если вы решаете эти уравнения на компьютере, используя одни те же начальные значения для всех переменных, то во всех случаях предсказанный исход будет одним и тем же. В этом смысле все можно воспроизвести и повторить.

Однако в реальном, а не компьютерном, мире переменные от случая к случаю не повторяются в точности. Даже микроскопической разницы – лишней капли воды в какой-либо из камер, оставшейся от предыдущего эксперимента, или колебания воздуха в результате выдоха, совершенного кем-либо из взволнованных наблюдателей, – будет достаточно для того, чтобы изменить движение колеса; поначалу это изменение будет незаметным, но уже очень скоро оно приведет к непредсказуемым последствиям.

Таким образом, характерные особенности хаоса таковы: бессистемное и случайное, на первый взгляд, поведение системы, которая во всех остальных отношениях является детерминированной; предсказуемость на коротком отрезке времени вследствие действия детерминистских законов; и непредсказуемость на продолжительном отрезке времени вследствие действия упоминавшегося выше «эффекта бабочки».

Феномен хаоса порождает ряд философских вопросов, которые могут поставить в тупик человека, не привыкшего задумываться над ними. Например, некоторые из моих студентов слишком легкомысленно относятся к «эффекту бабочки», считая его очевидным и не заслуживающим особого внимания. Всем нам известно, что даже какая-нибудь «мелочь» способна оказать огромное влияние на всю нашу жизнь и даже на жизнь целой страны. Учитывая огромную сложность мира, в котором мы живем, и огромное количество переменных (о существовании многих из которых мы даже не подозреваем, а если даже нам известно об их существовании, то далеко не всегда мы оказываемся в состоянии правильно оценить их влияние), которые оказывают влияние на нашу жизнь, неудивительно, что даже малозначительные, на первый взгляд, события подчас бывают способны инициировать совершенно непропорциональные по своим масштабам цепные реакции. Вспомните старое стихотворение о разбитой армии.

Однако до появления теории хаоса лишь очень немногие из нас понимали, что подобные каскады событий могут влиять даже на простейшие системы: водяные колеса и кувыркающиеся планеты, протекающие водопроводные вентили и механические системы, для которых известны все законы и которые характеризуются буквально несколькими переменными. Однако даже в таких простых системах скрываются зачатки хаоса; они еще не успели проявить себя, однако готовы в любой момент сделать это и преподнести нам немало сюрпризов.

Еще один нюанс: в хаосе любая точка является точкой нестабильности. Это даже хуже, чем затруднительное положение, в котором оказался путешественник в стихотворении Роберта Фроста «Другая дорога»; жизнь, которая подчиняется законам хаоса, еще более непредсказуема[187]. Каждый момент такой жизни является моментом истины. Каждое принимаемое решение имело бы долговременные последствия, которые изменяли бы вашу жизнь до неузнаваемости. Застегните пуговицы своей рубашки не сверху вниз, а снизу вверх – и вы даже не представляете, насколько по-другому может сложиться ваша жизнь через несколько лет. (Это вовсе не преувеличение. Дело в том, что в своей повседневной жизни мы привыкли двигаться по определенным траекториям; между тем мы не имеем ни малейшего представления о том, как сложится наша судьба, если мы начнем двигаться по непривычным для себя траекториям. Но чтобы не повредиться рассудком, человек вынужден исходить из того, что любые мелкие нестандартные решения, принимаемые им, не повлекут за собой сколь-нибудь существенных последствий для него. Эта дилемма была исследована в фильме «Осторожно! Двери закрываются» (Sliding doors). В этом фильме представлены две принципиально разные версии жизни одной женщины в зависимости от того, успела ли она заскочить в вагон метро, перед тем как закрылись его двери.)

В отличие от хаотических систем, ритмические системы не демонстрируют столь высокой чувствительности к слабым возмущениям. Щелкните пальцем по метроному – и он на мгновение остановится, а затем возобновит свои неумолимые тик-так. Он, конечно, собьется с первоначального ритма, но образовавшееся отклонение не будет нарастать с течением времени. Этот феномен можно представить более отчетливо, если мы вообразим два идентичных метронома, которые поначалу работали синхронно. Ударьте слегка пальцем один из них; после того как он возобновит ход, он начнет отставать от другого метронома на некий фиксированный интервал времени, причем это отставание не будет нарастать с течением времени. Вообще говоря, если слегка воздействовать на какую-либо нехаотическую систему, то это воздействие либо совсем не будет нарастать, либо будет нарастать очень умеренно, причем это нарастание будет пропорционально времени, которое прошло с момента воздействия. В таких случаях говорят, что ошибки нарастают во времени не быстрее, чем по линейному закону.

Важным моментом здесь является количественный момент. Линейный рост ошибок предполагает, что нехаотические системы ведут себя предсказуемо, по крайней мере в принципе. Приливы и отливы, возвращение кометы Галлея, моменты наступления затмений – все эти явления строго ритмичны и, следовательно, предсказуемы, поскольку слабые возмущения не перерастают со временем в большие ошибки прогнозирования. Чтобы предсказать поведение нехаотической системы на вдвое более продолжительном отрезке времени, вы должны в два раза точнее измерить ее начальное состояние. Чтобы ваш прогноз распространялся на отрезок времени, втрое более продолжительный, вы должны измерить начальное состояние системы в три раза точнее. Иными словами, горизонт предсказуемости также увеличивается по линейному закону, то есть прямо пропорционально точности, с которой определяется начальное состояние системы.

Хаотические системы, однако, ведут себя совершенно по-другому. Именно в хаотических системах мы начинаем ощущать по-настоящему деморализующие последствия «эффекта бабочки». Протяженность времени, которое может охватывать более или менее точный прогноз состояния хаотической системы, зависит от трех факторов: допустимой погрешности нашего прогноза, точности измерения исходного состояния хаотической системы и неподконтрольного нам масштаба времени, называемого временем Ляпунова[188][189], которое зависит от динамики, внутренне присущей самой этой системе.

Грубо говоря, наш прогноз может охватывать лишь время, соизмеримое с временем Ляпунова; после этого ошибки измерения истинного исходного состояния разрастаются до такой степени, что превышают допустимый порог погрешности. Снижая используемые стандарты или повышая точность измерения исходного состояния, мы всегда можем охватить своим прогнозом более продолжительные интервалы времени. Однако проблема заключается в жесткой зависимости «горизонта предсказуемости» от точности измерения исходного состояния: если вы хотите увеличить горизонт предсказуемости в два раза, не потеряв при этом в точности, то усилия, которые вам придется затратить для этого, должны возрасти не в два, а в десять раз. Если же вы ставите перед собой еще более амбициозные цели и хотите увеличить горизонт предсказуемости в три раза (при сохранении той же точности), то усилия, которые вам придется затратить для этого, возрастут в сто раз; четырехкратное увеличение горизонта предсказуемости будет стоить вам тысячекратных усилий и т. д. В любой хаотической системе требуемая точность начального измерения возрастает по экспоненциальному, а не линейному закону.

Необходимость выполнения подобного условия не внушает оптимизма. На практике это означает, что ваш горизонт предсказуемости вряд ли удастся сделать большим, чем n, умноженное на время Ляпунова, причем n должно быть очень малым числом. В данном случае точность ваших измерительных приборов не имеет значения. Время Ляпунова задает горизонт, за пределами которого приемлемое предсказание становится невозможным. В случае хаотической электрической цепи такой горизонт составляет примерно тысячную долю секунды; когда речь идет о прогнозах погоды, точную величину горизонта указать невозможно, но примерно он может равняться двум-трем дням; а в случае Солнечной системы он составляет пять миллионов лет.

Столь внушительная протяженность горизонта в случае Солнечной системы[190] обусловливает то, что сегодня мы можем с высокой точностью предсказывать движения планет; в масштабах человеческой жизни или даже истории астрономии в целом эти движения действительно предсказуемы. Когда мы вычисляем, какими были относительные положения планет сто лет назад или какими они будут через сто лет, наши предсказания вполне достоверны. Однако у нас нет никаких оснований доверять прогнозам, касающимся относительного положения планет 4 миллиарда лет тому назад, в момент зарождения жизни на Земле.

Последним нюансом, касающимся хаоса, является странный вид порядка, скрывающегося за этим хаосом. Хаос не есть нечто бесформенное (вопреки, как было сказано выше, обыденному смыслу этого слова). Скрытый смысл структуры, лежащей в основе хаоса, проявляется в работе действующего макета водяного колеса с его бесконечной последовательностью вращений то в ту, то в другую сторону; несмотря на то что эта последовательность никогда не повторяется в деталях, в целом ее характер остается одним и тем же. В хаосе заложена некая сущность – качество, которое никогда не изменяется.

Когда в начале 1960-х годов Лоренц анализировал свою «маленькую модель», ему удалось силой собственного воображения уловить сущность подлинного хаоса. Он принимал вид некой геометрической фигуры, чего-то необычного, не вполне поверхности, но и не твердого тела, имеющего четкие очертания. Задолго до появления современной компьютерной графики такую фигуру было не так-то просто воспроизвести и визуализировать. Даже после того как Лоренц нарисовал ее в собственном воображении, ему было очень трудно подобрать слова, чтобы передать ее необычную геометрию. Он описывал ее как «бесконечное сочетание поверхностей». В наши дни это получило название «странного аттрактора»[191][192].

Точно так же как окружность является формой периодичности, странный аттрактор является формой хаоса. Он пребывает в неком абстрактном математическом пространстве, называемом пространством состояний, координатные оси которого представляют все переменные в некой физической системе. Уравнения Лоренца содержали три переменные, поэтому его пространство состояний является трехмерным. В случае водяного колеса – точного механического аналога уравнений Лоренца – одна из переменных говорит нам о том, как быстро и в каком направлении вращается это колесо, тогда как две другие переменные характерихуют два конкретных аспекта того, как распределяется вода по периметру колеса. Значения этих переменных в тот или иной момент определяют конкретную точку в пространстве состояний, соответствующую «фотографии» данной системы в этот момент времени.

В следующий момент состояние системы изменится в результате поворота колеса, а также вытекания и перераспределения воды. Увлекаемая своей собственной динамикой, система действует, переходя из состояния в состояние. Подобно схемам в уроках танцев Артура Мюррея, уравнения Лоренца – это правила, описывающие каждый ваш следующий шаг. Они определяют бесконечно малые стрелки в каждой точке пространства состояний. В какой бы точке ни оказывалось состояние системы, оно должно следовать за стрелкой в данной точке; эта стрелка сразу же переводит систему в следующую точку, где этот процесс повторяется, и т. д. Время идет, и значения переменных изменяются, точка перемещается в пространстве состояний, прочерчивая непрерывный путь, называемый траекторией, и летит, подобно комете в вымышленном мире, который существует лишь в воображении математика. Прелесть этой идеи заключается в том, что она трансформирует динамику в геометрию. Хаотическое движение становится некой картиной – чем-то таким, что мы можем увидеть, статическим образом, который мы можем рассматривать и изучать.

На что же похож хаос? Упомянутая нами траектория бесконечно долго бороздит просторы пространства состояний. Она никогда не завершается и не пересекает сама себя, поскольку хаос никогда не повторяется. Лоренцу удалось доказать, что его траектория никогда не выходит за пределы определенной большой сферы, поэтому она никогда не может уйти в бесконечность. Замкнутая внутри этой сферы, приговоренная бесконечно долго блуждать внутри нее, ни разу не пересекаясь сама с собой, эта траектория должна следовать очень сложным путем. Возникает соблазн представить ее в виде клубка, намотанного из бесконечно длинной нити и лишенного какой-либо структуры.

Но примитивная компьютерная графика, отображающая уравнения Лоренца, показала, что эта траектория подчинена строгой логике и замкнута лишь в крошечной части доступного ей пространства. Создается впечатление, что она натянута на некую поверхность – микроскопически тонкую мембрану, форма которой, по иронии судьбы, похожа на пару крыльев бабочки. Траектория «наматывается» вокруг одного из таких крыльев, удаляясь по спирали от центра. Затем, приблизившись к краю крыла, она устремляется к другому крылу и начинает вращение по спирали вокруг этого крыла. Переходя то к одному крылу, то к другому, траектория совершает вокруг каждого крыла непредсказуемое количество витков. Это очень похоже на то, как водяное колесо совершает непредсказуемое количество поворотов то в одном, то в другом направлении.

Пытаясь разобраться в картине, которую предоставил ему компьютер, Лоренц понял, что здесь что-то «не так». Он знал, что траектория не может быть привязана к какой-то определенной поверхности: в противном случае она обязательно должна была пересекать сама себя. Крылья бабочки могли бы быть похожи на единую поверхность, но они должны были бы состоять из бесконечно большого количества слоев, упакованных настолько тесно между собой, что их невозможно было бы отличить друг от друга, подобно пластинкам слюды.

Такое сочетание бесконечно большого множества поверхностей – этот странный аттрактор – воплощает в себе новый вид порядка. Несмотря на то что «маршрут» траектории непредсказуем в деталях, он всегда остается на аттракторе, всегда пролегает через одно и то же подмножество состояний. Такая узость репертуара представляет собой проявление порядка, заложенного в хаосе, и объясняет, почему его сущность всегда остается неизменной.

Чтобы сделать эти абстракции более конкретными, попытайтесь представить себе странный аттрактор в виде футуристического автомобильного паркинга из фильма «Сумеречная зона» (Twilight Zone). Гараж полностью автоматизирован. Пока вы пассивно сидите за рулем автомобиля, буксирное устройство цепляет ваш автомобиль и перетаскивает его на свободное место в гараже. Подобно аттрактору Лоренца, гараж имеет два крыла; в данном случае будем называть их восточной и западной башнями, каждая из которых содержит бесконечно большое число уровней. Когда вы готовы отправиться в дорогу, вы нажимаете на кнопку, чтобы включить буксирное устройство. В течение какого-то времени вы спускаетесь и чувствуете, что спуск действительно происходит, хотя вас несколько мутит от бесконечного кружения по всем этим многочисленным уровням; внезапно у вас возникает ощущение, что вы отнюдь не приблизились к поверхности земли, оказавшись вместо этого у верхнего уровня противоположной башни. В ходе этой дьявольской езды вы продолжаете бесконечно кружить по многочисленным уровням, оказываясь в непредсказуемые моменты времени то в одной, то в другой башне. Вы обречены кружить по этим уровням до бесконечности. Хотя вам никак не удается выбраться из этой ловушки, ваш путь ни разу не повторяется. Вы можете случайно вернуться на тот же уровень той же башни, но никогда в ту же самую точку.

Такая вот судьба у траектории на аттракторе Лоренца. Буксирное устройство – это дифференциальное уравнение; именно оно определяет траекторию: и ее скорость, и ее направление в каждый момент времени. Эти правила носят совершенно детерминированный характер: судьба траектории определяется ее начальными условиями. Вернемся к нашей аналогии с паркингом: если каждый раз начинать с одного того же парковочного места в гараже, то вас вместе с вашим автомобилем будут буксировать каждый раз по одному и тому же пути, ускоряясь и замедляясь в одних и тех же местах. Эффект бабочки выражается посредством высокой зависимости от начальных условий: возвращаясь к аналогии с паркингом, если вас и человека, находящегося в соседнем с вами автомобиле, попросят покинуть стоянку в один и тот же момент времени, то в течение какого-то времени буксирное устройство будет перемещать вас обоих по одному и тому же маршруту – в чем вы оба можете легко убедиться, наблюдая друг за другом из окна своего автомобиля, – но очень скоро ваши пути и судьбы разойдутся. После этого картины вашего кружения в двух башнях окажутся совершенно некоррелированными. Тем не менее существование странного аттрактора обеспечивает некую разновидность порядка. Вы обречены на бесконечное кружение в этом гараже, повторяя до бесконечности одни и те же состояния, хотя и не в одной и той же последовательности.

Несмотря на то что описанная выше форма хаоса многим читателям покажется кошмарной, его голос звучит на удивление успокаивающе. Если его воспроизвести с помощью громкоговорителя, то окажется, что хаос звучит подобно так называемому белому шуму, подобно мягкой статике, которая помогает уснуть людям, страдающим бессонницей. Осенью 1988 г., когда у физика Лу Пекора родилась мечта[193] об использовании хаоса для каких-либо практических целей, он уловил в звуках, издаваемых хаосом, – в звуках, которые воспринимались всеми остальными исследователями лишь как примитивное, бессмысленное шипение, – надежду на осуществление своей мечты.

По жизни Лу Пекора – беззаботный и веселый человек со скромными манерами. В середине 1980-х годов он работал в научно-исследовательской лаборатории ВМС США, что в Вашингтоне, занимаясь изучением аннигиляции позитронов в твердых телах, спиновых волн в магнитах и некоторых других проблем физики твердого тела. Подумывая о том, чтобы сменить направление своих исследований, и будучи заинтригован ажиотажем вокруг теории хаоса (в то время это было самой животрепещущей темой в физике), он пытался найти оправдание переключения своих научных интересов на столь эзотерический предмет. Он знал, что его начальство отнесется к такому поступку более благосклонно, если он сможет указать какие-либо практические применения хаоса (например, в военной или какой-либо другой области). Столь прагматический подход к теории хаоса (который задним числом представляется вполне естественным) оказался полной неожиданностью для тех, кто занимался исследованием хаоса. До того времени этим занимались чистые теоретики, которых интересовала природа хаоса как таковая и которым не было никакого дела до того, найдутся ли какие-либо практические применения разрабатываемой ими теории.

Когда Пекора спросил у себя, можно ли поставить хаос на службу человеку, первое, о чем он вспомнил, была техника связи. Он подумал, нельзя ли упрятать в хаос секретные сообщения, осложнив таким образом противнику задачу передачи и расшифровки этих сообщений. Тот, кто пытается перехватить секретное сообщение, может даже не подозревать о том, что сообщение передано, или может испытывать немалые проблемы с выделением сообщения из шума. Пекора понимал, что сначала нужно уяснить, как синхронизировать хаотический передатчик с приемником, прежде чем можно было надеяться, что такая система шифрования сработает. Все формы беспроводной связи основаны на синхронизации. Например, в случае радио процесс настройки на определенную радиостанцию сводится к синхронизации приемника с частотой передачи соответствующего радиосигнала. После того как синхронизация будет достигнута, из принимаемого радиосигнала нужно выделить звук (для этого используется процесс так называемой демодуляции, то есть отделения звука от несущей частоты радиосигнала). В данном случае проблема заключалась в том, чтобы обобщить эту идею на хаос, когда в роли носителя выступает не периодическая, а хаотическая волна.

Пекора и Том Кэррол (в то время научный сотрудник с ученой степенью) не были специалистами в области связи. Впрочем, в теории хаоса они тоже были новичками, поэтому долго не могли решить, с чего им начать. В конце концов они решили, что получить какое-то представление об изучаемой ими проблеме лучше всего с помощью компьютерного моделирования. По крайней мере, в случае неудачи им не придется сожалеть о времени, затраченном на изготовление устройств, которые в конечном счете окажутся неработоспособными. Они немало повозились с компьютером, моделируя работу разных пар хаотических систем, связывая их между собой разными способами в надежде, что хаотические флуктуации этих систем каким-либо образом будут синхронизированы. Однако все их попытки не приводили к положительному результату. Эффект бабочки оказался слишком сильным. В течение какого-то непродолжительного времени моделируемая пара «передатчик-приемник» работала синхронно, после чего система неизменно рассинхронизировалась.

Немало разочаровавшись таким результатом, Пекора отправился в Хьюстон, на ежегодную конференцию по теории хаоса под названием Dynamics Days. Он сидел в зале, слушая лекции корифеев теории хаоса и безуспешно пытась сосредоточиться: его постоянно отвлекали мысли о нерешенной проблеме синхронизации. К концу конференции у него так и не появилось каких-либо конкретных идей относительно решения этой проблемы. Пекора улетел домой, едва успев на последний в тот день рейс. Он вернулся к себе домой уже после полуночи, чувствуя смертельную усталость и опустошенность. Жена и дети уже спали. Вскоре после того как он задремал, его разбудил плач семимесячной дочери Анны, которая, по-видимому, проголодалась. Жена сказала, что сама покормит дочь, но Пекора сказал, что будет лучше, если этим займется он.

Сидя в ночной тишине возле кроватки своей дочери и укачивая маленькую Анну у себя на руках, Пекора чувствовал, как постепенно уходит напряжение, накопившееся в нем за последнее время. Куда-то исчезли мысли, не дававшие ему покоя. Когда он вернулся к себе в постель, в его голове внезапно созрело решение. «Хаосом нужно управлять с помощью хаоса: я должен управлять приемником с помощью сигнала, который поступает с точно такой же системы». Хотя он тревожился, что за время сна может забыть эту интересную идею, он слишком устал, чтобы еще раз подняться с постели и зафиксировать ее на бумаге.

Проснувшись на следующее утро, Пекора вспомнил идею, которая пришла ему в голову ночью. Ему не терпелось проверить ее на практике. Он хотел проверить ее на уравнениях Лоренца, но еще не освоил как следует решение дифференциальных уравнений на компьютере, поэтому решил взять за основу какую-либо хаотическую систему, которую было бы легче запрограммировать. Пекора начал свой эксперимент со случая, когда передатчик и приемник пребывают в разных состояниях, и попросил компьютер предсказать их поведение по истечении продолжительного времени. Когда компьютер начал выдавать результаты моделирования, стало очевидно, что данные указывают на апериодичность, вполне естественную для хаоса, но – и это было удивительно! – значения сближались между собой. Это означало, что передатчик и приемник синхронизировались! Управляя приемником с помощью хаотического сигнала, передаваемого с его дубликата, вы можете заставить эту пару работать синхронно.

С технической точки зрения схему Пекора[194] можно описать следующим образом. Берем два экземпляра одной и той же хаотической системы. Один из этих экземпляров рассматриваем как задатчик; применительно к системам связи он будет выполнять функции передатчика. Другой экземпляр принимает сигналы от задатчика, но не отправляет никаких сигналов. Связь имеет одностороний характер. (Подходящей аналогией может служить военный командный центр, отправляющий зашифрованные приказы военнослужащим в поле или на корабле.) Чтобы синхронизировать эти две системы, отправляем в приемник постоянно меняющееся численное значение одной из переменных задатчика и используем его для замены соответствующей переменной приемника – и так в каждый очередной момент времени. Пекора обнаружил, что при определенных условиях все другие переменные приемника – те, которые не были заменены – автоматически входят в синхронизм со своими аналогами в задатчике. В результате будут совпадать все переменные. Две системы окажутся полностью синхронизированны.

Это описание, пусть и правильное с математической точки зрения, не передает удивительный феномен синхронизированного хаоса. Чтобы оценить всю необычность этого явления, представьте переменные хаотической системы в виде современных танцоров. По аналогии с уравнениями Лоренца, назовем их x, y и z. Каждый вечер они выступают на сцене, устраивая между собой своеобразную «отработку» сигналов, поступающих от партнеров: каждый танцор отвечает даже на едва заметные сигналы двух других танцоров. Несмотря на то что их повороты и жесты кажутся тщательно отрепетированными, это вовсе не так. С другой стороны, они вовсе не импровизируют – по крайней мере не импровизируют в обычном смысле этого слова. В том, как они танцуют, нет ничего случайного, никакого намека на импровизацию. В зависимости от того, в каком именно месте сцены в данный момент находятся два других танцора, третий реагирует в соответствии с определенными правилами. Хитрость заключается в изощренности самих правил. Они гарантируют, что результирующее выступление всегда будет элегантным и никогда – монотонным; оно всегда наполнено пассажами, которые напоминают друг друга, но никогда не повторяют друг друга. Каждую минуту в танце появляется что-то новое (такова уж природа апериодичности), каждый вечер выступление танцоров не похоже на их предыдущее выступление (сказывается эффект бабочки); тем не менее, по своей сущности, выступление всегда остается одним и тем же, поскольку оно всегда следует одному и тому же странному аттрактору.

До сих пор мы рассматривали метафору для одной системы Лоренца, играющей роль приемника в схеме связи, предложенной Пекорой. Теперь допустим, что время остановилось на мгновение. Приостановилось действие законов Вселенной. В этот ужасный момент x бесследно исчезает. На его месте появляется новая переменная; назовем ее x?. Эта новая переменная похожа на x, но она запрограммирована таким образом, чтобы не обращать внимания на локальные y и z. Поведение x? определяется дистанционно ее взаимодействием с y? и z?, переменными в передатчике, находящемся где-то далеко, в другой системе Лоренца, причем все они являются частью некого невидимого задатчика.

Все это очень похоже на классический фильм ужасов «Вторжение похитителей тел» (Invasion of the Body Snatchen). С точки зрения принимающей системы, эта новая переменная x должна казаться необъяснимой. «Мы пытаемся танцевать с x, но он почему-то перестал реагировать на все наши сигналы», – думают y и z. «Никогда раньше мне не приходилось видеть подобного поведения x», – говорит один из них. «Эй, x, – шепчет другой, – это действительно ты?» Но на лице x сохраняется непроницаемое выражение. Точно так же, как в упомянутом мною фильме, x является порождением стручка, то есть стручком, принявшим вид x. Он уже не танцует вместе с y и z – теперь его партнерами являются y? и z?, невидимые призрачные двойники y и z, удаленные переменные в параллельном мире задатчика. В этой удаленной системе поведение x? представляется совершенно нормальным. Но в результате телепортации на приемник x? выглядит на удивление неотзывчивым. Это объясняется тем, что x приемника был похищен, подменен этим странным x?, возникшим словно ниоткуда. Будучи весьма чувствительными созданиями, y и z вносят соответствующие поправки в свой танец. Вскоре нормальное взаимодействие всей троицы x, y и z восстанавливается: они выделывают свои «па» совершенно непринужденно, плавно перемещаясь по пространству состояний на аттракторе Лоренца и создавая перед нашим взором картину неповторимой «хаотической грации».

Однако самым зловещим и сверхъестественным в этой картине оказывается то, что сами y и z к этому времени уже превратились в порождения стручков. Сами о том не подозревая, они сейчас идеально синхронно танцуют со своими собственными призрачными двойниками y? и z?, переменными, с которыми они еще никогда не встречались. Каким-то образом, исключительно благодаря влиянию телепортированного x?, была также передана информация об удаленных y? и z?, причем этой информации оказалось достаточно, чтобы синхронизировать приемник с задатчиком. Теперь оказались «рекрутированными» все три переменные x, y и z. Невидимый задатчик, в полном соответствии со своим названием, «задает тон».

Компьютерное моделирование, выполненное Пекорой, показало, что его схема оказалась работоспособной применительно к уравнениям в компьютере. Теперь вопрос заключался в том, окажется ли его схема работоспособной в лабораторных условиях, то есть в условиях, когда никакие две системы не могут быть совершенно идентичны друг другу и не могут быть полностью ограждены от сторонних возмущений. Пекора рассмотрел вопрос о том, какие хаотические системы оказались бы наиболее управляемыми с экспериментальной точки зрения. Выбор сразу же пал на электронные цепи по причине их высокого быстродействия, дешевизны и удобства выполнения измерений, что позволяло получить значительный объем данных за короткое время. Кэррол согласился с этими доводами и принялся за работу, пытаясь воплотить уравнения Лоренца в электронных устройствах. Почти сразу же он зашел в тупик. Реализация этих уравнений предполагала выполнение операций умножения переменных x, y и z. Для выполнения этих операций электронным способом требовались микрочипы множителей, но Кэррол пришел к выводу, что готовые компоненты, имевшиеся в его распоряжении, не могли обеспечить требуемую точность вычислений. Более серьезная проблема заключалась в том, что в ходе функционирования системы значения переменных в уравнениях Лоренца изменялись в 100 тысяч раз. Столь широкий динамический диапазон превышал возможности типичных устройств питания электронных устройств. Таким образом, Пекора и Кэррол были вынуждены отказаться от идеи создания электронной цепи Лоренца.

Пытаясь найти более подходящую альтернативу, Пекора и Кэррол обратились за помощью к Роберту Ньюкомбу, электроинженеру из Мэрилендского университета, который к тому времени уже разработал свой собственный вариант хаотических цепей. Ньюкомб дал полную волю своему творческому воображению. Он не видел категорической необходимости в том, чтобы разрабатывать цепи, которые моделировали бы лоренцовы водяные колеса, или лазеры, или какую-либо другую физическую систему – его просто интересовал хаос как таковой, и он хотел исследовать хаос электронным способом. Кэррол воспользовался одним из рецептов Ньюкомба и подтвердил, что полученная таким образом электронная цепь генерировала хаотические флуктуации напряжения и тока. Отображаемые на экране осциллографа, эти переменные вырисовывали странный аттрактор – не точно такой же, как крылья бабочки Лоренца, но похожий на него. Скорость работы этой цепи составляла тысячи циклов в секунду; она создавала быстрый и прекрасный хаос.

Теперь можно было приступить к тестированию схемы синхронизации. Кэррол изготовил второй экземпляр своей цепи и подсоединил его к первому экземпляру согласно правилам Пекоры. В соответствии с теорией эти две цепи должны были осциллировать нерегулярно, хаотически, но в идеальном синхронизме между собой. Чтобы протестировать их синхронизм, Кэррол настроил осциллограф на отображение графика зависимости напряжения на приемнике y от его аналога на передатчике – y?. В случае равенства этих двух переменных они должны попадать на диагональ, проходящую под углом 45 градусов (поскольку, если значения y отображаются по горизонтали, а значения y? – по вертикали, то горизонтальное смещение y должно равняться вертикальному смещению y? в случае, если их значения всегда равны между собой). А поскольку значения y и y? все время меняются, от момента к моменту, они должны бегать вдоль диагонали туда и обратно, никогда не отклоняясь от нее.

Кэррол нажал на кнопку, чтобы запустить свою систему. Понадобилось всего две миллисекунды, чтобы оба напряжения оказались на диагонали, после чего они оставались на ней до завершения эксперимента. «У меня становятся дыбом волосы на голове, когда я думаю об этом, – рассказывал мне Пекора. – Вряд ли я еще когда-нибудь в своей жизни переживу подобный момент. Это все равно как присутствовать при рождении своего ребенка».

Декабрь 1991 г. Последний день занятий в МТИ. Только что я закончил чтение последней лекции своего курса по теории хаоса. Все слушатели, за исключением одного аспиранта, покинули аудиторию. Сияя от гордости, он протянул мне лист бумаги, испещренный формулами и теоремами, каждая из которых была обведена аккуратной прямоугольной рамкой. При подготовке к предстоящему выпускному экзамену он умудрился представить весь курс по теории хаоса на единственном листе бумаги. Оценив его каллиграфический почерк, я понял, что имею дело с неординарной личностью. Так оно и было на самом деле: Кевин Куомо оказался одним из лучших аспирантов курса.

Куомо в это время только писал диссертацию. Ее темой было исследование синхронизированного хаоса в электрических цепях и возможность их использования в системах связи. В то время я имел некоторое представление о статье Кэррола и Пекоры, опубликованной в 1990 г., но еще не успел ознакомиться с ней основательно. Куомо хотел поделиться со мной всем, что он думает по поводу этой статьи, и буквально взахлеб рассказывал мне о ней, но затем переключился на собственную работу и предложил мне ознакомиться с цепью, которую он сам сконструировал. Это было первое в мире электронное воплощение уравнений Лоренца. Он также просил меня проверить выполненное им математическое доказательство – демонстрацию новой схемы синхронизации, удовлетворяющей уравнениям Лоренца вне зависимости от способа запуска приемника и передатчика. Куомо на мгновение остановился, а затем продолжил: Пекора и Кэррол не предложили никакого подобного доказательства, и это обстоятельство беспокоит его. Логика предложенного им доказательства не была слишком сложной – лишь стандартное применение функций Ляпунова, подобное тому, которое встречалось у нас на занятиях. Эта простота настораживала его: может быть, он в чем-то ошибается, что-то упустил из виду?

Оказалось, что Куомо ни в чем не ошибся. Предложенное им доказательство было безупречным, а разработанная им цепь действительно моделировала уравнения Лоренца (впоследствии Пекора честно признался в том, что до сих пор не представляет, как Куомо удалось додуматься до такого решения). Однако сейчас Куомо знаменит вовсе не этим. Впоследствии ему и его консультанту Элу Оппенгейму удалось упервые в мире продемонстрировать практическую возможность хаотического шифрования информации: синхронизированный хаос действительно можно использовать для повышения безопасности информации, передаваемой по каналам связи.

Их метод основан на маскировании, то есть применяется та же стратегия, которая используется (безуспешно и незабываемо) скрытной парочкой из фильма Френсиса Форд Копполы «Разговор» (The Conversation). Чувствуя, что за ними ведется слежка, мужчина и женщина бродят по многолюдной городской площади и разговаривают друг с другом шепотом, надеясь, что громкие звуки, издаваемые уличными музыкантами, помешают окружающим подслушать их разговор. В версии Куомо и Оппенгейма фоновый шум создается шипением электрического хаоса, генерируемого переменной x в цепи Лоренца. Прежде чем какое-либо сообщение будет отправлено на приемник, на него налагается x, чтобы замаскировать это сообщение. Для большей надежности x должен быть намного громче самого сообщения (точно так же, как уличная музыка должна быть намного громче разговора шепотом) во всем его диапазоне частот. Разумеется, если приемник не может отделить сообщение от маски, такая система оказывается неработоспособной. Для решения этой проблемы применяется синхронизация. Схема Куомо гарантирует, что приемник, когда на него поступает гибридный сигнал (сообщение плюс маска), синхронизируется с маской, а не с сообщением. В результате приемник регенерирует чистую версию маски. Извлекая ее из гибридного сигнала путем вычитания, мы получаем интересующее нас сообщение. Этот метод обеспечивает безопасность передаваемой информации, поскольку тому, кто попытается перехватить сообщение, будет весьма проблематично выполнить такую же декомпозицию: он не будет знать, что именно нужно вычесть, какая часть комбинированного сигнала является маской, а какая часть – сообщением.

Через год после того как Куомо прослушал мой курс, он вернулся, чтобы «вживую» продемонстрировать свою схему шифрования нынешним студентам. Сначала он показал нам схему своего передатчика – небольшую печатную плату с напаянными на нее резисторами, конденсаторами, операционными усилителями и микросхемами аналогового умножителя. Напряжения x, y и z в трех разных точках этой схемы были пропорциональны одноименным переменным Лоренца. Когда на экране осциллографа отобразился график зависимости x от y, мы увидели хорошо знакомые нам очертания крыльев бабочки странного аттрактора. Затем, подключив к передатчику громкоговоритель, Куомо предоставил нам возможность услышать звуки хаоса. Он потрескивал, подобно разрядам статического электричества, – вполне привычный для нас фон, который мы слышим во время радиопередачи. Затем Куомо взял еще одну печатную плату – приемник, являющийся двойником передатчика, и соединил их между собой с помощью зажима типа «крокодил» в месте, специально предназначенном для этой цели. Еще раз воспользовавшись осциллографом, он продемонстрировал нам, что обе схемы, передатчик и приемник, теперь работают синхронно, о чем свидетельствовала упоминавшаяся выше диагональ, пересекающая экран осциллографа под углом 45 градусов.

Куомо произвел в аудитории настоящий фурор, когда использовал эти схемы, чтобы замаскировать сообщение, в качестве которого он выбрал необычайно популярную в то время песню «Эмоции» в исполнении Мэрайи Кэри. (Один из присутствовавших в аудитории, которому, очевидно, не очень-то нравилась эта песня, поинтересовался: «Это полезный сигнал или шум?») После воспроизведения первоначальной версии песни Куомо проиграл замаскированную версию. Слушая это шипение, было совершенно невозможно догадаться, какая песня скрывается за ним. Однако когда замаскированное сообщение было передано на приемник, сигнал на выходе оказался практически идеально синхронизирован с исходным хаосом, а после мгновенного электронного вычитания мы снова услышали пение Мэрайи Кэри. Звучание было далеким от идеального, но вполне разборчивым.

Когда статья Куомо и Оппенгейма[195] была опубликована в 1993 г., объявленные в ней результаты ничуть не удивили Лу Пекору. К тому времени он вместе с Томом Кэрролом уже три года действовал примерно в том же направлении, но у них не было возможности опубликовать свои результаты.

Еще осенью 1989 г., после того как их хаотические цепи были успешно синхронизированы, Пекора и Кэррол приступили к решению проблемы хаотического шифрования. Обладая чрезвычайно ограниченными познаниями в области теории связи и кодирования, они выбрали весьма неуклюжий метод, предполагавший отправку двух сигналов. Один сигнал использовался для установления синхронизма между приемником и передатчиком. Второй сигнал представлял собой гибрид: маску с сообщением, добавленным к ней при очень низком уровне мощности. По сути, это та же стратегия, которую через пару лет предложили Куомо и Оппенгейм, хотя и менее элегантная в том смысле, что метод Куомо использует лишь один сигнал (x плюс сообщение), выполняющий двойную работу: он не только устанавливает синхронизм, но и переносит сообщение. Но в целом идея одна и та же.

Группа «Звездные войны» (Space Warfare) в научно-исследовательской лаборатории ВМС США заинтересовалась работой Пекоры и Кэррола, поскольку она открывала возможность использования новых способов кодирования и шифрования спутниковой связи. Они финансировали работу Кэррола в предыдущем году и теперь хотели присмотреться повнимательнее к тому, чем занимаются эти два физика. Руководитель группы предложил Пекоре помалкивать о своей работе до тех пор, пока люди из «Звездных войн» не оценят ее эффективность: они намеревались привлечь к оценке этой работы стороннего эксперта. Пекоре были даны четкие инструкции относительно того, как вести себя. Ему и Кэрролу не разрешалось задавать эксперту какие-либо вопросы: ни в какой организации он работает, ни даже выяснять его фамилию. «Как же нам обращаться к нему?» – спросил Пекора. «Зовите его Билл», – посоветовал руководитель группы. Между собой Пекора и Кэррол звали его д-р Х.

Д-р Х оказался молодым человеком, серьезным и весьма компетентным специалистом в своей области. Он таскал за собой компьютер, напичканный программами моделирования аналоговых цепей. Похоже, он не очень-то разбирался в теории хаоса, но был хорошо знаком с теорией связи. Ему удалось довольно быстро выполнить компьютерное моделирование цепей, предложенных Пекорой и Кэрролом. Впоследствии их проинформировали о том, что д-р Х пришел к выводу, что их цепи функционируют в полном соответствии с описанием, хотя он и сомневался в том, можно ли привести эти цепи к цифровому виду, обеспечивающему достаточную степень их защищенности.

Вскоре к оцениванию схем Пекоры и Кэррола подключились другие члены группы «Звездные войны». Пекора по наивности поспорил с одним из них на бутылку пива, что сможет упрятать в хаос синусоидальный сигнал, и предложил своему визави извлечь этот сигнал. Тот запустил систему в работу на минуту, измерил кривые напряжения, затем выполнил вычисление, называемое быстрым преобразованием Фурье, чтобы измерить силу каждой из составляющих частот, переданных в ходе этого быстротечного эксперимента. Синусоидальная кривая предстала на экране в виде выступа на спектре. Пекора понял, что с теорией шифрования ему следует ознакомиться более основательно.

Члены группы «Звездные войны» пришли к выводу, что эта новая схема представляет определенный интерес, однако это вовсе не то, на что могли бы рассчитывать ВМС. В конце концов Пекоре и Кэрролу разрешили опубликовать полученные ими результаты, но поскольку они хотели оформить патент на изобретение, их юрист посоветовал еще немного помолчать о выполненной ими работе. Таким образом, они приняли решение повременить с публикацией.

Кроме того, группа «Звездные войны» свела Пекору и Кэррола с одним из сотрудников Агентства национальной безопасности (АНБ), сверхсекретной государственной организации, занимающейся, в частности, вопросами кодирования и декодирования информации. Пекора посетил штаб-квартиру АНБ и ознакомил с полученными им результатами группу шифровальщиков, которые внимательно выслушали его доклад, но не ответили ни на один из его вопросов. «Мне казалось, что я общаюсь с черной дырой, – рассказывал впоследствии Пекора. – Информация входит в эту дыру, но ничего не выходит из нее». После визита в АНБ Пекора понял, что забыл сообщить им кое-что еще. Одним словом, ему понадобилось еще раз связаться с сотрудником, который организовал ему посещение штаб-квартиры АНБ. Поскольку Пекора потерял номер телефона этого сотрудника АНБ, он заглянул в телефонный справочник и, к немалому своему удивлению, обнаружил там номер этой сверхсекретной организации. Он набрал этот номер и вышел таким образом на сотрудника справочной службы АНБ. Их общение напоминает один из скетчей известной комик-группы «Монти Пайтон»:

Проделанная ранее работа над синхронизированным хаосом вселила немалый оптимизм относительно перспектив хаотического шифрования, особенно в физиков, имеющих лишь весьма приблизительное представление о криптографии. В начале 1990-х годов в физических журналах можно было встретить немало статей, заголовки которых будили в читателях надежду на скорое наступление эры «безопасной» связи. Впрочем, специалистам было виднее, как в действительности обстоит дело. С самого начала Эл Оппенгейм предостерегал Куомо и меня от чрезмерной эйфории по поводу достигнутых результатов. «Этот метод ни в коем случае нельзя назвать безопасным, – предупреждал нас Оппенгейм. – Безопасный – значит такой, который невозможно взломать. Нам не известно наверняка, безопасен ли этот метод. Возможно, он обеспечивает какой-то – достаточно невысокий – уровень безопасности, но это, пожалуй, и все, на что он способен. Схемы маскирования взломать не так уж сложно».

Для тех, кто пользуется мобильными телефонами, даже минимальный уровень безопасности является большим благом[196]. Такой уровень безопасности оказался бы вполне достаточным для принцессы Дианы, когда журналисты перехватили разговор с ее любовником Джеймсом Гилби, впоследствии опубликованный под названием Squidgy («Мягкий»). В 1989 г. журналисты перехватили еще более интимный телефонный разговор принца Чарльза с Камиллой Паркер Боулз. Когда Ньют Гингрич обсуждал вместе со своими юристами выдвинутое против него обвинение в нарушении этических норм, их переговоры по мобильной связи были перехвачены и записаны сторонниками Демократической партии с помощью полицейского сканера. Устройства шифрования разговоров по мобильной связи существуют и в наши дни, однако их стоимость составляет несколько сотен долларов. Хаотическое маскирование могло бы оказаться более дешевой альтернативой для борьбы с потенциальными любителями перехватывать информацию, передаваемую по мобильной связи.

Что же касается применения в военной и финансовой сферах, то для этого требуется гораздо более безопасное шифрование. На данный момент методы шифрования, основанные на теории хаоса, оказались обескураживающе слабыми. Кевин Шорт[197], математик из университета штата Нью-Гэмпшир, продемонстрировал, насколько легко взломать практически любой хаотический код из тех, которые предложены на сегодняшний день. Когда он размаскировал лоренцов хаос Куомо и Оппенгейма, полученные им результаты инициировали своего рода «гонку вооружений» между специалистами, занимавшимися проблемами нелинейности, которые пытались разработать еще более сложные системы шифрования информации. Однако в конечном счете победа осталась за взломщиками кодов.

Одной из самых многообещающих разработок стал проект 1998 г. Его авторами были Грегори Ванвиггерен и Раджаршри Рой, физики из Технологического института штата Джорджия. Они провели первую экспериментальную демонстрацию хаотической связи[198], реализованной с помощью лазеров и волоконно-оптической линии связи, вместо обычных электронных генераторов сигналов и проводных линий связи. В оптической системе связи Ванвиггерена и Роя хаотические волны света служили носителями скрытых в них сообщений, передавая информацию от одного лазера к другому со скоростью 150 миллионов бит в секунду, то есть в тысячи раз быстрее, чем передают информацию обычные электронные устройства. При этом не существует каких-либо препятствий, по крайней мере на теоретическом уровне, для достижения еще больших скоростей.

Еще одно преимущество передачи информации с помощью хаотических лазеров заключается в том, что генерируемый ими хаос оказывается гораздо более сложным, что существенно усложняет взлом кодов. Степень сложности определяется числом, которое получило название «размерности странного аттрактора»[199] и представляет собой естественное обобщение обычной концепции размерности пространства. Однако в отличие от прямой линии (одномерный случай) или плоскости (двумерный случай), размерность странного аттрактора обычно представляет собой дробное число. Например, лоренцов аттрактор состоит из бесконечно большого числа двумерных (плоских) листов, из чего следует, что он обладает бесконечно большой поверхностью, но не имеет объема. Как бы загадочно это ни звучало, он представляет собой нечто большее, чем поверхность, но вместе с тем нечто меньшее, чем объемное тело, а его размерность, соответственно, больше 2, но меньше 3. Для волоконно-оптических систем передачи информации Ванвиггерена и Роя, построенных на основе лазеров, легированных эрбием, размерность странного аттрактора неизвестна, но почти наверняка она представляет собой дробное число и, что еще важнее, она огромна. Вполне вероятно, что она является числом, не меньшим 50, то есть соответствует чрезвычайно сложной форме хаоса. Остается лишь убедиться в том, что эта новая форма кодирования окажется более безопасной, чем ее предшественники.

Если же оставить в стороне шифрование, то наиболее важное значение синхронизированного хаоса для нас может заключаться в том, как он углубил наше понимание синхронизма как такового. Теперь синхронизм уже не будет ассоциироваться у нас лишь с ритмичностью, цикличностью и повторяемостью. Синхронизированный хаос поставил нас лицом к лицу с совершенно новым видом порядка во Вселенной или, по крайней мере, с порядком, который не встречался нам ранее: некой формой преходящего артистизма, который, как нам когда-то казалось, присущ лишь человеку. Это свидетельствует о том, что синхронизм представляет собой еще более распространенное и еще более утонченное явление, чем нам когда-то казалось.