Книга: Математика космоса [Как современная наука расшифровывает Вселенную]

* * *

Несмотря на то что в общем случае задача трех тел — описать, как движутся три точечные массы под действием гравитации Ньютона, — чрезвычайно тяжело решается математически, кое-какие полезные результаты можно получить, сосредоточившись на особых случаях. Важнейший среди них — это задача «двух с половиной тел», математическая шутка с серьезным смыслом. В этой задаче два тела обладают ненулевыми массами, а третье настолько мало, что его массой можно попросту пренебречь. Примером такой задачи может служить пылинка в поле тяготения Земли и Луны. Основная идея модели заключается в том, что пылинка реагирует на гравитационное воздействие Земли и Луны, но сама она настолько легка, что, по существу, никак не влияет ни на одно, ни на второе тело. Закон всемирного тяготения Ньютона говорит нам, что пылинка все же оказывает влияние, хоть и очень слабое, но влияние это так мало, что при моделировании его можно просто проигнорировать. На практике такой подход работает и с более крупным телом, таким как космический аппарат, небольшая луна или астероид, если промежуток времени, о котором идет речь, достаточно мал, чтобы исключить существенные хаотические эффекты.

В этой модели возможно еще одно упрощение: можно считать, что два крупных тела движутся по круговым орбитам. Это позволяет нам перевести всю задачу во вращающуюся систему отсчета, по отношению к которой большие тела неподвижны и лежат на фиксированной плоскости. Представьте себе большую поворотную площадку. Теперь закрепим Землю и Луну на площадке таким образом, чтобы соединяющая их прямая проходила через центральный шарнир, а сами они располагались от него по разные стороны. Масса Земли примерно в 80 раз превышает массу Луны; если мы поместим Луну в 80 раз дальше от шарнира, чем Землю, то общий центр масс этих двух тел как раз совпадет с шарниром. Далее, если вращать площадку вместе с закрепленными на ней Землей и Луной с правильной скоростью, то планеты будут двигаться по круговым орбитам в полном соответствии с законом всемирного тяготения. При этом в системе координат, связанной с поворотной площадкой, оба тела останутся неподвижны, но будут испытывать на себе эффект вращения в виде «центробежной силы». Это не настоящая физическая сила: она возникает потому, что тела приклеены к площадке и не могут двигаться по прямой. Однако центробежная сила точно так же влияет на динамику тел во вращающейся системе координат, как это делала бы настоящая сила. Ее часто называют «фиктивной силой», несмотря на то, что действие она оказывает самое настоящее.

В 1765 году Эйлер доказал, что в такой модели можно добиться, чтобы все три тела двигались по круговым орбитам в соответствии с законом всемирного тяготения, приклеив пылинку на той же самой прямой, что и два других тела. В этой точке гравитационные силы со стороны Земли и Луны в точности компенсируются центробежной силой, которую испытывает пылинка. Мало того, Эйлер нашел три такие точки. Одна из них (в настоящее время мы называем ее L₁) лежит между Землей и Луной. L₂ располагается за Луной, если смотреть на нее с Земли; L₃ лежит по ту сторону Земли, если смотреть на нее с Луны.

В обозначениях этих точек используется буква L, а не E, как можно было ожидать, потому что в 1772 году Лагранж нашел еще две возможные локации для пылинок. Они лежат не на линии Земля — Луна, а в вершинах двух равносторонних треугольников, двумя другими углами которых являются Земля и Луна. В этих точках пылинка остается неподвижной относительно Земли и Луны. Точка Лагранжа L₄ располагается на 60° впереди Луны, а L₅ — на 60° позади. Лагранж доказал, что для любых двух тел существует ровно пять таких точек.

Радиусы орбит, соответствующих точкам L₄ и L₅, в общем случае отличаются от радиусов орбит двух других тел. Однако если одно из этих тел много массивнее другого (к примеру, если это Солнце, а другое тело — планета), то общий центр масс и более массивное тело почти совпадают. В этом случае орбиты, соответствующие L₄ и L₅, почти совпадают с орбитой менее массивного тела.

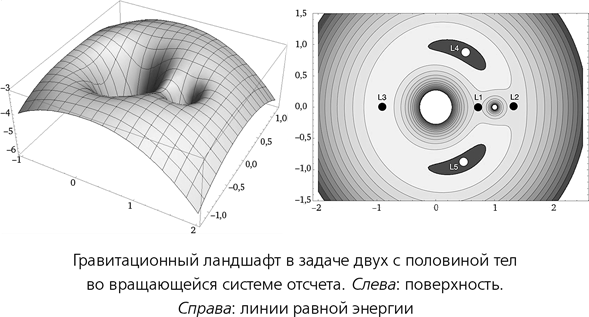
Геометрию точек Лагранжа можно вывести из выражений для энергии пылинки. Энергия эта состоит из кинетической (пылинка вращается вместе с поворотной площадкой) и потенциальной (связанной с гравитационным притяжением Земли и Луны) составляющих. На рисунке полная энергия пылинки показана двумя способами: в виде изогнутой поверхности, высота которой представляет полную энергию, и в виде системы горизонталей — кривых, во всех точках которых энергия постоянна. Поверхность можно рассматривать как некий гравитационный ландшафт. Пылинка может двигаться по этому ландшафту, но до тех пор, пока на нее не подействует какая-нибудь дополнительная сила, закон сохранения энергии требует, чтобы она оставалась на одной горизонтали. В общем, она может двигаться вбок по склону холма, но не вниз и не вверх.

Если «линия» горизонтали представляет собой одну-единственную точку, пылинка будет находиться в равновесии — она останется в той точке поворотной площадки, куда вы ее поместите. Существует пять таких точек, на рисунке с горизонталями они обозначены как L₁ — L₅. В точках L₁, L₂ и L₃ энергетическая поверхность имеет форму седла: в одних направлениях она уходит вниз, в других — вверх. Точки L₄ и L₅, напротив, располагаются на вершинах энергетического ландшафта. Важная разница между одними и другими точками состоит в том, что вершины (и локальные впадины, которых здесь нет) окружены небольшими замкнутыми горизонталями, очень близкими к собственно верхушке пика. В седловинах не так: горизонтали вблизи любой точки уходят прочь, и хотя, возможно, когда-нибудь где-нибудь замыкаются, но делают это не сразу и далеко не рядом.

Если пылинку чуть сдвинуть с точки Лагранжа, она окажется на одной из ближайших к ней горизонталей и будет по ней двигаться. В случае седловидной поверхности любая такая горизонталь уведет объект далеко от первоначальной позиции. К примеру, если пылинка, находясь в точке L₂, чуть сдвинется вправо, она попадет на громадную замкнутую горизонталь, которая уведет ее далеко-далеко, вокруг Земли, за точку L₃ на дальней стороне планеты. Поэтому можно сказать, что равновесие в точке на седловидной поверхности может быть только неустойчивым: первоначальное небольшое возмущение затем многократно увеличивается. На вершинах и во впадинах равновесие устойчиво: ближайшие к ним горизонтали замкнуты и целиком располагаются вблизи точки равновесия. Небольшое первоначальное возмущение небольшим и останется. Тем не менее сдвинутая пылинка уже не находится в равновесии: ее реальное движение складывается из небольших колебаний по замкнутому контуру и общего вращения поворотной площадки. Подобные орбиты называют орбитами-головастиками. Главное, что о них можно сказать, это то, что пылинка остается вблизи пика.

(Я здесь немного схитрил, поскольку на рисунке показаны положения объектов, но не их скорости. Отклонения по скорости усложняют реальную орбиту, но вывод об устойчивости равновесия остается верным. См. главу 9.)

Точки Лагранжа — это те особенности гравитационного ландшафта, которые можно с выгодой использовать при планировании космических полетов. В 1980-е годы наблюдался всплеск интереса к космическим колониям — гигантским искусственным обиталищам, где люди могли бы жить и, пользуясь солнечным светом как источником энергии, выращивать для себя пищу. В частности, они могли бы жить на внутренней стороне пустотелого цилиндра, если бы тот вращался вокруг своей оси, создавая тем самым искусственную гравитацию при помощи центробежной силы. Точка Лагранжа — привлекательное место для строительства такого космического дома, поскольку здесь любое тело пребывает в равновесии. Даже в седловине, в одной из точек неустойчивого равновесия — L₁, L₂ или L_3, — достаточно будет небольших импульсов от включаемых изредка ракетных двигателей, чтобы удержать сооружение на месте и не дать ему уйти. Пиковые точки — L₄ и L₅ — подходят еще лучше; там не нужна вообще никакая коррекция.