Книга: Математика космоса [Как современная наука расшифровывает Вселенную]

* * *

Поиск закономерностей в массиве данных чем-то сродни магическому искусству, но математические техники несколько облегчают задачу. Один из фундаментальных принципов такого поиска гласит, что разные способы численного или графического представления данных способны выявить разные их свойства.

Приведенная иллюстрация позволяет предположить, что в пределах основного пояса астероиды распределены достаточно однородно. Кольцо точек кажется примерно одинаково плотным везде, без пробелов или сгущений. Но опять же, и эта картина вводит зрителя в заблуждение. Ее масштаб не позволяет показать подробности; к тому же, и это даже важнее, на ней показаны текущие положения астероидов. Чтобы увидеть интересную структуру — помимо двух скоплений, подписанных как «троянцы» и «ахейцы», к которым мы еще вернемся, — необходимо взглянуть на расстояния. На самом деле главная характеристика здесь — период обращения[36], но он непосредственно связан с расстоянием через третий закон Кеплера.

В 1866 году астроном-любитель по имени Дэниел Кирквуд обратил внимание на прорехи в поясе астероидов. Точнее говоря, он заметил, что астероиды редко занимают орбиты, лежащие на определенных расстояниях от Солнца, если измерять их большой полуосью орбитального эллипса. На рисунке показан современный расширенный график числа астероидов в зависимости от расстояния в основной части пояса, на расстояниях от 2 до 3,5 а.е. от Солнца. Три резких провала, в которых число астероидов падает до нуля, очевидны. Еще один провал имеется возле 3,3 а.е., но он не настолько очевиден, потому что это уже окраина астероидного пояса и тел там значительно меньше. Эти провалы получили название люков или щелей Кирквуда.

Люки Кирквуда не видны на предыдущем рисунке по двум причинам. Во-первых, точки, изображающие астероиды, намного больше реального размера астероидов в масштабе рисунка, а во-вторых, «щели» наблюдаются на расстояниях, а не в конкретных местах. Каждый астероид движется по эллиптической орбите, и расстояние от него до Солнца постоянно меняется. Так что астероиды проходят через щели; они просто не остаются в них надолго. Большие оси орбитальных эллипсов ориентированы очень по-разному. Эти эффекты делают прорехи (щели) в поясе астероидов настолько размытыми, что увидеть их на рисунке невозможно. Однако постройте гистограмму для расстояний — и они тут же проявятся.

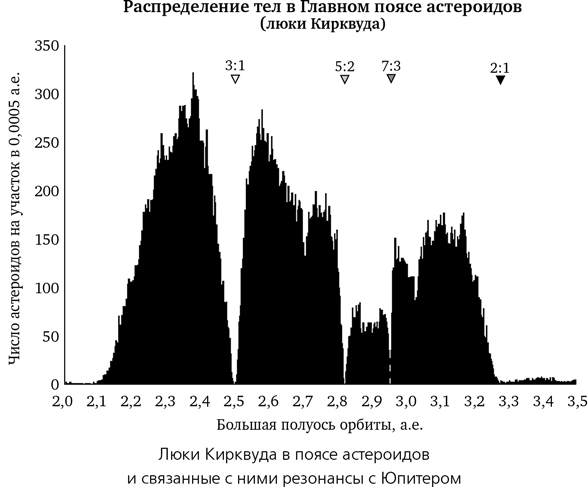
Кирквуд правильно предположил, что замеченные им щели созданы мощным гравитационным полем Юпитера. Оно оказывает влияние на каждый астероид пояса, но между резонансными и нерезонансными орбитами существует значительная разница. Очень глубокий провал слева на графике соответствует орбитальному расстоянию, на котором астероид находится с Юпитером в резонансе 3:1, то есть совершает три оборота вокруг Солнца на один оборот Юпитера. Периодическое повторение одних и тех же взаимных позиций усиливает долговременные эффекты тяготения Юпитера.

В данном случае резонансы расчищают соответствующие области пояса. Орбиты астероидов, находящихся в резонансе с Юпитером, становятся более вытянутыми и хаотичными до такой степени, что начинают пересекать орбиты внутренних планет, в первую очередь Марса. Происходящие иногда сближения с Марсом еще сильнее изменяют их орбиты, выбрасывая такие астероиды в случайных направлениях. По мере того как этот эффект заставляет уходить все больше астероидов из зоны возле резонансной орбиты, там и возникает люк.

Основные люки (в скобках указаны соответствующие резонансы) располагаются на расстояниях 2,06 а.е. (4:1); 2,50 а.е. (3:1); 2,82 а.е. (5:2); 2,95 а.е. (7:3) и 3,27 а.е. (2:1). Существуют более слабые, или узкие, щели на расстояниях 1,90 а.е. (9:2); 2,25 а.е. (7:2); 2,33 а.е. (10:3); 2,71 а.е. (8:3); 3,03 а.е. (9:4); 3,08 а.е. (11:5); 3,47 а.е. (11:6) и 3,7 а.е. (5:3). Таким образом, именно резонансы управляют распределением больших полуосей орбит астероидов.

Помимо люков, в поясе астероидов имеются уплотнения, известные как группы или кластеры. Опять же, речь, как правило, идет о скоплениях астероидов вблизи некоторого орбитального расстояния, а не об их реальных группах в каких-то конкретных местах. Однако далее мы рассмотрим два настоящих кластера — это ахейцы (греки) и троянцы. Иногда резонансы приводят к образованию не щелей, а скоплений, и зависит это от тех чисел, которыми выражается резонанс, и некоторых других факторов.