Книга: Естествознание. Базовый уровень. 11 класс

§ 3 Идеальный газ и его законы

§ 3 Идеальный газ и его законы

Изучение тепловых явлений в жидкостях и твёрдых телах часто вызывает затруднения. В этих системах молекулы постоянно взаимодействуют и достаточно прочно удерживаются друг возле друга. Гораздо проще обстоит дело с газами, где молекулы свободно перемещаются и пробегают большие расстояния, а их взаимодействия ограничены только случайными столкновениями. Конечно, в реальных газах приходится учитывать возможную ионизацию и возникающие в результате неё силы электрического притяжения и отталкивания, а также размеры и массу молекул. Однако метод научного абстрагирования оказал науке неоценимую пользу. В своё время Галилей предложил не учитывать влияние трения, затем физики согласились не принимать во внимание размеры тел в уравнениях механики, сводя все их перемещения к движению «материальных точек». Аналогично была создана и модель идеального газа.

Эта модель предполагает, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, а их случайные соударения являются абсолютно упругими. Таким образом, траектория движения каждой молекулы не зависит от движения других молекул. Кроме того, эти молекулы достаточно малы и симметричны, поэтому можно не принимать во внимание их вращение вокруг своей оси. Использование такой модели позволило сформулировать фундаментальные законы, которые во многих случаях достаточно точно объясняют свойства реальных газов.

Три «газовых закона» устанавливают связь между объёмом, давлением и температурой определённой массы газа. Они названы в честь их первооткрывателей законами Бойля – Мариотта, Гей-Люссака и Шарля и являются частными по отношению к уравнению состояния идеального газа[2].

Предположим, что в сосуде находится некоторое количество газа. Данное количество, т. е. суммарную массу всех молекул газа, будем считать постоянным. Это означает, что сосуд является закрытой системой,т. е. газ не выходит из него и не входит в него. Тогда состояние газа можно в полной мере определить с помощью трёх характеристик: занимаемого им объёма, его температуры и давления, которое он оказывает на стенки сосуда. Что такое объём, понятно без дополнительных объяснений. Температура, как мы уже знаем, зависит от средней кинетической энергии всех находящихся в сосуде молекул газа. А что такое давление? Находящиеся в свободном движении молекулы газа время от времени ударяются о стенки сосуда, передавая им свои импульсы. Как вам уже известно, частное от деления изменения импульса на время, в течение которого он действует, представляет собой силу. Таким образом, находящийся в сосуде газ действует на стенки сосуда с некоторой силой. Очевидно, что эта сила пропорциональна площади стенки, так как чем больше площадь, тем больше молекул имеют шанс удариться о неё за единицу времени. Отношение действующей на стенку силы к площади этой стенки, т. е. силу, действующую на единицу площади, называют давлением.

Теперь представим себе довольно простой опыт. Возьмём наполненный воздухом сосуд, одна из стенок которого может быть подвижной. Назовём её поршнем. Поршень должен очень плотно прилегать к стенкам сосуда для того, чтобы избежать утечки воздуха. А для того чтобы не учитывать веса поршня, его надо расположить в вертикальной плоскости. В начале опыта температура и давление в сосуде и в окружающем воздухе одинаковы. Это значит, что за каждый промежуток времени число и сила ударов молекул по поршню с его внутренней стороны будут в среднем такие же, как и с внешней. А если силы давления на поршень с обеих сторон равны, то поршень будет находиться в равновесии, т. е. оставаться на месте. Конечно, он будет совершать небольшие колебания, потому что в какой-то момент в него может случайно ударить изнутри немного больше молекул, чем снаружи, и наоборот. Такие случайные отклонения от равновесия называют флуктуациями. Но поскольку число молекул, ударяющихся в каждый момент о поршень, огромно, такие небольшие отклонения от среднего значения практически невозможно обнаружить.

Теперь приложим к поршню с внешней стороны силу, т. е. начнём толкать его внутрь сосуда. Посмотрим, что произойдёт с заключённым в сосуде газом. Поршень будет перемещаться внутрь сосуда, уменьшая его объём и площадь его стенок. Так как число молекул в сосуде не изменилось, а поверхность стала меньше, то на каждый квадратный сантиметр этой поверхности будет приходиться больше ударов молекул. Следовательно, давление газа в сосуде будет возрастать. Но это ещё не всё. Молекулы, ударяющиеся в движущийся навстречу им поршень, будут отскакивать от него с большей скоростью, чем при ударе о неподвижный. Поэтому скорость молекул в сосуде будет увеличиваться, а, следовательно, температура в нём будет расти. Быстрые молекулы будут ударять в стенки сосуда с большей силой, а это будет служить дополнительной причиной возрастания давления.

Рис. 6. Изотермическое сжатие газа

Таким образом, в рассматриваемом процессе участвуют три взаимозависимых фактора – объём, давление и температура. В этом взаимодействии не так просто разобраться, поэтому авторы законов идеального газа начали с того, что сравнивали их попарно.

Изменение давления и объёма. Попробуем сначала сжимать газ в сосуде таким образом, чтобы температура его при этом не менялась. Это можно сделать, если стенки сосуда хорошо проводят теплоту, а поршень будет двигаться очень медленно. Тогда температура внутри сосуда будет выравниваться с температурой внешней среды и оставаться постоянной. Такой процесс называют изотермическим сжатием (от греч. «изос» – одинаковый и «термо» – температура, теплота). В этом случае увеличение давления будет вызвано только увеличением частоты ударов молекул о стенки сосуда, но не их силой, и поэтому будет пропорционально уменьшению объёма (рис. 6). Эта закономерность отражена в законе Бойля – Мариотта.

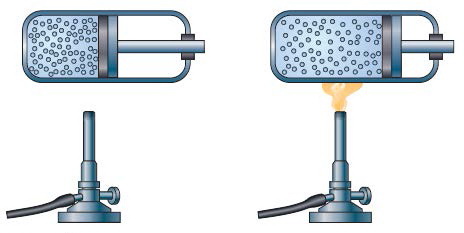
Рис. 7. Изобарическое расширение газа

Изменение объёма и температуры. Теперь посмотрим, как будут связаны между собой объём и температура, если давление останется неизменным. Для этого будем нагревать газ в сосуде с движущимся поршнем. При нагревании кинетическая энергия молекул возрастёт, и вместе с ней возрастёт сила их ударов о поршень. Поскольку теперь на поршень изнутри действует большая сила, чем снаружи, он начнёт выталкиваться из сосуда. Давление в сосуде при этом будет оставаться постоянным, так как усиление ударов молекул компенсируется уменьшением частоты ударов из-за увеличения объёма, а следовательно, и поверхности сосуда (рис. 7). Такой процесс называют изобарическим расширением (от греч. «барос» – тяжесть). Можно также провести изобарическое сжатие. Для этого газ в сосуде надо охладить. Тогда его молекулы будут двигаться медленнее и сила давления наружного воздуха заставит поршень двигаться внутрь сосуда. Давление внутри сосуда при этом, как и прежде, меняться не будет. В этих случаях изменение объёма окажется пропорциональным изменению температуры, что и утверждает закон Гей-Люссака.

Изменение температуры и давления. Выясним, как связаны температура и давление в том случае, когда объём газа остаётся неизменным. Для этого надо закрепить поршень так, чтобы он не мог двигаться, и нагреть сосуд с газом. Поверхность сосуда, а следовательно, и частота ударов молекул о неё меняться не будут, но сила ударов возрастёт из-за увеличения кинетической энергии молекул. В этом случае давление будет увеличиваться пропорционально увеличению температуры, как и утверждает закон Шарля.

А теперь вернёмся к нашему первому опыту, где происходило одновременно изменение объёма, температуры и давления. Эти три величины связывает между собой закон состояния идеального газа, который утверждает, что отношение произведения объёма на давление к абсолютной температуре всегда остаётся постоянным:

pV/T= const,

где p – давление, V – объём сосуда, T – абсолютная температура.

В заключение ещё раз напомним, что все описанные здесь закономерности применимы только к идеальному газу. В реальных газах они соблюдаются с определённым приближением и иногда становятся неверными, особенно в тех случаях, когда, например, температура и давление приобретают очень большие значения.

1. Что представляет собой модель идеального газа?

2. От каких характеристик молекул газа зависит давление на стенки сосуда, в котором он находится?

3. Используя рисунки 6 и 7, расскажите, какие процессы происходят при сжатии газа в закрытом сосуде.

4. Что такое изотермическое и изобарическое расширение?

Проведите исследование. Для этого возьмите пластиковую бутылку из-под любого напитка. Плотно заверните крышку и поместите бутылку в морозильную камеру. Стенки бутылки сожмутся, и объём её уменьшится. Немного нарушьте герметизацию бутылки, слегка отвернув крышку. Вы услышите, как внутрь бутылки входит струя воздуха, а её объём увеличивается. Теперь снимите крышку с бутылки, заткните её комком ваты и поместите в горячую воду. Через некоторое время комок ваты вылетит из бутылки. Объясните все свои наблюдения с точки зрения теплового поведения молекул газа.