Книга: Естествознание. Базовый уровень. 11 класс

§ 8 Энтропия и вероятность

§ 8 Энтропия и вероятность

Итак, что же можно измерить с помощью энтропии? Если бы всё сводилось только к движению молекул и тепловым процессам, понятие энтропии не получило бы такого широкого распространения и популярности и не вышло бы за границы термодинамики.

Энтропию можно использовать при изучении самых различных явлений, а не только тех, которые сводятся к кинетической энергии молекул. Что же именно может характеризовать энтропия в универсальной картине мира? Очевидно, то же самое, что и в термодинамике, – степень беспорядка и хаоса.

Предположим, что у нас имеется некоторое число ячеек, в которые можно помещать одинаковые предметы в любом количестве.

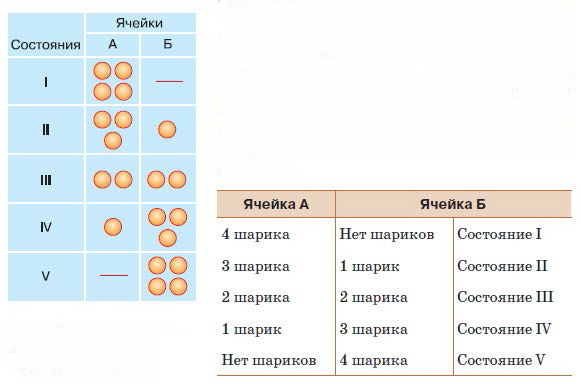
Рис. 17. Схема возможных распределений шариков по ячейкам

В самом простом случае будем иметь дело всего с двумя ячейками и с четырьмя шариками, которые можно произвольно раскладывать по этим ячейкам. Обозначим ячейки как А и Б, а шарики пронумеруем – 1, 2, 3 и 4. Как можно распределить четыре шарика по двум ячейкам? На первом этапе мы не будем принимать во внимание номера шариков, а просто посмотрим, сколько их в каждой ячейке (рис. 17).

Легко убедиться в том, что существует пять вариантов расположения шариков. Обозначим их как состояния I, II, III, IV и V. Теперь обратим внимание на номера шариков и будем учитывать не только, сколько шариков находится в каждой ячейке, но и какие именно шарики там находятся. Мы увидим, что для каждого из состояний существует разное число способов размещения шариков. Состояние I можно осуществить единственным способом, поместив все четыре шарика в ячейку А. Состояние II допускает четыре способа распределения: в ячейке Б может оказаться любой из четырёх шариков. Состояние III (рис. 18) можно реализовать шестью способами. Наконец, состояния IV и V можно осуществить с помощью соответственно четырёх и одного вариантов, так же как и состояния II и I.

А теперь сравним вероятности того, что при случайном перемешивании шариков реализуется какое-либо из пяти возможных макросостояний. Вспомним сведения, которые мы получили ранее. Вероятность события определяется отношением числа благоприятных событий к общему числу возможных событий. В данном случае общее число событий равно 1 + 4 + 6 + 4 + 1 = 16, т. е. четыре шарика можно распределить по двум ячейкам шестнадцатью способами. Поскольку состояния I и V можно реализовать единственным способом, вероятность того, что все шарики окажутся в ячейке А, так же как и вероятность того, что все они попадут в ячейку Б, будет равна ¹?₁₆. Вероятность того, что в ячейке А (или Б) окажется один шарик, а остальные попадут в другую ячейку, равна ⁴/₁₆. Вероятность же того, что шарики расположатся равномерно, по два в каждой ячейке, составит ⁶/₁₆. Можно подсчитать эти вероятности для любого числа ячеек и для любого числа шариков (или молекул), и всякий раз мы будем убеждаться в том, что чем равномернее распределены предметы по ячейкам, тем вероятнее такое распределение. В этом нетрудно убедиться на любом примере. Насыплем в стакан с водой немного сахарного песка.

Сначала наибольшая концентрация сахарного сиропа будет возле дна стакана, но со временем сахар растворится, и концентрация выравняется по всему объёму.

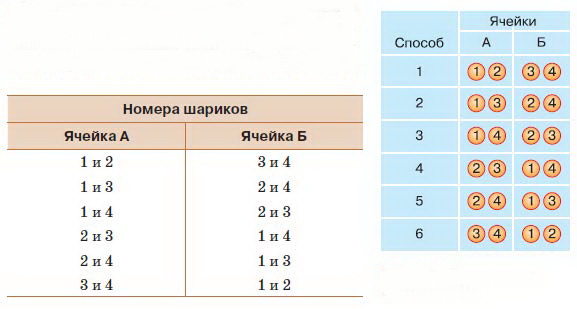
Рис. 18. Реализация состояния III

Представить, что молекулы сахара самопроизвольно соберутся в некоторой части сосуда, практически невозможно, потому что вероятность такого события ничтожно мала.

Таким образом, вероятность состояния с равномерным распределением оказывается наибольшей по сравнению со всеми другими возможными состояниями, и все естественные процессы направлены в сторону достижения этого наиболее вероятного состояния. Но мы также знаем, что в результате всех природных процессов происходит увеличение энтропии. Напрашивается вывод, что между вероятностью существования данного состояния и энтропией должна существовать связь. Эта связь действительно существует, и впервые её охарактеризовал Л. Больцман. Он имел в виду термодинамические процессы, а мы будем рассуждать в рамках наших ячеек и шариков.

Будем называть, как это сделал Больцман, наши состояния I–V макросостояниями. Макросостояние определяется тем, сколько шариков находится в данной ячейке, и не интересуется тем, какие шарики там находятся. В противоположность этому микросостояние определяется тем, какие именно шарики в какой ячейке находятся. Понятно, что, для того чтобы определить микросостояние, требуется более глубокое и внимательное изучение (например, цифры на шариках могут быть едва заметными), поэтому оно так и называется. Разным макросостояниям соответствует различное число микросостояний. Чем более равномерным является распределение шариков по ячейкам, тем больше вероятность такого макросостояния и тем больше микросостояний ему соответствует. Но для такого состояния характерна и наибольшая энтропия. Из этого Больцман сделал вывод, что энтропию данного макросостояния можно измерить числом микросостояний, которым оно определяется. Более точно, энтропия пропорциональна логарифму этого числа. В физике энтропию принято обозначать буквой S, поэтому формулу, выведенную Больцманом, можно представить так:

S = klog W,

где k – коэффициент пропорциональности, а W – число микросостояний, соответствующих данному макросостоянию.

Состояние I, так же как и состояние V, определяется единственным микросостоянием. Так как логарифм единицы по любому основанию равен нулю, то и энтропия этих состояний равна нулю. Это значит, что в этих состояниях существует абсолютный порядок. Число микросостояний, которые определяют макросостояния I и IV, равно четырём, а значит, энтропия каждого из них равна log 4. Величина этого логарифма зависит от того, какое основание для логарифмирования мы выберем. Вообще говоря, основание может быть любым, так как в зависимости от этого изменится только коэффициент пропорциональности. Но по причинам, о которых вы узнаете в дальнейшем, нам будет удобно выбрать основание 2. Тогда энтропия макросостояний I и IV будет равна двум. Самым «беспорядочным» из наших макросостояний будет состояние III, которое может осуществиться шестью микросостояниями. Следовательно, энтропия этого, наиболее вероятного, состояния равна логарифму 6 по основанию 2, что составляет приблизительно 2,6.

1. Что такое макро– и микросостояние?

2. Чему равна энтропия макросостояния, которое обеспечивается единственным микросостоянием?

3. Почему макросостояние, при котором число шариков в каждой ячейке одинаково, оказывается наиболее вероятным?

4. Какие у создателей статистической физики были основания сопоставить вероятность состояния с его энтропией?

Предположим, что у нас имеется 6 шариков, которые могут быть распределены по двум ячейкам.

A. Составьте таблицу, в которой будут указаны все возможные макросостояния.

Б. Составьте таблицу, в которой будут указаны все микросостояния для каждого макросостояния.

B. Найдите вероятность каждого макросостояния.