Книга: Как работает Вселенная: Введение в современную космологию

А.2. ?CDM-модель

А.2. ?CDM-модель

Метрика де Ситтера интересна со многих точек зрения и активно используется в космологии, но она не описывает реальную Вселенную. Причина заключается в том, что наша Вселенная содержит не только космологическую постоянную или темную энергию, но еще и много материи, которая играет важную роль в космологии. Большая ее часть существует в виде небарионной темной материи. Мы также знаем, что эта темная материя движется значительно медленнее скорости света. Такая форма темной материи называется холодной темной материей. Ее давление незначительно по сравнению с плотностью энергии, и она похожа на пылевидную материю, которую мы рассматривали ранее.

Модель, которая включает в себя как космологическую постоянную – ?, так и холодную темную материю – CDM, метко прозвали ?CDM-моделью. Естественно, большая часть обычной барионной материи также холодная и может рассматриваться вместе с холодной темной материей. Мы просто заменим и то и то на пылевидную материю, пока речь идет только о параметрах эволюции Вселенной. При рассмотрении, скажем, барионных акустических колебаний эти виды материи существенно различаются.

Таким образом, мы рассматриваем сферу, заполненную двумя видами материи. Первый из них соответствует пылевидной материи с энергией и плотностью массы ?m = c2?m. Здесь индекс m относится к материи как темной, так и барионной. Ее давление практически отсутствует: pm ? 0. Материя с уравнением состояния p? = –c2?? = –?? заменяет космологическую постоянную и обозначается индексом ?. Как видно из уравнения (2.31), значения этих величин постоянны. В частности, ?? = const. Разделив ?m и ?? на критическую плотность (2.11), мы получаем параметры их плотности ?m и ?? соответственно. Они равны

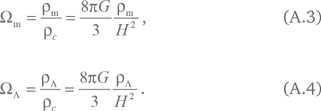
Все три модели Фридмана соответствуют ?? = 0. Случаи замкнутой, плоской и открытой моделей соответствуют ?m > 1, ?m = 1 и ?m < 1. Модель де Ситтера соответствует ?m = 0, ?? = 1.

Параметры плотности и ?m и ?? изменяются с течением времени, потому что постоянная Хаббла зависит от времени, как и плотность вещества (2.8). Значение ?? остается постоянным.

Мы опять выберем произвольную точку отсчета во времени, которую будем считать текущей эпохой, или «сейчас». Все значения, относящиеся к этому моменту, отмечены индексом 0. Например, значение постоянной Хаббла в текущую эпоху – это параметр Хаббла H0, текущий радиус сферы r0, текущая плотность материи ?m0 и т. д. Мы можем выразить плотности материи и космологической постоянной с помощью этих параметров и радиус сферы r с учетом формул (2.8) и (2.35) в виде

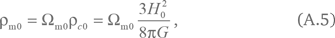
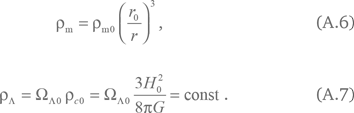
Рассмотрим сферу с двумя видами материи. Пылевидная материя создает ускорение (2.24), а космологическая постоянная создает ускорение (А.1). Вместе они обеспечивают ускорение

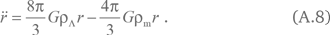
Вычислим значение параметра замедления q (2.23). Мы получаем:

Обратите внимание: мы получили это важное соотношение без использования ОТО. Мы видим, что расширение Вселенной может быть ускоренным или замедленным в зависимости от соотношения между двумя параметрами плотности. Астрономические наблюдения говорят нам, что теперь оно ускоряется, но до того оно замедлялось вплоть до некого момента в прошлом, когда красное смещение составляло около 0,5. Данные спутника «Планк» в сочетании с некоторыми другими наблюдениями обеспечивают текущие значения ?? ? 0,68 и ?m ? 0,32. В соответствии с (A.9) параметр замедления теперь равен q ? 0,32/2 – 0,68 = –0,52.

Воспользуемся (2.12), чтобы найти закон эволюции Вселенной в рамках ?CDM-модели. Мы получаем плотность материи из уравнения (2.8), снабдив величины индексом m: ?m = Br–3. Вместо уравнения (2.12а) получим уравнение, учитывающее влияние космологической постоянной

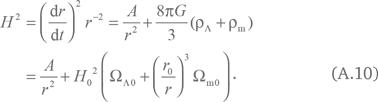
Оно описывает зависимость H(r). Зависимость t(r) имеет вид

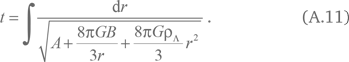
Напомним, что уравнение (2.10) было получено из закона сохранения энергии. Применяя эту интерпретацию к уравнению (А.10), мы видим, что космологическая постоянная вносит в энергию свой вклад, пропорциональный r2, т. е. площади поверхности сферы. Та же зависимость от r будет у энергии поверхностного натяжения сферической оболочки, но с отрицательным коэффициентом поверхностного натяжения. В результате мы пришли к довольно неожиданной нерелятивистской аналогии для космологической постоянной. Эта аналогия, скорее всего, чисто математическая и, вероятно, не имеет особого физического смысла.

Из уравнений (2.11) и (A.10) можно получить обобщение уравнения (2.26) для ?CDM-модели

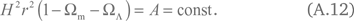
В релятивистской космологии значение 1 – ?m – ?? обозначается ?k и пропорционально пространственной кривизне Вселенной, взятой с обратным знаком. Ее абсолютная величина уменьшается при q < 0. В результате при ускоренном расширении Вселенной она становится все более плоской. Мы уже имели дело с аналогичной ситуацией сразу же после Большого взрыва во время инфляционного расширения Вселенной, которое мы обсуждали в разделе 3.6.