Книга: Достучаться до небес: Научный взгляд на устройство Вселенной

ГЛАВА 17. ВАКАНТНОЕ МЕСТО ТОП–МОДЕЛИ

В январе 2010 г. мои коллеги собрались в Южной Калифорнии на конференцию, чтобы обсудить проблемы физики элементарных частиц и поиск скрытой массы в эпоху БАКа. Организатор конференции Мария Спиропулу — ученый–экспериментатор на CMS и сотрудник физического факультета Калифорнийского технологического института — попросила меня прочитать первую лекцию, рассказать о БАКе и дать обзор основных физических целей на ближайшее будущее.

Мария хотела, чтобы конференция получилась динамичной, и предложила нам начать с «дуэли» между тремя выступающими. Мало того, что термин «дуэль» в применении к трем участникам звучит странно, еще и аудитория с множеством приглашенных гостей оказалась очень сложной — в ней присутствовали как специалисты, так и просто интересующиеся представители научного мира Калтеха. Мария попросила уделить побольше внимания темным моментам современных теорий и экспериментов, причем излагать простым и доступным языком.

Я поступила так, как поступил бы на моем месте любой разумный человек перед лицом таких противоречивых требований: начала тянуть время. Результатом моих изысканий в Сети стал первый слайд презентации (рис. 56); позже Деннис Овербай опубликовал его в The New York Times в своей статье о конференции — вместе с опечаткой в слове «суперсимметрия».

Возле каждого участника «дуэли» (это были я и еще двое выступающих) стояла табличка, из которой было ясно, какую из моделей он намеревается защищать. Все участники конференции, как бы сильно они ни были убеждены в верности своей модели, прекрасно понимали, что в самом ближайшем будущем появятся новые объективные данные, которые и решат вопрос о том, кто будет смеяться последним (или получит Нобелевскую премию).

РИС. 56. Такими я представила модели–кандидаты на слайде для своей презентации

БАК предоставляет нам уникальную возможность получить новые знания и сформировать новые представления о мире. Специалисты в области физики элементарных частиц надеются очень скоро узнать ответы на сложные вопросы, над которыми мы размышляем уже не один десяток лет. Почему частицы обладают массами? Из чего состоит темное вещество? Решают ли дополнительные измерения проблему иерархии? Участвуют ли в этом дополнительные симметрии пространства–времени? Или здесь работает какой?то совершенно неизвестный механизм?

Среди предлагаемых ответов — модели с такими названиями, как суперсимметрия, техницвет и дополнительные измерения. Вообще говоря, ответы могут оказаться далекими от всего, что предлагалось, но эти модели дают нам конкретные цели поиска и говорят о том, на что надо обратить внимание. В этой главе представлено несколько моделей–кандидатов, которые каждая по–своему пытаются решить проблему иерархии; рассказ о них позволит ощутить «аромат» тех исследований, которые будут проводиться на БАКе. Поиск доказательств в пользу всех моделей ведется одновременно; какой бы ни оказалась подлинная теория природы, наши исследования не пропадут даром: в любом случае нас ждут важные открытия.

СУПЕРСИММЕТРИЯ

Начнем, пожалуй, с необычного вида симметрии, известного как суперсимметрия, и моделей с ее участием. Если бы вы провели опрос среди физиков–теоретиков, то значительная их часть сказала бы, что суперсимметрия решает проблему иерархии. А если бы вы опросили экспериментаторов на тему о том, что им больше всего хочется найти, то значительная их часть также назвала бы суперсимметрию.

Еще в 1970–е гг. многие физики уверовали в то, что такие красивые и удивительные теории, так теория суперсимметрии, просто обязаны быть верными, а сама суперсимметрия должна существовать. Более того, они вычислили, что фундаментальные взаимодействия на высоких энергиях в модели суперсимметрии должны действовать с одинаковой силой — и это даже лучше, чем приблизительное соответствие, которое наблюдается в Стандартной модели; в перспективе это допускает объединение взаимодействий.

Многие теоретики также считают, что суперсимметрия — самое убедительное решение проблемы иерархии из всех имеющихся, несмотря на то что согласовать все детали этой теории с уже известными фактами очень трудно.

Суперсимметричные модели предполагают, что у каждой элементарной частицы Стандартной модели — у электронов, кварков и т. п. — имеется партнер в виде частицы с теми же параметрами взаимодействий, но иными квантово–механическими свойствами. Если мир суперсимметричен, то в нем существует множество неизвестных частиц, которые в скором времени могут быть обнаружены: речь идет о суперсимметричных партнерах всех известных частиц (рис. 57).

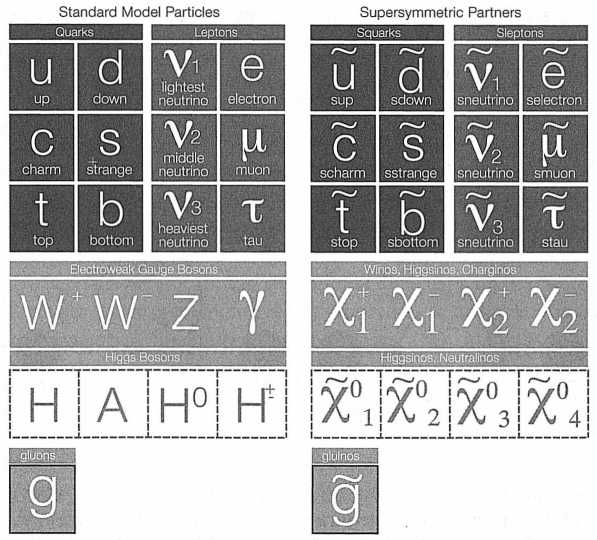
РИС. 57. В теории суперсимметрии у каждой частицы Стандартной модели имеется суперсимметричный партнер, символ которого дополняется значком тильды, а название — у кварков и лептонов — буквой s впереди. Сектор Хиггса в ней также усилен по сравнению со Стандартной моделью

Суперсимметричные модели действительно могли бы помочь в решении проблемы иерархии; если так, они делали бы это весьма примечательным способом. В полностью суперсимметричной модели виртуальный вклад от частиц и их суперсимметричных партнеров в точности компенсируется. Иными словами, если сложить квантово–механический вклад от всех частиц суперсимметричной модели и прибавить получившуюся величину к массе бозона Хиггса, обнаружится, что прибавка в точности равняется нулю. В суперсимметричной модели Хиггс будет легким или вообще безмассовым даже с учетом виртуальных квантово–механических «добавок». В настоящей суперсимметричной теории вклады от обоих типов частиц полностью компенсируются (рис. 58).

Квантовая механика делит вещество на две очень разные категории — бозоны и фермионы. Фермионы — это частицы, обладающие массой. Возможно, это заявление кажется фантастическим, но в действительности компенсация добавок массы гарантируется, потому что суперсимметрия представляет собой совершенно особый вид симметрии. Это симметрия пространства и времени — она напоминает знакомые виды симметрии, такие как симметрия вращения и параллельного переноса, но расширяет их в квантово–механическую область.

РИС. 58. В суперсимметричной модели вклад в массу бозона Хиггса от суперсимметричных частиц в точности компенсирует вклад от частиц Стандартной модели. К примеру, на двух приведенных здесь диаграммах сумма виртуальных вкладов равняется нулю

ющие полуцелым собственным моментом импульса, где момент импульса — это квантовое число, которое описывает поведение частицы, которое в определенном смысле можно уподобить ее вращению. Под полуцелым моментом импульса подразумеваются величины вроде 1/2, 3/2, 5/2 и т. д. Примеры фермионов — кварки и лептоны Стандартной модели: их момент импульса равен 1/2. Бозоны — это частицы, которые, подобно переносящим взаимодействие калибровочным бозонам или ожидающему своего открытия бозону Хиггса, имеют суммарный момент импульса, выражаемый целыми числами, такими как 0,1, 2 и т. д.

Фермионы и бозоны различаются не только моментами импульса. Они очень по–разному себя ведут, когда в одном месте оказывается две или более одинаковые частицы. К примеру, идентичные фермионы с одинаковыми свойствами невозможно обнаружить в одном месте. Об этом говорит нам принцип исключения, или запрет Паули, названный в честь австрийского физика Вольфганга Паули. Именно этим свойством фермионов объясняется структура периодической системы Менделеева, основанная на том, что электроны, которые не отличаются друг от друга ни по одному квантовому числу, должны находиться на разных орбитах вокруг атомного ядра. По этой же причине мой стул не проваливается в центр Земли — фермионы стула просто не могут находиться в том же месте, что фермионы вещества планеты.

Бозоны же ведут себя строго противоположным образом. Их как раз вероятнее найти в одном месте. Они могут буквально громоздиться один на другой — примерно как крокодилы; именно поэтому могут существовать такие явления, как бозе–конденсат, где частицы должны находиться в одинаковом квантово–механическом состоянии. В лазерах тоже используется бозонное родство фотонов. Интенсивный луч лазера состоит из множества идентичных фотонов.

Интересно, что в суперсимметричной модели частицы, которые мы считаем очень разными, — бозоны и фермионы — можно заменить на противоположные, и в результате получится ровно то же, с чего все началось. У каждой частицы есть партнер противоположного квантово–механического типа, обладающий в точности такими же зарядами и массой и отличающийся только моментом импульса. Названия новых частиц звучат довольно забавно — на лекциях они обязательно вызывают смешки в аудитории. К примеру, партнером фермионного электрона является бозонный селектрон. Бозонный фотон состоит в паре с фермионным фотино, а W–бозон спарен с Wino–фермионом. Новые частицы взаимодействуют между собой подобно соответствующим частицам Стандартной модели, но при этом обладают противоположными квантово–механическими свойствами.

В суперсимметричной теории свойства каждого бозона сопоставлены свойствам его суперпартнера–фермиона, и наоборот. Поскольку у каждой частицы есть суперпартнер, и все взаимодействия между ними строго сбалансированы, теория допускает существование столь причудливой симметрии, которая заменяет фермионы бозонами, и наоборот.

Чтобы понять загадочную на первый взгляд взаимную компенсацию виртуальных вкладов в массу хиггса, следует вспомнить, что суперсимметрия подбирает каждому бозону соответствующий партнер–фермион. В частности, бозону Хиггса в этой модели ставится в соответствие фермион Хиггса, или хиггсино. Если на массу бозона квантово–механические добавки оказывают существенное влияние, то масса фермиона не может быть много больше его классической массы, то есть массы без учета квантово–механических поправок.

Логика здесь заложена довольно тонкая, но большие поправки не возникают, потому что массы фермионов относятся как к правым, так и к левым частицам. Масса позволяет им превращаться друг в друга и обратно. Если классического массового члена нет и частицы не могут превращаться друг в друта до прибавления квантово–механических виртуальных эффектов, то они не смогут сделать этого и после учета всех квантово–механических вкладов. Если фермион с самого начала не имеет массы (то есть не имеет классической массы), то его масса останется нулевой и после включения квантово–механических поправок.

К бозонам подобные аргументы не применимы. Бозон Хиггса, к примеру, имеет нулевой собственный момент импульса, так что ни в каком смысле мы не можем говорить о том, что он вращается влево или вправо. Но из соображений суперсимметрии массы бозонов соответствуют массам фермионов. Поэтому если масса хиггсино равна нулю (или мала), точно такой же должна быть согласно теории суперсимметрии масса его партнера — бозона Хиггса — даже с учетом квантово–механических поправок.

Мы пока не знаем, верно ли это довольно изящное объяснение стабильности иерархии и компенсации поправок к массе хиггса. Но если суперсимметрия действительно решает проблему иерархии, то мы многое можем сказать о том, каких результатов следует ожидать на БАКе. В этом случае мы знаем, какие именно новые частицы должны существовать, потому что у каждой известной частицы должен быть суперсимметричный партнер. Мало того, мы можем оценить массы новых частиц.

Разумеется, если бы суперсимметрия в природе соблюдалась в точности, мы бы сразу знали и массы всех суперпартнеров. Они были бы попросту идентичны массам соответствующих известных частиц. Однако ни одну частицу–суперпартнер до сих пор обнаружить не удалось. Это свидетельствует о том, что суперсимметрия, даже если она реально существует в природе, не может быть строгой. При строгой суперсимметрии мы давно уже открыли (>ы и селектрон, и скварки, и все остальные суперсимметричные партнеры, предсказанные теорией.

Так что суперсимметрия должна нарушаться в том смысле, что отношения, предсказанные теорией суперсимметрии, не могут быть строгими. Согласно теории нарушенной суперсимметрии у каждой частицы по–прежнему есть суперпартнер, но массы этих суперпартнеров отличаются от масс оригинальных частиц Стандартной модели.

Однако если суперсимметрия нарушена слишком сильно, она не сможет разрешить проблему иерархии, потому что мир при сильно нарушенной симметрии выглядит в точности так же, как если бы этой симметрии вовсе не было. Суперсимметрия должна быть нарушена ровно настолько, чтобы мы до сих пор не могли наблюдать ее признаков, но чтобы масса Хиггса была тем не менее защищена от больших квантово–механических вкладов, которые сделали бы ее слишком большой.

Это говорит о том, что суперсимметричные частицы должны иметь массы масштаба слабого взаимодействия. Будь они легче — и мы бы их уже обнаружили; будь они тяжелее — и следовало бы ожидать более тяжелого хиггса. Мы не можем точно сказать, какими будут эти массы, ведь и масса Хиггса известна нам лишь очень приблизительно. Но мы знаем, что если эти массы окажутся слишком большими, то проблема иерархии никуда не денется.

Поэтому мы делаем вывод о том, что если суперсимметрия существует в природе и решает проблему иерархии, то должно существовать множество новых частиц с массами в диапазоне от нескольких сотен гигаэлектронвольт до нескольких тераэлектронвольт. Это именно тот диапазон, в котором БАК должен будет вести поиск. При энергии столкновения 14 ТэВ коллайдер должен выдавать эти частицы даже с учетом того, что кваркам и глюонам, порождающим при столкновении новые частицы, достается лишь небольшая часть исходной энергии протонов.

Проще всего будет получить на БАКе суперсимметричные частицы, несущие сильный (или цветовой) заряд. Эти частицы при столкновении протонов (или, точнее, при столкновении кварков и глюонов в них) могут рождаться в изобилии. Иными словами, при штатной работе БАКа могут возникать новые суперсимметричные частицы, участвующие в сильном взаимодействии. Если это так, они оставят в детекторах очень заметные и характерные следы.

Эти сигнатуры — экспериментальные свидетельства, оставляемые частицей — зависят от того, что происходит с частицей после возникновения. Большинство суперсимметричных частиц будут быстро распадаться. Причина в том, что, как правило, для каждой такой тяжелой частицы существует более легкая частица (такая как частицы Стандартной модели) с точно таким же полным зарядом. Если это так, то тяжелая суперсимметричная частица распадется на частицы Стандартной модели таким образом, чтобы сохранился первоначальный заряд, и эксперимент обнаружит только частицы Стандартной модели.

Вероятно, этого недостаточно, чтобы распознать суперсимметрию. Однако почти во всех суперсимметричных моделях суперсимметричная частица не может распадаться исключительно на частицы Стандартной модели. После ее распада должна остаться другая (более легкая) суперсимметричная частица. Причина в том, что суперсимметричные частицы появляются (или исчезают) только парами. Поэтому на месте распада одной суперсимметричной частицы должна остаться другая суперсимметричная частица. Следовательно, самая легкая из таких частиц должна быть стабильной. Эта самая легкая частица, которой не на что распадаться, известна физикам как легчайшая суперсимметричная частица, или LSP.

С экспериментальной точки зрения распад суперсимметричной частицы характерен тем, что даже после завершения всех процессов легчайшая из нейтральных суперсимметричных частиц должна остаться. Космологические ограничения говорят о том, что LSP не несет никаких зарядов и потому не будет взаимодействовать ни с одним из элементов детектора. Это означает, что в каждом случае возникновения и распада любой супер- симметричной частицы экспериментальные результаты покажут, что импульс и энергия не сохраняются, их часть куда?то пропадает. Частица LSP уйдет незамеченной и унесет свои импульс и энергию туда, где их невозможно будет зарегистрировать; сигнатурой LSP будет дефицит энергии.

Предположим, к примеру, что в результате столкновения возникает скварк — суперсимметричный партнер кварка. На какие частицы он распадется, зависит от его массы и от того, какие имеются более легкие частицы. Одним из возможных вариантов распада будет превращение скварка в обычный кварк и легчайшую суперсимметричную частицу (рис. 59). Напомню, что распад может происходить практически немедленно, и детектор зарегистрирует только его продукты. Если произошел распад скварка, детекторы зарегистрируют пролет кварка в трекере и в адронном калориметре, который измеряет энергию, отдаваемую частицами, участвующими в сильном взаимодействии, но установка определит также недостачу части импульса и энергии. Тот факт, что импульса не хватает, экспериментаторы определят точно так же, как и при рождении нейтрино. Они измерят весь поперечный по отношению к пучку импульс и обнаружат, что в сумме он не равен нулю.

Одна из сложнейших задач, стоящих перед экспериментаторами, — достоверно и однозначно распознать недостачу импульса. В конце концов, все незарегистрированное будет казаться пропавшим! Если что?то пойдет не так или будет измерено неверно, а в результате уйдет незамеченной хотя бы крохотная доля энергии, то недостающий импульс создаст полную картину улетевшей суперсимметричной частицы, хотя на самом деле ничего особенного при столкновении не возникло.

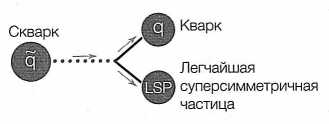
РИС. 59. Скварк может распадаться на кварк и легчайшую суперсимметричную частицу

Разумеется, скварк никогда не возникает сам по себе, а только вместе с другим объектом, также участвующим в сильном взаимодействии (к примеру, с другим скварком или антискварком), поэтому экспериментаторы зарегистрируют и измерят по крайней мере две струи (пример см. на рис. 60). Если при столкновении протонов возникли два скварка, при распаде они породят два кварка, которых зарегистрируют детекторы. Часть энергии и импульса уйдут из системы с двумя LSP, и само их отсутствие будет свидетельствовать о возникновении новых частиц.

Как ни странно, долгие задержки с пуском БАКа сыграли и положительную роль: они дали экспериментаторам время как следует разобраться в своих детекторах. Их удалось заранее откалибровать, так что с первого дня работы коллайдера измерения будут чрезвычайно точными, а данные об упущенной энергии — надежными. Теоретики, с другой стороны, получили время обдумать альтернативные стратегии поиска для суперсимметричной и других моделей. К примеру, мне вместе с Дейвом Таккер–Смитом, ученым из Колледжа Уильямса, удалось найти отличный от вышеописанного — но родственный — способ поиска скварка. Наш метод опирается на измерение только импульса и энергии получающихся кварков; в нем не нужно точно измерять недостающий импульс (а это очень непросто и не дает надежных результатов). Метод вызвал среди ученых БАКа заметное оживление; экспериментаторы CMS сразу же приняли его и не только показали, что метод работает, но и в течение всего нескольких месяцев обобщили и улучшили его. Теперь это часть стандартной стратегии поиска суперсимметрии; метод, предложенный нами так недавно, был использован в первом же сеансе поиска суперсимметрии на CMS.

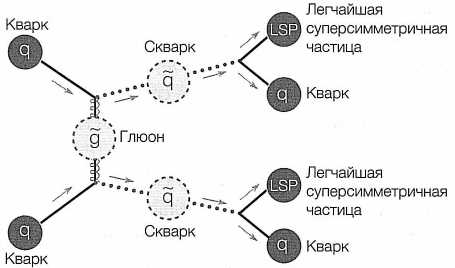
РИС. 60. Два скварка, одновременно возникшие в БАКе, распадутся на кварк и LSP каждый и оставят после себя сигнатуру в виде дефицита энергии

Если суперсимметрия будет обнаружена, экспериментаторы на этом не остановятся. Они попытаются определить весь спектр суперсимметричных частиц, а теоретики будут работать над интерпретацией полученных результатов. Под идеей суперсимметрии и частиц, способных вызывать ее спонтанное нарушение, скрывается интереснейшая теория. Мы знаем, какие суперсимметричные частицы должны существовать, если суперсимметрия существенна для проблемы иерархии, но мы пока не знаем ни их точных масс, ни того, как эти массы возникают.

То, что увидит БАК, очень сильно зависит от спектра масс суперсимметричных частиц, который, вероятно, отличается от спектра масс обычных частиц. Мы знаем, что частицы могут распадаться только на более легкие. Цепочка распадов — последовательность возможных распадов суперсимметричных частиц — определяется их массами, тем, какие из них легче, а какие тяжелее. Скорости различных процессов также зависят от массы частиц. Более тяжелые частицы в среднем распадаются быстрее. Кроме того, их обычно сложнее получить, потому что они возникают только при высокоэнергетических столкновениях. Все это дало бы нам важную информацию о том, что лежит в основе Стандартной модели и что ожидает нас на следующих энергетических масштабах. Естественно, это относится к анализу любых новых данных, которые нам удастся получить.

Тем не менее следует помнить, что, несмотря на популярность теории суперсимметрии среди физиков, существует несколько поводов для беспокойства и оснований сомневаться в том, что эта теория действительно применима в реальном мире и решает проблему иерархии.

Во–первых, и это, возможно, самое главное, мы пока не видели никаких экспериментальных свидетельств в пользу этой теории. Если суперсимметрия существует, то единственным оправданием для полного отсутствия доказательств может быть тот факт, что все суперпартнеры тяжелые. Но естественное решение проблемы иерархии требует, чтобы суперпартнеры были относительно легкими. Чем тяжелее суперпартнеры, тем менее адекватным средством решения проблемы иерархии представляется суперсимметрия. Потребуется подгонка, определяемая отношением массы бозона Хиггса к масштабу масс, при которых нарушается суперсимметрия. Чем больше это отношение, тем сильнее придется «настраивать» теорию.

В суперсимметричной модели есть единственный способ сделать Хиггса достаточно тяжелым, чтобы его не обнаружили до сих пор, а именно — включить в его массу значительные квантовомеханические поправки, для которых опять же необходимы тяжелые суперпартнеры. Их массы должны быть настолько большими, что естественное решение проблемы иерархии вновь невозможно, несмотря на суперсимметрию.

Еще одна проблема с суперсимметрией — проблема поиска непротиворечивой модели, которая предусматривала бы нарушение суперсимметрии и была согласована со всеми полученными до сего дня экспериментальными данными. Суперсимметрия — очень специфическая симметрия, она устанавливает связи между многими взаимодействиями и запрещает некоторые из них, которые, вообще говоря, квантовая механика допускает. При нарушении суперсимметрии берет верх «принцип анархии» и все, что может случиться, случается. Большинство моделей предсказывают типы распадов, которые либо никогда не регистрировались в эксперименте, либо встречаются слишком редко по сравнению с прогнозом. В общем, стоит суперсимметрии нарушиться, и квантовая механика не упустит случая разворошить осиное гнездо.

Возможно, физики просто не замечают верных ответов. Мы, разумеется, не можем точно сказать, что хороших моделей не существует или что некоторой подгонки не потребуется. Конечно, если суперсимметрия — верное решение проблемы иерархии, то доказательства ее существования скоро будут получены на БАКе. Так что этот вариант, безусловно, стоит исследовать. Открытие суперсимметрии означало бы, что эта новая симметрия пространства–времени применима не только в теоретических изысканиях, но и в реальном мире.

Однако пока суперсимметрия не доказана, имеет смысл рассмотреть и альтернативные варианты. И первой в очереди стоит модель, известная как техницвет.

ТЕХНИЦВЕТ

Еще в 1970–е гг. физики рассматривали и альтернативную гипотезу решения проблемы иерархии, известную как теория техницвета. В моделях этого класса фигурируют частицы, которые интенсивно взаимодействуют между собой посредством новой силы, получившей шутливое название техницветной. Суть идеи состояла в том, что сила эта действует примерно так же, как сильное взаимодействие (известное в среде физиков еще и как цветовое взаимодействие), но связывает между собой частицы на масштабе энергий, характерном для слабого взаимодействия, а не на намного более низком уровне протонных масс.

Если ответом на проблему иерархии действительно является техницвет, то БАК не произведет на свет ни одного фундаментального бозона Хиггса. Вместо этого он выдаст некое связанное состояние — что?то похожее на адрон, которое будет играть роль частицы Хиггса. Экспериментальным свидетельством в пользу техницвета будет множество сложных частиц (связанных состояний) и сильных взаимодействий — все очень похоже на привычные адроны, но только на гораздо более высоком уровне энергий на масштабе слабого взаимодействия или даже выше.

Однако если решение проблемы иерархии — действительно техницвет, то мы должны были бы уже обнаружить тому доказательства, хотя, конечно, могли и пропустить что?то не слишком заметное.

Кроме того, строить модели на базе теории техницвета еще сложнее, чем на основе суперсимметрии. Оказалось, что найти модель, которая согласовывалась бы со всем, что мы наблюдаем в природе, — очень нетривиальная задача, и до сих пор подобрать полностью подходящую модель не удалось.

Тем не менее экспериментаторы будут работать непредвзято; поиск техницветной силы и любого другого нового типа сильного взаимодействия тоже входит в программу, но надежды на положительный результат не слишком велики. Однако если окажется все?таки, что именно теория техницвета лежит в фундаменте нашего мироустройства, то, может быть, Microsoft Word перестанет наконец воспринимать это слово только как название запатентованного полиграфического процесса и исправлять первую его букву на заглавную.

ДОПОЛНИТЕЛЬНЫЕ ИЗМЕРЕНИЯ

Ни суперсимметрия, ни техницвет не дают нам идеального решения проблемы иерархии. Суперсимметричные теории не предлагают нам экспериментально непротиворечивых механизмов нарушения суперсимметрии, а создать на основе техницветной силы теорию, которая предсказывала бы правильные массы для кварков и лептонов, еще сложнее. Поэтому физики решили отойти от шаблонов и рассмотреть идеи, на первый взгляд еще более неоднозначные. Не забывайте, что даже если теория кажется поначалу нелепой, это ничего не значит. Только после того как полностью разберемся в ее следствиях, мы сможем решить, какая из идей самая красивая и, что гораздо важнее, правильная.

Лучшее понимание теории струн и ее компонентов, которого физики добились в 1990–е гг., позволило создать новые подходы к решению проблемы иерархии. На новые идеи физиков вдохновили элементы теории струн, хотя и не обязательно непосредственно следующие из ее очень ограниченной структуры, и речь в них идет о дополнительных пространственных измерениях. Если дополнительные измерения существуют — а у нас есть основания предполагать, что они могут существовать, — то именно в них может скрываться ключ к решению проблемы иерархии. Если это действительно так, то экспериментальных доказательств тоже можно ждать от БАКа.

Дополнительные пространственные измерения — концепция довольно экзотическая. Если во Вселенной действительно есть такие измерения, то пространство вокруг нас на самом деле совсем не такое, каким мы его наблюдаем в повседневной жизни. Помимо обычных трех измерений — лево–право, верх–низ, вперед–назад (длина, ширина и высота, иначе говоря) — пространство продолжается также в иных, невидимых направлениях.

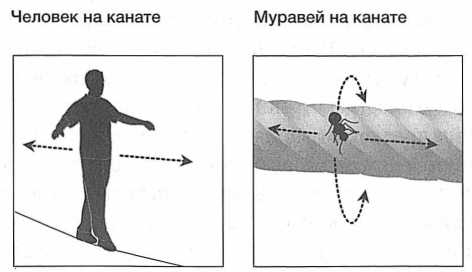
РИС. 61. Человек и крохотный муравей воспринимают натянутый канат очень по–разному. Для человека он имеет лишь одно измерение, для муравья — два

Почему мы не видим этих измерений? Причина может заключаться в том, что они слишком малы, чтобы непосредственно влиять на что?либо из того, что мы можем наблюдать; это предположил физик Оскар Клейн еще в 1926 г. Идея в том, что из?за ограниченных возможностей нашего восприятия некоторые измерения могут оказаться слишком маленькими и потому неразличимыми для нас. Так, гимнаст, идущий по канату, видит свой путь одномерным, тогда как крохотный муравей на том же канате может двигаться в двух измерениях (рис. 61).

В другом варианте измерения могут быть скрытыми потому, что пространство–время изогнуто или скручено — как и должно происходить по Эйнштейну в присутствии энергии. Если искривление достаточно сильное, то эффекты дополнительных измерений незаметны, как определили в 1999 г. мы с Раманом Сандра- мом. Это означает, что геометрия свернутого пространства также позволяет измерениям «прятаться».

Но почему у ученых вообще возникла мысль о каких бы то ни было дополнительных измерениях, если никто никогда ничего подобного не видел? В истории физики такое происходило не раз. Никто до поры до времени не «видел» атомы и никто не «видел» кварки. Тем не менее сегодня у нас полно экспериментальных доказательств существования и того и другого.

Никакие законы физики не утверждают, что пространственных измерений может быть только три. Общая теория относительности Эйнштейна работает при любом числе измерений. Более того, вскоре после того как Эйнштейн завершил свою теорию гравитации, Теодор Калуца расширил его идеи и предположил существование четвертого пространственного измерения, а еще через пять лет Оскар Клейн предложил вариант того, как это измерение может быть свернуто и чем оно должно отличаться от трех привычных.

Теория струн — ведущий кандидат на роль теории, объединяющей гравитацию и квантовую механику, — является еще одной причиной того, что физики сейчас всерьез думают о дополнительных измерениях. Теория струн не включает в себя очевидным образом ту теорию гравитации, с которой мы знакомы. Для этого ей необходимы дополнительные измерения.

Меня часто спрашивают, сколько всего измерений существует во Вселенной. Этого мы не знаем. Теория струн предполагает шесть или семь дополнительных измерений. Но создатели моделей на этом не останавливаются. Вполне возможно, что разные варианты теории струн дадут разные ответы на этот вопрос. Во всяком случае, авторов представленных в этой главе моделей интересуют только те измерения, которые в достаточной мере искривлены или настолько велики, что могут оказывать влияние на физические предсказания. Могут существовать и другие измерения, слишком маленькие даже для физики элементарных частиц, но мы не будем принимать в расчет подобные сверхмалые сущности. Вспомним, что такое эффективная теория, и забудем обо всем слишком мелком или невидимом — о том, что не оказывает на нашу систему никакого измеримого воздействия.

Кроме того, теория струн вводит новые элементы, а именно браны; их назначение — обеспечить геометрии Вселенной дополнительные возможности в том случае, если она действительно содержит дополнительные измерения. В 1990–е гг. физик–теоретик, специалист по теории струн Джо Полчински установил, что теория струн — это не просто теория одномерных объектов. Вместе с коллегами он продемонстрировал, что для этой теории также принципиально важны многомерные объекты, известные как браны.

«Брана» происходит от слова «мембрана». Подобно мембранам, которые представляют собой двумерные поверхности в трехмерном пространстве, браны в многомерном пространстве — это поверхности с меньшим числом измерений. Браны способны захватывать в ловушку частицы и силы, так что те теряют способность передвигаться по пространству полной размерности. Браны в многомерном пространстве похожи на занавеску у вас в ванной, которая представляет собой двумерную поверхность в трехмерной комнате (рис. 62). Как капли воды могут двигаться только по двумерной поверхности оконного стекла, так и частицы и силы могут оказаться заперты на «поверхности» браны с меньшим числом измерений, чем в окружающем пространстве.

Можно сказать, что существует два типа струн: открытые струны, у которых есть концы, и замкнутые струны, образующие кольца вроде аптечных резинок (рис. 63). В 1990–е гг. струнники–теоретики поняли, что концы открытых струн не могут находиться где попало — струны должны начинаться и заканчиваться на бранах. Частицы, возникающие из колебаний открытой струны, прикрепленной к бране, тоже оказываются запертыми на ней. Частицы, представляющие собой колебания этих струн, не могут никуда уйти с браны. Как капли на окне, они могут передвигаться в пределах измерений браны, но не могут ее покинуть.

РИС. 62. Брана захватывает в ловушку частицы и силы, которые могут двигаться вдоль нее, но не в состоянии ее покинуть — примерно как капли воды на занавеске в душе

РИС. 63. Открытая струна с двумя концами и замкнутая бесконечная струна

Теория струн предполагает, что существует множество типов бран, но для моделей, пытающихся разрешить проблему иерархии, больше всего интересны те, что распространяются на три измерения — те самые три физических измерения пространства, которые нам известны. Частицы и силы могут быть заперты на такой бране, при том что пространство и тяготение охватывают больше измерений (на рис. 64 схематично представлен мир браны, где человек и магнит ограничены измерениями браны, а гравитация действует как на ней, так и за ее пределами).

Дополнительные измерения теории струн в принципе могли бы оказывать физическое влияние на наблюдаемый мир, как и трехмерные браны. Возможно, важнейшая причина рассматривать дополнительные измерения заключается в том, что они могут влиять на видимые явления и, в частности, объяснять серьезнейшие загадки, такие как проблема иерархии в физике элементарных частиц. Дополнительные измерения и браны могут оказаться ключом к решению этой проблемы; возможно, они помогут понять, почему гравитация так слаба.

Это возвращает нас к главной причине обращения к многомерным моделям и дополнительным пространственным измерениям. Они могут оказывать влияние на явления, в которых мы сейчас пытаемся разобраться, и если это так, то не исключено, что доказательства их существования появятся в самом ближайшем будущем.

Напомню, что проблему иерархии можно сформулировать двумя разными способами. Можно описать суть вопроса тем, что масса хиггсовой частицы — и, соответственно, масштаб слабого взаимодействия — на много порядков меньше массы Планка. Именно этот вопрос мы рассматривали, говоря о суперсимметрии и тех- ницветной силе. Но можно задать и эквивалентный вопрос: а почему гравитация так слаба по сравнению с другими известными фундаментальными взаимодействиями? Сила тяготения определяется планковским масштабом — громадной массой, в десять тысяч триллионов раз превышающей массу слабого взаимодействия. Чем больше масса Планка, тем слабее сила тяготения. Только когда масса объектов достигает или почти достигает планковского масштаба, сила тяготения становится существенной. А до тех пор пока частицы намного легче и не подходят под масштаб, заданный массой Планка (как, собственно, и обстоит дело в нашем мире), сила тяготения остается чрезвычайно слабой.

РИС. 64. Частицы и взаимодействия Стандартной модели могут быть заперты в мире браны, существующей в многомерном пространстве. В этом случае все вокруг — мои знакомые, вещество и известные нам звезды, взаимодействия, такие как электромагнетизм, наша Галактика и Вселенная — существует в привычных трех измерениях. Гравитация, с другой стороны, распространяется на все пространство. (Фото публикуется с разрешения Марти Розенберга.)

Загадка, связанная со слабостью гравитационных сил, по существу эквивалентна проблеме иерархии — решение одной решает и другую. Но формулировка проблемы иерархии в терминах гравитации помогает думать о решениях, связанных с дополнительными измерениями. А нам пора познакомиться с парой наводящих вопросов.