Книга: Достучаться до небес: Научный взгляд на устройство Вселенной

В ПОИСКАХ ПЕРЕНОСЧИКОВ СЛАБОГО ВЗАИМОДЕЙСТВИЯ

В ПОИСКАХ ПЕРЕНОСЧИКОВ СЛАБОГО ВЗАИМОДЕЙСТВИЯ

Прежде чем закончить разговор о том, как распознаются частицы Стандартной модели, рассмотрим последнюю их группу — слабые калибровочные бозоны: два W и один ?, переносящие слабое ядерное взаимодействие. Слабые калибровочные бозоны отличаются той особенностью, что, в отличие от фотонов и глюонов, имеют ненулевую массу покоя. Надо сказать, что наличие массы у слабых калибровочных бозонов — частиц, передающих слабое взаимодействие — представляет собой достаточно серьезную фундаментальную загадку. Происхождением своим эти массы — как и массы других элементарных частиц, о которых говорилось в этой главе — обязаны механизму Хиггса, к которому мы перейдем в самом ближайшем будущем.

Из?за своей тяжести W- и ?–бозоны долго не живут; они распадаются. Это значит, что слабые калибровочные бозоны, подобно истинным кваркам и другим тяжелым нестабильным частицам, можно распознать только через наблюдение за частицами, рождающимися в процессе распада. А поскольку любые новые тяжелые частицы тоже, вероятно, окажутся нестабильными, мы попробуем на примере распада слабых калибровочных бозонов показать еще одно интересное свойство распадающихся частиц.

W–бозон взаимодействует с любыми частицами, чувствительными к слабому взаимодействию (то есть со всеми частицами, о которых до сих пор шла речь). Это дает W–бозону множество вариантов распада. Он может распасться на любой заряженный лептон (электрон, мюон или тау–частицу) и соответствующее ему нейтрино. Его распад может также породить пару кварков — верхний и нижний или очарованный и странный, как показано на рис. 44.

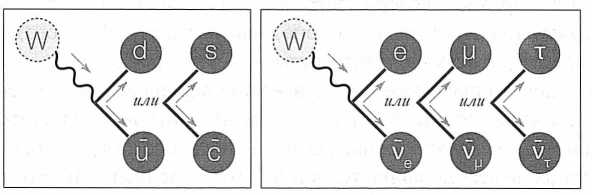
РИС. 44. W–бозон может распасться на любой заряженный лептон и соответствующее ему нейтрино, или на верхний и нижний кварки, или на очарованный и странный кварки. На самом деле в кварковом секторе имеется смешивание, так что W–бозон может иногда распадаться в кварки разных поколений

Возможные варианты распада, помимо всего прочего, зависят от массы исходной частицы. Дело в том, что продукты распада частицы в сумме должны давать массу, меньшую, чем масса исходной частицы. Так, хотя W–бозон вполне способен взаимодействовать с истинным и красивым кварками, распасться на них он не может, так как масса истинного кварка больше массы W–бозона[48].

Рассмотрим распад W–бозона на два кварка, поскольку в этом случае экспериментаторы могут измерить оба продукта распада (в случае лептона и нейтрино это не так, потому что нейтрино не посредственно не обнаруживается). По закону сохранения энергии и импульса суммарная энергия и импульс конечных кварков равны энергии и импульсу распавшейся частицы, то есть W–бозона.

В этот момент, однако, вмешиваются специальная теория относительности Эйнштейна и квантовая механика, и ситуация становится более интересной. Специальная теория относительности говорит нам о том, как соотносятся масса, энергия и импульс. Большинству людей знаком сокращенный вариант формулы Е = mc². Эта формула верна для частиц в состоянии покоя; здесь т интерпретируется как т₀ — неисчезающая масса покоя частицы, изначально ей присущая. Если частица движется, у нее имеется импульс, и на сцене появляется более полная формула: Е²–р²с²= т₀²с². По этой формуле[49] экспериментаторы могут вычислить массу частицы даже в том случае, если сама она давно распалась. Для этого достаточно измерить суммарный импульс и энергию продуктов распада и, применив это уравнение, вычислить массу первоначальной частицы.

Причина, по которой в этой истории фигурирует квантовая механика, несколько тоньше. Если наблюдать со стороны, то масса частицы не всегда равняется в точности ее реальной и истинной массе. Частицы способны распадаться, а квантово–механическое уравнение неопределенности говорит нам, что для точного измерения энергии необходимо бесконечное время; это значит, что энергию частицы, имеющей ограниченный срок жизни, вообще невозможно знать точно. Величина возможной ошибки тем больше, чем быстрее распадается частица и чем меньше время ее жизни. Следовательно, в любом конкретном измерении можно получить значение массы, близкое, но не равное ее истинному среднему значению. Только проведя множество измерений, экспериментаторы могут выяснить одновременно массу—наиболее вероятную ее величину, к которой сходится среднее значение — и время жизни, поскольку именно продолжительность существования частицы до распада определяет разброс измеренных масс (рис. 45). Это верно не только для W–бозона, но и для любой другой распадающейся частицы.

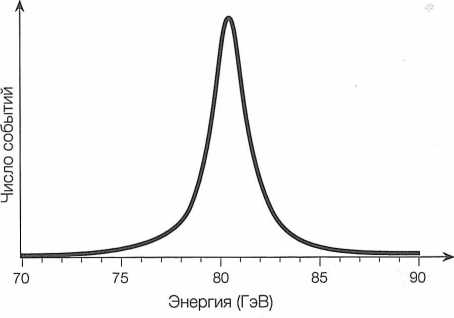
РИС. 45. Измерения массы нестабильной частицы концентрируются вокруг ее истинной массы, но допускают некоторый разброс в зависимости от времени жизни. На рисунке показана соответствующая зависимость для калибровочного W–бозона

Разобравшись в полученных измерительных данных при помощи описанных в этой главе методов, экспериментаторы могут обнаружить какую?нибудь частицу Стандартной модели (см. на рис. 46 сводку частиц Стандартной модели и их свойств)[50], а может, и что?нибудь совершенно новое. Ученые надеются получить на БАКе новые экзотические частицы, которые помогут глубже проникнуть в фундаментальную природу вещества или даже Вселенной в целом. В следующей части книги мы рассмотрим некоторые интересные возможности.

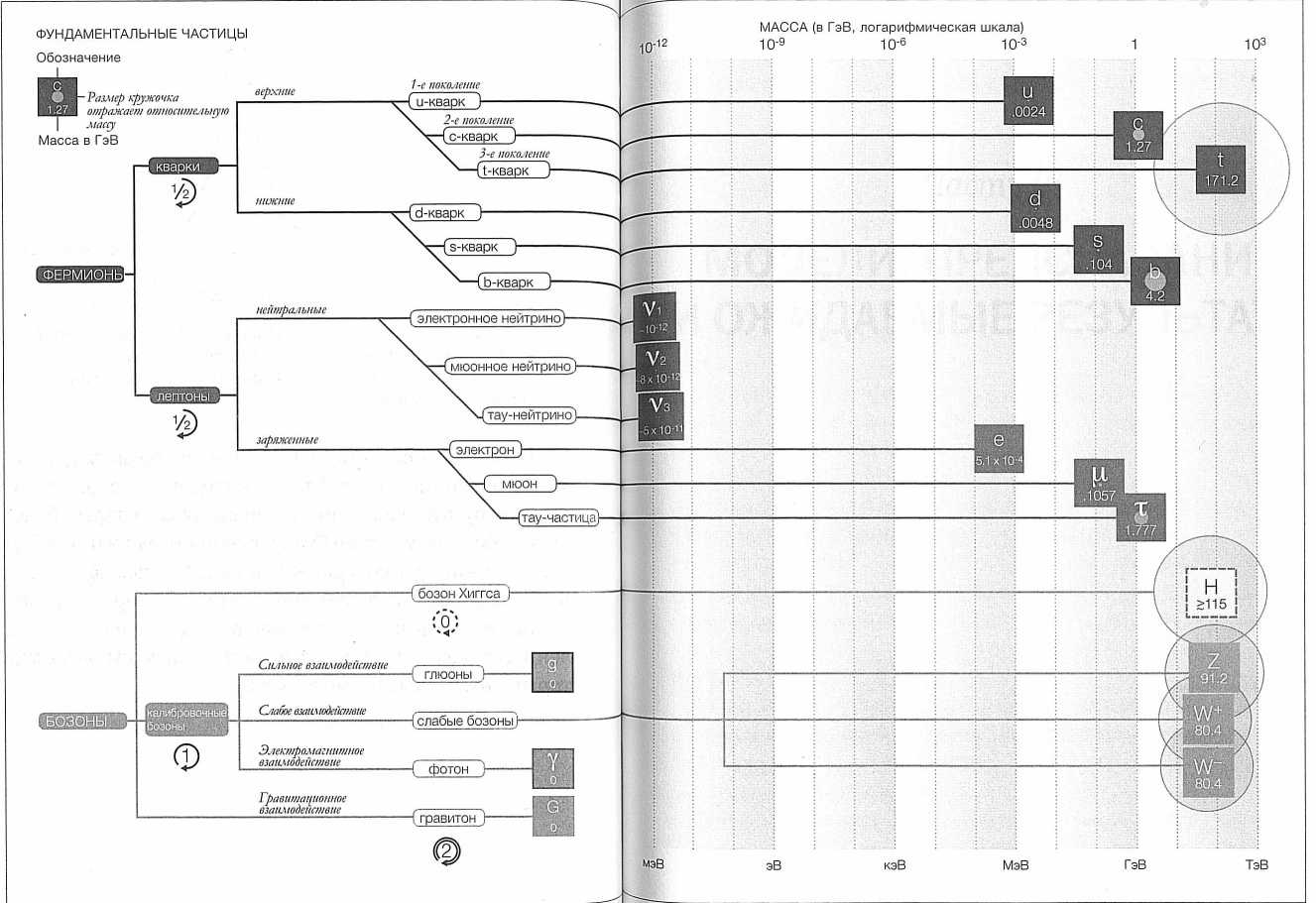
РИС. 46. Частицы Стандартной модели, организованные по типу и массе. В серых кружочках (иногда внутри квадратиков) приведены массы частиц. Число внутри стрелочек, образующих дуги, обозначает величину спина данной частицы. Мы видим здесь загадочное разнообразие элементов Стандартной модели