Книга: Ритм Вселенной. Как из хаоса возникает порядок

* * *

Программа исследований Уинфри, изложенная в этом письме в столь характерном для Уинфри стиле, касалась того, о чем другие исследователи в то время даже не помышляли. Разумеется, он совершенно не вписывался в мейнстрим «нормальной» науки с ее тенденцией к узкой специализации и акцентом на редукционизм, то есть сведение явлений высшего порядка к явлениям низшего порядка; другими словами, Уинфри не думал лишь о генах, или кварках, или нейронных каналах. Более того, он не зацикливался даже на революции, порожденной теорией хаоса, которая, по мнению всех его аспирантов, была на тот момент передовым краем науки, хотя на самом деле эта отрасль науки к тому времени уже достигла своей зрелости и была готова уступить пальму первенства очередной великой тенденции: изучению нелинейных систем, состоящих из огромного множества элементов. Это движение, впоследствии получившее название «теории сложности», следовало представлять себе как естественное ответвление теории хаоса, в каком-то смысле ее оборотную сторону. Вместо того чтобы сосредоточиться на странном и «сумасбродном» поведении малых систем, специалисты по теории сложности были увлечены организованным поведением больших систем. Одна из самых ранних работ Уинфри по самопроизвольной синхронизации биологических осцилляторов уже касалась этой темы. К описываемому мною времени она уже достигла стадии зрелости, причем ее созревание происходило разными путями.

Например, в своем письме он упоминал о том, что собирается работать над «трехмерными скрученными + заузленными волнами». Ключевое слово здесь – трехмерные. Никто прежде не занимался изучением поведения самоподдерживающихся осцилляторов, взаимодействующих в трехмерном пространстве. Как было показано выше, когда теоретики впервые приступили к анализу динамики популяций осцилляторов, они полностью игнорировали пространство, полностью сосредоточившись лишь на времени, на синхронности ритмов, безотносительно взаимного расположения этих осцилляторов. Открытия, которые совершили Винер, Курамото, Пескин и даже сам Уинфри, ограничивались простейшим из возможных случаев, соединением по принципу «каждый с каждым», когда каждый осциллятор оказывает совершенно одинаковое влияние на все остальные осцилляторы. Такая глобальная связь всегда рассматривалась лишь как целесообразный первый шаг – она была кратчайшим путем сквозь джунгли многоосцилляторной динамики. Не было никакой нужды задумываться о пространственной структуре, поскольку каждый осциллятор является соседом всех остальных осцилляторов. После рассмотрения этого простейшего случая можно было ступить на следующую ступеньку теоретической лестницы и рассмотреть осцилляторы, упорядоченные в виде одномерной цепи или кольца. Можно было ожидать, что в этом случае произойдет что-то новое, что-то помимо чистого синхронизма: волны действия могли устойчиво распространяться от одного осциллятора к следующему. Вообще говоря, в осцилляторных моделях с локальными связями более типичным явлением оказывались волны, а не синхронизм. Интуиция, основанная на опыте футбольного болельщика, подсказывает мне следующую аналогию: «запустить волну» и поддерживать ее движение на огромном стадионе бывает гораздо легче, чем заставить всех присутствующих на стадионе одновременно вставать и садиться. Когда кое-кто из математиков попытался подняться по теоретической лестнице еще выше, к двумерным листам осцилляторов, у них попросту закружилась голова: анализ таких систем осложнился до предела. Поэтому когда Уинфри решил продолжить восхождение по этой лестнице и выйти на уровень трехмерных систем, желающих составить ему компанию не нашлось.

Подобные вопросы возникают, конечно же, потому что большинство реальных осцилляторов соединены между собой локально, а не глобально. Кишечник представляет собой длинную трубку осциллирующих нервных и мышечных клеток, разделенную на ритмично сокращающиеся кольца, однако порядок этих сокращений таков, что волны пищеварения движутся в нужном направлении, от желудка к анусу[203]. Каждое кольцо осцилляторной ткани соединено электрически с его ближайшими соседями по обе стороны, превращая кишечник, по сути, в одномерную цепочку осцилляторов. Желудок несколько напоминает двумерную сумку нейро-мышечных осцилляторов в том смысле, что его клетки ритмично перемешивают содержимое желудка и взаимодействуют главным образом со своими соседями на поверхности стенок желудка[204]. А сердце представляет собой толстую, трехмерную совокупность задающих осцилляторных клеток (ритмоводителей в синусно-предсердном узле и их подчиненных) и «возбудимых» клеток, которые подчиняются командам задающих осцилляторных клеток[205]; в случае их запуска с помощью достаточно сильного электрического воздействия они однократно «срабатывают» и возвращаются в состояние покоя, ожидая следующего импульса для запуска. Когда сердце функционирует нормально, такой задатчик ритма генерирует волну электрического возбуждения, которая распространяется вдоль специализированных проводящих волокон к насосным камерам (желудочкам сердца), заставляя их сжиматься и качать кровь к остальным частям тела.

Однако в патологических случаях возбудимые клетки могут взбунтоваться и создать свою собственную волну, вращающийся электрический торнадо, который парирует сигналы, поступающие от задатчика ритма. Кардиологам уже давно известно о том, что такие «вращающиеся потенциалы действия», или «круговые волны возбуждения»[206], могут приводить к тахикардии (повышенная частота сердцебиения), а затем вырождаться в летальную аритмию, называемую вентрикулярной фибрилляцией, когда сердечная мышца беспомощно корчится, дергается и дрожит, отказываясь качать кровь[207]. Ежегодно сотни тысяч здоровых на первый взгляд людей – людей, которые никогда прежде не жаловались на проблемы с сердцем – внезапно умирают[208], когда их сердце переходит в этот разрушительный режим функционирования. Когда Уинфри упомянул в своем письме о «приложениях (по совместительству) к сердечной мышце», он имел в виду именно эти странные электрические торнадо. Он хотел выяснить причины их начала, картину их поведения и возможные способы их предотвращения. Он надеялся, что после того как удастся выяснить причины возникновения этих электрических торнадо и картину их поведения, появится возможность сконструировать дефибрилляторы, действующие на сердце более мягко, чем нынешние грубые устройства, которые сжигают сердце для того, чтобы спасти его.

В 1981 г. нелинейная динамика не достигла того уровня, на котором она могла бы предсказывать поведение таких вращающихся волн в трех измерениях. Не было никакой надежды на то, чтобы просчитать их эволюцию во времени, их удары, их вихревые картины электрической турбулентности. Даже если бы соответствующие вычисления были возможны (например, с помощью какого-нибудь суперкомпьютера), любая такая попытка оказалась бы преждевременной, поскольку никто не знал бы, как интерпретировать полученные результаты. Вообще говоря, никто даже не знал, как могла бы выглядеть фотография одного из этих призрачных злодеев. (Во всяком случае, никому из кардиологов не удавалось наблюдать их воочию.) Поэтому Уинфри считал, что первым делом нужно научиться распознавать их, предсказывать, хотя бы умозрительно, их особенности; в дальнейшем можно будет заняться разгадкой их «модус операнди» (или, образно выражаясь, способа совершения преступления).

Для изучения форм в трех измерениях требовался более примитивный математический аппарат, учитывающий лишь пространство, но не принимающий во внимание время. Упомянув в своем письме о «топологических загадках», Уинфри имел в виду отрасль математики, называемую топологией и занимающуюся изучением непрерывной формы, своего рода обобщенную геометрию, в которой жесткость заменена эластичностью, как если бы все было изготовлено из резины. Формы могут непрерывно деформироваться, сгибаться или скручиваться – но ни в коем случае не разрезаться. Квадрат топологически эквивалентен окружности, поскольку вы можете скруглить его углы. С другой стороны, окружность отличается от формы цифры «8», поскольку вы не можете избавиться от точки пересечения, не прибегнув к помощи ножниц. В этом смысле топология идеально подходит для сортировки форм на обширные классы, основываясь исключительно на их топологических свойствах. План Уинфри заключался в использовании топологии для классификации видов волн, которые могут встретиться в трехмерных полях возбудимых клеток. Зная все возможные варианты, он понимал бы, что именно нужно искать в последующих экспериментах; таким образом, у него появилась бы надежда распознать то, что в противном случае казалось бы просто причудливыми непонятными структурами.

Когда в один из душных июньских дней 1982 г. я прибыл в лабораторию Уинфри, я застал его погрузившимся в ворох бумаг; он сидел на скамье, его рубашка была широко распахнута (очевидно, таким способом он пытался спастись от удушающей жары). Я был несколько смущен столь «неформальным» видом этого великого ученого – я добирался из Коннектикута в Индиану на автомобиле вместе со своим отцом, который никогда ранее не видел моего нового кумира, – но Уинфри обезоружил нас своим искренним дружелюбием. Вскоре отец уехал, и мы с Уинфри остались наедине в лаборатории, которая была уставлена разнокалиберными мензурками, бунзеновскими горелками и прочими приспособлениями, назначение которых я пока не понимал. (Между прочим, на столах я заметил множество лезвий для безопасной бритвы. Как оказалось впоследствии, эти лезвия были любимым инструментом Уинфри, когда ему нужно было что-нибудь разрезать или отрезать. Он с довольным видом вскрикивал «Вжжжик!» каждый раз, когда использовал одно из таких лезвий, чтобы отрезать кусок провода или микропористой фильтровальной бумаги.)

В лаборатории было тихо. Я не заметил там ни одного аспиранта или младшего научного сотрудника. Впрочем, я был готов к этому: в одном из первых писем ко мне, после того как я спросил у Уинфри, кто еще будет работать с нами, он ответил: «Сейчас я мог бы сочинить историю о других аспирантах + сотрудниках. Но, по правде говоря, у меня нет ни тех, ни других. Возможно, дело в том, что я плохо схожусь с людьми, возможно, от меня неприятно пахнет, не знаю… но плотность населения в моей лаборатории = 1. Вы станете единичным событием в жизни моей лаборатории. Не подрывает ли этот факт Ваше доверие ко мне?»

На совместную работу нам было отведено лишь три месяца. Поэтому мне нужно было как можно быстрее входить в курс дела. Уинфри полагал, что мне следует «немного замарать руки», то есть на какое-то время отставить в сторону математику и компьютеры. Моим первым проектом был эксперимент с материалом, кототорый сам Уинфри называл «супом Жаботинского»[209]: химическая реакция, которая поддерживает волны возбуждения, чрезвычайно похожие на электрические волны, которые запускают сердцебиение. Однако в этом эксперименте все должно было оказаться значительно проще, чем с реальным сердцебиением, во всяком случае я не собирался экспериментировать с настоящим сердцем, с его мышцами и сокращениями. Речь шла о неком идеализированном объекте для исследования распространения волн возбуждения в его самой «чистой» форме. В этом смысле эксперименты с пресловутым супом Жаботинского играют такую же роль в исследовании волн сердца, какую играют мушки-дрозофилы в генетике: удобный для изучения упрощенный вариант, в котором заключена сущность более сложных явлений.

Обычно самым занимательным результатом, которого можно ожидать при выполнении какого-либо химического эксперимента, является возникновение облачка дыма или отвратительного запаха. В отличие от этих, вообще говоря, тривиальных случаев, эксперимент с супом Жаботинского позволяет исследователю удовлетворять свое интеллектуальное любопытство в течение очень долгого времени. Если этот суп приготовить в соответствии с оригинальным рецептом, то он ведет себя подобно самопроизвольному осциллятору и является химическим аналогом клеток задатчика сердечного ритма. Он ритмично изменяет свой цвет десятки раз, туда и обратно, становясь попеременно то небесно-голубым, то ржаво-красным, приходя в конце концов (примерно через час после начала химической реакции) в состояние равновесия. На молекулярном уровне такие проявления могли бы выглядеть еще более впечатляюще, если бы, конечно, мы могли наблюдать их: триллионы связанных осцилляторов, пританцовывающих в идеальном синхронизме – самый массовый танец в стиле кантри из тех, которые когда-либо удавалось организовать.

При использовании нового, более утонченного рецепта эта химическая реакция является возбудимой. Поначалу она выглядит обескураживающе инертной. Осцилляции практически отсутствуют. Но если налить тонкий слой этого красного супа в чашку Петри, а затем проколоть этот слой серебряной проволочкой или горячей иголкой, он внезапно запускает голубую круговую волну, которая распространяется, подобно огню на сухой траве. Это химическая волна: импульс запускает реакцию, при которой вещество в чашке Петри окисляется. После того как эта волна пройдет, вещество переходит в состояние покоя и снова приобретает красный цвет, точно так же как трава, выгоревшая в результате пожара, со временем снова начинает расти. (Конечно же, предложенная мною аналогия с травой не идеальна. Химические вещества восстанавливаются гораздо быстрее, чем выгоревшая трава; следом за первой волной может двигаться вторая волна.)

Химические волны совершенно не похожи на волны, изучаемые в традиционных курсах физики (например, звуковые волны или рябь на поверхности пруда). Когда химическая волна распространяется путем диффузии, поверхность жидкости не поднимается и не опускается. Она остается неподвижной. Подвижной оказывается картина возбуждения, своего рода «химическое заражение». Еще одно отличие от обычных волн заключается в том, что химические волны не ослабевают, подобно звуковым волнам или ряби на поверхности пруда, по мере распространения в стороны от места их зарождения. Каждый клочок этой среды служит новым источником энергии, которая подпитывает волну, не давая ей угаснуть.

Допустим теперь, что вы создадите две химические волны в двух разных точках чашки Петри. Голубые круги начнут шириться и приближаться друг к другу. Когда они столкнутся, они не начнут проникать друг в друга или складываться между собой: они взаимно уничтожатся. Это произойдет в силу той же самой причины, по которой горение сухой травы прекращается в результате запуска встречного огня: два пожара – один естественный, а другой искусственный – взаимно уничтожаются, поскольку по обе стороны огня не остается ничего, кроме золы, которая не может гореть. В использованной мною метафоре зола соответствует области истощения, «мертвой» зоне, образующейся позади волны. Химической среде требуется какое-то время для восстановления, прежде чем она снова сможет стать возбужденной.

Во многих отношениях эта химическая среда ведет себя подобно сексуальной реакции человека. Сексуальное возбуждение и возвращение к норме зависят от свойств нервной ткани, которая, подобно супу Жаботинского, принадлежит к общему классу систем, называемых возбудимыми средами. Нейрон может пребывать в трех состояниях: покой, возбуждение и резистентность (абсолютная невозбудимость).

Обычно нейрон пребывает в покое. При недостаточно сильном воздействии он демонстрирует слабую реакцию и возвращается в состояние покоя. Но при достаточно сильном воздействии нейрон возбуждается и приводится в действие. Затем нейрон становится резистентным (в течение какого-то времени его невозможно возбудить) и наконец возвращается в состояние покоя. Параллели с химическими волнами распространяются на потенциалы действия – электрические волны, которые движутся вдоль нервных аксонов. Они также перемещаются, не ослабляясь, а когда две такие волны сталкиваются между собой, они взаимно уничтожаются. Вообще говоря, все эти утверждения относятся в равной мере к электрическим волнам в другой возбудимой среде – сердце. В этом и заключается прелесть данной абстракции: качественные свойства одной возбудимой среды распространяются на все возбудимые среды. Все эти возбудимые среды можно изучать одним махом. Родственная схожесть между супом Жаботинского, нервной тканью и сердечной мышцей сохраняется вплоть до структуры математических уравнений, которые управляют их нелинейной динамикой, – весьма глубокая аналогия.

Однако суп Жаботинского обеспечивает ряд преимуществ, особенно важных для начинающего экспериментатора. Не требуется приносить в жертву животных. Не приходится иметь дело с анатомическими сложностями, наподобие запутанного клубка нейронных сетей или архитектуры сердечной мышцы со скрученными волокнами. Самое главное – эти волны можно наблюдать невооруженным глазом, причем движутся они довольно медленно, а потому отпадает необходимость использования сложного записывающего оборудования. Напротив, визуализация волн на сердце сопряжена с колоссальными техническими проблемами (по крайней мере на сегодняшний день) даже для лабораторий, располагающих внушительным бюджетом, поскольку для этого требуются потенциалочувствительные красители, многоэлектродные системы и прочие новейшие технологии.

С помощью супа Жаботинского ученые начали раскрывать тайны распространения волн в возбудимых средах. В частности, именно с помощью супа Жаботинского удалось открыть новый вид волн – вращающуюся самоподдерживающуюся волну, имеющую форму спирали. Хотя ее геометрия выглядит весьма элегантно, ее последствия носят деструктивный характер. Вращающиеся спиральные волны на сердце – это причина тахикардии и, в самом плохом случае, вентрикулярной фибрилляции, сопровождаемой внезапной смертью от сердечного приступа.

Открытие супа Жаботинского и его впечатляющих спиральных волн – это история догмы, разочарования и окончательного обоснования[210]. Разумеется, термин «суп Жаботинского» – это название, которым предпочитал пользоваться сам Уинфри. В наши дни суп Жаботинского называют «BZ-реакцией» в честь Белоусова и Жаботинского, российских ученых, которые, соответственно, изобрели и усовершенствовали его.

В начале 1950-х годов Борис Белоусов пытался воссоздать в пробирке модель цикла Кребса – метаболический процесс, который происходит в живых клетках. Когда он смешал лимонную кислоту и ионы бромата в растворе серной кислоты (в присутствии цериевого катализатора), он, к немалому своему удивлению, наблюдал, как эта смесь сначала пожелтела, затем, примерно через минуту, стала бесцветной, затем, еще через минуту, снова стала желтой, затем снова бесцветной и т. д. Эти осцилляции повторились несколько десятков раз, пока наконец (примерно через час) не было достигнуто состояние равновесия.

Сегодня уже никого не удивляет тот факт, что химические реакции могут самопроизвольно осциллировать; такие реакции стали стандартной демонстрацией на лекциях по химии. Но во времена, когда Белоусов сделал свое открытие, самопроизвольная осцилляция химических реакций оказалась такой неожиданностью, что в ее возможность отказывались верить. В то время считалось, что, вследствие действия законов термодинамики, все растворы химических реагентов должны монотонно продвигаться к состоянию равновесия. Научные журналы один за другим отмахивались от статьи Белоусова. В письме с отказом опубликовать статью Белоусова один из редакторов даже не удержался от ехидного высказывания в адрес автора, который «вполне возможно, открыл открытие».

Удрученный таким отношением к своему открытию, Белоусов решил никогда не упоминать о нем в разговорах со своими коллегами. Все же он опубликовал краткое резюме своей статьи в материалах одной из медицинских конференций Советского Союза. Впрочем, поначалу никто в научном мире не обратил внимания на эту публикацию. Тем не менее в конце 1950-х годов слухи о его открытии упорно циркулировали среди московских химиков, а в 1961 г. научный руководитель аспиранта, которого звали Анатолий Жаботинский, посоветовал ему ознакомиться с этой статьей. Жаботинский подтвердил, что в эксперименте, поставленном Белоусовым, нет никакой ошибки и что дело обстоит именно так, как изложено в резюме к его статье. Более того, Жаботинский ознакомил с работой Белоусова участников международной конференции, состоявшейся в Праге в 1968 г. и оказавшейся одной из тех редких возможностей, когда западные и советские ученые имели шанс непосредственно пообщаться друг с другом. В то время ученые проявляли повышенный интерес к биологическим и биохимическим осцилляциям, а BZ-реакция рассматривалась как весьма перспективная модель для изучения более сложных систем.

Аналогия с биологией оказалась на удивление тесной. В начале 1970 г. Альберт Николаевич Заикин и Жаботинский обнаружили распространяющиеся волны возбуждения в тонких, невзболтанных слоях BZ-реакции. Эти волны напоминали концентрические окружности; при столкновении такие волны взаимно гасились, водобно электрическим волнам в нейронной или сердечной ткани. Казалось даже, что они возникают из чего-то похожего на задатчики ритма, разбросанные в произвольном порядке точки, которые самопроизвольно порождали волны.

Изучив эту работу, Уинфри отправил Жаботинскому (с которым он познакомился на пражской конференции двумя годами ранее) письмо, чтобы выяснить, встречались ли ему какие-либо другие картины волн, помимо концентрических колец. В своих собственных лабораторных экспериментах с некоторыми видами плесени Уинфри наблюдал спиральные волны[211], но это была гораздо более сложная система, состоящая из живых организмов, которым были присущи циркадные циклы. Уинфри хотел выяснить, наблюдались ли спирали в гораздо более простой химической системе Жаботинского. Он сомневался в этом, исходя из ряда математических соображений; он полагал, что мог бы доказать, что волны должны иметь форму именно замкнутых колец. Однако ответа от Жаботинского ждать пришлось очень долго. Почта из Советского Союза, особенно переписка между учеными, в то время шла очень долго (наверное, службы безопасности с обеих сторон усердно занимались перлюстрацией). Вынужденная приостановка работы выводила Уинфри из терпения. Он самостоятельно состряпал какое-то подобие рецепта, которым пользовались Заикин и Жаботинский, и рецепт, придуманный Уинфри, оказался удачным: спирали появлялись повсюду. Уинфри не знал об этом, но Жаботинский тоже наблюдал эти волны в 1970 г. при подготовке своей диссертации, а Валентин Кринский из г. Пушкино полагал, что такие волны должны возникать в любой возбудимой среде, в том числе и в сердечной мышце. В настоящее время является общепризнанным фактом то, что спиральные волны присущи всем химическим, биологическим и физическим возбудимым средам.

Борису Белоусову было бы, наверное, приятно осознавать, что он является первооткрывателем столь важного феномена.

В 1980 г. он, Жаботинский и трое других ученых стали лауреатами Ленинской премии, высшей государственной награды в Советском Союзе, за их открытия, связанные с осциллирующими реакциями. Впрочем, для Бориса Белоусова это оказалось слабым утешением – он умер десятью годами ранее.

Самым удивительным в спиральных волнах является то, что они кажутся живыми. Это самоподдерживающееся явление. Они не нуждаются в задатчиках ритма: спиральная волна является своим собственным задатчиком ритма. Если вы наблюдаете спиральную волну в тонком слое возбудимой BZ-реакции, она похожа на непрерывное завихрение, гоняющееся за своим собственным хвостом и беспрестанно регенерирующее себя.

Вообще говоря, ее вращение является второстепенным делом. Более существенным для нас является то, что она распространяется в направлении, перпендикулярном себе в каждой точке вдоль фронта волны. В связи с этим возникает путаница, обусловленная спецификой геометрии спирали: распространение спиральной волны выглядит как вращение. (Вспомните оптическую иллюзию, наблюдаемую на вращающихся столбах с нанесенной на них винтовой линией, которые устанавливали в прежние времена возле парикмахерских. Если смотреть на винтовую линию, нанесенную на такой вращающийся столб, то кажется, будто она движется вверх. Разумеется, никакого такого движения нет, просто эта винтовая линия вращается вместе со столбом. В этом случае вращение создает впечатление движения вверх. Примерно с такой же оптической иллюзией мы сталкиваемся, когда наблюдаем за спиральными волнами.)

Тем не менее в каком-то смысле вращение спиральной волны является реальным. Каждая точка в окружающей среде периодически осциллирует: она повторно возбуждается каждый раз, когда через нее проходит волна. Таким образом, каждая точка в чашке Петри проходит циклически через знакомые нам стадии возбуждения, резистентности и покоя, а затем повторного возбуждения. Новым здесь является то, что спиральная волна создала осцилляцию, которая структурирована в пространстве, а также во времени. Вместо жесткой синхронизации – пространственной однородности, которую наблюдал Белоусов в самых ранних своих экспериментах, когда вся мензурка изменила свой цвет одномоментно – осцилляция теперь похожа на «волну», запускаемую на трибунах стадиона болельщиками во время футбольного матча и циркулирующую по трибунам в результате того, что люди встают и садятся в нужные моменты времени.

Рассмотрим еще более тесную аналогию. Вообразите кольцо, составленное на полу из тысячи костяшек домино. Допустим, что мы решили воспользоваться услугами проворного помощника, который берется быстро восстанавливать каждую из костяшек сразу же после того, как она упадет. Мы ударяем первую костяшку, и волна падений начинает быстро распространяться по кольцу костяшек. Наш помощник четко отслеживает распространение этой волны, с трудом успевая восстанавливать на прежнем месте каждую из упавших костяшек. В данном случае удар по костяшке соответствует возбужденному состоянию, упавшая костяшка соответствует состоянию резистентности, а восстановленная костяшка соответствует состоянию покоя. Такая волна будет циркулировать до бесконечности – или до тех пор, пока наш помощник не свалится с ног от изнеможения.

Биологическая версия того же самого эксперимента была выполнена физиологом А. Г. Майером в 1906 г. с помощью медузы[212]. Он соорудил кольцо нейромышечной ткани из обода зонтикообразного купола медузы, а затем воздействовал импульсом электрического тока на одну точку этого кольца, заранее позаботившись о том, чтобы волна распространялась по кольцу только в одном направлении. Нейроимпульс циркулировал по кольцу в течение шести суток, совершив при этом около полумиллиона циклов.

Таким образом, должно быть ясно, что волны могут очень долго циркулировать по одномерным контурам возбудимых сред. Однако при попытке перенести те же идеи на два измерения (важный случай спиральных волн) возникают определенные проблемы. В приведенном выше обсуждении молчаливо предполагалось, что к моменту возвращения волны среда успевает восстановиться из своего периода резистентности. Это вполне допустимое предположение, если контур достаточно велик или если скорость волны не очень высока. Но вблизи центра спиральной волны это предположение не соблюдается: контур, по которому прошло возбуждение, становится слишком маленьким.

В конечном счете ядро спирали не осциллирует подобно остальной части этой среды. Мы не видим на нем ритмических изменений цвета, оно не демонстрирует пиков и падений интенсивности свечения или каких-либо других признаков осцилляции. Амплитуда цикла падает до нуля. Такая точка называется сингулярностью фазы, что означает, что здесь невозможно точно определить фазу окружающей осцилляции. Фаза становится неоднозначной. Эта загадочная ситуация аналогична тому, что происходит на Северном и Южном полюсах. В таких сингулярных точках на поверхности нашей планеты сходятся все временные пояса, а цикл дня и ночи распадается. Солнце никогда не поднимается и не садится: оно просто кружит над горизонтом. На Северном и Южном полюсах вопрос «который час?» лишен всякого смысла. Вы можете жить здесь по любому времени – или вообще вне времени.

Но для спиральной волны сингулярность фазы – это нечто большее, чем точка на нашей планете, где нога человека ступает лишь в очень редких случаях. Для спиральной волны сингулярность фазы – это двигатель, который приводит волну в действие. Поразительно, но пока это ядро остается в неприкосновенности, спиральная волна в целом может регенерировать себя независимо от того, каким повреждениям подверглись ее наружные витки. К тому же спиральные волны нелегко уничтожить еще по одной причине: они испускают волны почти с такой же скоростью, какую допускает соответствующая среда. Поэтому они способны «парировать» другие входящие волны, например концентрические окружности, запускаемые удаленными задатчиками ритма. Эти вторгающиеся волны уничтожаются при столкновениях со спиральными витками. Они не могут продвинуться дальше. Напротив, более быстрые спиральные волны неумолимо надвигаются на более медленные задатчики ритма, захватывая их территорию и постепенно уничтожая их. Именно поэтому на достаточно продолжительном отрезке времени картина BZ-реакции всегда становится похожа на рисунок «пейсли»[213], заполненный спиралями, причем круговые волны вообще не видны. Спирали способна противостоять только другая спираль.

Здесь мы наблюдаем случай самопроизвольного порядка в его чистом и простом виде. Начинаем с «супа» химических веществ, который обладает свойством возбудимости. Затем прикасаемся к нему серебряной проволочкой и шлепаем этой проволочкой по поверхности «супа», чтобы создать таким образом произвольный рисунок возбуждения. Нет никакой структуры, совершеннейший беспорядок, но все же из этого беспорядка возникает рисунок «пейсли». Между тем во всем, что происходит, нет ничего мистического. Такой рисунок является результатом действия законов возбудимой среды, а эти законы, в свою очередь, являются следствием нелинейной динамики.

Поэкспериментировав в лаборатории Уинфри с супом Жаботинского в течение нескольких дней, я смог собрать основные факты, касающиеся спиральных волн. Затем Уинфри поставил передо мной следующую задачу: попытаться воспроизвести эксперимент, касающийся нового вида спиральной волны[214], сообщение о котором недавно появилось в журнале Nature. После пары недель неудач Уинфри стало понятно, что экспериментатор из меня никудышный. Разумеется, для меня это не было новостью; чтобы стать хорошим экспериментатором, требуются годы упорного труда.

К счастью, главная цель Уинфри на те летние месяцы заключалась совсем в другом. Как он упоминал в письме ко мне, он намеревался работать над «загадками, касающимися трехмерных скрученных + заузленных волн в “супе Жаботинского”». Вопрос заключался в следующем: что представляют собой трехмерные обобщения спиральных волн? Как они выглядят? Можем ли мы визуализировать их каким-либо способом? Какие математические законы управляют их допустимыми формами?

К тому времени у Уинфри уже был создан неплохой задел. Вскоре после открытия им в 1970 г. двумерных спиральных волн он размышлял над тем, что может произойти, если взять тонкий слой BZ-реакции, содержащий плоскую спираль, а затем постепенно утолщать этот слой. Подобно барельефу, эта спираль постепенно приобретала бы третье измерение. В результате такого процесса формировалась бы поверхность, похожая на свиток.

Между тем сингулярная точка в ядре постепенно удлинялась бы, превращаясь в нить на краю свитка. И точно так же, как спиральная волна вращается вокруг своего ядра, свиткообразная волна[215] должна вращаться вокруг своей нити.

Вращающаяся свиткообразная волна… До того времени наука не знала ничего подобного. Подходящие аналогии найти было нелегко. Свиткообразная волна – это химический торнадо. Одно существенное различие: жидкость остается неподвижной. Перемещается лишь волна химической активности, трехмерный водоворот расширящегося возбуждения. Кроме того, торнадо тянется от облаков до поверхности земли, а где заканчиваются свиткообразные волны? Уинфри убедил себя, что они не могут просто остановиться в каком-то определенном месте в середине жидкости. Они либо затухали бы на границе (то есть на стенках мензурки или вверху, на границе «воздух-жидкость»), либо вообще нигде не заканчивались бы. Иными словами, свиткообразная волна могла бы кусать свой собственный хвост и замыкаться на самой себе. В таком случае она была бы похожа не столько на торнадо, сколько на колечко дыма.

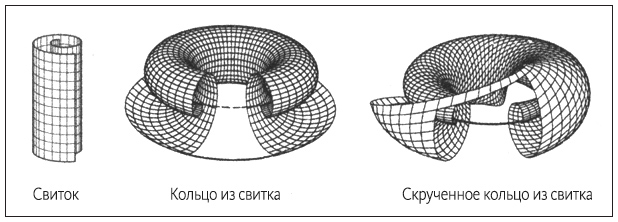
Этот образ пленил Уинфри. Действительно ли существуют такие «кольца из свитка»? В 1973 г. ему удалось доказать, что такие «кольца из свитка» действительно существуют. Поставленный им эксперимент был весьма остроумным. Вместо использование обычной мензурки, заполненной жидкой BZ-реакцией, он приготовил высокую стопку фильтровальной бумаги из пористой нитроцеллюлозы, пропитанной теми же химическими веществами. После создания подходящих условий, которые требовались, по его мнению, для воспроизведения «кольца из свитка», он предоставил возможность реакции начаться, а затем внезапно затормозил ее химическим способом, зафиксировав характерный рисунок «кольца из свитка» в состоянии приостановленной анимации. Пытаясь проанализировать полученный образец, он разделил эту стопку фильтровальной бумаги на тонкие слои, подобно экспериментатору, подготавливающему для исследования под микроскопом срезы какого-нибудь экзотического организма, а затем реконструировал его, срез за срезом, на листах неотражающего стекла. Образец оказался именно таким, как ожидалось: волна в форме бублика с поперечным сечением в виде спирали.

Но Уинфри хотел понять, существуют ли другие виды «колец из свитка»[216]. Возможно ли скручивание свиткообразных волн на целое число оборотов, прежде чем они замкнутся сами на себя? Пояс можно скрутить таким способом; почему же это невозможно в случае «колец из свитка»? Или их можно завязывать в узлы? Можно ли связывать между собой кольца друг через друга, подобно браслетам или кольчуге? Изучая весь этот спектр бесконечного множества «колец из свитка», связанных между собой, скрученных и соединенных с помощью узлов самыми разнообразными способами, Уинфри вскоре обнаружил, что один из гипотетических элементов этого множества находится под запретом.

Используя одну из теорем топологии, Уинфри доказал невозможность скрученного кольца из свитка, по крайней мере в виде отдельно взятого объекта. Его структура заключала в себе внутреннее противоречие. Если бы такое кольцо было скрученным, оно автоматически должно было бы переплетаться с какой-то другой сингулярной нитью, а это означало бы, что исходное кольцо не было одиночным. Эта топологическая теорема указала на существование второго свитка, непредвиденного, но обязательно связанного посредством первого. В результате дальнейшего анализа Уинфри смог показать, что, хотя отдельно взятое скрученное кольцо из свитка существовать не может, существованию взаимно связанной пары ничто не препятствует. Такая структура представлялась идеально жизнеспособной.

Из этого следовал весьма впечатляющий вывод: геометрия «колец из свитка» была вполне законной. Некоторые конфигурации были допустимыми, тогда как другие – нет. Соответствующие правила еще предстояло выяснить.

Делом первостепенной важности было представить, как выглядят скрученные кольца из свитка. Абстрактная топологическая аргументация Уинфри предполагала, что скрученное кольцо из свитка должно быть переплетено с какой-то другой сингулярной нитью, но ни Уинфри, ни я не могли представить, как складывается воедино такая структура в целом: скрученный свиток плюс дополнительная сингулярность переплетения. Вообще говоря, когда за несколько лет до описываемого мною времени Уинфри попытался изобразить такую структуру, у него получилась фантастическая картинка в стиле Маурица Корнелиса Эшера[217], представителя так называемого имп-арта, который исследовал пластические аспекты понятий бесконечности и симметрии, а также особенности психологического восприятия сложных трехмерных объектов.

Но теперь все должно было быть по-другому. На дворе был 1982 г., а в нашем распоряжении были компьютеры Apple. Компьютер мог изобразить поверхность за нас; от нас требовалось лишь рассказать ему, что он должен изобразить. Моя задача заключалась в том, чтобы написать компьютерную программу, которая вычисляла бы эту поверхность что называется «в лоб». Идея была проста: скрученный свиток – это лишь окружность из ребер спирали, каждое из которых слегка повернуто по отношению к своим соседям. Таким образом, я попросил компьютер вычислить некоторую совокупность точек на спирали, затем скопировать и повернуть всю спираль на один шаг по окружности – и одновременно с этим скрутить ее на один шаг. Эту последовательность действий нужно было повторять снова и снова, пока спираль не вернется в свое исходное положение, совершив один полный оборот по окружности и одно полное скручивание. Невыясненным оставался лишь один вопрос: какой должна быть длина каждого ребра спирали? То есть сколько витков должно быть в ней? Ответ в этом случае дает нам химия: спиральная волна движется до тех пор, пока не столкнется с другой спиральной волной. Части столкнувшихся спиралей, оказавшиеся за этой границей, нужно стереть, поскольку они взаимно уничтожили друг друга (подобно тому, что происходит со столкнувшимися волнами в возбудимой среде).

Как и требовалось, Apple II распечатал таблицу с несколькими сотнями чисел, представляющих точки на поверхности скрученного свитка. Теперь все, что нам оставалось сделать, это ввести полученные таким образом числа в графическую программу, результаты работы которой раскроют наконец загадку скрученного свитка. Я запустил на выполнение графическую программу Bill Budge 3D Graphics System, приобретенную Уинфри, и мы, затаив дыхание, стали ждать завершения ее работы. Хм-м-м… Картинка получилась слишком грубой: количества заданных мною точек оказалось явно недостаточным. К сожалению, программа Bill Budge 3D Graphics System оказалась не в состоянии обработать большее количество точек – она с огромным трудом справилась даже с тем, которое я ей задал. Итак, наши надежды на компьютер не вполне оправдались, поэтому нам пришлось достраивать поверхность от руки. Мы распечатали грубую картинку, полученную с помощью Bill Budge 3D Graphics System, и, вооружившись цветными карандашами, начали «украшать» распечатку, надеясь увидеть нечто более вразумительное. Увы! Мы поняли, что с разгадкой придется подождать.

Тем временем мы с Уинфри приступили к рассмотрению более теоретических вопросов, пытаясь найти правила для топологии свиткообразной волны. Не имея четкого представления о том, в каком именно направлении следует двигаться, мы решили положиться на интуицию. В лаборатории Уинфри хранились изрядные запасы красного и зеленого стоматологического воска, а также оранжевой формовочной глины и превеликое множество ершиков для прочистки трубок. Все это были совершенно необходимые вещи для изготовления моделей узлов, связей и скрученных поверхностей.

Наша работа была организована следующим образом. Пока я сидел за компьютером или за рабочим столом в лаборатории, вылепливая те или иные фигуры из стоматологического воска и пытаясь визуализировать невиданные ранее формы, Уинфри пытался изображать картины свиткообразной волны в блокноте для рисования. Особено понравившиеся ему варианты он вырезал с помощью лезвия для безопасной бритвы (не забывая при этом вскрикнуть «Вжжжик!») и вклеивал их в лабораторный журнал. Шел час за часом. Время от времени один из нас, когда ему в голову приходила интересная мысль, нарушал молчание. После этого мы пытались совместно обсудить эту мысль, прояснить ее и проверить ее рациональность, каждый раз с трудом подбирая нужные слова, поскольку трехмерная геометрия – вообще говоря, весьма труднопередаваемая и неуловимая материя. Но в конечном счете нам всегда удавалось понять друг друга, после чего мы пытались совместными усилиями втиснуть эти новые идеи в рамки какой-то теории. Эти математические обсуждения были весьма бурными, но доброжелательными. Мне вообще казалось, что у меня появился еще один мозг – правда, гораздо лучший, чем мой первый мозг. Так проходили дни, один за другим. Обычно мы обедали вместе, а в солнечные дни мы предпочитали сидеть у фонтана возле его дома: он делал наброски в своем блокноте, а я рисовал разные варианты поверхности в своем воображении. К десяти часам вечера у кого-нибудь из нас начинала раскалываться голова, после чего мы расставались до следующего утра.

К августу мы выяснили правила для всех возможных конфигураций связанных и скрученных колец. С узлами возникли проблемы[218]. Нам не удалось выяснить ни одного правила относительно узлов. Поэтому мы решили начать с простейшего случая: отдельно взятого кольца из свитка, в котором завязан узел в виде трилистника. (Чтобы завязать узел в виде трилистника, возьмите шнурок для ботинок, завяжите на нем узел «клеверный лист», как если бы вы завязывали узел на шнурках своих ботинок, а затем соедините вместе концы шнурка. Результирующая кривая представляет собой петлю с узлом, которая напоминает своим видом клевер-трехлистник.)

Нас интересовало, имеет ли какой-либо математический и химический смысл кольцо из свитка в форме трилистника. А если бы такое кольцо в действительности присутствовало в мензурке BZ-реакции, то должно ли оно всегда быть связано с другими кольцами или оно может существовать само по себе? А если да, то какой должна быть надлежащая степень скручивания? И как должны были бы выглядеть волны, исходящие от него?

Чтобы сделать эти абстракции более осязаемыми, я скатал из стоматологического воска длинные шнуры, а затем согнул их и слепил их концы между собой таким образом, чтобы получилось некое подобие трилистника. Полученная геометрическая фигура должна была представлять собою сингулярную нить – источник и внутренний край свиткообразной волны. Затем мне предстояло изготовить восковую модель самой поверхности свиткообразной волны. Если сингулярная нить похожа на длинный тонкий деревянный штырь свитка, то сама волна похожа на пергамент, который раскручивается с этого штыря. Она представляет собой поверхность, которая начинается и заканчивается на таких штырях, в то же время плотно наворачиваясь на них. К счастью, это наворачивание было для нас в математическом смысле несущественно: от него всегда можно было избавиться, туго растянув свиткообразную волну (представьте, что волна изготовлена из эластичной ткани). Принципиально важным для нас в свиткообразной волне было то, что она начинается и заканчивается на нити. Других границ у такой поверхности нет. Воспользовавшись воском другого цвета, я приступил к конструированию поверхности волны, кусок за куском, каждый раз начиная вдоль нити и продвигаясь дальше, пока все такие куски не сложились в один сплошной лист.

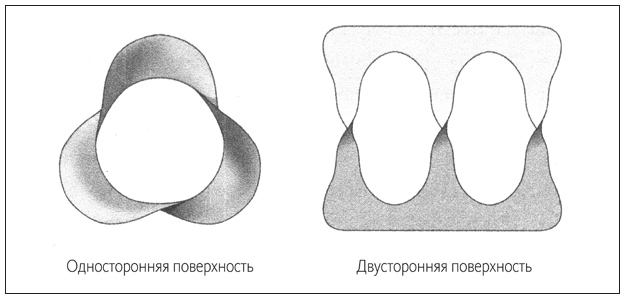
После этого нужно было уяснить, сколько сторон у такого листа: одна или две? На первый взгляд, этот вопрос звучит странно: разве бывают односторонние поверхности? Самым знаменитым примером является так называемый лист (лента, петля) Мебиуса: полоска бумаги, скрученная на полоборота и замкнутая в виде кольца. Если провести пальцем по поверхности такого контура, начиная с любой его точки, то в конце концов ваш палец вернется в ту же точку – но на другой стороне бумаги (правда, такое утверждение было бы неправильным, поскольку никакой «другой» стороны нет: передняя и задняя стороны являются одним и тем же). В этом смысле у листа Мебиуса есть только одна сторона.

Если бы мои восковые поверхности представляли собой нечто подобное, это было бы плохо. С точки зрения химических законов, свиткообразная волна должна представлять собой двустороннюю поверхность из-за непреложного факта, касающегося возбудимой среды: волны распространяются перпендикулярно самим себе, вторгаясь на неактивные территории и оставляя позади себя резистентную «выжженную пустыню». Это означает, что у такой волны есть передняя и задняя сторона, тогда как у листа Мебиуса есть только одна сторона. Это можно сформулировать по-другому. Представьте, что вы закрасили одну сторону листа Мебиуса красным цветом (сторону, которая движется вперед), а другую его сторону вы закрасили черным цветом (сторону, за которой остается «выжженная пустыня»). Но то и другое является одной и той же стороной, и в конце концов вам придется красить черным цветом поверх красного. Все концепция распространения волны вперед утрачивает смысл, если волна оказывается односторонней.

Трилистник можно изображать разными способами. Интересно отметить, что некоторые из них ведут к односторонним поверхностям (и, следовательно, неприемлемы), тогда как другие дают желаемые двусторонние поверхности, то есть являются подходящими кандидатами на форму волнового фронта. Поэкспериментировав еще немного, я пришел к выводу, что все приемлемые поверхности топологически эквивалентны, то есть обладают подходящим изгибом и растяжением, причем каждую из них можно непрерывно деформировать, превращая в любую другую. Таким образом, существовал лишь один правильный ответ, и этот ответ уже был известен нам. Вот как должна была выглядеть поверхность свиткообразной волны для трилистника.

Нам предстояло ответить на следующий вопрос: должен ли результирующий свиток быть скрученным, и если да, то в какой степени. Чтобы измерить это скручивание экспериментальным путем, я укладывал кусок нити вдоль поверхности из воска так, чтобы он всегда пролегал параллельно ее наружному краю, оказываясь лишь на миллиметр внутри ее, и продолжал укладывать эту нить вдоль всей поверхности, пока она не соединялась со своим началом, то есть пока не замкнется контур. Этот контур также образовывал трилистный узел – в точности такой, как первоначальная нить, а вместе они определяли два края воображаемой ленты.

Эта лента напоминала мне что-то из моей дипломной работы в колледже, в которой рассматривалась топология сверхспиральных молекул ДНК. Ключевой концепцией в том случае была математическая величина, называемая числом зацеплений в двухцепочечной сверхспиральной ДНК[219], которая, грубо говоря, показывает, сколько раз одна нить ДНК обвивается вокруг другой нити ДНК, помимо обвивания, предполагаемого самой двойной спиралью. Эта величина зависит как от скручивания в ДНК, так и от ее трехмерного пути в пространстве. Теперь, в случае свиткообразной волны, число зацеплений ленты должно заключать в себе всю важную информацию о скручивании волны, а также о форме ее заузленной нити. Когда я вычислил число зацеплений, оказалось, что оно равняется нулю. Замечательно! Все оказалось так просто. Свиткообразные волны в форме трилистника могут существовать, а число зацеплений у них всегда равняется нулю. Позже нам удалось доказать, что то же самое должно быть справедливо для любого узла, а не только для трилистного узла.

По окончании лета я перебрался в Бостон, чтобы поступить в магистратуру в Гарвардском университете. Впрочем, я продолжал поддерживать контакты с Уинфри. Нам предстояло написать несколько статей; к тому же нам нужно было найти ответы на две давние загадки. Зимой того же года я навестил Уинфри в доме его родителей, в городке Лонгбоут-Ки, Флорида, где нам наконец-то удалось решить проблему топологии свиткообразной волны в ее наиболее общей форме. Нам удалось доказать, что произвольное количество колец из свитка могут быть разнообразными способами связаны, скручены и заузлены между собой при условии, что они удовлетворяют единственному уравнению: число зацеплений ленты каждого кольца плюс все его взаимные связи с другими кольцами должно в сумме равняться нулю. В противном случае соответствующая структура оказывалась недопустимой. С некоторой долей иронии мы называли это принципом исключения[220], по аналогии с принципом исключения Паули в химии, который ограничивает атомную структуру элементов и дает начало картинам, которые мы наблюдаем в периодической таблице элементов. Для нас «элементами» были разрешенные конфигурации колец из свитка и узлов, расположенные в порядке возрастания сложности. «Водородом» было для нас отдельно взятое кольцо из свитка, в котором не было ни узлов, ни скручиваний. «Гелием» было два кольца, связанные друг с другом и скрученные однократно.

Спустя несколько месяцев мы провели лето в Лос-Аламосской национальной лаборатории, работая на самом быстродействующем суперкомпьютере в мире. (Это был Cray-1, но местные творцы атомной бомбы называли его более зловещим именем «X-машина».) С помощью Мела Пруитта, местного специалиста по компьютерной графике, мы наконец-то построили картины скрученного кольца из свитка, которые позволили нам раскрыть секреты неуступчивой сингулярности, которая, как нам было известно на основе абстрактных математических рассуждений, должна проходить через его центр. Увидев эти картины, мы с Уинфри раскрыли рты от удивления. Это было все равно что встретить давнего друга по переписке из какой-то другой страны, которого мы никогда не видели, но образ которого пытались нарисовать в своем воображении.

На протяжении двадцати лет, которые прошли с того времени, в научном мире отмечался всплеск интереса к спиральным и свиткообразным волнам. За это время химики выполнили с помощью компьютерной видеозаписи гораздо более тщательные измерения BZ-реакции и обнаружили, что спирали не всегда вращаются вокруг одной точки – зачастую они отклоняются в стороны[221]. Внутренний кончик спиральной волны может вращаться по кругу, или вырисовывать картины цветков, или даже хаотически блуждать. Математики с жадностью накинулись на эти результаты, объясняя их как нестабильности, являющиеся следствием нелинейной динамики.

Роль Священного Грааля во всем этом продолжает оставаться за сердечными аритмиями[222]. Многие кардиологи и физиологи экспериментальным путем подтвердили, что спиральные и свиткообразные волны могут вызывать тахикардию, хотя путь к вентрикулярной фибрилляции остается противоречивым. Наиболее вероятными подозреваемыми являются блуждающая спиральная волна, разделение одной спирали на несколько и возрастание нестабильности трехмерной свиткообразной волны. Несколько групп кардиологов и математиков упорно работают над решением этой проблемы, и истинный виновник этих опасных недугов вскоре может быть выявлен.

В течение всего этого времени Уинфри неустанно занимался свиткообразными волнами и пытался выяснить их возможную роль в возникновении сердечных аритмий. Его воображение по-прежнему будоражили образы узлов и связей; но теперь его в большей степени интересовала динамика узлов и связей, а не их фиксированная геометрия, которую мы исследовали вместе. Опираясь на огромную мощь современных суперкомпьютеров, он вместе со своими студентами смоделировал движение связанных и заузленных свиткообразных волн[223]. Их нити неистово болтаются из стороны в сторону и скручиваются между собой, когда волны от части одной нити ударяют друг о друга. Тем не менее, многие из этих структур оказываются на удивление устойчивыми: у них не наблюдается самопроизвольное развязывание. В этом смысле они фундаментальны, подобно элементарным частицам в квантовой физике. Они представляют собой базовые локализованные решения уравнений поля для возбудимой среды[224]. Они должны иметь важное значение для нас. Именно поэтому Уинфри никогда не откажется от их изучения.

Он также пытался найти (но еще не нашел) простой закон, который мог бы объяснить, как именно эти нити плавно скользят и скручиваются. Даже если бы удалось найти элегантный ответ на этот вопрос, никто не знает, имеет ли он какое-то значение для выявления причин аритмии. До сих пор в сердечной мышце удалось обнаружить только самую элементарную из свиткообразных волн: прямой свиток без узлов и связей. Не теряя надежды на получение снимка своих неуловимых частиц, Уинфри вернулся в лабораторию и изобрел новый вид оптической томографии[225] для BZ-реакции. Его работы получили заслуженное признание в научном мире: в 1984 г. он получил премию Фонда Макартура, присуждаемую за гениальные научные открытия; в 1989 г. – премию по кардиологии Einthoven Award; а в 2000 г. – премию имени Норберта Винера по прикладной математике. Его сын Эрик – компьютерный вундеркинд подросткового возраста во времена, когда я познакомился с ним – также недавно получил премию Фонда Макартура (между прочим, они стали первой в истории парой «отец и сын», ставшей лауреатами этой престижной премии). Что же касается вклада Уинфри в изучение связанных осцилляторов и синхронизма, то именно он продемонстрировал нам чудеса, которые случаются, когда осцилляторам предоставляется возможность свободно взаимодействовать между собой в пространстве; именно он показал нам, как они самоорганизуются вокруг точек, в которых отсутствует время, продуцируя спирали в двух измерениях и свиткообразные волны в трех измерениях. В предстоящие годы ученые приступят к изучению еще более общей формы соединения, когда осцилляторы оказываются связаны не только со своими соседями в обычном пространстве, но и со своими соседями в одном загадочном и мощном виде сети – виде, который соединяет всех нас лишь шестью степенями связности.